Why 4x8 and 6x8 Are, Perhaps Surprisingly, Some of the Hardest Multiplication Facts for Students to Remember
There's a cognitive principle behind this: associative interference, the phenomenon that conceptually related pieces of knowledge can interfere with each other's recall.
Cross-posted from here.
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.
Let’s do a little experiment. I want you to take a guess at the top 4 multiplication facts (within $10 \times 10$) that students have the most trouble remembering.
Most people know that higher-number facts are typically harder than lower-number facts, but the 10s are really easy and the 9s follow a pattern that makes them fairly easy as well.
So, we arrive at the following guess: $8 \times 8$ is probably the hardest, then $7 \times 8,$ then $7 \times 7,$ tied with $6 \times 8.$ Or something like that.
This is a decent guess. These are all some of the hardest facts.
But when you look at the results, such as here, you maybe surprised by the following two observations:
- $6 \times 8$ is the hardest
- $4 \times 8$ is at least as hard as $7 \times 7$
So, what gives?
There’s actually a cognitive principle behind this: associative interference, the phenomenon that conceptually related pieces of knowledge can interfere with each other’s recall.
For instance, when recalling $4 \times 8,$ related facts like $\mathbf{4} \times 6 = \mathbf{24}$ and $3 \times \mathbf{8} = \mathbf{24}$ interfere with the spreading activation during the recall process and increase the likelihood of the error $4 \times 8 = 24.$
("Spreading activation" is a method by which connections between information can be used to recall information in response to a stimulus. The stimulus activates some piece(s) of information, and the activity flows through connections to other pieces of information.)
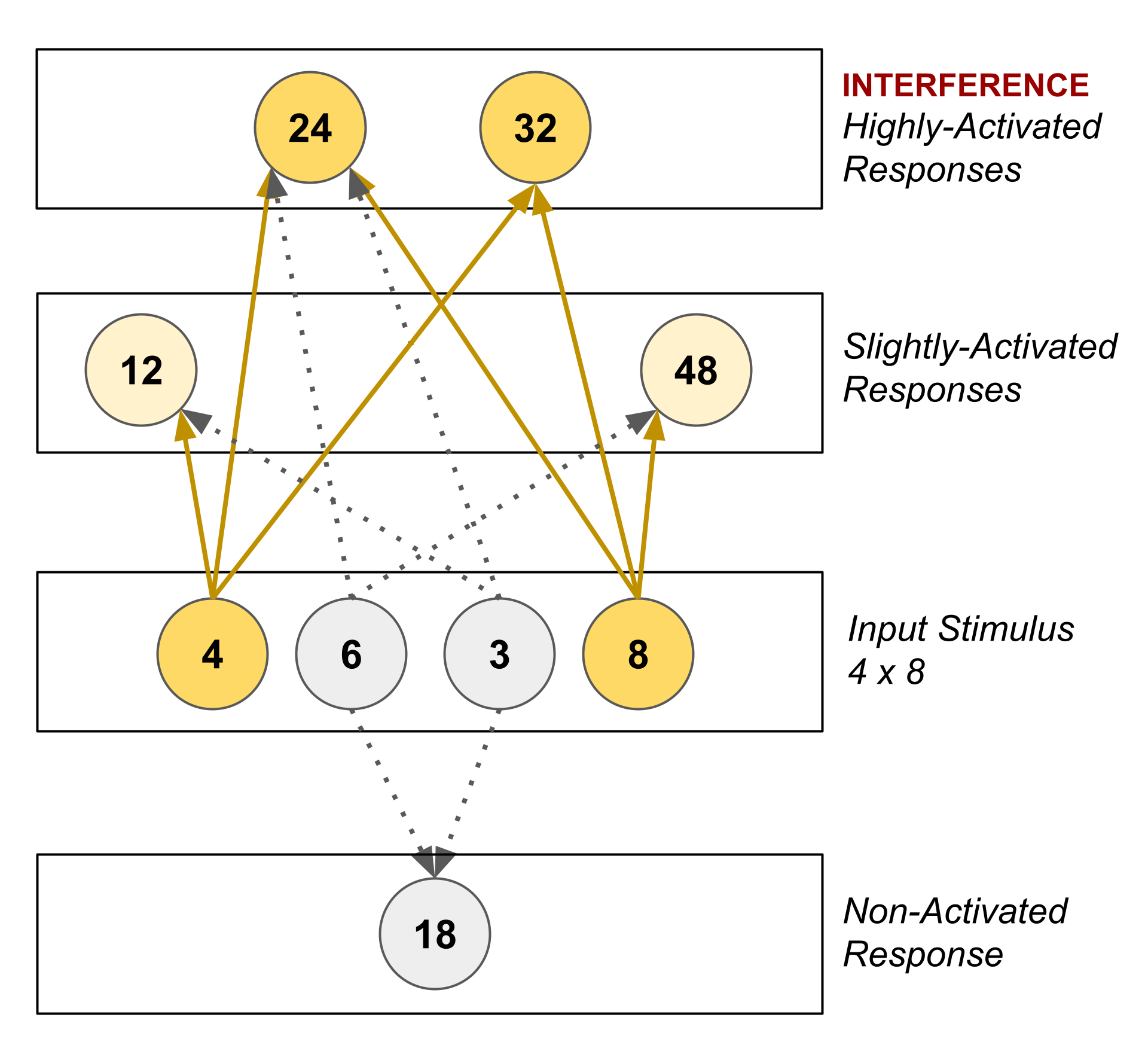
Multiple studies have shown that well over half, and potentially as high as 90%, of multiplication mistakes are caused by interference (see Campbell, 1987 for a summary).
So, what does this mean for pedagogy?
Two things.
1) Don’t introduce interfering topics together. Space them out over time. You want to scaffold the initial learning to reduce the cognitive load (e.g., avoid interference).
2) After the student has learned interfering facts in isolation, start mixing them together to focus on distinguishing between them. This will create more cognitive load, but since the student has already trained and reduced their cognitive load associated with tasks from phase 1, they’ll have more mental bandwidth to handle the extra load.
It’s just like how, if you’re lifting weights at the gym, you start off with something manageable and gradually put weight on the bar over time. (In this analogy, “putting weight on the bar” represents introducing desirable difficulty into the learning process.)
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.