Vertical Asymptotes of Rational Functions

by Justin Skycak (x.com/justinskycak) on May 03, 2018

Vertical asymptotes are vertical lines that a function approaches but never quite reaches.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Vertical Asymptotes of Rational Functions. In Justin Math: Algebra. https://justinmath.com/vertical-asymptotes-of-rational-functions/

Want to get notified about new posts? Join the mailing list.

Unlike polynomials, rational functions can “blow up” to positive or negative infinity even for relatively small input values. Such input values are called vertical asymptotes, because they represent vertical lines that the function approaches but never quite reaches.

Demonstration

For example, consider the rational function $r(x)=\frac{3x+2}{x-5}$. As we input numbers closer and closer to $5$ while staying greater than $5$, the function output blows up to positive infinity.

$\begin{align*} r(5.1) &= \frac{17.3}{0.1} = 173 \\ r(5.01) &= \frac{17.03}{0.01} = 1703 \\ r(5.001) &= \frac{17.003}{0.001} = 17003 \end{align*}$

On the other hand, as we input numbers closer and closer to $5$ while staying less than $5$, the function output blows up to negative infinity.

$\begin{align*} r(4.9) &= \frac{16.7}{-0.1} = -167 \\ r(4.99) &= \frac{16.97}{-0.01} = -1697 \\ r(4.999) &= \frac{16.997}{-0.001} = -16997 \end{align*}$

As a result, we say the function has a vertical asymptote at $x=5$.

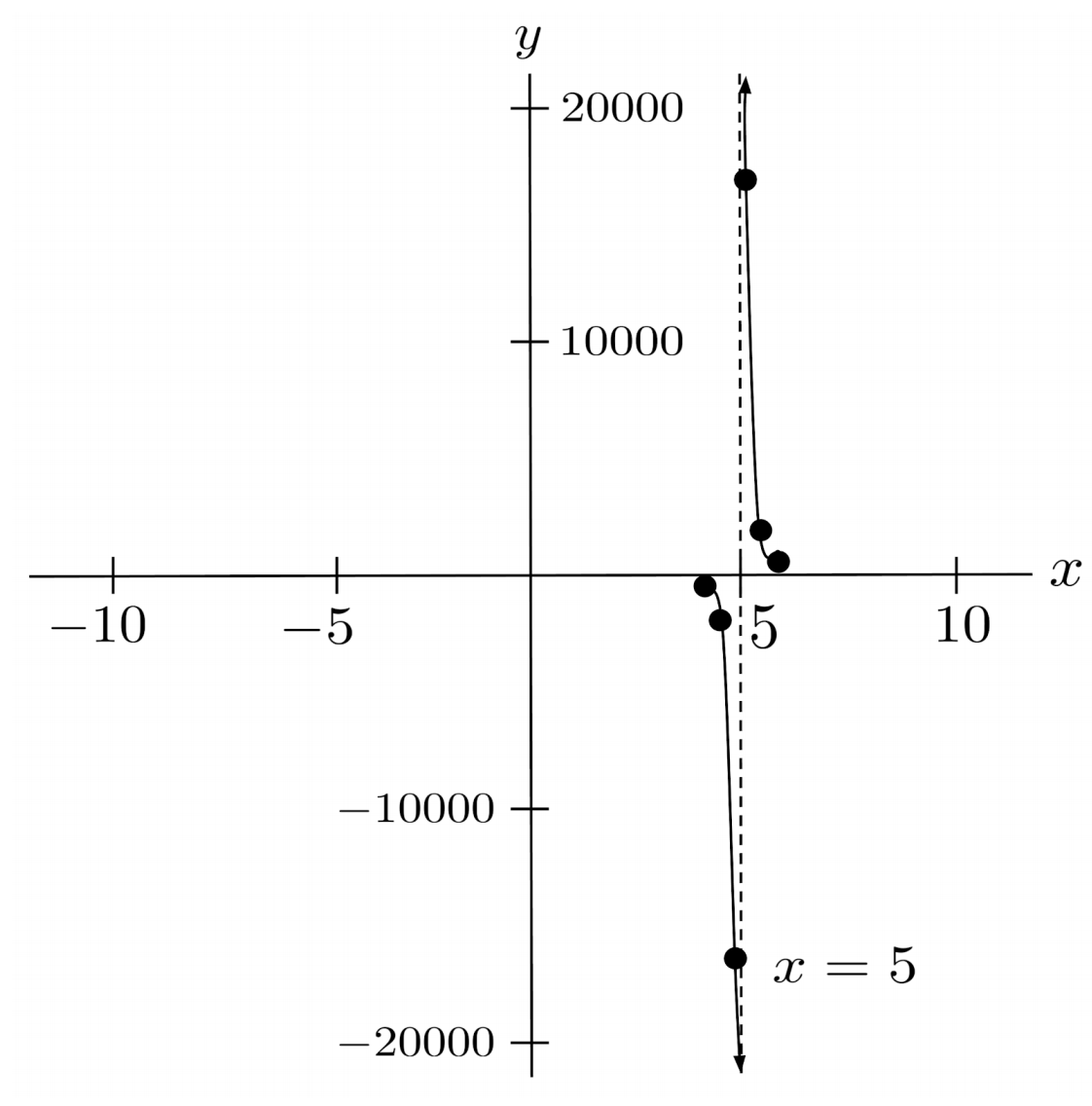
To understand why this happens, notice that as our inputs become closer and closer to $5$, the denominator becomes closer and closer to $0$, while the numerator becomes closer and closer to $17$.

As a result, we end up dividing a fairly constant numerator by a smaller and smaller denominator, which yields a bigger and bigger result.

When the input is greater than $5$, the denominator is positive, which makes the result positive. When the input is less than $5$, the denominator is negative, which makes the result negative.

Case of Multiple Vertical Asymptotes

In general, vertical asymptotes occur when the denominator is zero and the numerator is nonzero. In the above example, when we input $5$, the denominator is $0$, but the numerator is $17$.

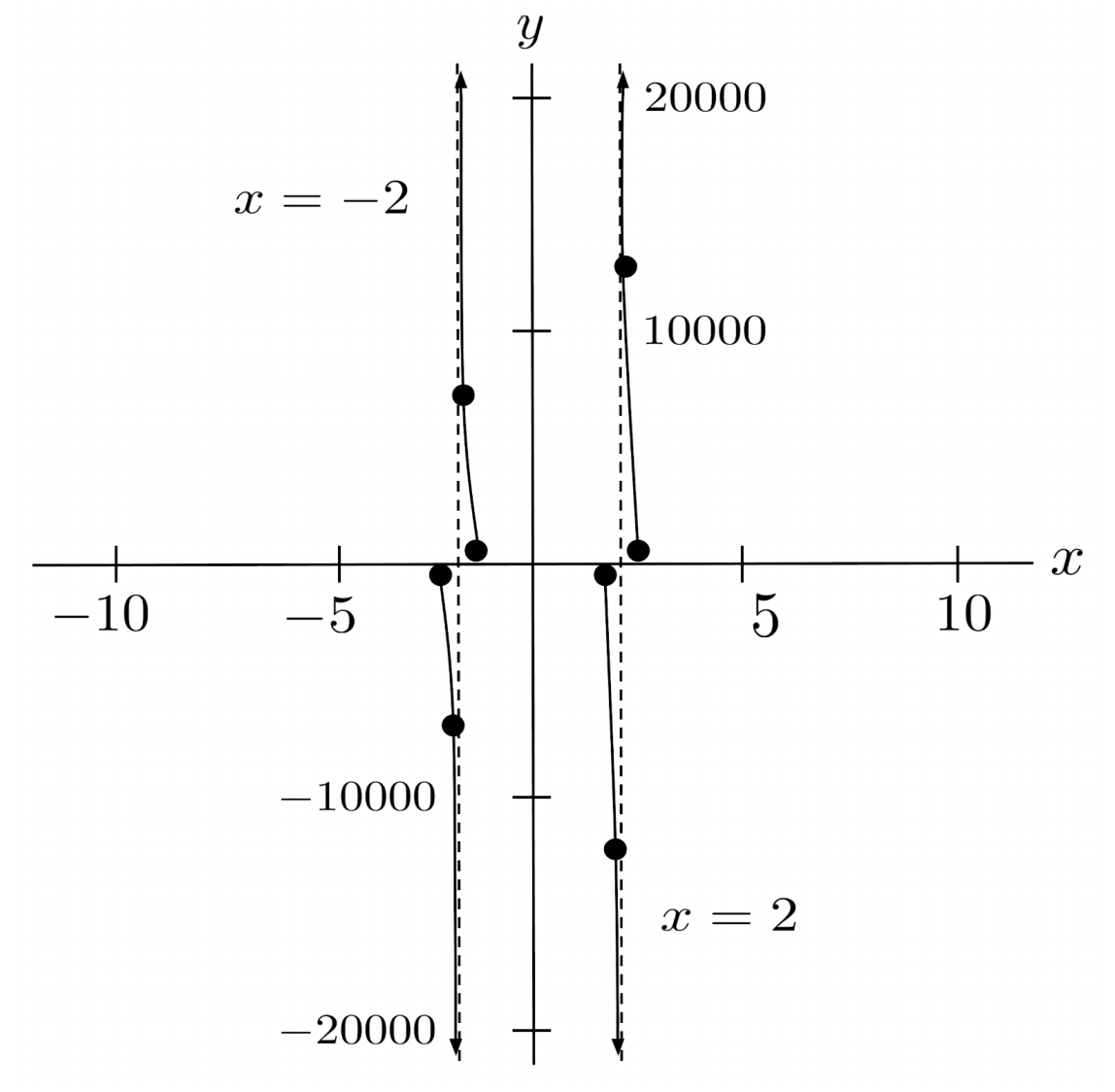
There can also be multiple vertical asymptotes – for example, in the rational function $r(x)=\frac{2x+1}{x^2-4}$, inputting $2$ makes the denominator $0$ while the numerator is $5$, and inputting $-2$ makes the denominator $0$ while the numerator is $-3$.

We confirm that $x=2$ and $x=-2$ are indeed asymptotes by evaluating the function.

$\begin{align*} &r(1.99) \approx -125 \hspace{.5cm} && r(-1.99) \approx 75 \\ &r(1.9999) \approx -12500 && r(-1.9999) \approx 7500 \\ &r(2.01) \approx 125 && r(-2.01) \approx -75 \\ &r(2.0001) \approx 12500 && r(-2.0001) \approx -7500 \end{align*}$

Case of No Vertical Asymptote

On the other hand, if the denominator is zero and the numerator is also zero, then the input is not necessarily a vertical asymptote of the function.

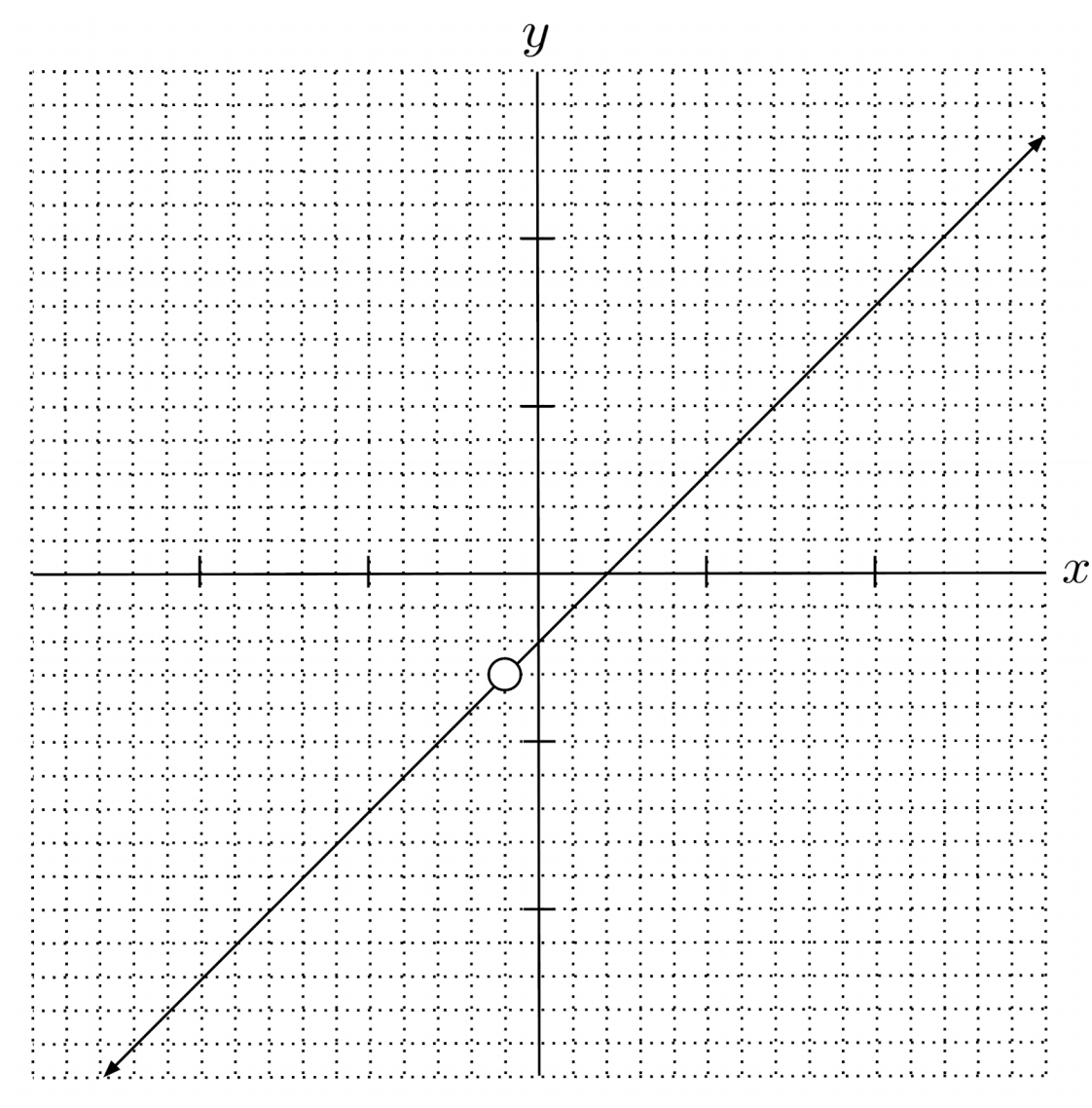
For example, inputting $-1$ to $r(x) = \frac{x^2-x-2}{x+1}$ makes the denominator $0$, but it also makes the numerator $0$, and the result is that the fraction does not blow up to infinity.

$\begin{align*} &r(1.01) = -3.01 \hspace{.5cm} && r(-0.99) = -2.99 \\ &r(1.0001) = -3.0001 && r(-0.9999) = -2.9999 \end{align*}$

To understand this behavior, notice that provided $x$ is not equal to $-1$, the function can simplify.

$\begin{align*} r(x) &= \frac{x^2-x-2}{x+1} \\ &= \frac{(x+1)(x-2)}{x+1} \\ &= x-2 \end{align*}$

When we input an $x$ that is not equal to $1$, the $x+1$ factors in the numerator and denominator cancel each other out, and we are left with $x-2$.

As a result, the graph of $r$ is just the graph of $y=x-2$ with a hole at $x=-1$ (where it is undefined).

Exercises

Find the vertical asymptote(s), if any, of each rational function. (You can view the solution by clicking on the problem.)

$1) \hspace{.5cm} r(x)=\dfrac{2x}{x-4}$

Solution:
$x=4$

$2) \hspace{.5cm} r(x)=\dfrac{x^2-1}{3x+5}$

Solution:
$x=-\frac{5}{3}$

$3) \hspace{.5cm} r(x)=\dfrac{2x^2-8}{x-2}$

Solution:
$\text{none}$

$4) \hspace{.5cm} r(x)=\dfrac{x+3}{x^2+3x+2}$

Solution:
$x=-1,-2$

$5) \hspace{.5cm} r(x)=\dfrac{x^2+x-2}{x^2-x-6}$

Solution:
$x=3$

$6) \hspace{.5cm} r(x)=\dfrac{x^2+2x-15}{(x^2-9)(x^2+x-12)}$

Solution:
$x=-4,-3,3$

$7) \hspace{.5cm} r(x)=\dfrac{x^4-5x^2+1}{x^2-3x+2}$

Solution:
$x=1,2$

$8) \hspace{.5cm} r(x)=\dfrac{x^2+7x+12}{x^3+x^2-16x-16}$

Solution:
$x=-1,4$

$9) \hspace{.5cm} r(x)=\dfrac{x^2-9}{x^3-3x^2+9x-27}$

Solution:
$\text{none}$

$10) \hspace{.5cm} r(x)=\dfrac{2x-3}{(3x-2)(8x^2-2x-3)}$

Solution:
$x=-\frac{1}{2}, \frac{2}{3}, \frac{3}{4}$

Want to get notified about new posts? Join the mailing list.