Thales’ Theorem
Every inscribed triangle whose hypotenuse is a diameter is a right triangle.
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.
Suppose we have a circle, and we draw a diameter across it. If we choose another point on the circle, we can connect it to the ends of the diameter to form a triangle. Depending on how we angle the diameter and choose the off-diameter point, we can form a variety of different triangles.
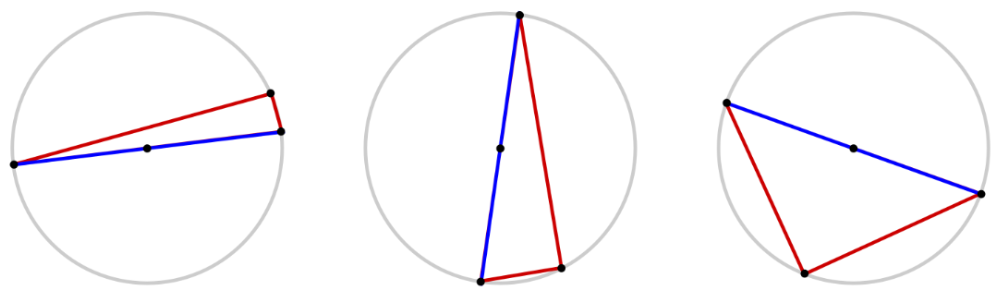
However, all of these different triangles have one thing in common. Can you figure out what it is? Here’s a hint: look at the angle opposite the diameter.
According to Thales’ Theorem, it turns out that any triangle constructed in this way will be a right triangle. No matter how flat or steep we angle the diameter, or how short or long we make the legs of the triangle, the angle across from the diameter will always be a right angle.
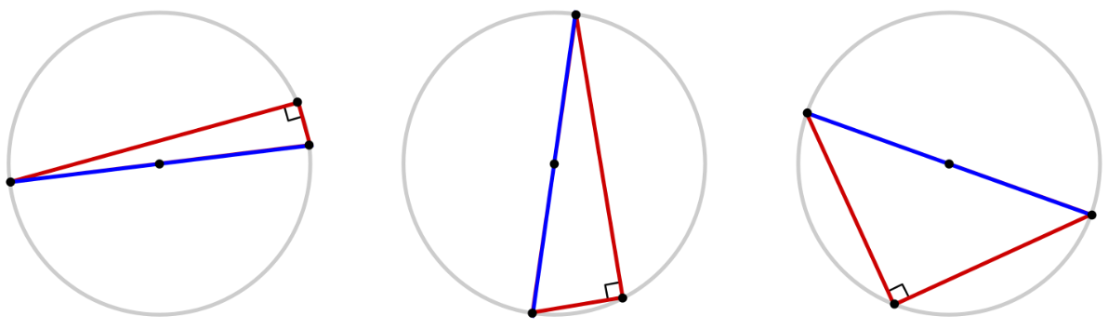
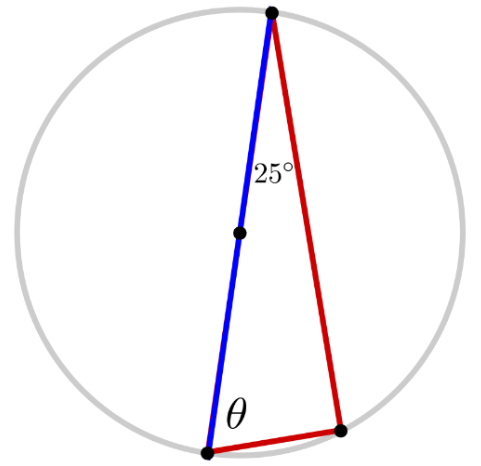
We can use Thales’ Theorem to solve for missing angles in triangles formed by three points on a circle, having one side as a diameter. For example, since Thales’ Theorem tells us that the triangle below is a right triangle, we know that its two acute angles must add up to $90^\circ.$ Solving $25^\circ + \theta = 90^\circ,$ we find that $\theta = 90^\circ - 25^\circ = 65^\circ.$
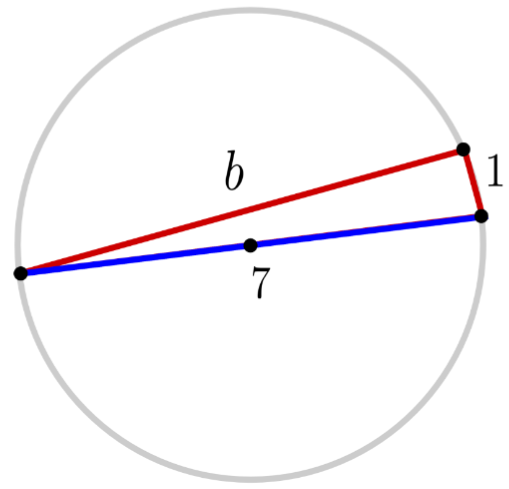
We can also use Thales’ Theorem to solve for missing sides in such triangles. For example, since Thales’ Theorem tells us that the triangle below is a right triangle, its sides must satisfy the Pythagorean theorem $a^2 + b^2 = c^2,$ where $c$ is the hypotenuse (the longest side) of the triangle, and $a$ and $b$ are the two shorter legs of the triangle. Substituting in the side lengths $a=1$ and $c=7,$ we find that $1^2 + b^2 = 7^2,$ which simplifies to $1 + b^2 = 49$ and yields a solution $b = \sqrt{48} = 4 \sqrt{3}.$
To see why Thales’ Theorem is true, first imagine copying each side of the triangle and moving it to the opposite side of the circle, to form a parallelogram. Notice that the other diagonal of the parallelogram is also a diameter of the circle.
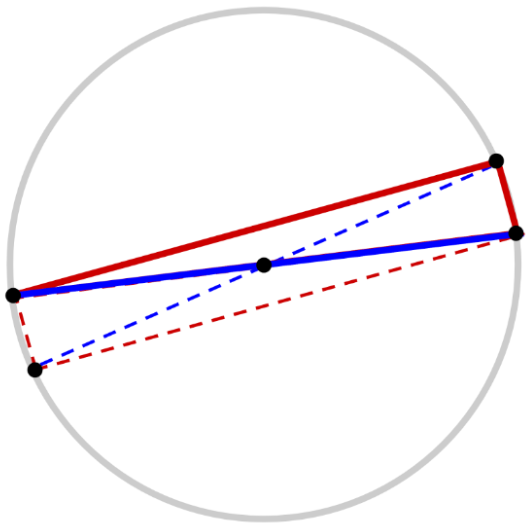
The diagonals of the parallelogram must have the same length, then, since they are both diameters of the circle. And since the diagonals have the same length, the parallelogram must be a rectangle. Finally, since all the angles of the rectangle must be right angles, the triangle must be a right triangle.
Exercises
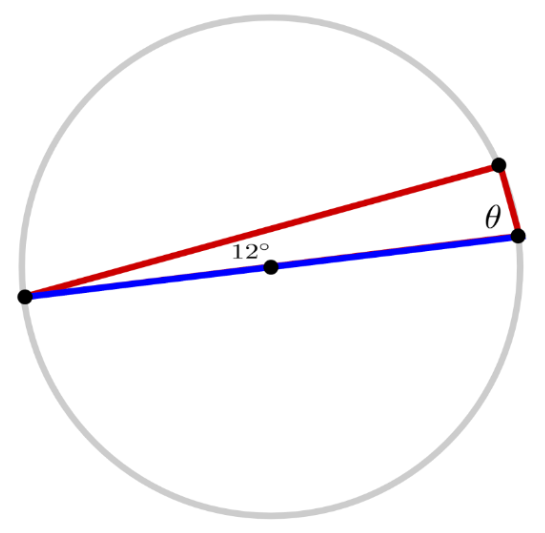
- Find the missing angle measure $\theta$ in the triangle below.
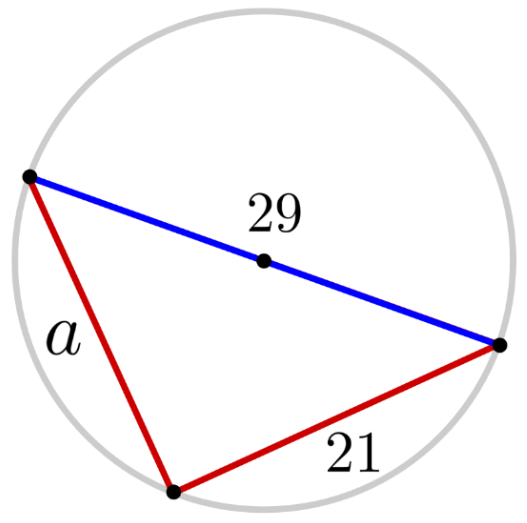
- Find the missing side length $a$ in the triangle below.
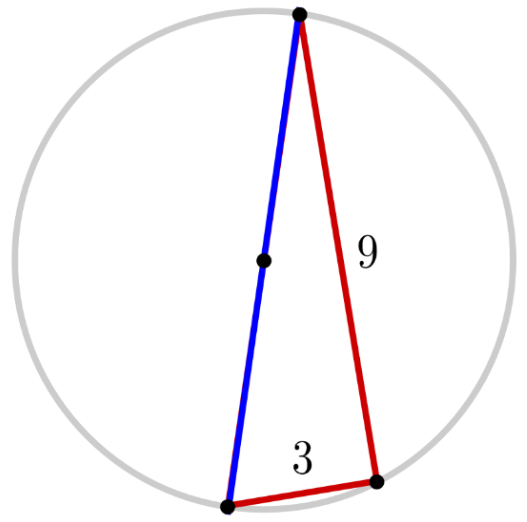
- Find the diameter of the circle below.
Solutions
- $\theta = 78^\circ$
- $a = 20$
- $\textrm{diameter} = 3 \sqrt{10}$
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.