Systems of Inequalities

To solve a system of inequalities, we need to solve each individual inequality and find where all their solutions overlap.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Systems of Inequalities. In Justin Math: Algebra. https://justinmath.com/systems-of-inequalities/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

To solve a system of inequalities, we need to solve each individual inequality and find where all their solutions overlap. For example, to solve the system

we first graph each individual inequality and darken where the shading overlaps.

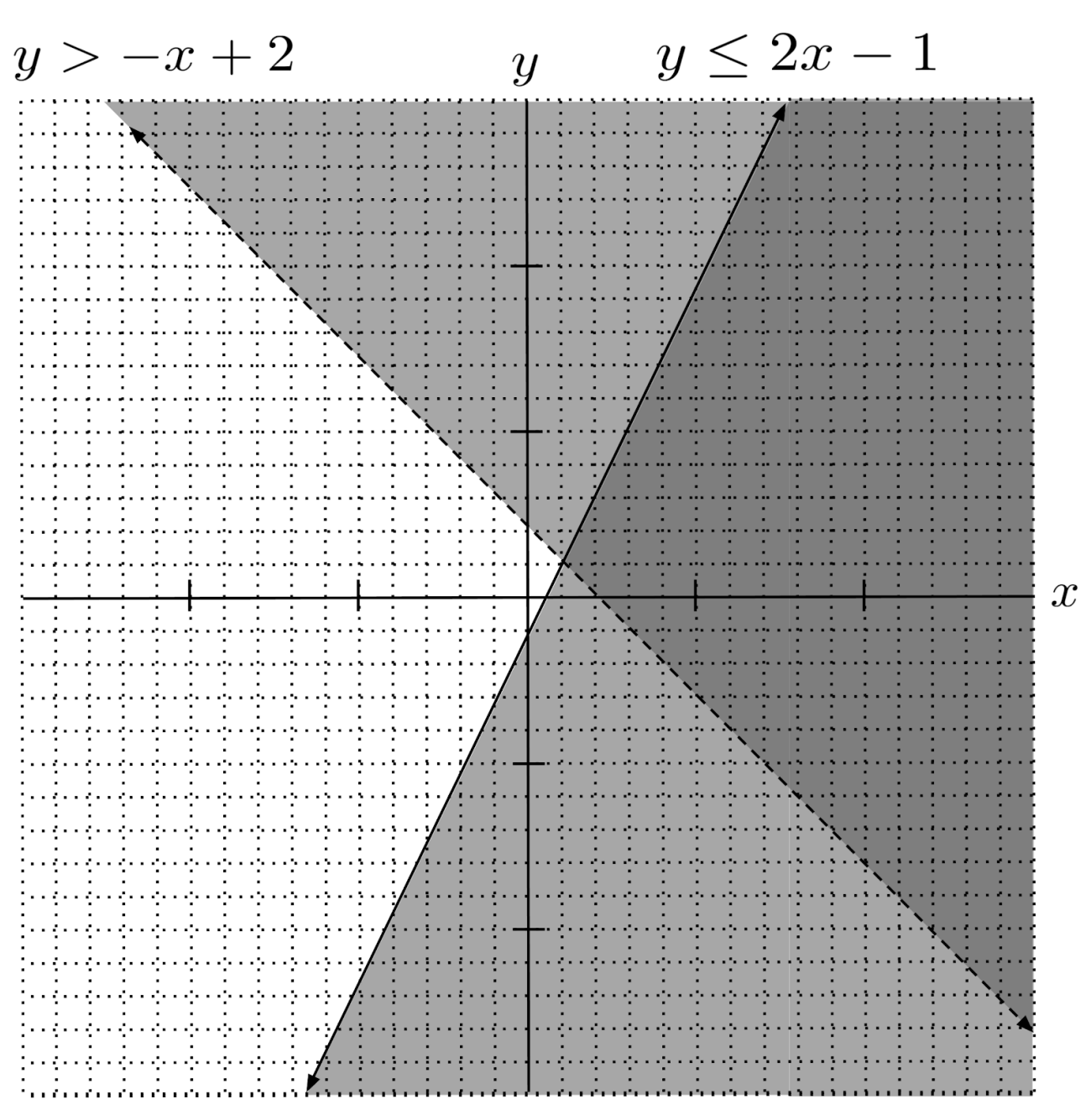
The solution to the system consists of points that satisfy BOTH individual inequalities, so the solution is just the overlap of the two shadings, which appears as the most darkened part of the graph.

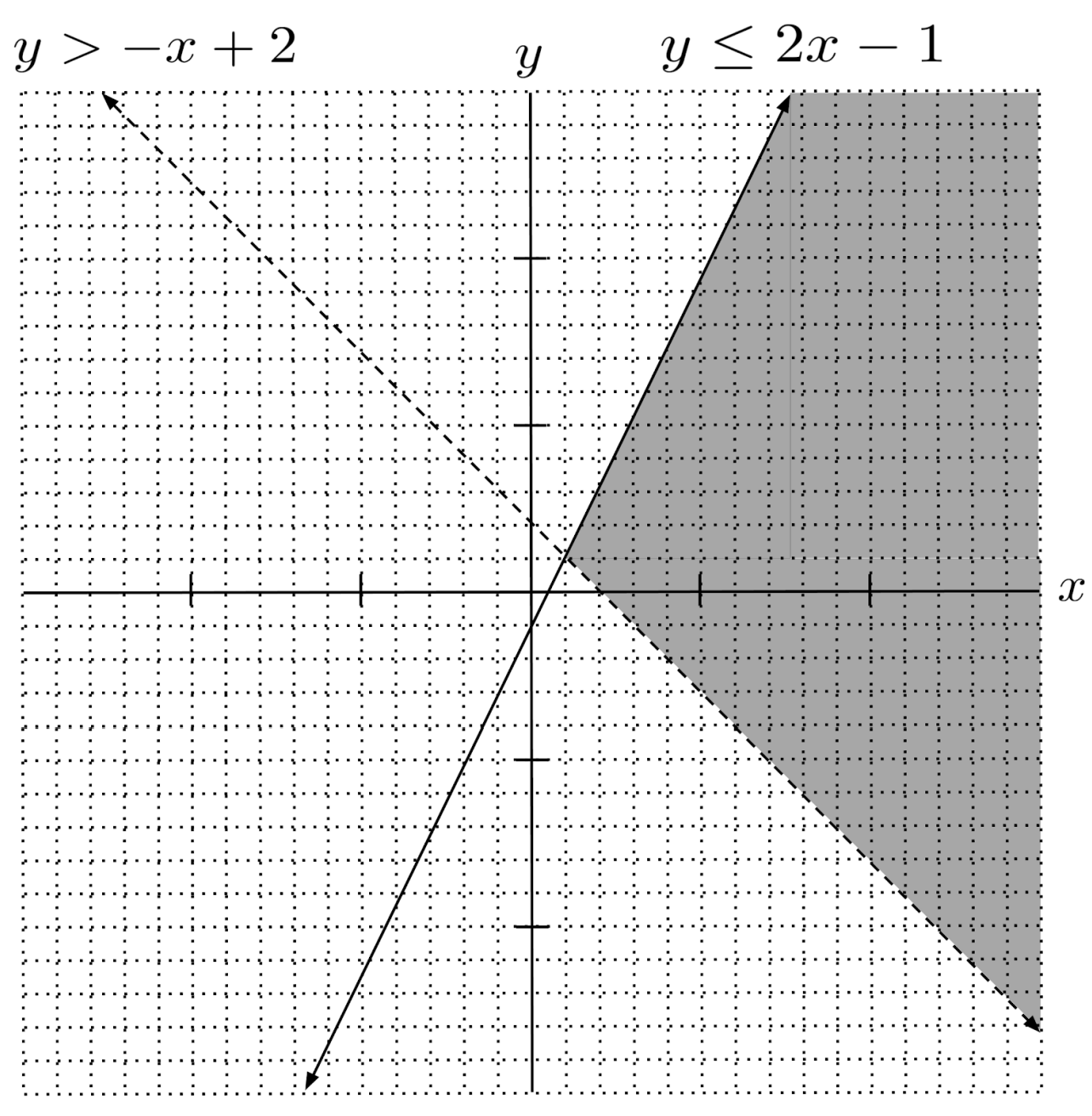
To display the solution to the system, we erase any other shading and shade only the overlap.

Including Another Inequality

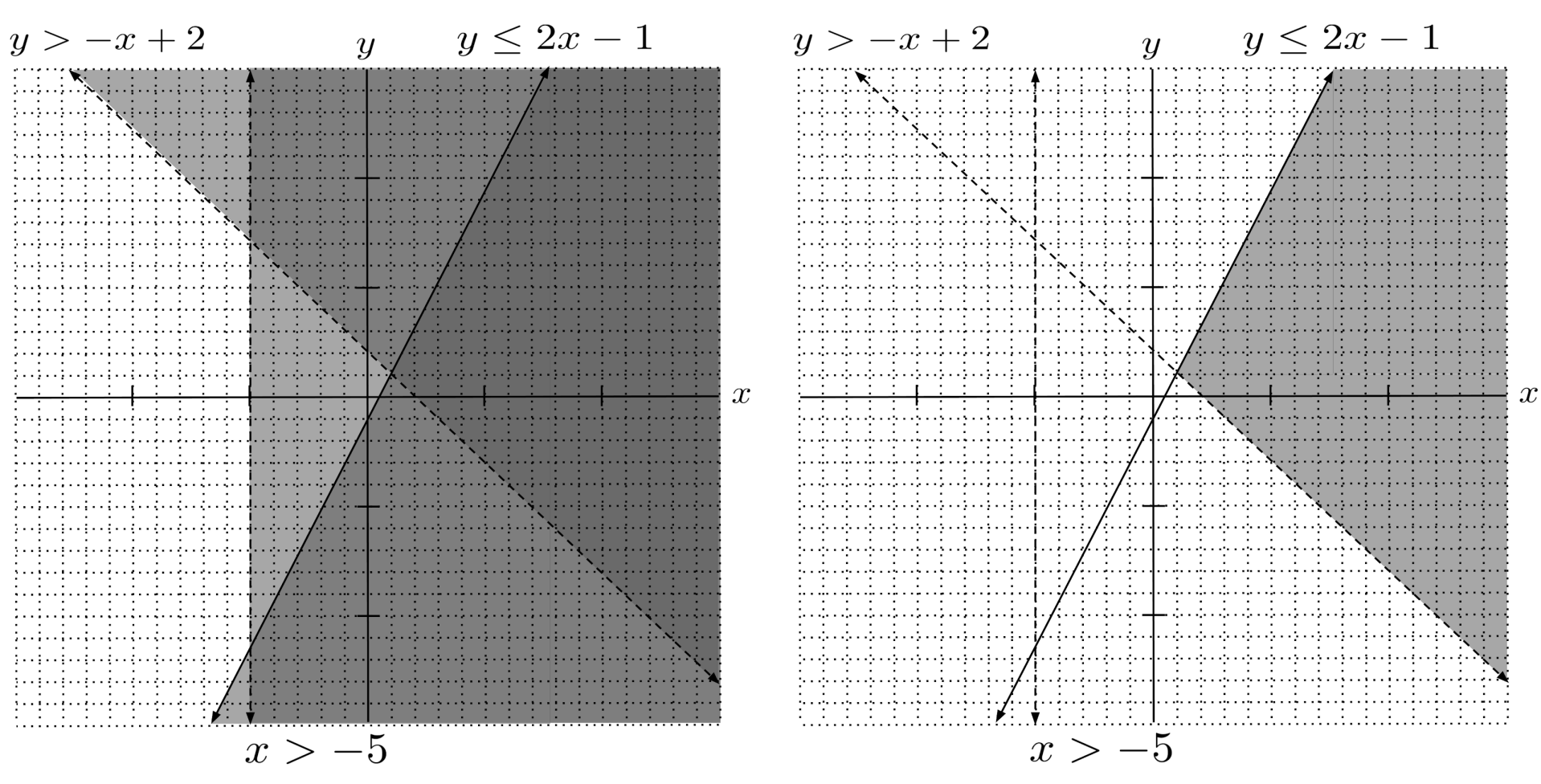
If we include another inequality in the system, then the solution region will either stay the same or shrink.

For example, if we include $x>-5$, then the solution region will stay the same because it is fully contained in the shading of $x>-5$.

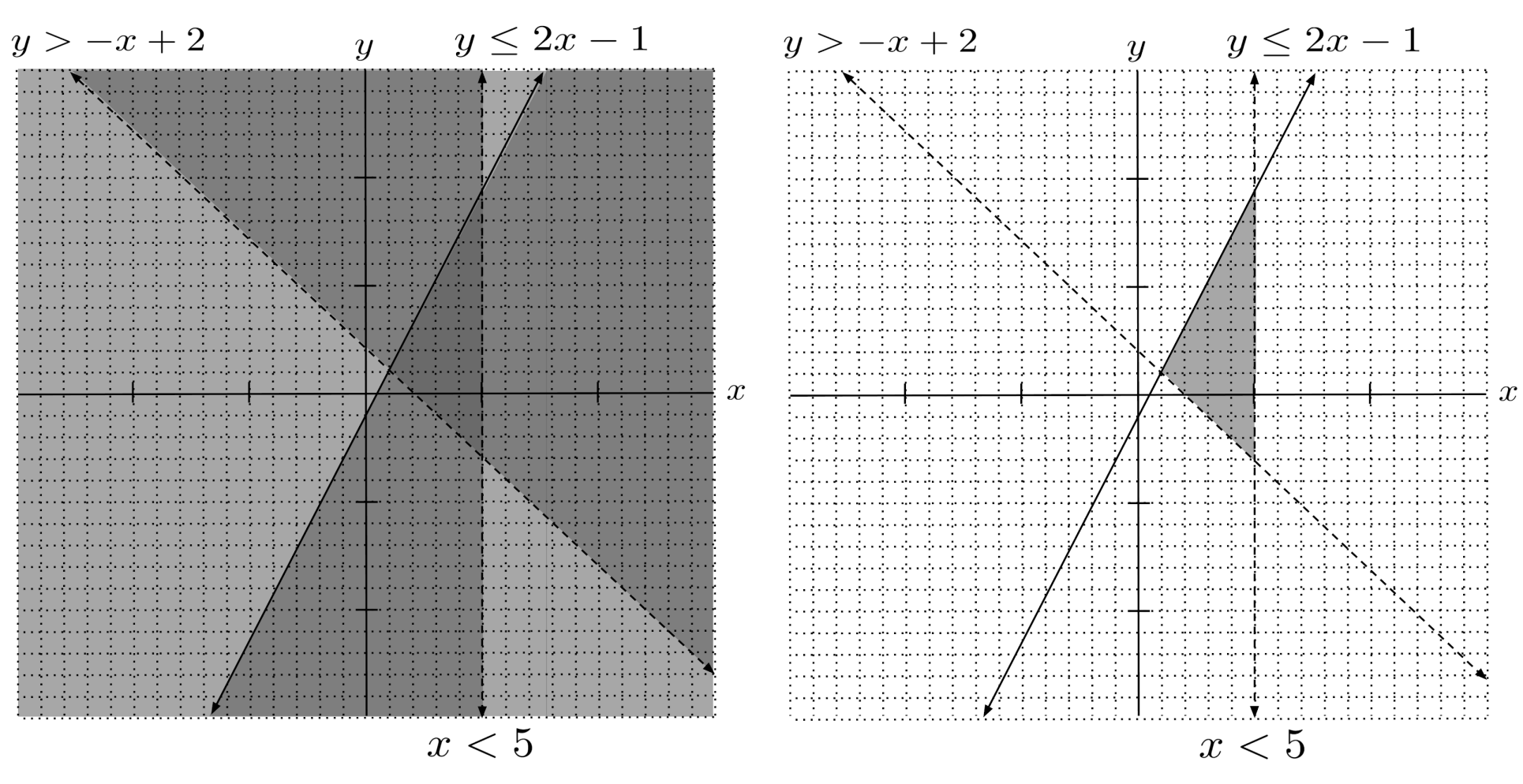
However, if we include $x<5$, then the solution region will shrink because only part of it is contained in the shading of $x<5$.

Quadratic Inequalities

Even with quadratic inequalities, the method is the same: the solution is the overlap of the shading of the component inequalities. Some examples are shown below.

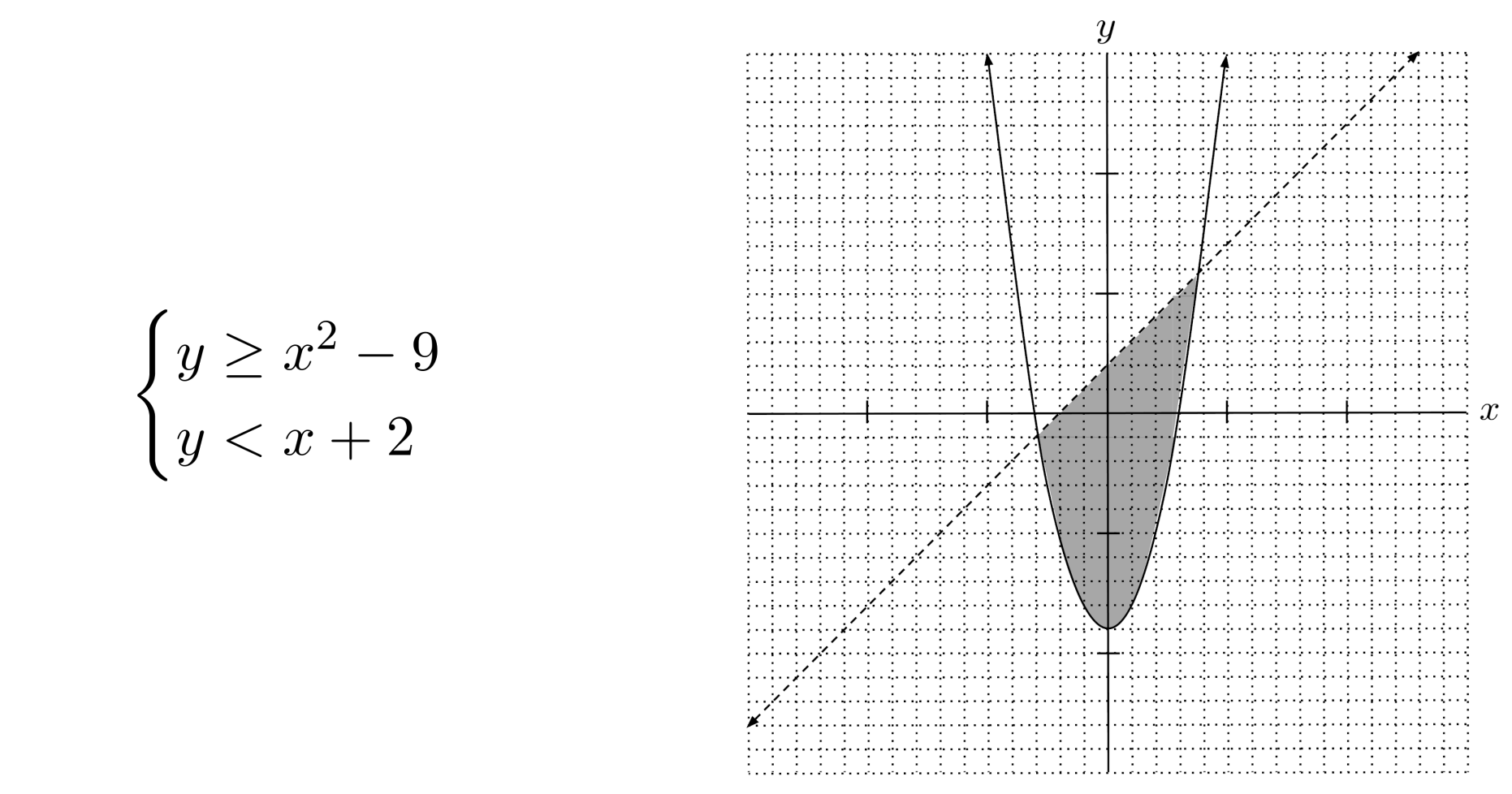
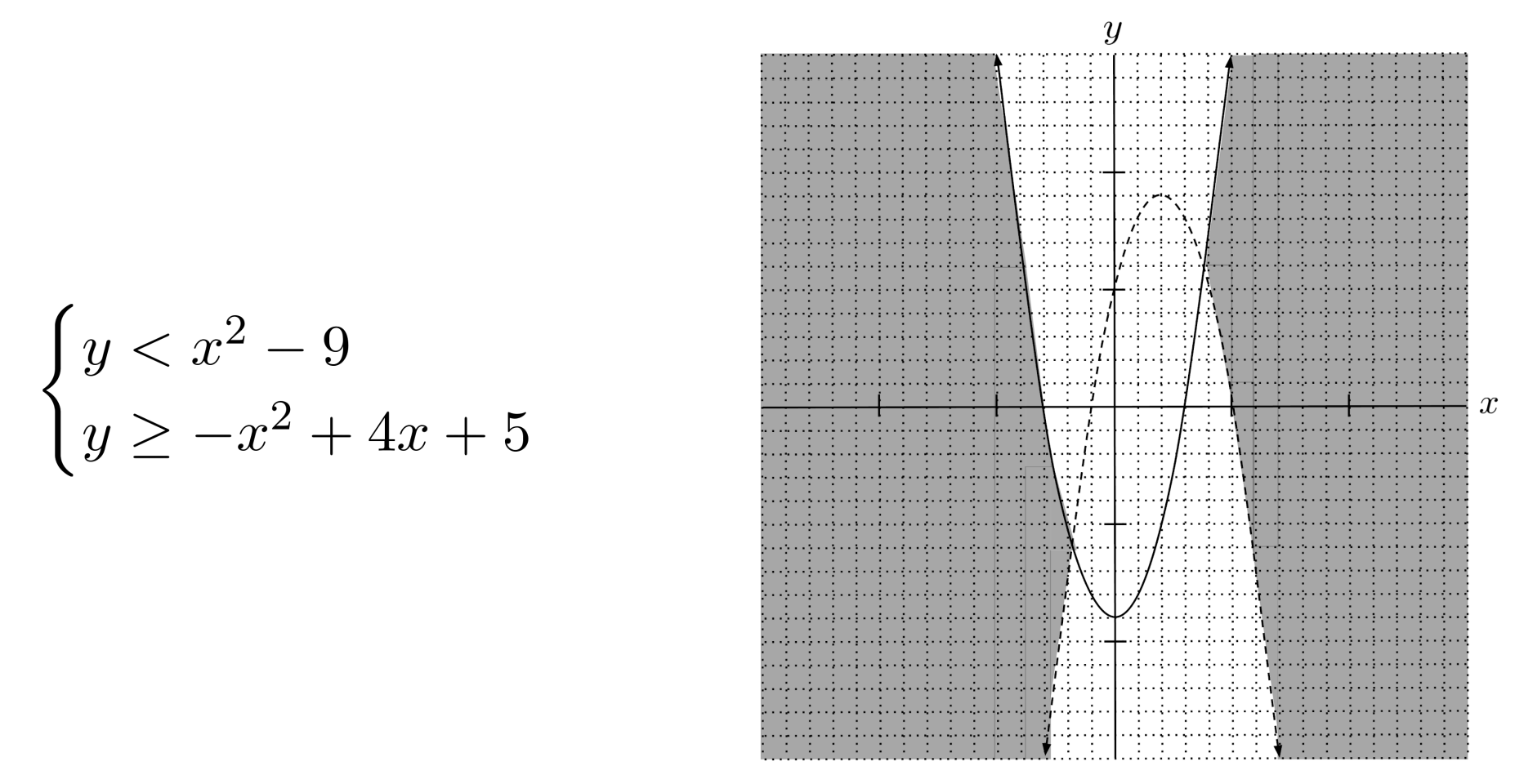
Exercises

Graph the solutions to the systems below. (You can view the solution by clicking on the problem.)

$1) \hspace{.5cm} \begin{cases} y \geq 3x-7 \\ y < -2x+1 \end{cases}$

Solution:

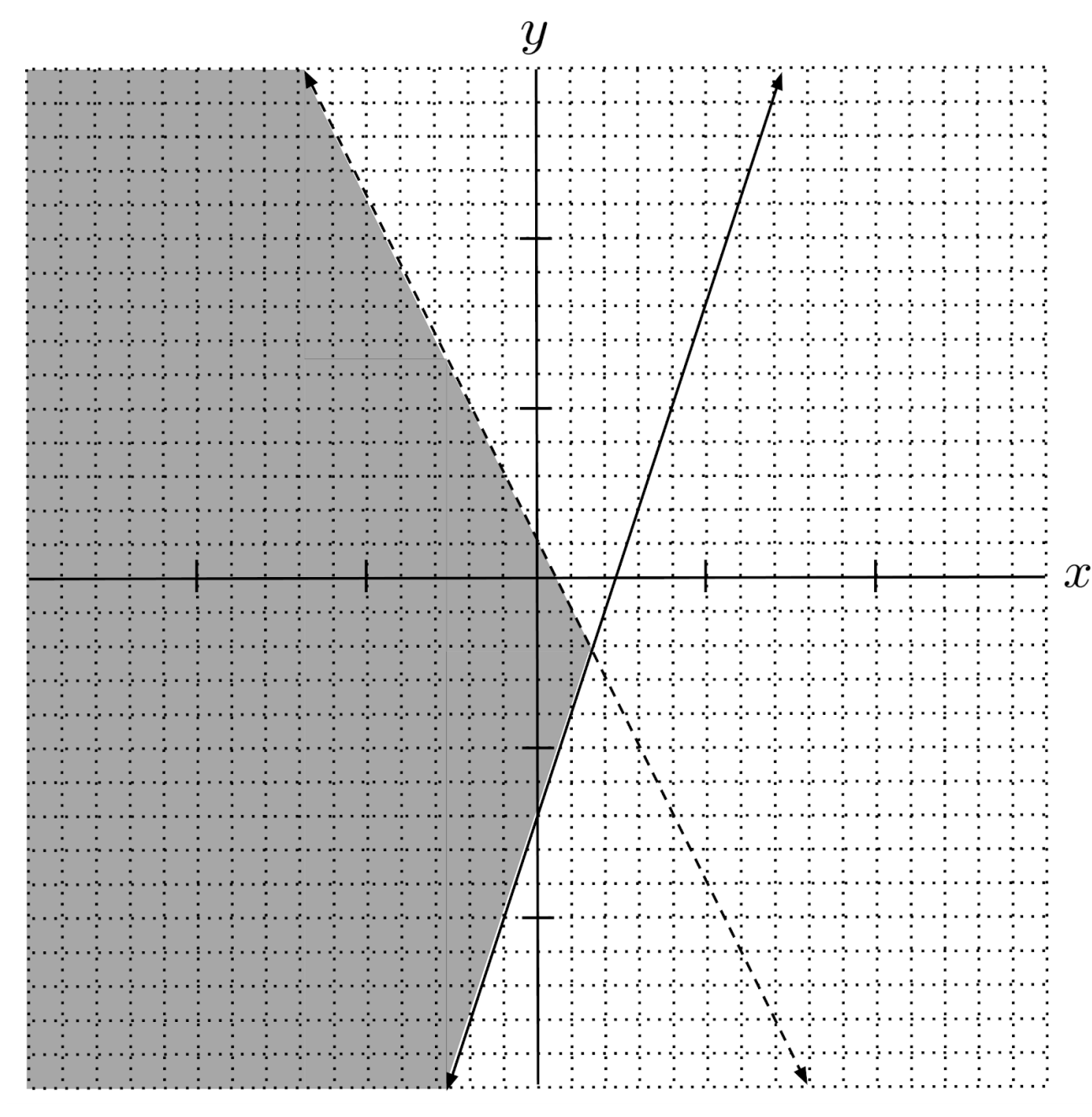
$1) \hspace{.5cm} \begin{cases} y \geq 3x-7 \\ y < -2x+1 \end{cases}$

Solution:

$2) \hspace{.5cm} \begin{cases} y < \frac{1}{3}x-3 \\ y < -5x+5 \end{cases}$

Solution:

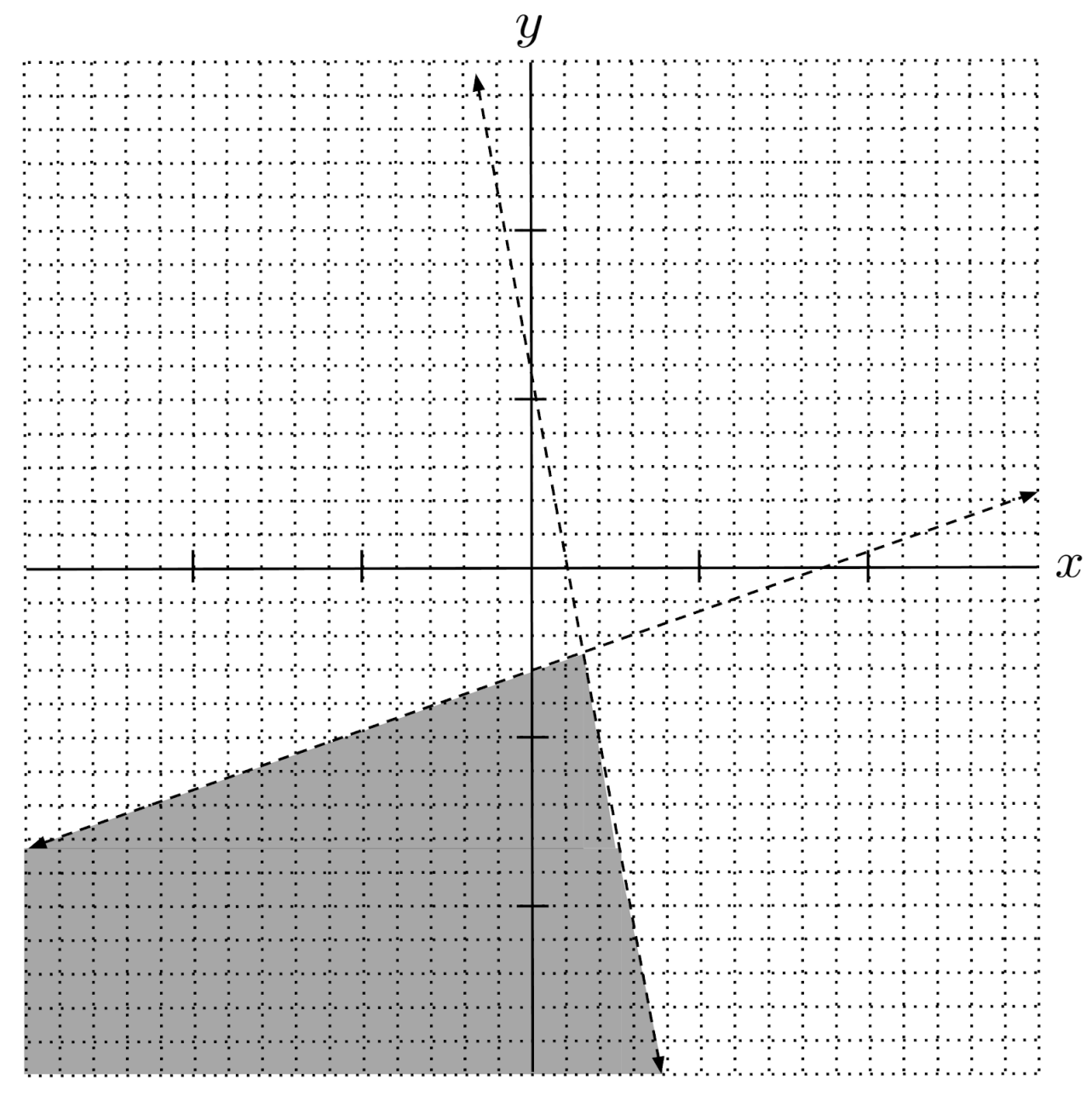
$3) \hspace{.5cm} \begin{cases} y \geq 2x+1 \\ y \leq 8 \end{cases}$

Solution:

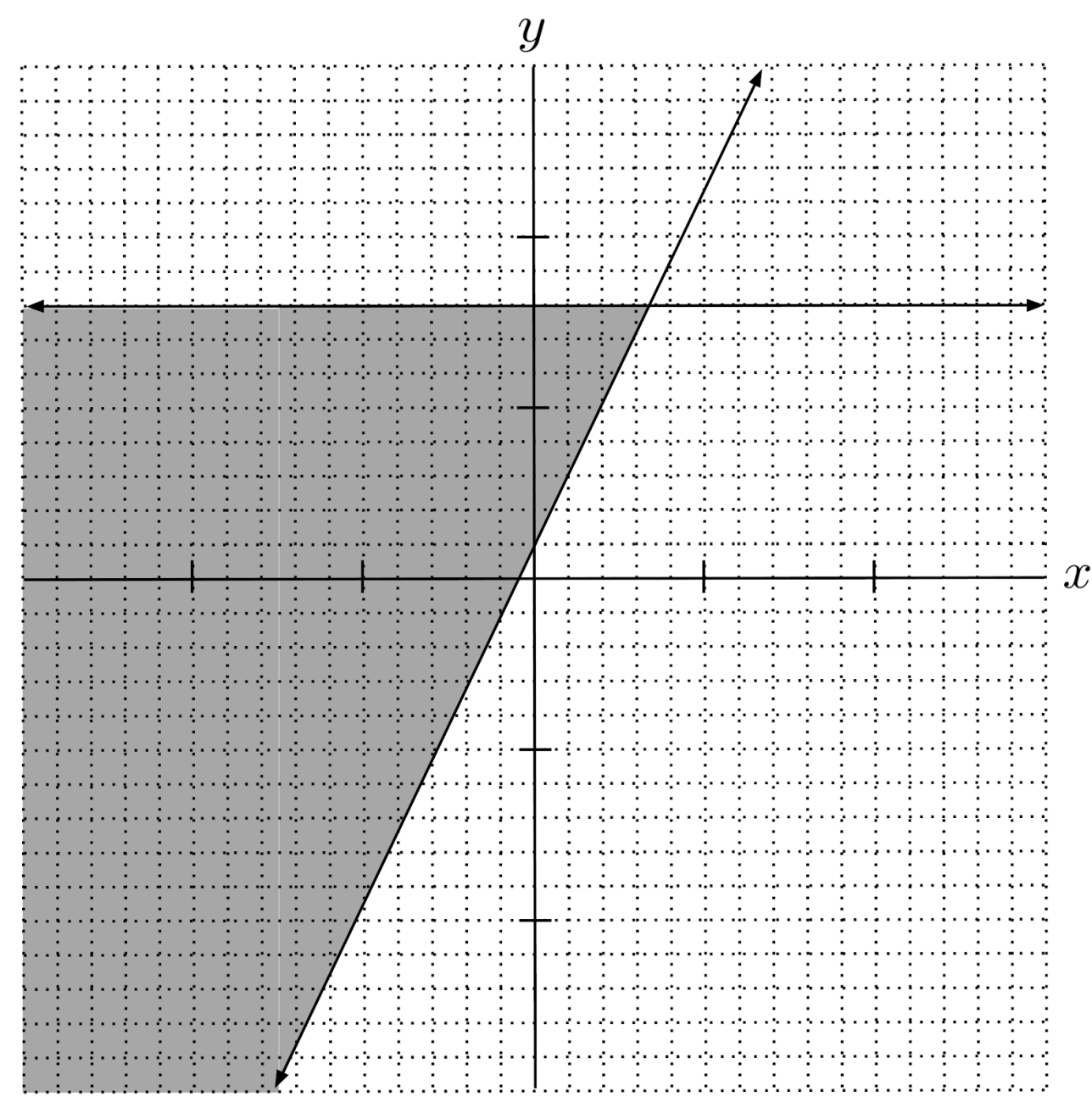
$4) \hspace{.5cm} \begin{cases} x > -5 \\ y > x-3 \\ y < 0 \end{cases}$

Solution:

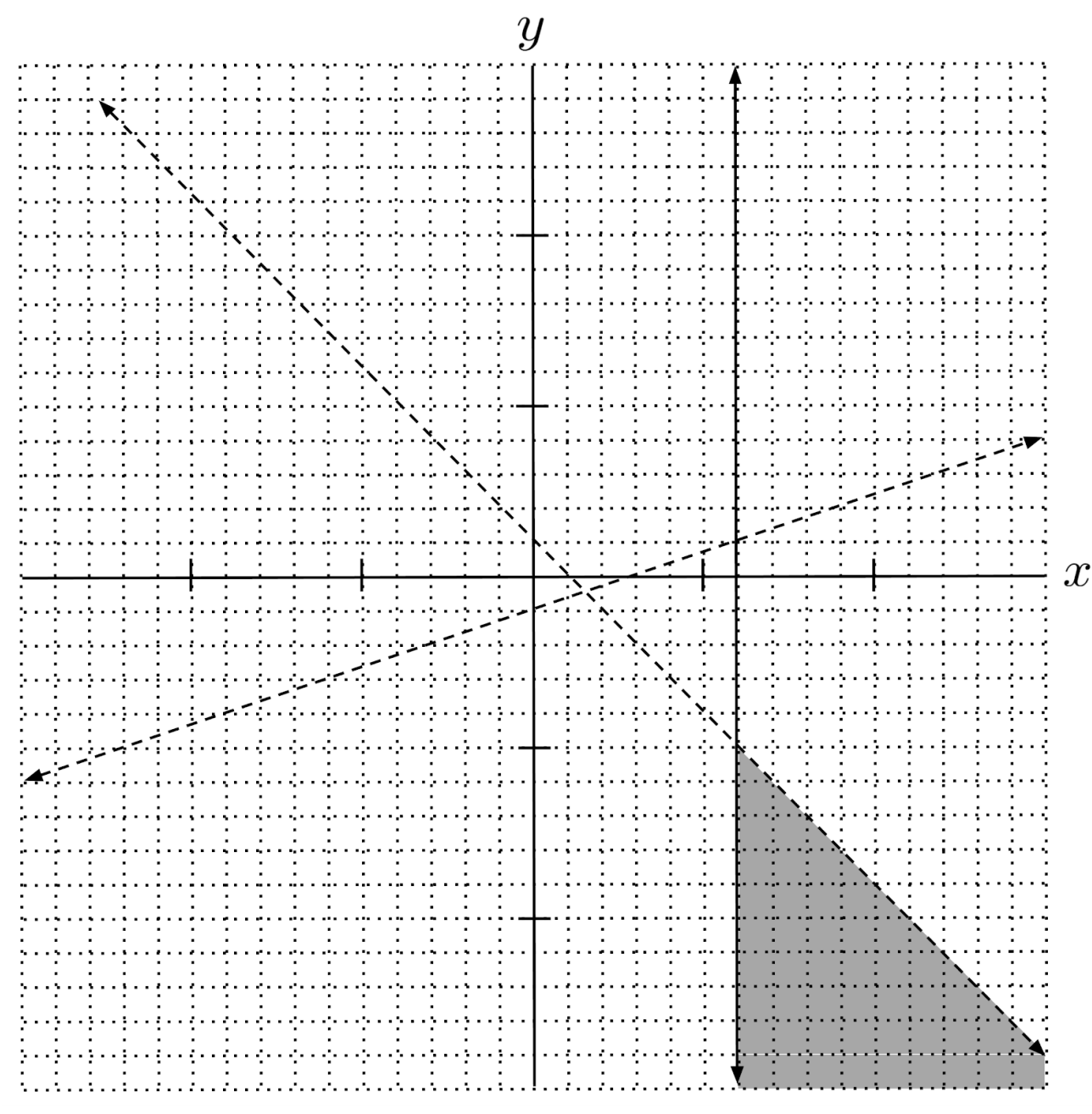
$5) \hspace{.5cm} \begin{cases} x+y<1 \\ 3y<x-3 \\ 2(x-3) \geq x \end{cases}$

Solution:

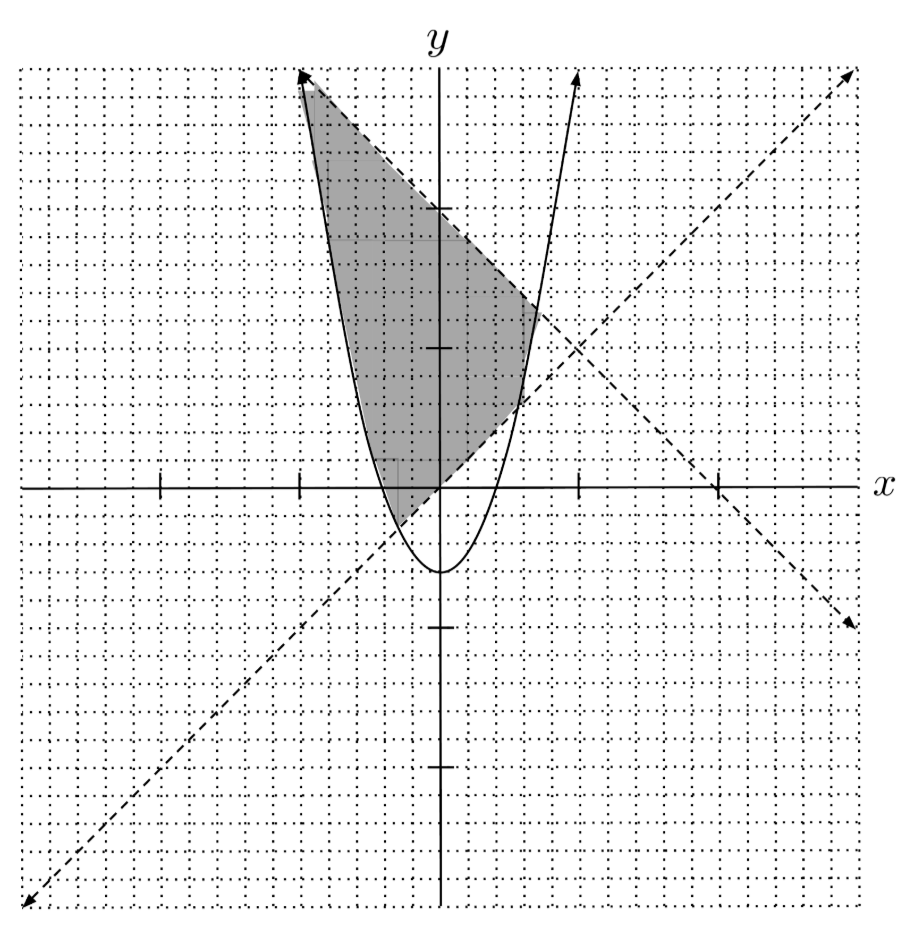
$6) \hspace{.5cm} \begin{cases} y \geq x^2-4 \\ y<10-x \\ y-x>0 \end{cases}$

Solution:

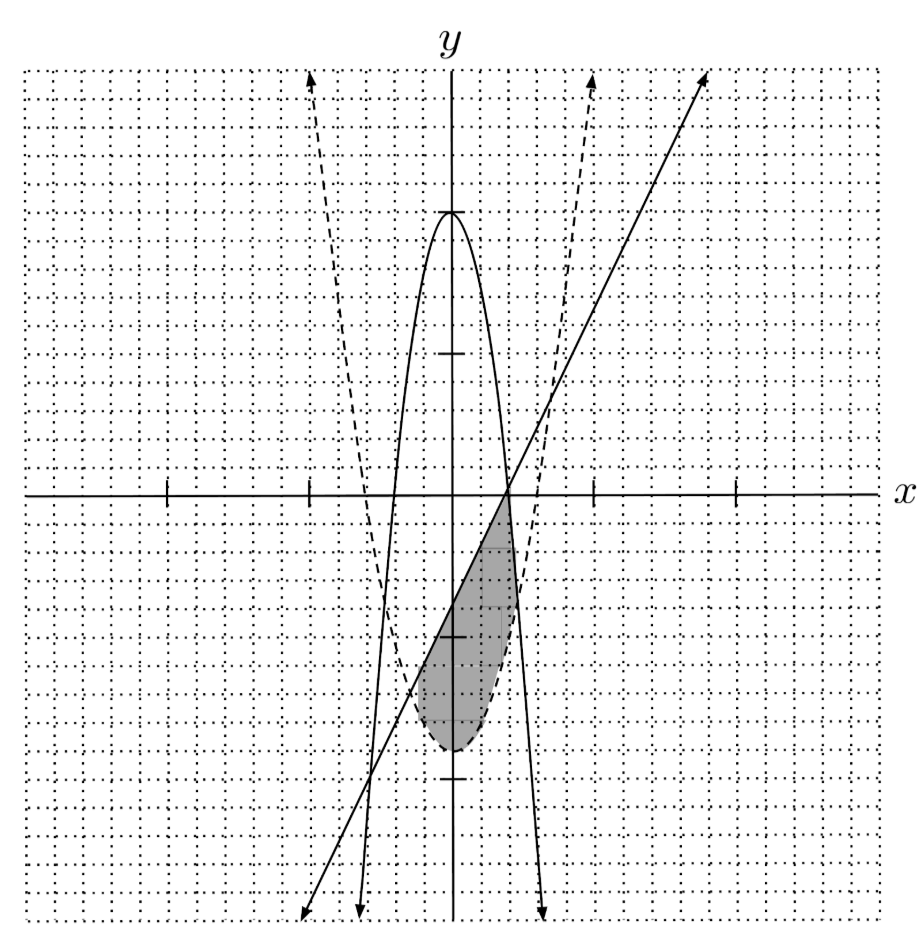
$7) \hspace{.5cm} \begin{cases} 2y+5x^2 \leq 20 \\ y+9>x^2 \\ 2x-y \geq 4 \end{cases}$

Solution:

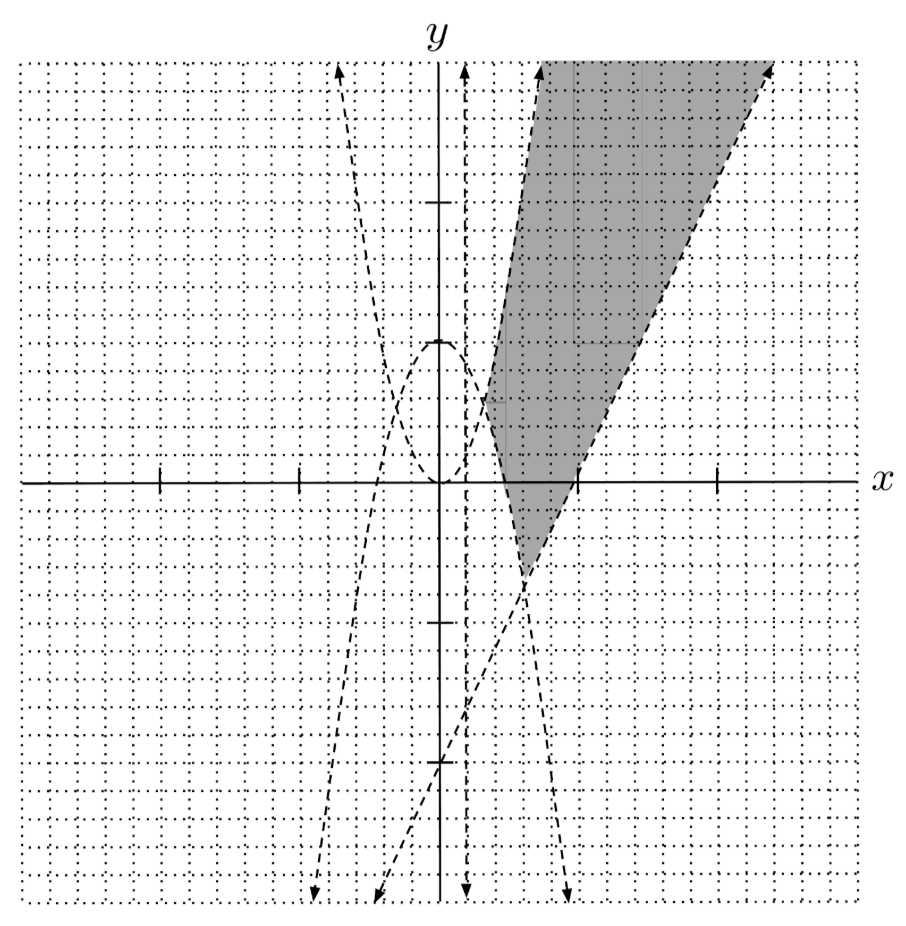
$8) \hspace{.5cm} \begin{cases} y<x^2 \\ y+x^2>5 \\ y>2(x-5) \\ x>1 \end{cases}$

Solution:

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Systems of Inequalities. In Justin Math: Algebra. https://justinmath.com/systems-of-inequalities/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.