Standard Form of a Line

Standard form makes it easy to see the intercepts of a line.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Standard Form of a Line. In Justin Math: Algebra. https://justinmath.com/standard-form-of-a-line/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

The standard form of a linear equation is $ax+by=c$, where $a$, $b$, and $c$ are all integers and $a$ is nonnegative.

For example, we can convert the equation $y=\frac{3}{5}x+\frac{10}{3}$ to standard form by moving $x$ and $y$ to the same side and multiplying to cancel out any fractions.

Finding the Intercepts

Standard form makes it easy to see the intercepts of the line: to get the x-intercept in $ax+by=c$, we divide the constant $c$ by the x-coefficient $a$, and to get the y-intercept, we divide the constant $c$ by the y-coefficient $b$.

For example, the x-coefficient of $9x-15y=-50$ is $-\frac{50}{9}$, and the y-coefficient is $\frac{-50}{-15}$ which simplifies to $\frac{10}{3}$.

This trick for finding the intercepts works because finding the intercept of a particular variable involves substituting $0$ for the other variable. The x-intercept occurs at some point $(x,0)$ where $y$ is $0$, so to solve for the x-intercept, we can substitute $0$ for $y$ and solve for $x$.

Likewise, the y-intercept occurs at some point $(0,y)$ where $x$ is $0$, so to solve for the y-intercept, we can substitute $0$ for $x$ and solve for $y$.

Graphing

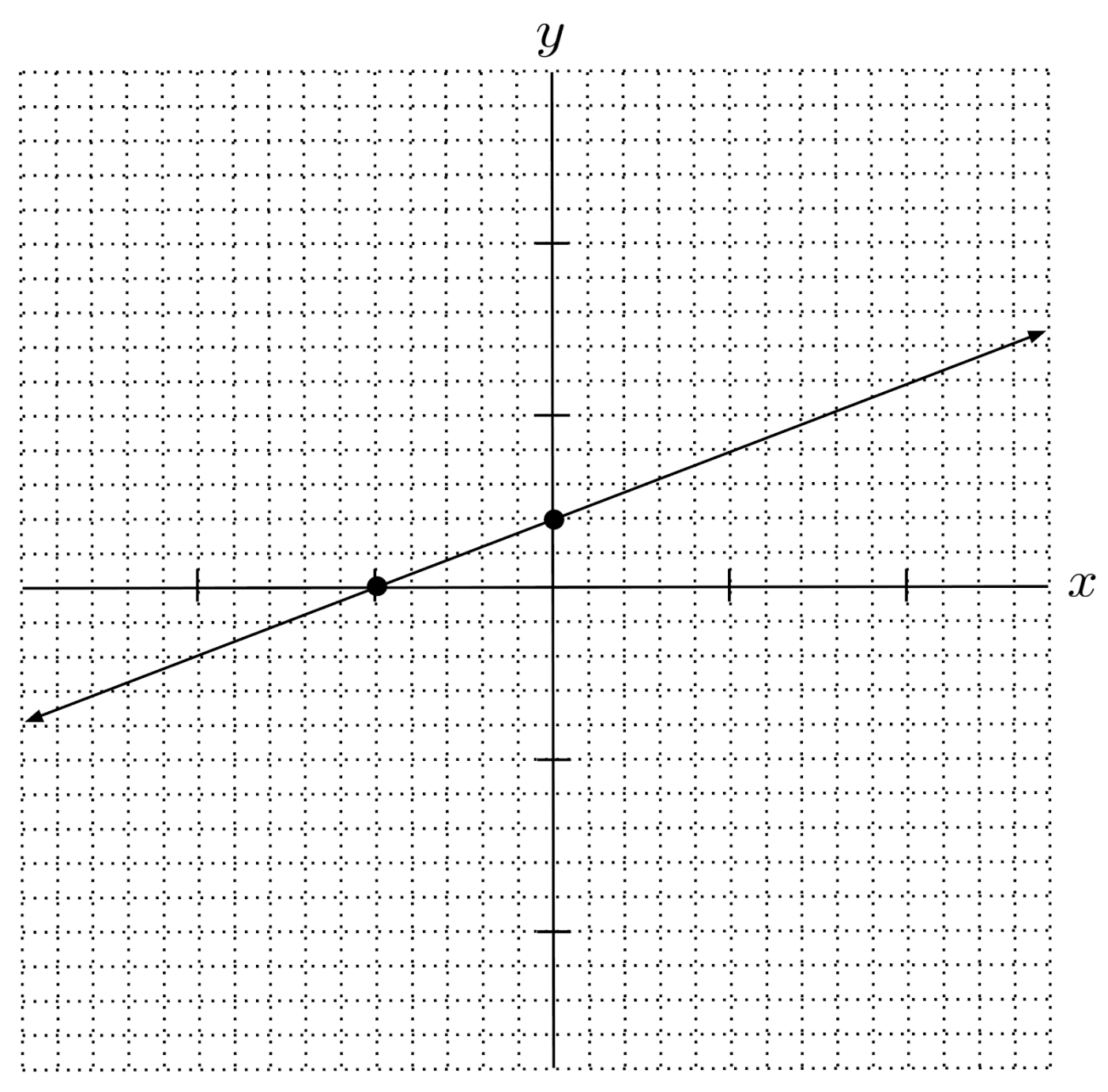
To plot the line, then, all we have to do is mark the intercepts and then draw a line through them.

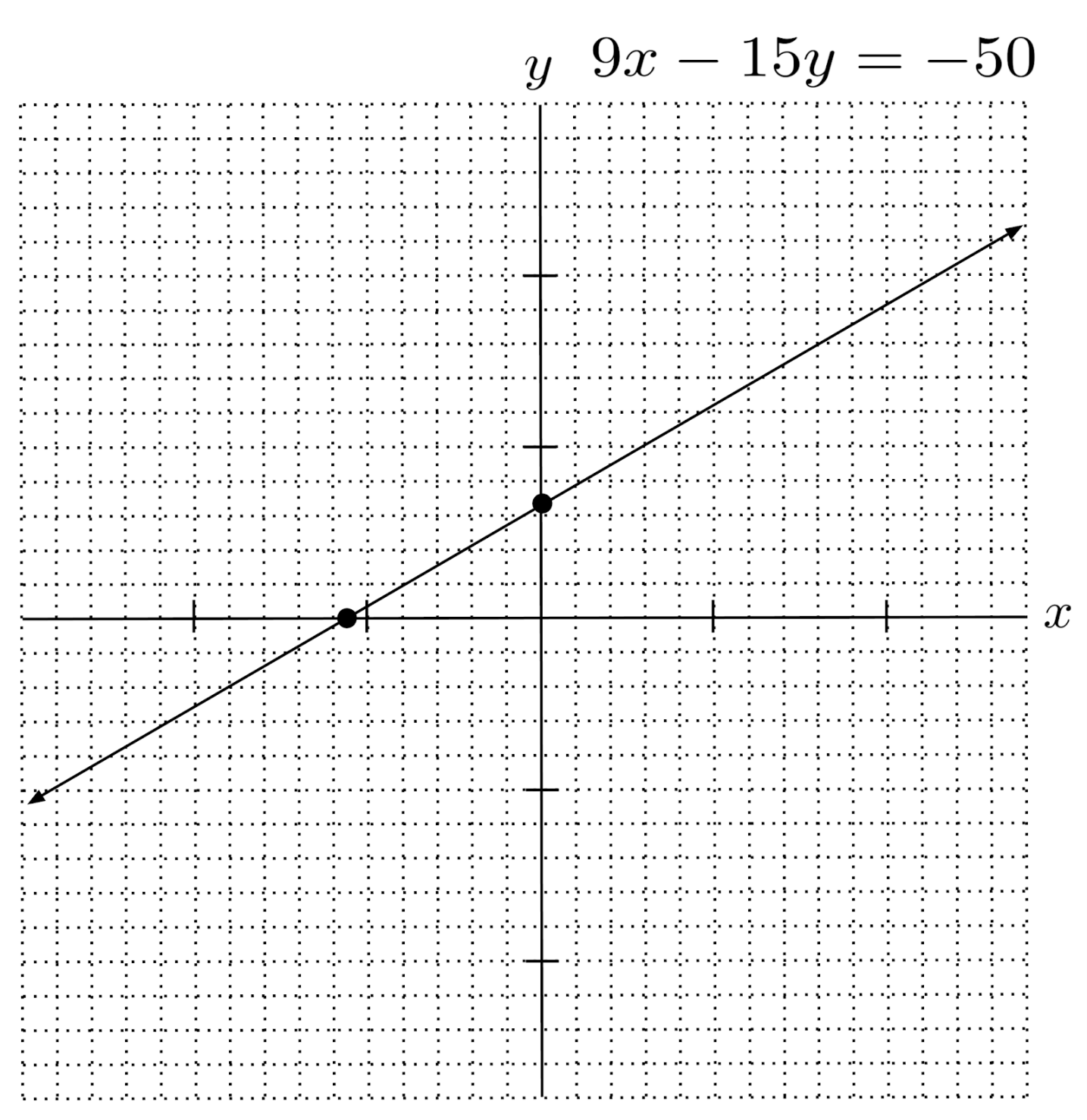
For example, in the line $9x-15y=-50$, we computed the x-intercept as $-\frac{50}{9}$, or $-5 \frac{5}{9}$, and the y-intercept as $\frac{10}{3}$, or $3 \frac{1}{3}$.

To graph the line, we just need to plot the intercepts $\left( -5 \frac{5}{9},0 \right)$ and $\left( 0,3 \frac{1}{3} \right)$ and draw a line through them.

Exercises

Write the equation in standard form. (You can view the solution by clicking on the problem.)

Graph the following by drawing a line through the intercepts. (You can view the solution by clicking on the problem.)

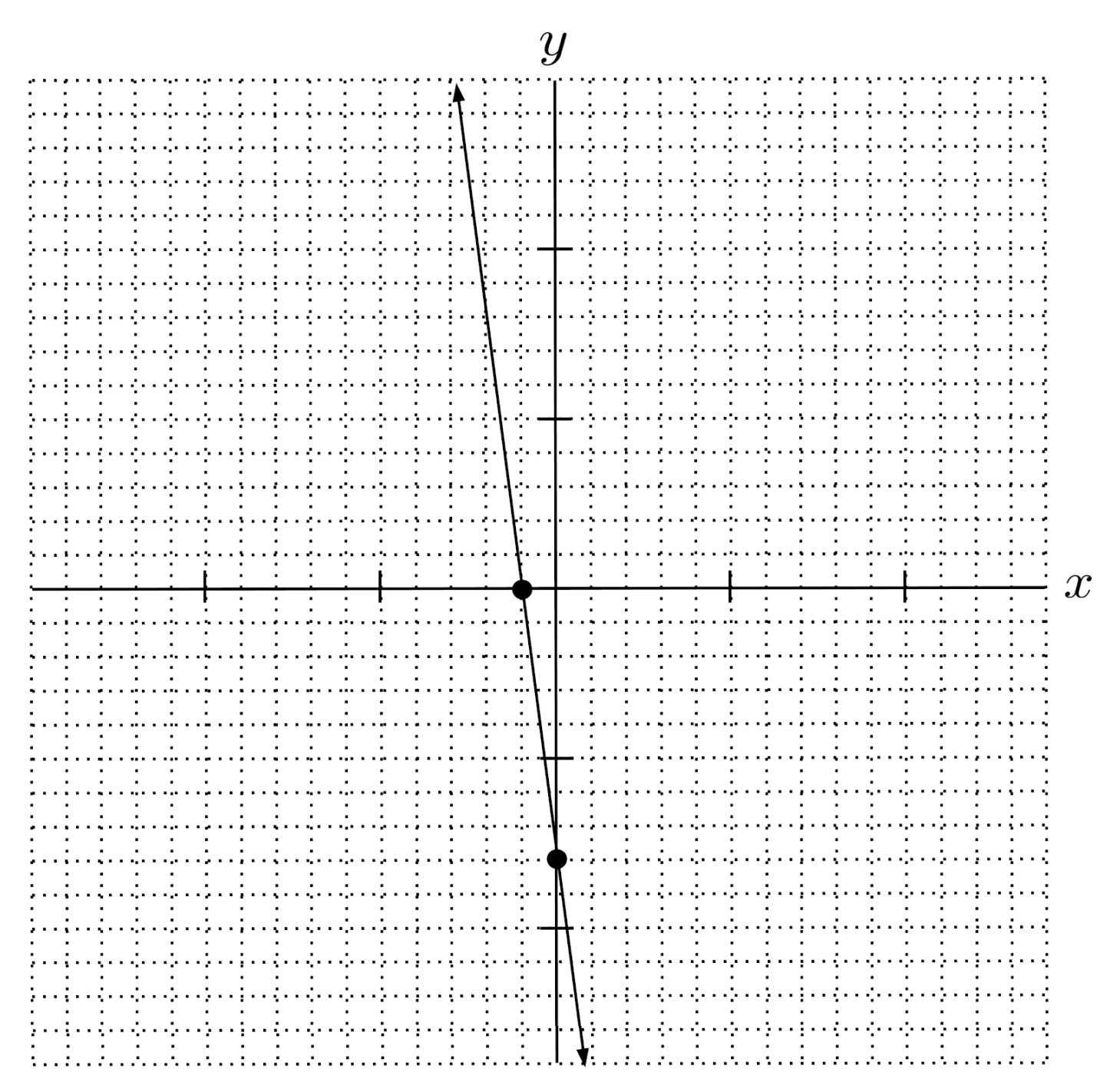
$7) \hspace{.5cm} y-2=3(x-4)$

Solution:

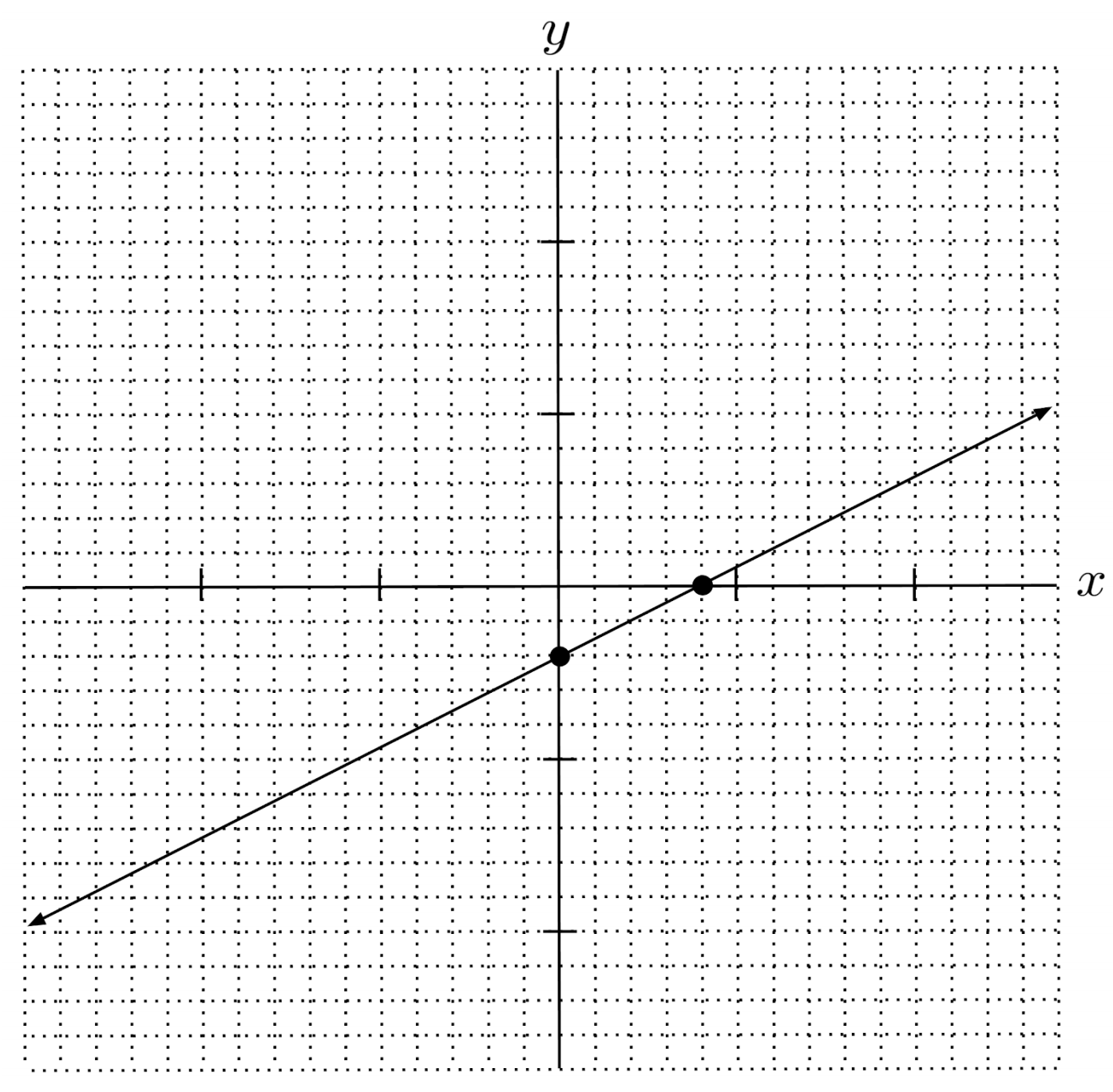
$8) \hspace{.5cm} y+7=-2(x-2)$

Solution:

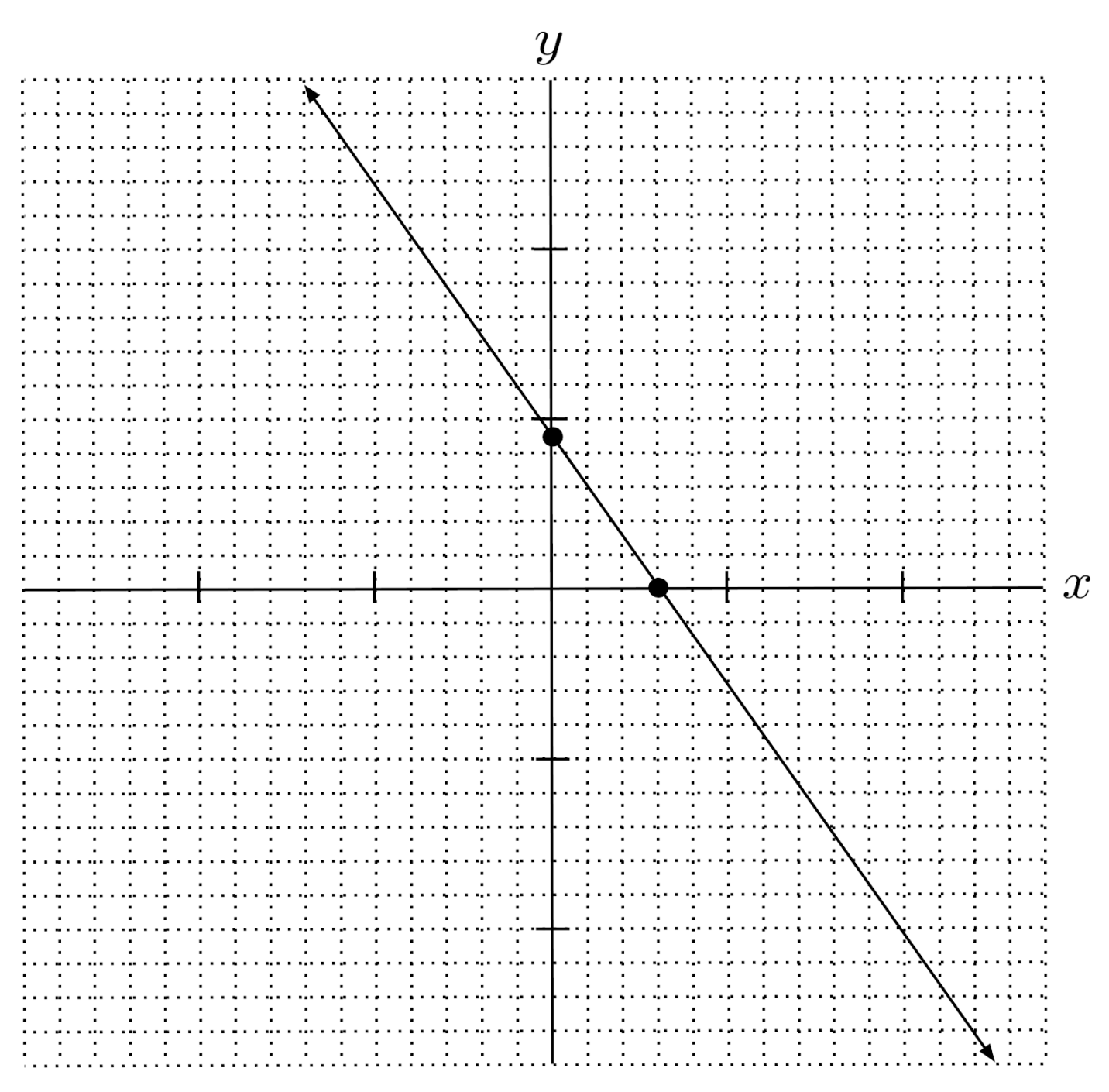
$9) \hspace{.5cm} y-\frac{1}{2} = \frac{1}{3}(x+1)$

Solution:

$10) \hspace{.5cm} y+\frac{5}{2} = -\frac{2}{5}\left( x-\frac{1}{4} \right)$

Solution:

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Standard Form of a Line. In Justin Math: Algebra. https://justinmath.com/standard-form-of-a-line/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.