Standard Form and End Behavior of Polynomials

by Justin Skycak (@justinskycak) on April 01, 2018

The end behavior of a polynomial refers to the type of output that is produced when we input extremely large positive or negative values.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Standard Form and End Behavior of Polynomials. In Justin Math: Algebra. https://justinmath.com/standard-form-and-end-behavior-of-polynomials/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Polynomials include linear expressions and quadratic expressions, as well as expressions adding multiples of higher exponents of the variable. Rational functions are usually written in proper form, where the numerator is of a smaller degree than the denominator. (The degree of a polynomial is its highest exponent.)

For example, these are polynomials:

$\begin{align*} x^5-4x^2+1 \hspace{1.5cm} 3x^4+(x+1)^3 \hspace{1.5cm} x^6+(x^2-1)^3+x+1 \end{align*}$

On the other hand, these are not polynomials:

$\begin{align*} x^2+\sqrt{x}+1 \hspace{1.5cm} \sin(x)+x^3-2 \hspace{1.5cm} |x|+x^5+x^3-1 \end{align*}$

Standard Form

Polynomials are usually written in standard form, in which all terms are fully expanded and variable exponents are arranged from greatest to least.

$\begin{align*} \text{Original polynomial} \hspace{.5cm} &\Bigg| \hspace{.5cm} x(5+2x^2)(x-1)+3(4+x^3) \\ \text{Simplify} \hspace{.5cm} &\Bigg| \hspace{.5cm} x(5x-5+2x^3-2x^2)+12+3x^3 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} 5x^2-5x+2x^4-2x^3+12+3x^3 \\ \text{Combine like terms} \hspace{.5cm} &\Bigg| \hspace{.5cm} 5x^2-5x+2x^4+x^3+12 \\ \begin{matrix} \text{Arrange exponents from} \\ \text{greatest to least} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} 2x^4+x^3+5x^2-5x+12 \end{align*}$

End Behavior

The end behavior of a polynomial refers to how it behaves when we substitute extremely large positive or negative values for $x$.

If the polynomial evaluates to a very large positive number, we say it approaches infinity. Otherwise, if the polynomial evaluates to a very large negative number, we say it approaches negative infinity.

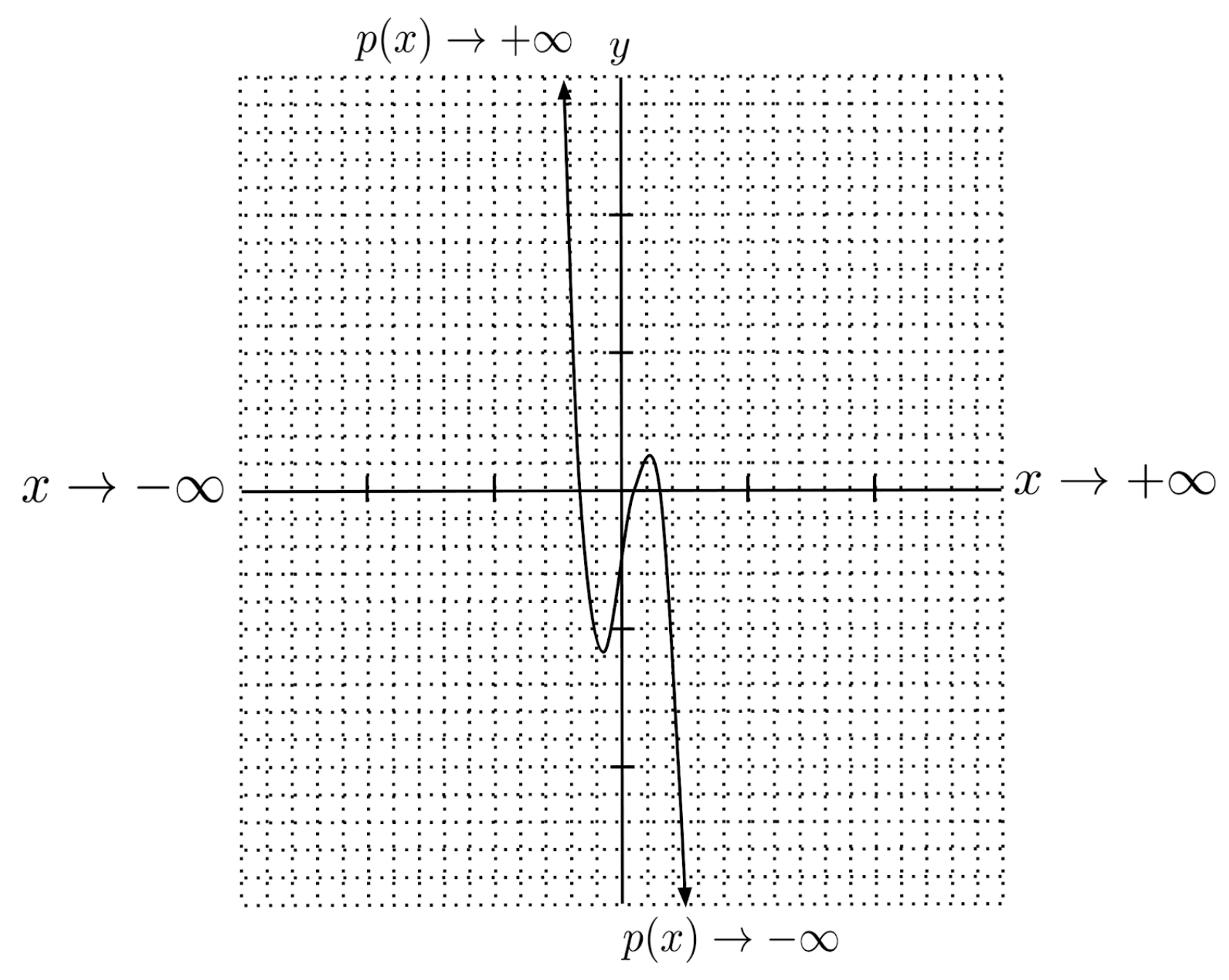
For example, consider the polynomial $p(x)=-2x^3+x^2+5x-3$. When we substitute a large positive number, such as $x=100$, the output is a large negative number.

$\begin{align*} p(100) &= -2(100)^3+(100)^2+5(100)-3 \\ &= -2(1000000) + 10000 + 500 - 3 \\ &= -2000000 + 10000 + 500 - 3 \\ &= -1989503 \end{align*}$

When we substitute a large negative number, such as $x=-100$, the output is a large positive number.

$\begin{align*} p(100) &= -2(-100)^3+(-100)^2+5(-100)-3 \\ &= -2(-1000000) + 10000 - 500 - 3 \\ &= 2000000 + 10000 - 500 - 3 \\ &= 2009497 \end{align*}$

Putting this together, we say that $p(x)$ goes to negative infinity as $x$ goes to positive infinity, and $p(x)$ goes to positive infinity as $x$ goes to negative infinity.

We can write this symbolically: $p(x) \to -\infty$ as $x \to +\infty$, and $p(x) \to +\infty$ as $x \to -\infty$. This is the end behavior of the polynomial $p(x)$.

Graphical Interpretation

Graphically, end behavior tells us whether the polynomial curves up or down as we travel away from the origin in the right or left direction.

Since $p(x) \to -\infty$ as $x \to +\infty$, we know that the polynomial curves down as we travel to the right, and since $p(x) \to +\infty$ as $x \to -\infty$, we know that the polynomial curves up as we travel to the left.

Shortcuts

Do you notice any patterns or shortcuts? It’s possible to determine the end behavior of a polynomial without evaluating the full polynomial.

The term with the highest exponent controls the end behavior, because it makes the greatest contribution to the result. All the other terms make much smaller contributions – they’re peanuts in comparison to the highest-exponent term.

$\begin{align*} p(100) &\approx -2(100)^3 = -2000000 \\ p(-100) &\approx -2(-100)^3 = 2000000 \end{align*}$

But we can do even better – we don’t actually have to evaluate anything at all! Within the term having the highest exponent, we just need to look at the exponent and sign of the coefficient. If the exponent is even, then the result after exponentiation will always be positive. Consequently, the term will evaluate to have the same sign as its coefficient.

For example, to find the end behavior of the polynomial $p(x)=2x^2-3x+4$, we just need to look at the $2x^2$ term. Since the exponent is even, $x^2$ will always be positive – if we substitute $x=100$, then $x^2=10000$, and if we substitute $x=-100$, then $x^2=10000$ again. The coefficient $2$ is also positive, so $2x^2$ is always a positive times a positive, which makes a positive. As a result, we have $p(x) \to +\infty$ as $x \to +\infty$ and $p(x) \to +\infty$ as $x \to -\infty$.

Likewise, to find the end behavior of the polynomial $p(x) = -5x^4+7x^3-x-2$, we just need to look at the $-5x^2$ term. Since the exponent is even, $x^4$ will always be positive – if we substitute $x=100$, then $x^4=100000000$, and if we substitute $x=-100$, then $x^4=100000000$ again. But the coefficient $-5$ is negative, so $-5x^4$ is always a negative times a positive, which makes a negative. As a result, we have $p(x) \to -\infty$ as $x \to +\infty$ and $p(x) \to -\infty$ as $x \to -\infty$.

Examples with an Odd Exponent

On the other hand, if the exponent is odd, then the result after exponentiation will always have the same sign as the input $x$. Consequently, the term will evaluate to be positive if the coefficient and the input $x$ have the same sign, and negative if they have opposite signs.

For example, to find the end behavior of the polynomial $p(x) = 4x^3-5x^2-2x+1$, we just need to look at the $4x^3$ term. Since the exponent is odd, exponentiation will not change the sign – if we substitute $x=100$, then $x^3=1000000$, and if we substitute $x=-100$, then $x^3=-100000000$. The coefficient $4$ is positive, and multiplying by a positive doesn’t change the sign either. As a result, we have $p(x) \to +\infty$ as $x \to +\infty$ and $p(x) \to -\infty$ as $x \to -\infty$.

Likewise, to find the end behavior of the polynomial $p(x)=-3x^5 + 7x^4 + 3x^2 - 10x$, we just need to look at the $-3x^5$ term. Since the exponent is odd, exponentiation will not change the sign – if we substitute $x=100$, then $x^5=10000000000$, and if we substitute $x=-100$, then $x^5=-10000000000$. But the coefficient $-3$ is negative, and multiplying by a negative changes the sign – if $x^5=10000000000$, then $-3x^5=-30000000000$, and if $x^5=-10000000000$, then $-3x^5=30000000000$. As a result, we have $p(x) \to -\infty$ as $x \to +\infty$ and $p(x) \to +\infty$ as $x \to -\infty$.

Exercises

Convert the following polynomials to standard form. Then, write their end behavior symbolically: $p(x) \to \text{__}$ as $x \to +\infty$, and $p(x) \to \text{__}$ as $x \to -\infty$. (You can view the solution by clicking on the problem.)

$1) \hspace{.5cm} p(x)=3x^4-7x+8x^3$

Solution:
$p(x)=3x^4+8x^3-7x$
$p(x) \to +\infty \text{ as } x \to +\infty$
$p(x) \to +\infty \text{ as } x \to -\infty$

$2) \hspace{.5cm} p(x)=1-2x+x^3$

Solution:
$p(x)=x^3-2x+1$
$p(x) \to +\infty \text{ as } x \to +\infty$
$p(x) \to -\infty \text{ as } x \to -\infty$

$3) \hspace{.5cm} p(x)=2+3x^3-x^6-9x^4$

Solution:
$p(x)=-x^6-9x^4+3x^3+2$
$p(x) \to -\infty \text{ as } x \to +\infty$
$p(x) \to -\infty \text{ as } x \to -\infty$

$4) \hspace{.5cm} p(x)=-10x^9-x^3+5x^4-x^2$

Solution:
$p(x)=-10x^9+5x^4-x^3-x^2$
$p(x) \to -\infty \text{ as } x \to +\infty$
$p(x) \to +\infty \text{ as } x \to -\infty$

$5) \hspace{.5cm} p(x)=6x^3-4x^5+1-2x$

Solution:
$p(x)=-4x^5+6x^3-2x+1$
$p(x) \to -\infty \text{ as } x \to +\infty$
$p(x) \to +\infty \text{ as } x \to -\infty$

$6) \hspace{.5cm} p(x)=1+4x^3-5x+x^4$

Solution:
$p(x)=x^4+4x^3-5x+1$
$p(x) \to +\infty \text{ as } x \to +\infty$
$p(x) \to +\infty \text{ as } x \to -\infty$

$7) \hspace{.5cm} p(x)=8x-1+x^4-5x^6-6x^5$

Solution:
$p(x)=-5x^6-6x^5+x^4+8x-1$
$p(x) \to -\infty \text{ as } x \to +\infty$
$p(x) \to -\infty \text{ as } x \to -\infty$

$8) \hspace{.5cm} p(x)=-x^4+x^{11}-3x^8+2$

Solution:
$p(x)=x^{11}-3x^8-x^4+2$
$p(x) \to +\infty \text{ as } x \to +\infty$
$p(x) \to -\infty \text{ as } x \to -\infty$

$9) \hspace{.5cm} p(x)=(x^2+1)(x+1)$

Solution:
$p(x)=x^3+x^2+x+1$
$p(x) \to +\infty \text{ as } x \to +\infty$
$p(x) \to -\infty \text{ as } x \to -\infty$

$10) \hspace{.5cm} p(x)=-(x-1)(x+1)(x-3)$

Solution:
$p(x)=-x^3+3x^2+x-3$
$p(x) \to -\infty \text{ as } x \to +\infty$
$p(x) \to +\infty \text{ as } x \to -\infty$

$11) \hspace{.5cm} p(x)=(2x^5+1)(x^3-2)$

Solution:
$p(x)=2x^8-4x^5+x^3-2$
$p(x) \to +\infty \text{ as } x \to +\infty$
$p(x) \to +\infty \text{ as } x \to -\infty$

$12) \hspace{.5cm} p(x)=x^2(3-2x^4)(x+2)$

Solution:
$p(x)=-2x^7-4x^6+3x^3+6x^2$
$p(x) \to -\infty \text{ as } x \to +\infty$
$p(x) \to +\infty \text{ as } x \to -\infty$

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.