Slope-Intercept Form

Introducing linear equations in two variables.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Slope-Intercept Form. In Justin Math: Algebra. https://justinmath.com/slope-intercept-form/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

In the previous post, we were solving linear equations in one variable. Now, let’s consider linear equations in two variables. A few examples are shown below:

Solutions to Two-Variable Equations

The solution to a two-variable linear equation is no longer just the number(s) that we can substitute for $x$ to make the equation true, but rather the pair(s) $(x,y)$ that we can substitute for $x$ and $y$ to make the equation true.

Two-variable linear equations usually have infinitely many solutions, because we are usually able to solve for one variable in terms of the other.

If we choose $x=2$, then we can make the given equation true by choosing $y=2(2)-4=0$. If we choose $x=10$, then we can make the given equation true by choosing $y=2(10)-4=16$. Whatever value we choose for $x$, we can make the equation true by choosing $y$ as twice that value, minus $4$.

However, although there are infinitely many solutions to the equation, that doesn’t mean that any random pair we pick will be a solution. For example, if we try the pair $(x,y)=(2,1)$, then the left-hand side comes out to $10(2)=5(1)+15=30$, not $35$.

Graphing

To really see what’s going on, it helps to plot the solutions on a graph. In fact, linear equations are called linear because when we plot them on a graph, they form a straight line.

To plot all the solutions of $y=2x-4$ on the graph below, we plot two solutions and draw a line through them. We already saw that one solution was $(2,0)$, and when we substitute $x=0$ we get $y=2(0)-4=-4$, so another solution is $(0,-4)$.

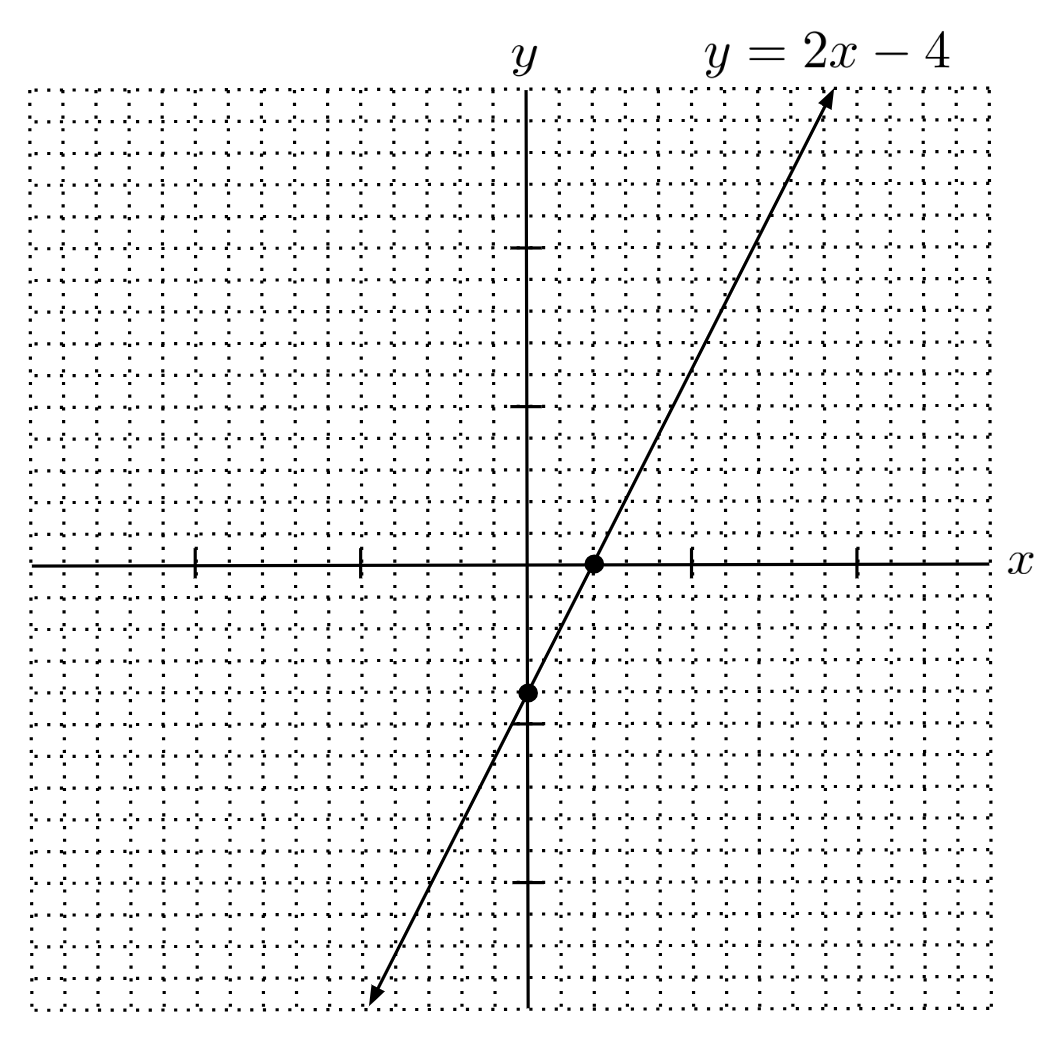
Any point that is on the line is a solution of the original equation. For example, we see that the line passes through the point $(4,4)$ – and indeed, substituting $x=4$ and $y=4$ makes the original equation true.

Slope-Intercept Form

In general, when we solve for $y$ in a linear equation of two variables, we end up with a result in the form $y=mx+b$ where $m$ and $b$ are constants (provided $y$ doesn’t vanish). This is called slope-intercept form, and the constants $m$ and $b$ are called the slope and y-intercept of the line, respectively.

The y-intercept takes its name from the fact that the line crosses the y-axis at $b$. For example, the graph of $y=2x-4$ shown earlier crossed the y-axis at $-4$. This pattern is true in general because the pair $(0,b)$ is a solution of the equation $y=mx+b$: when we substitute $x=0$, we find $y=m(0)+b=b$.

The slope takes its name from the fact that $m$ controls how steep the line is: for every unit the line travels right, it travels $m$ units up (or down, if $m$ is negative). For example, in the graph of $y=2x-4$, if we start at the point $(2,0)$ and travel $1$ unit right and $2$ units up, we arrive at the point $(3,2)$, which is also on the line.

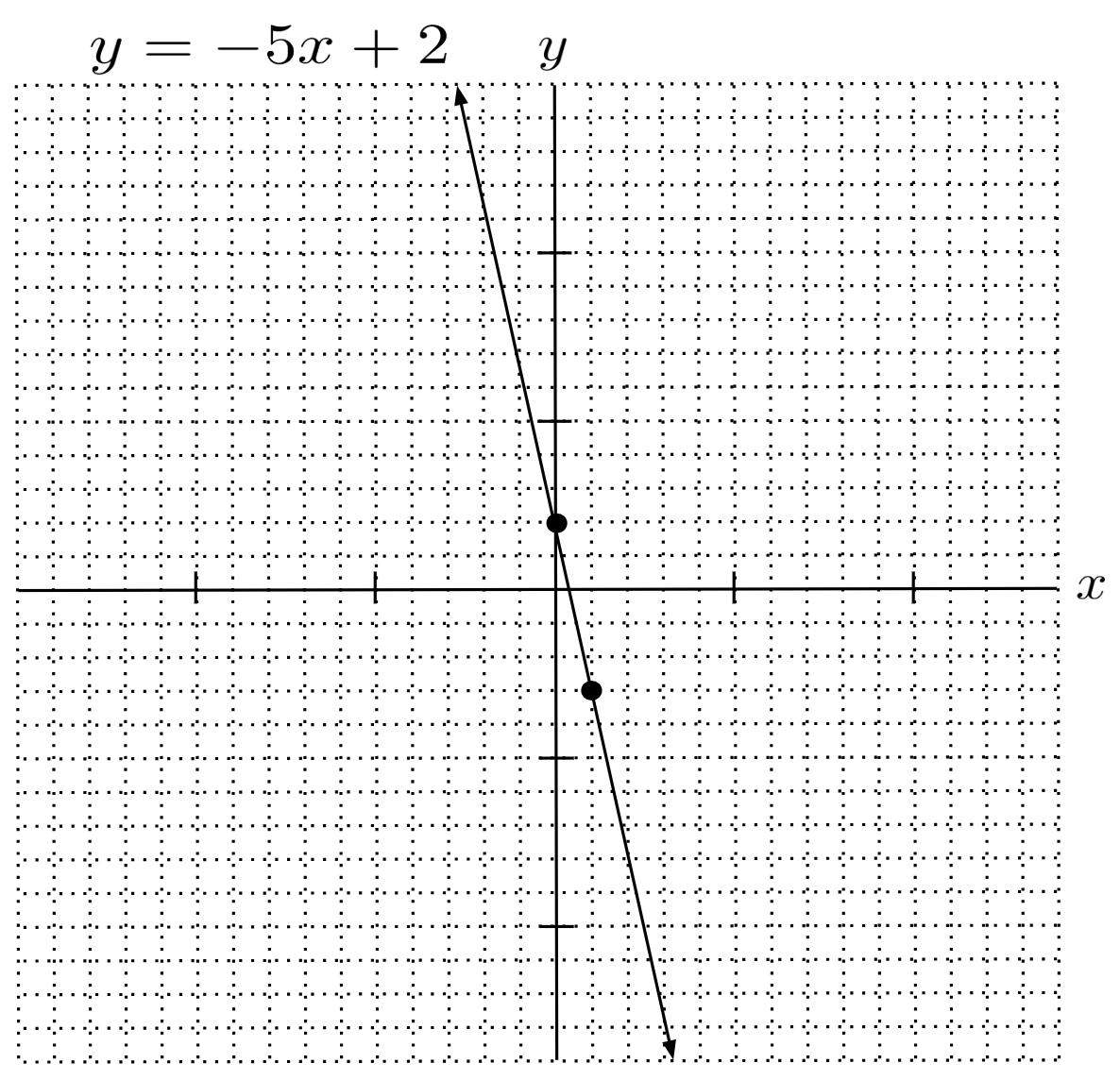
To graph a line $y-mx+b$ in slope-intercept form, it is easiest to start by plotting the intercept $(0,b)$. Then, we can pick another point by going right 1 unit and up $m$ units. For example, to plot the line $y=-5x+2$, we can start at the intercept $(0,2)$, and since the slope is $-5$, we will go right $1$ unit and down $5$ units to arrive at a second point $(1,-3)$. Then, we can connect these two points with a line.

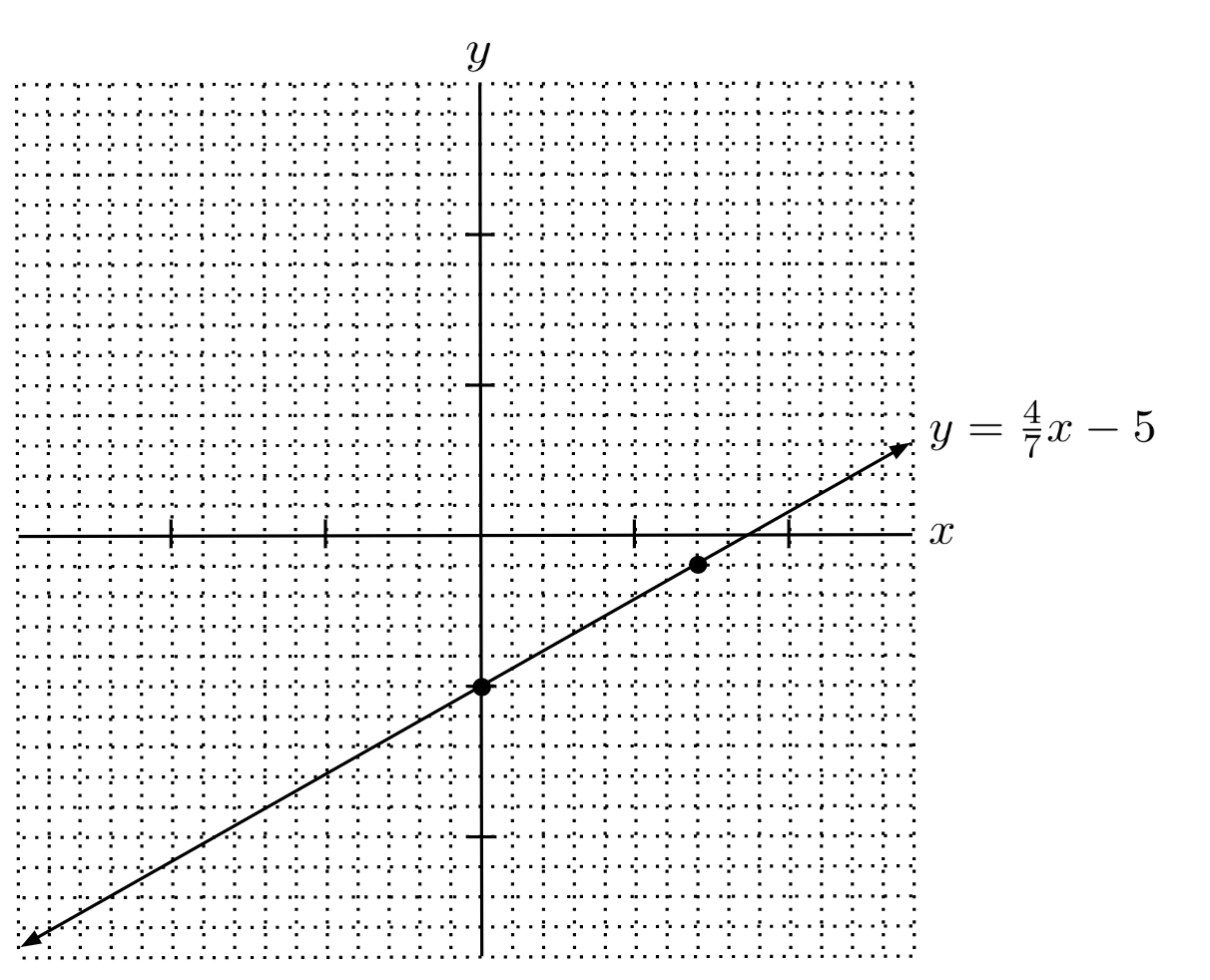
When we have a fractional slope, such as in the line $y = \frac{4}{7} x - 5$, it is easier to go right $7$ units and up $4$ units, instead of going right $1$ unit and up $\frac{4}{7}$ of a unit. We’re just repeating the process $7$ times, for a total distance right of $(1)(7)=7$ and a total distance up of $\left( \frac{4}{7} \right) (7) = 4$. The resulting line is shown in the graph below.

Horizontal and Vertical Lines

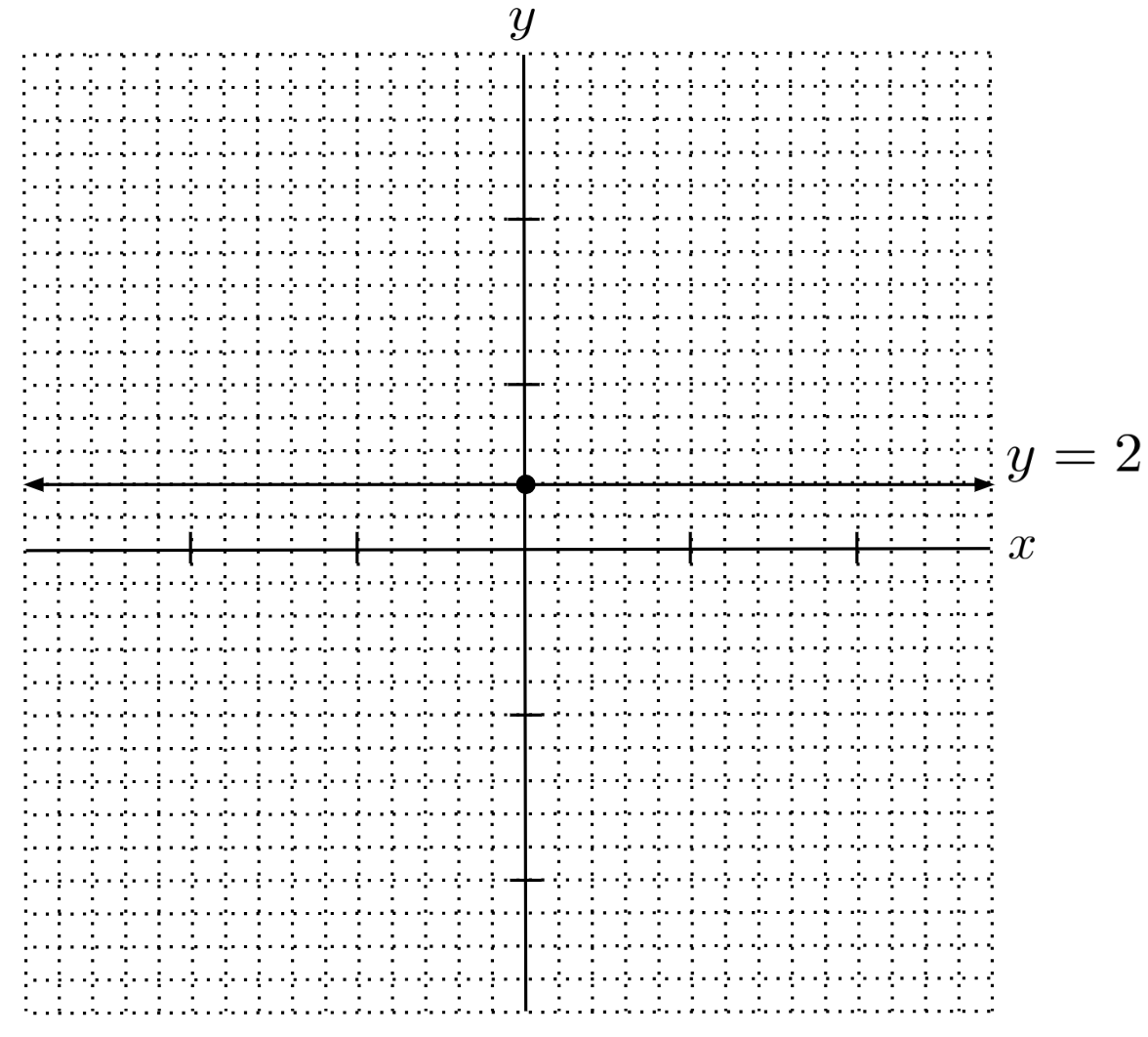
If the $x$ term vanishes when we solve for $y$, such as in the line $y+x=2+x$ which simplifies to $y=2$, then we can interpret the slope as being $0$ because the line can be written $y=0x+2$. The resulting line has a y-intercept $(0,2)$ and is horizontal because for every unit it goes to the right, it goes $0$ units up.

Perhaps an easier way to think about it, though, is that the solution is just all the points that have a y-coordinate of $2$, regardless of their x-coordinates.

On the other hand, if $y$ vanishes when we solve, such as in the line $y-x=y+3$ which simplifies to $x=-3$, then we have a vertical line that passes through all the points having an x-coordinate of $-3$, regardless of their y-coordinate.

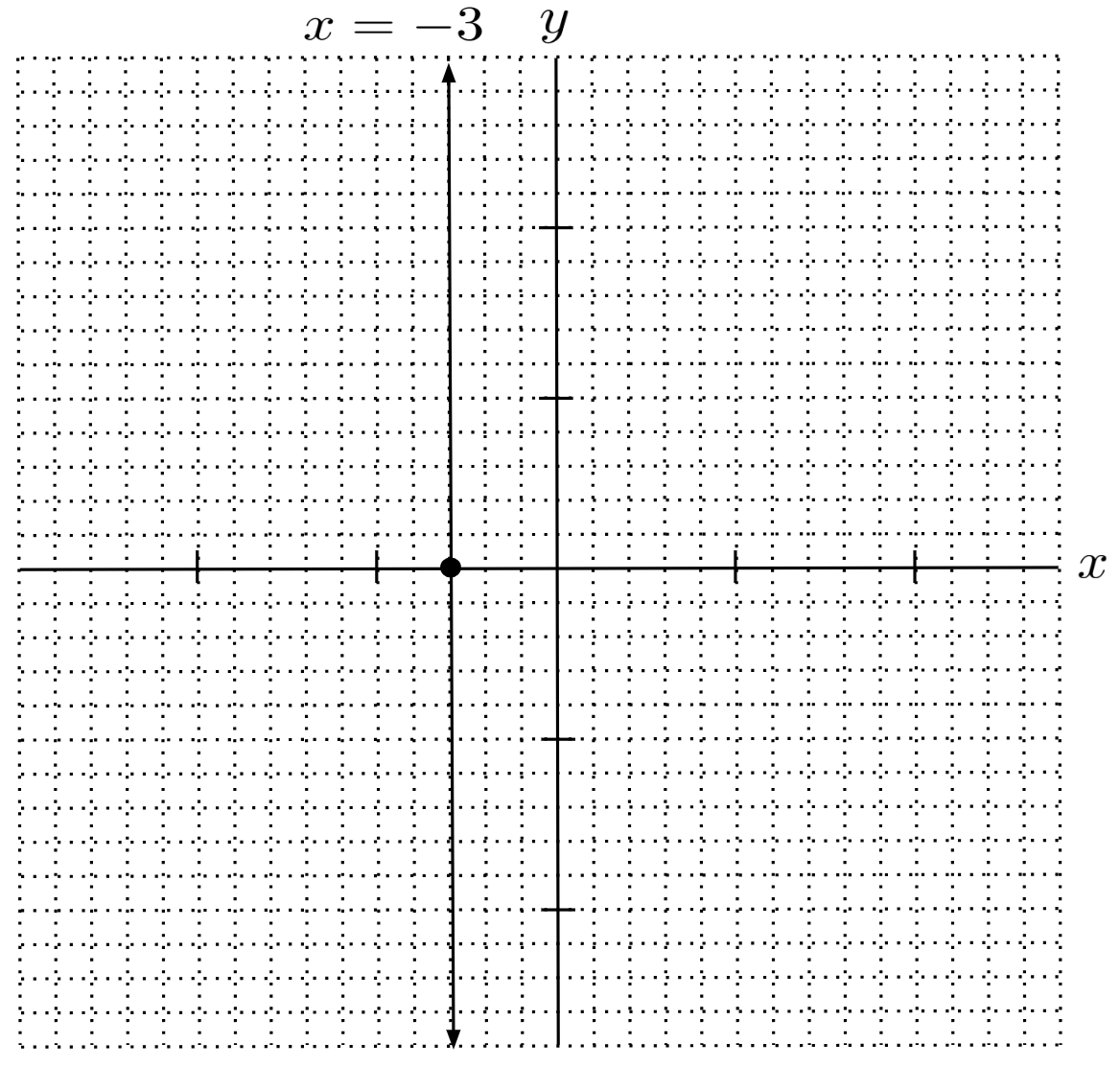
Finding the Equation from a Graph

Now, let’s think in reverse: if we draw a particular line, how can we come up with its equation?

If we know the y-intercept and slope of the line, then it’s easy – we just substitute the slope for $m$ and the y-intercept for $b$ in the equation $y=mx+b$.

For example, in the line below, we see that the y-intercept is $-6$, and when we go right $3$, we go up $2$, so the slope is $\frac{2}{3}$. The equation of the line, then, is $y=\frac{2}{3}x - 6$.

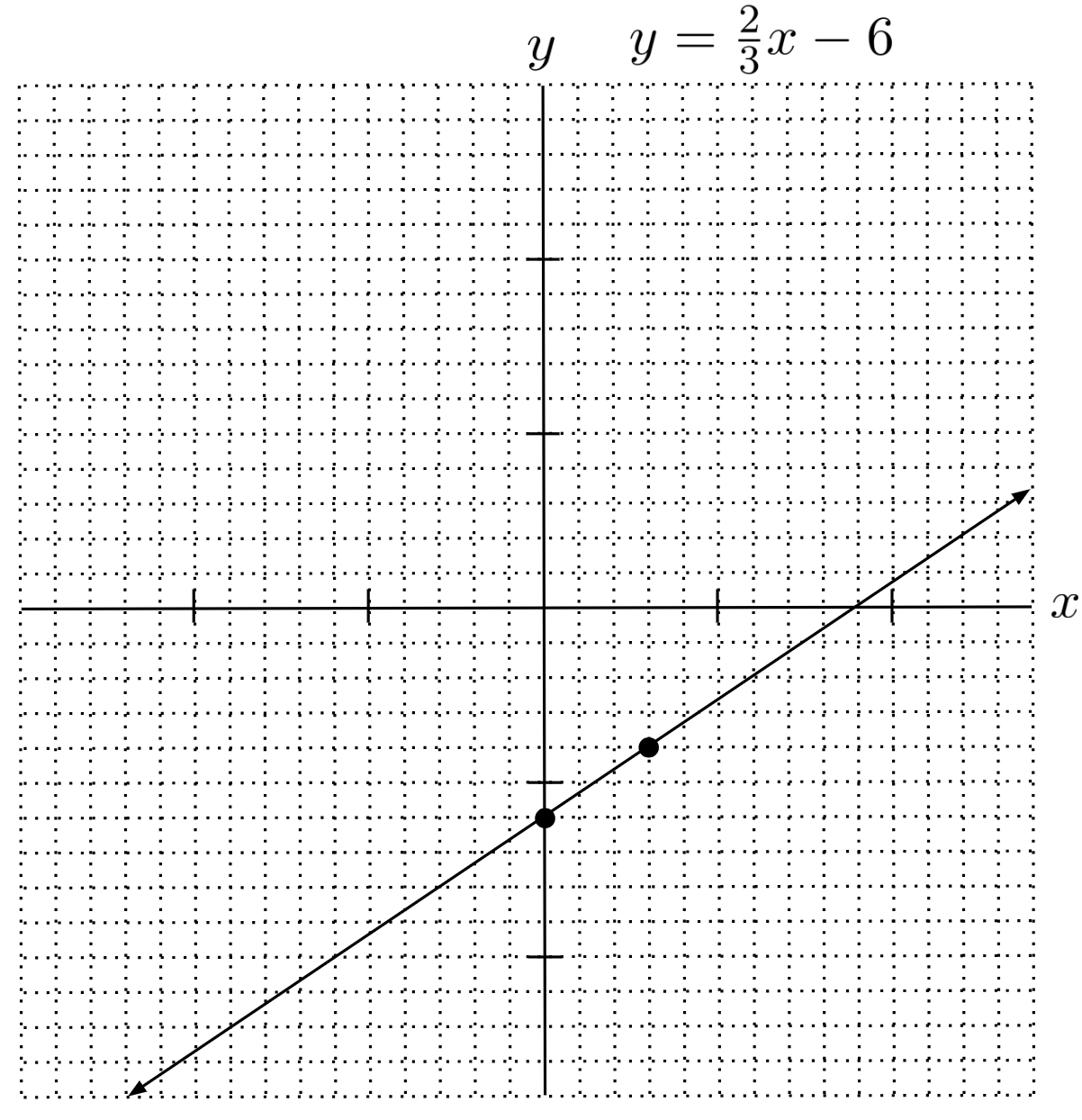
But what if we aren’t given the slope and y-intercept, or even a picture of the line, and we want to write the equation of the line based on only two points it passes through?

It’s straightforward to compute the slope based on the two points – we just need to find the rise, or the change in $y$, and divide it by the run, or the change in $x$.

For example, if the points are $(-10,3)$ and $(5,2)$, then we can compute the rise as $2-3=-1$ and the run as $5-(-10)=15$, resulting in a slope of $m = \frac{-1}{15} = - \frac{1}{15}$.

Or, we can compute the rise as $3-2=1$ and the run as $-10-5=-15$, still resulting in a slope of $m = \frac{1}{-15} = -\frac{1}{15}$.

Either way, we get the same slope.

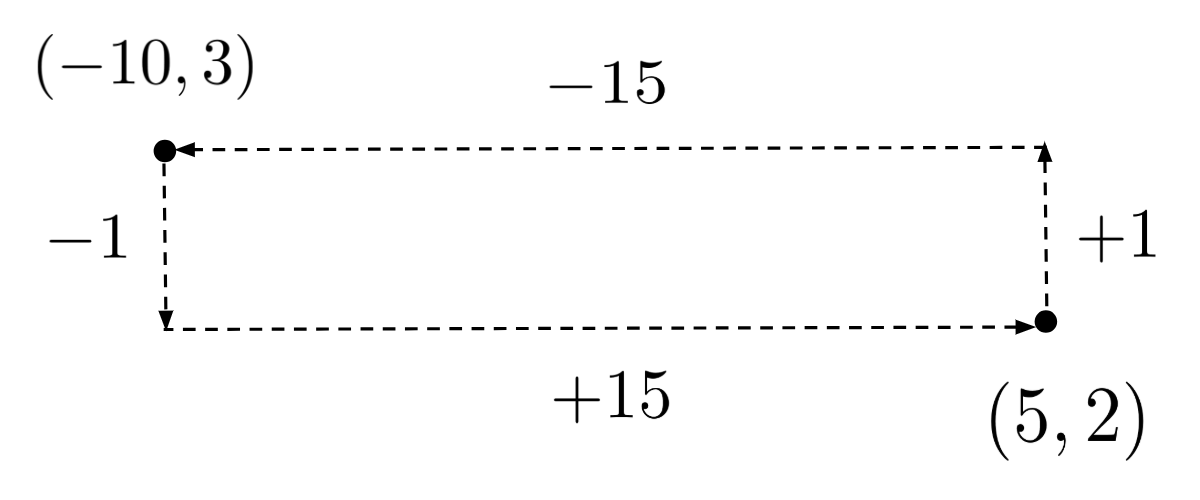
Substituting for $m$ in the equation $y=mx+b$, we reach

It remains to find the y-intercept, $b$. We can do this by substituting for $x$ and $y$ using the coordinates of one of the points that we know needs to be on the line, say, $(5,2)$.

It really doesn’t matter which point we use – even if we used the other point, $(-10,3)$, we would get the same result for $b$.

Now that we know the y-intercept is $b = \frac{7}{3}$, we can write the final equation of the line:

Exercises

Graph the following linear equations. (You can view the solution by clicking on the problem.)

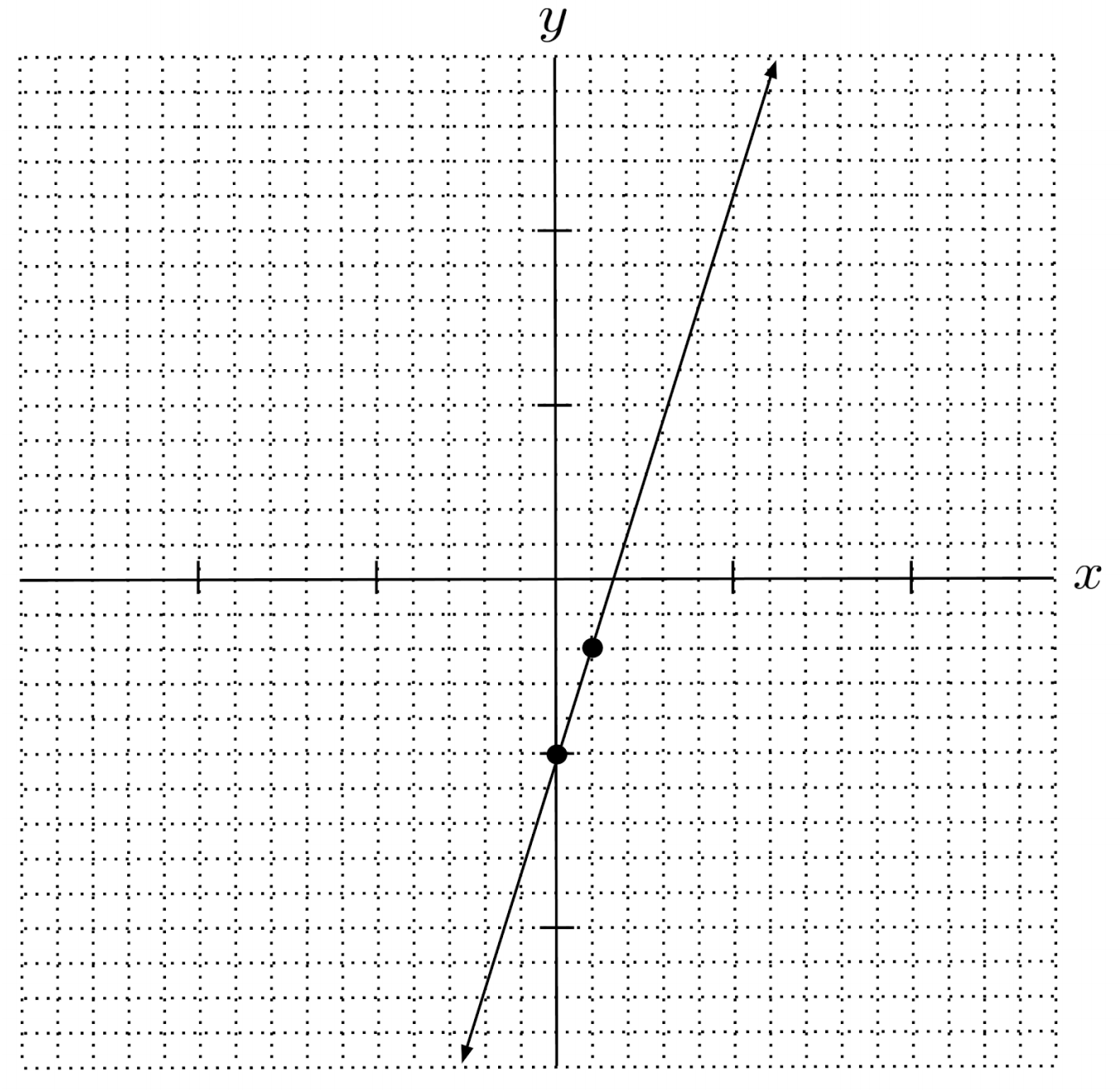
$1) \hspace{.5cm} y = 3x - 5$

Solution:

$2) \hspace{.5cm} y = -4x + 6$

Solution:

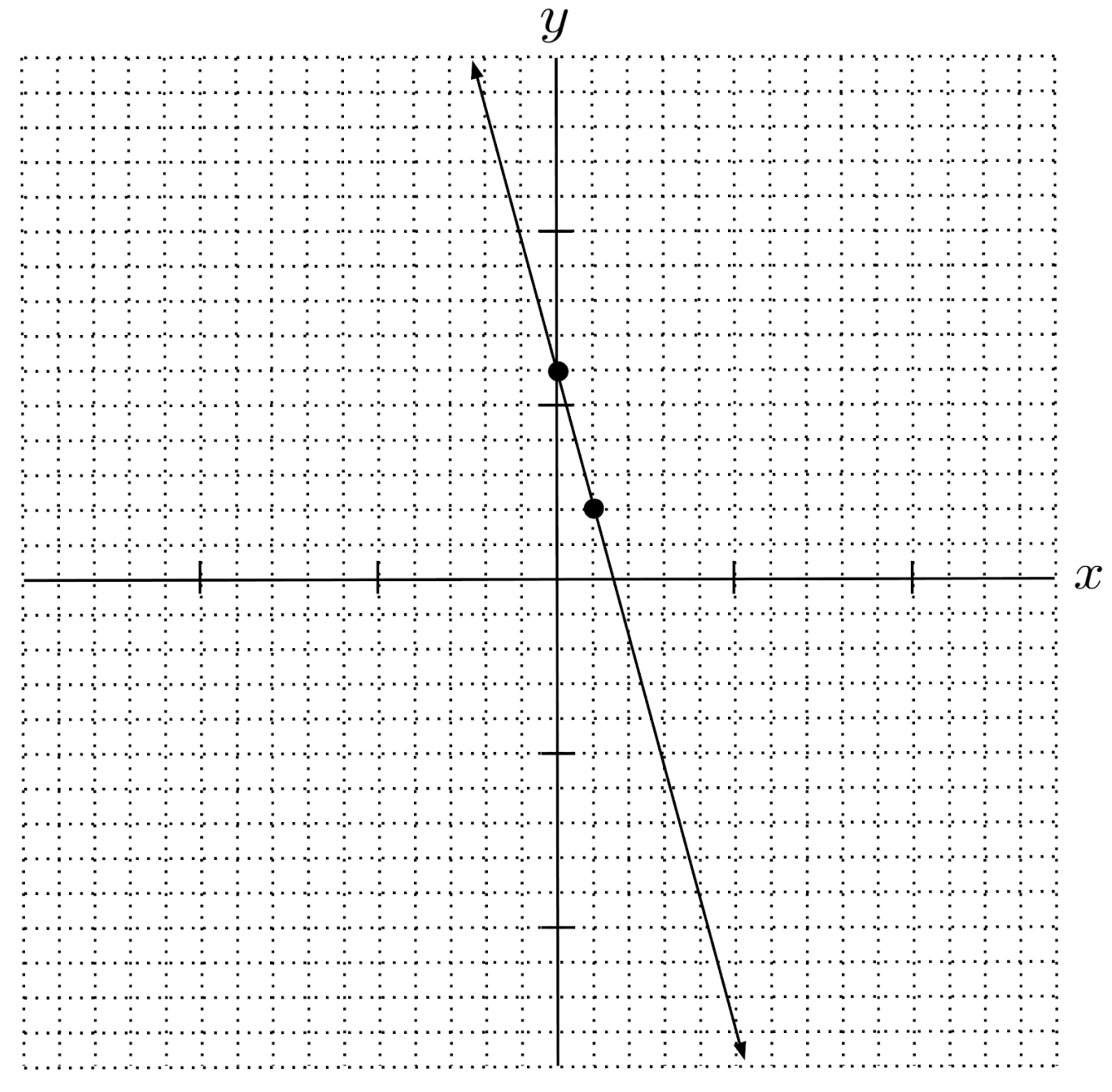
$3) \hspace{.5cm} y = \frac{3}{5} x + 2$

Solution:

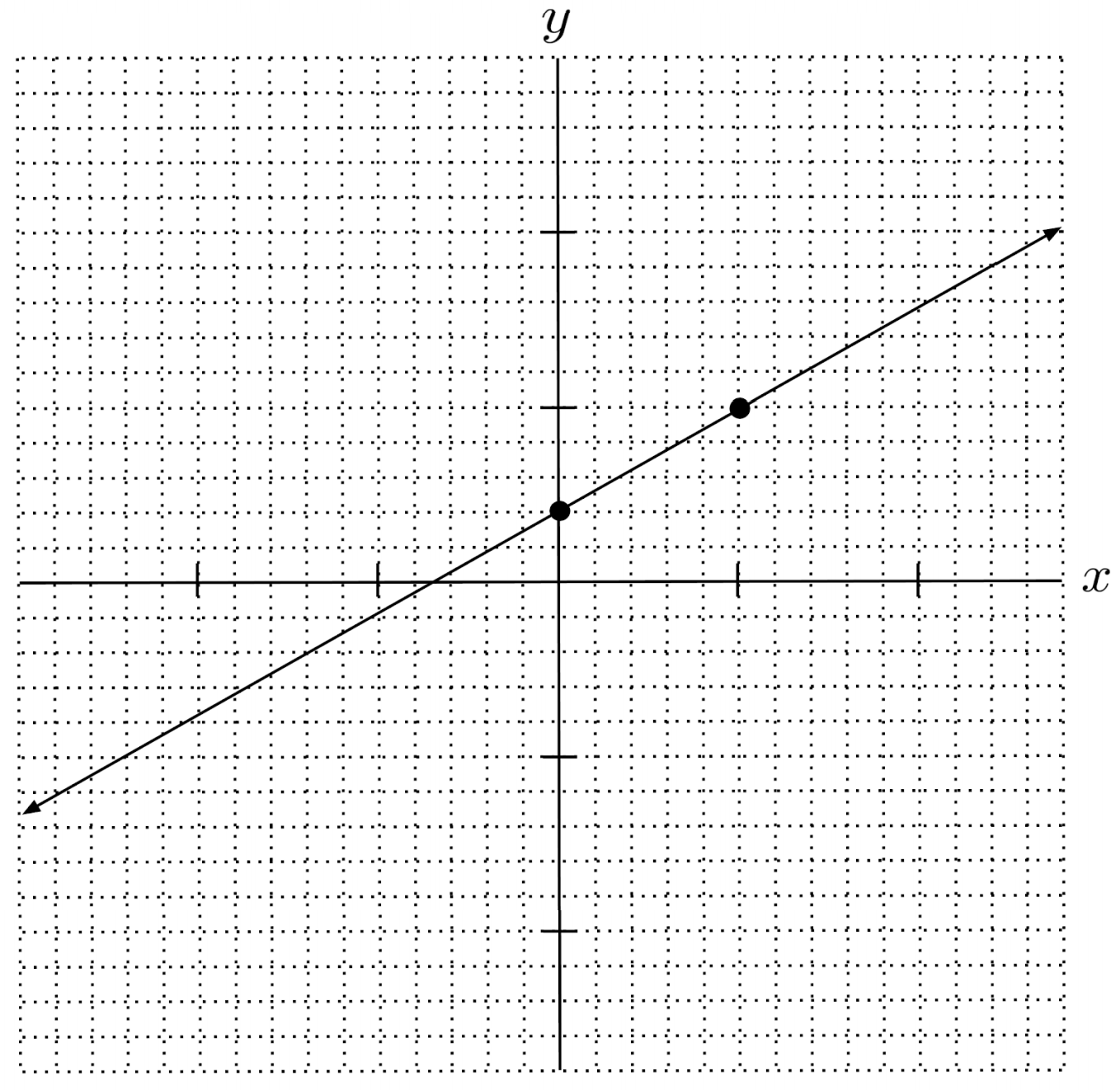
$4) \hspace{.5cm} y = 4 - \frac{2}{7} x$

Solution:

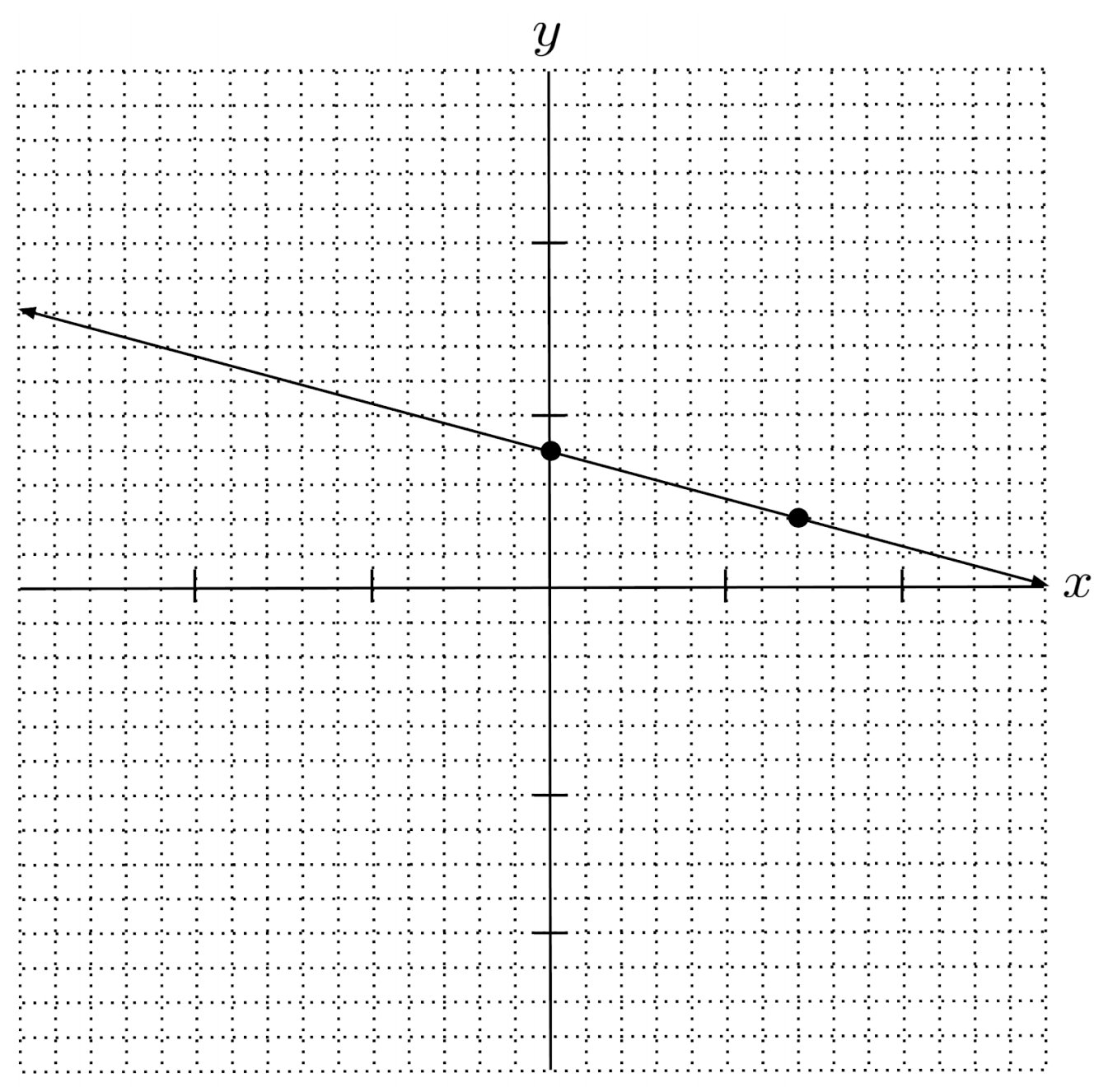
$5) \hspace{.5cm} 8y = 16 - 4x$

Solution:

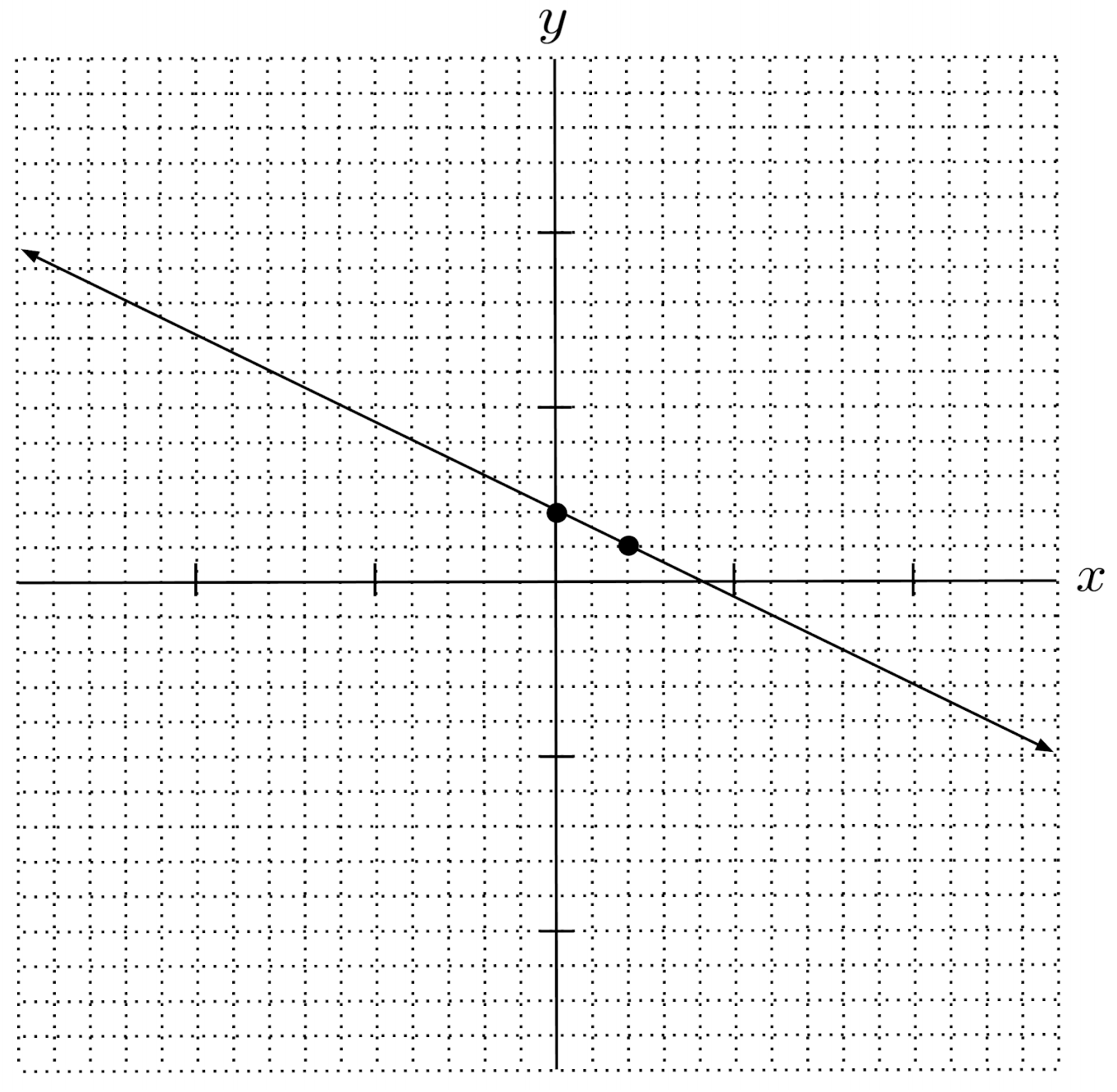
$6) \hspace{.5cm} 2x = 2(x+y) + 1$

Solution:

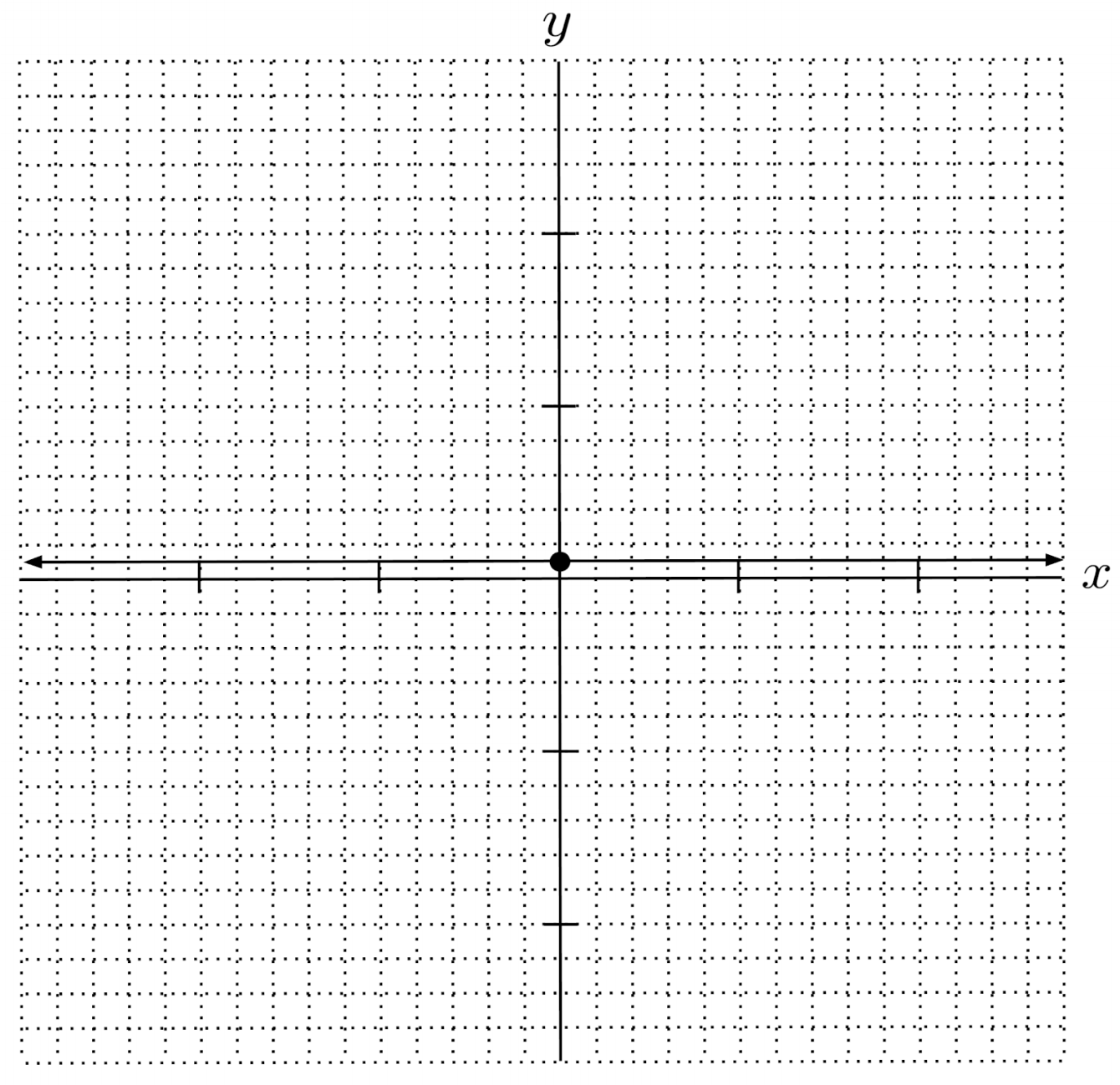
$7) \hspace{.5cm} 4x+10 = 2(x+2y) $

Solution:

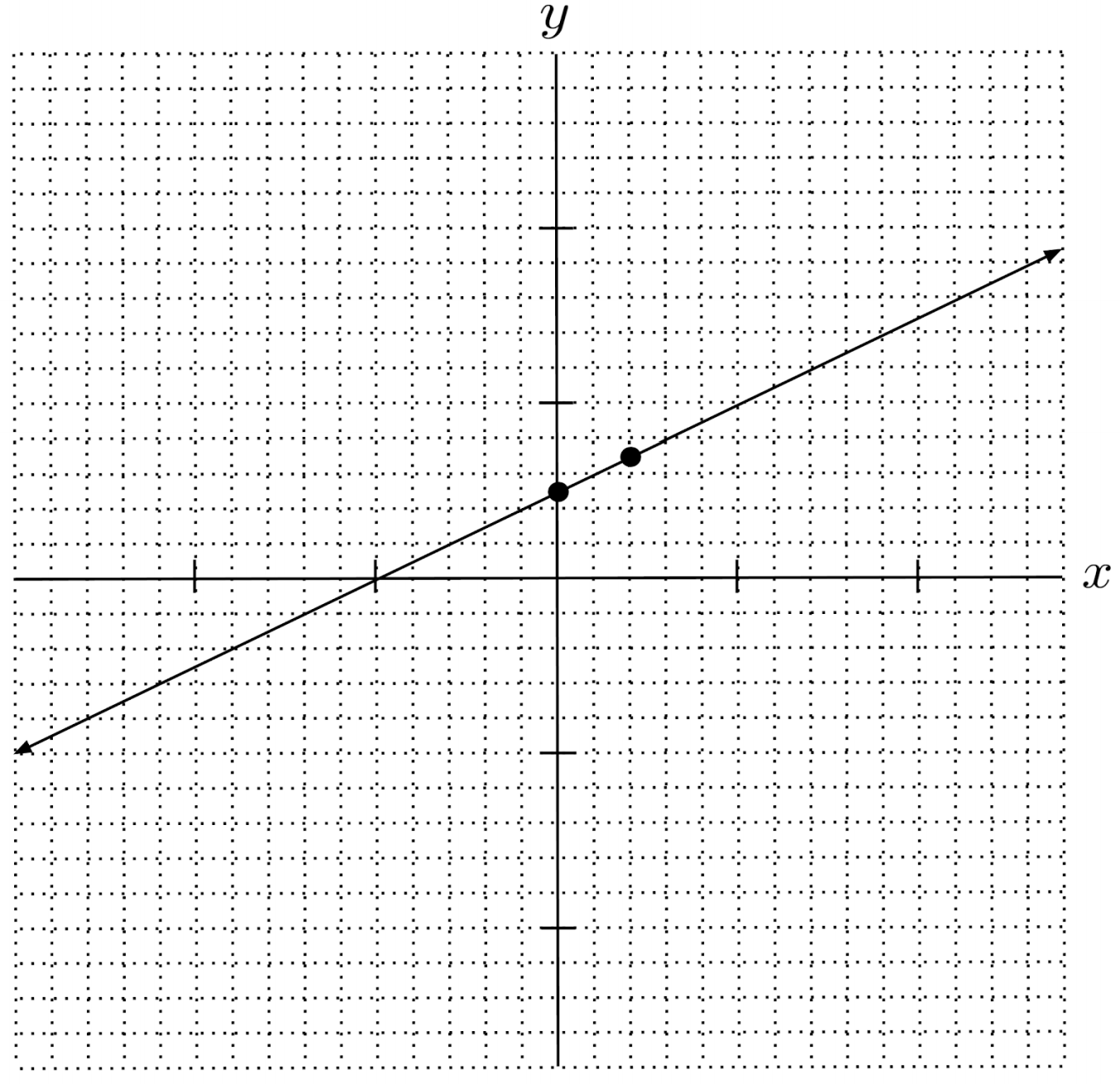
$8) \hspace{.5cm} 2(1-y)=8(x-2)$

Solution:

Write the equation of the line in slope-intercept form. (You can view the solution by clicking on the problem.)

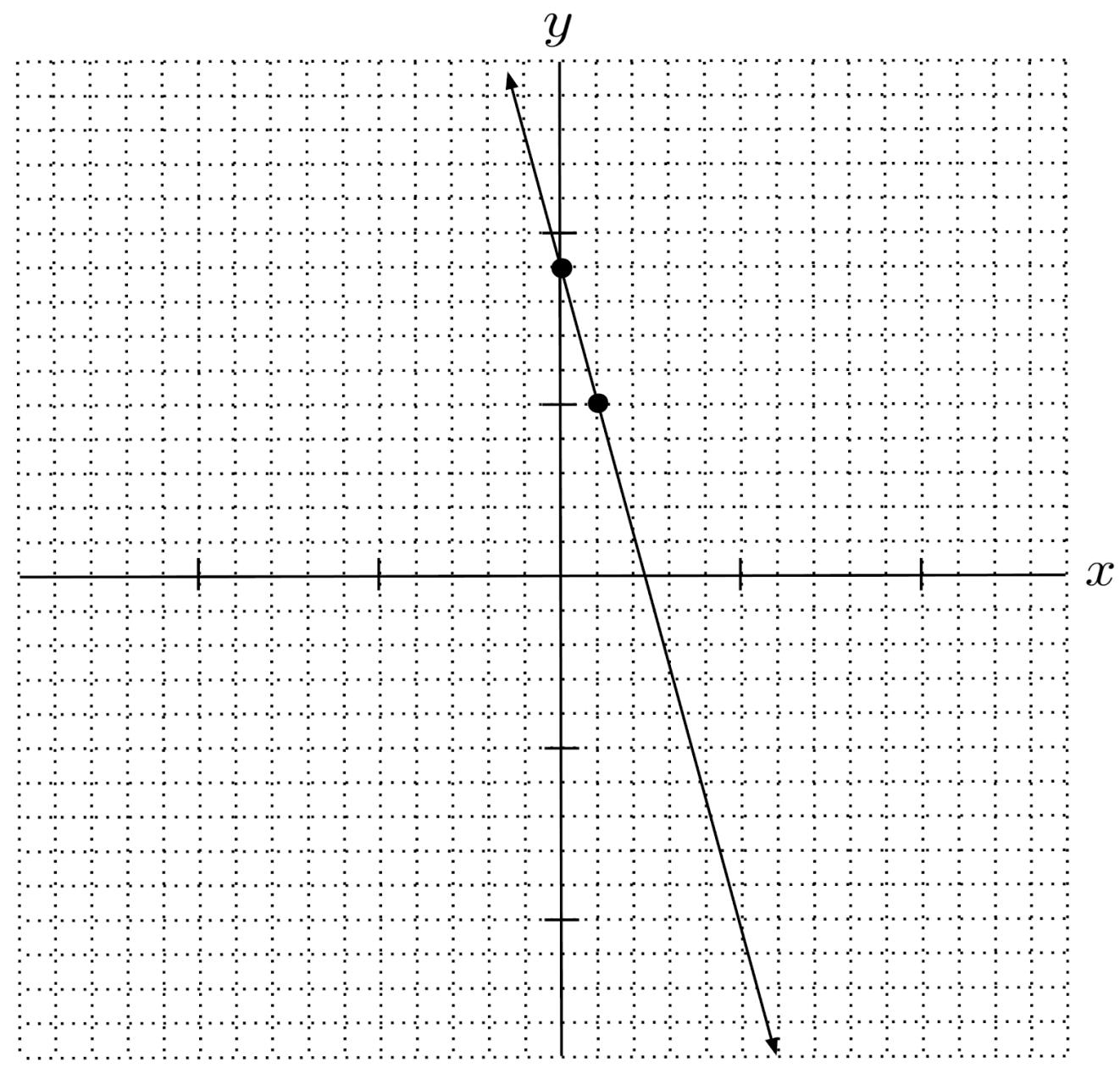
$9) \hspace{.5cm}$

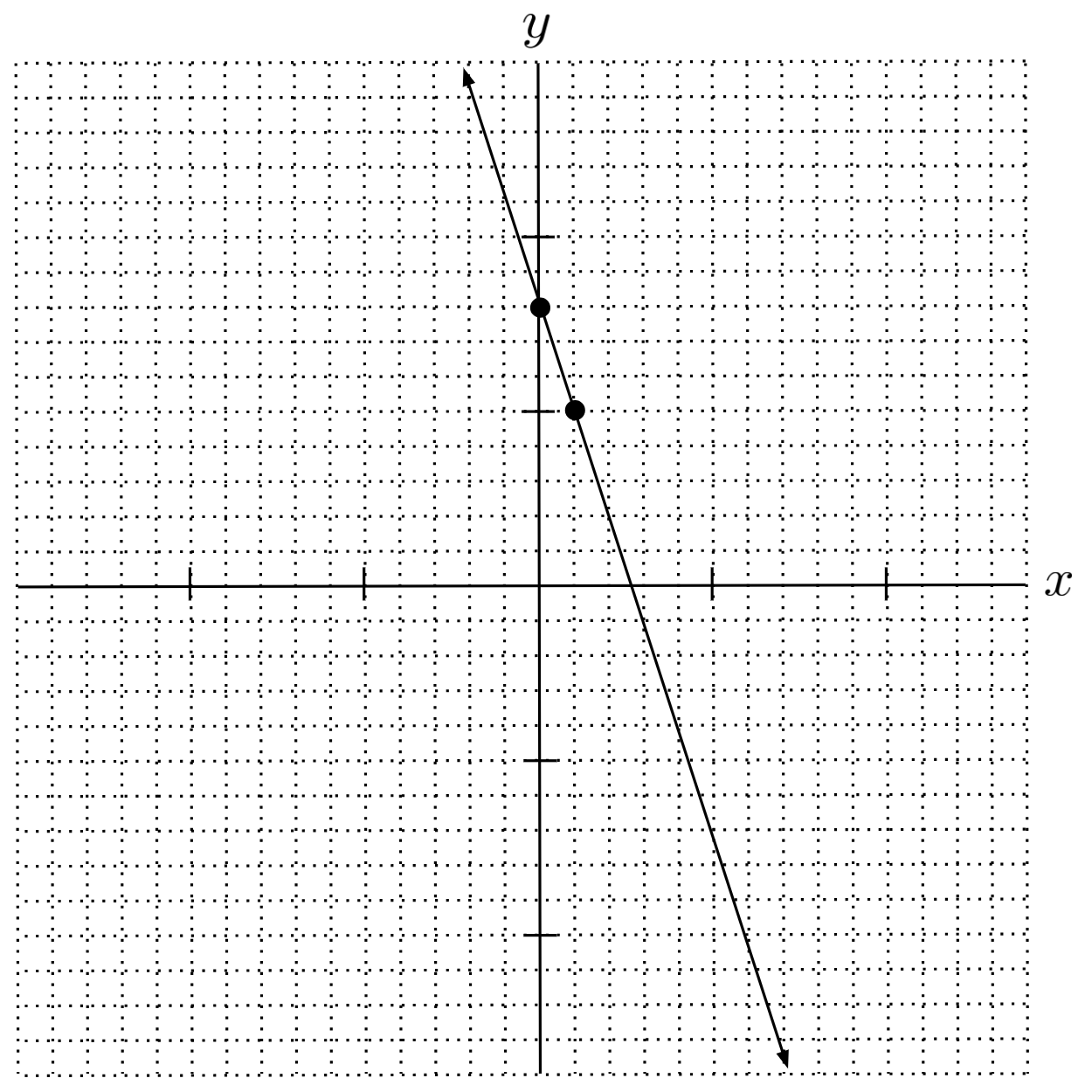
Solution:
$y=-3x+8$

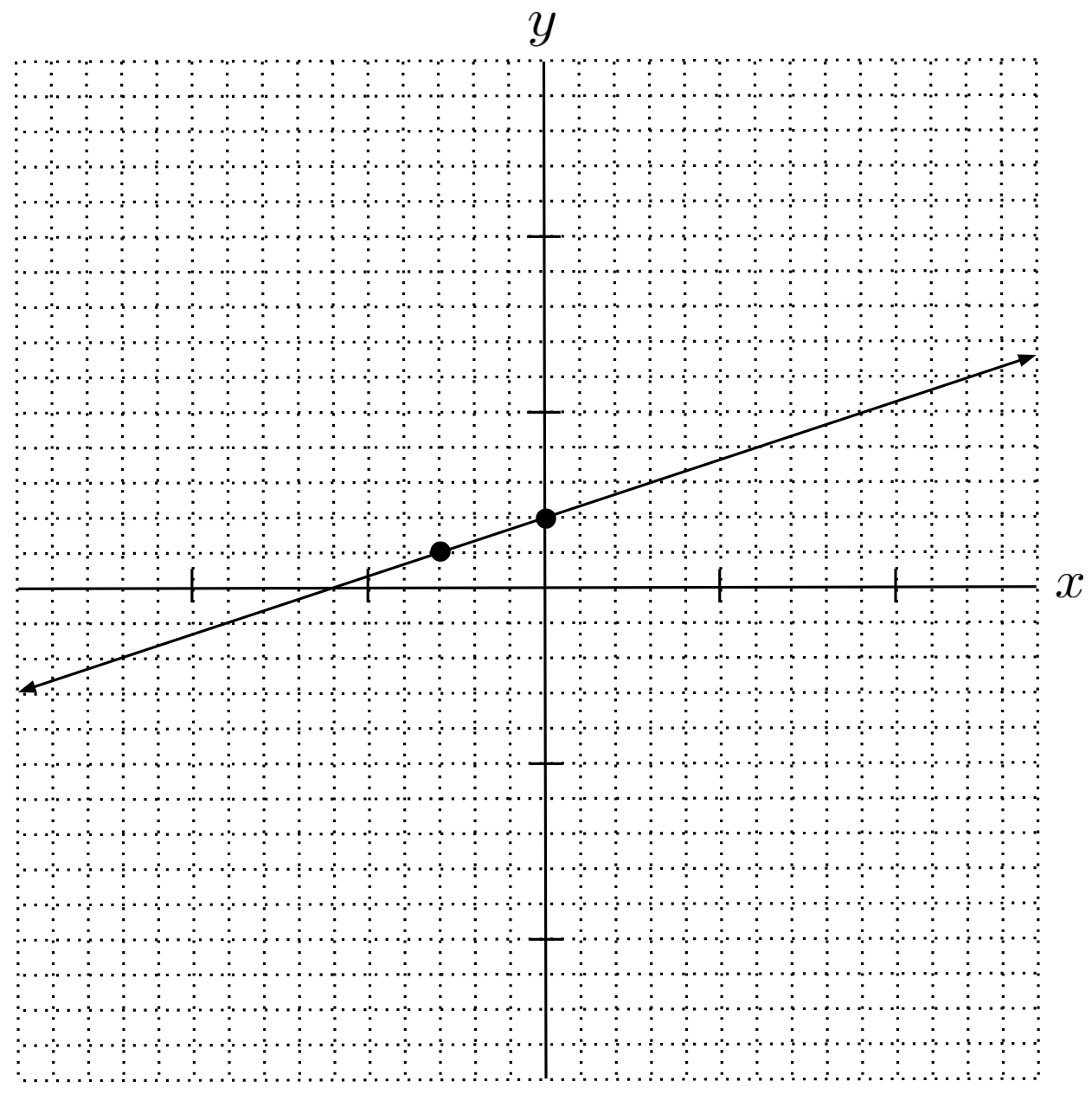
$10) \hspace{.5cm}$

Solution:
$y=\frac{1}{3}x+2$

$11) \hspace{.5cm}$

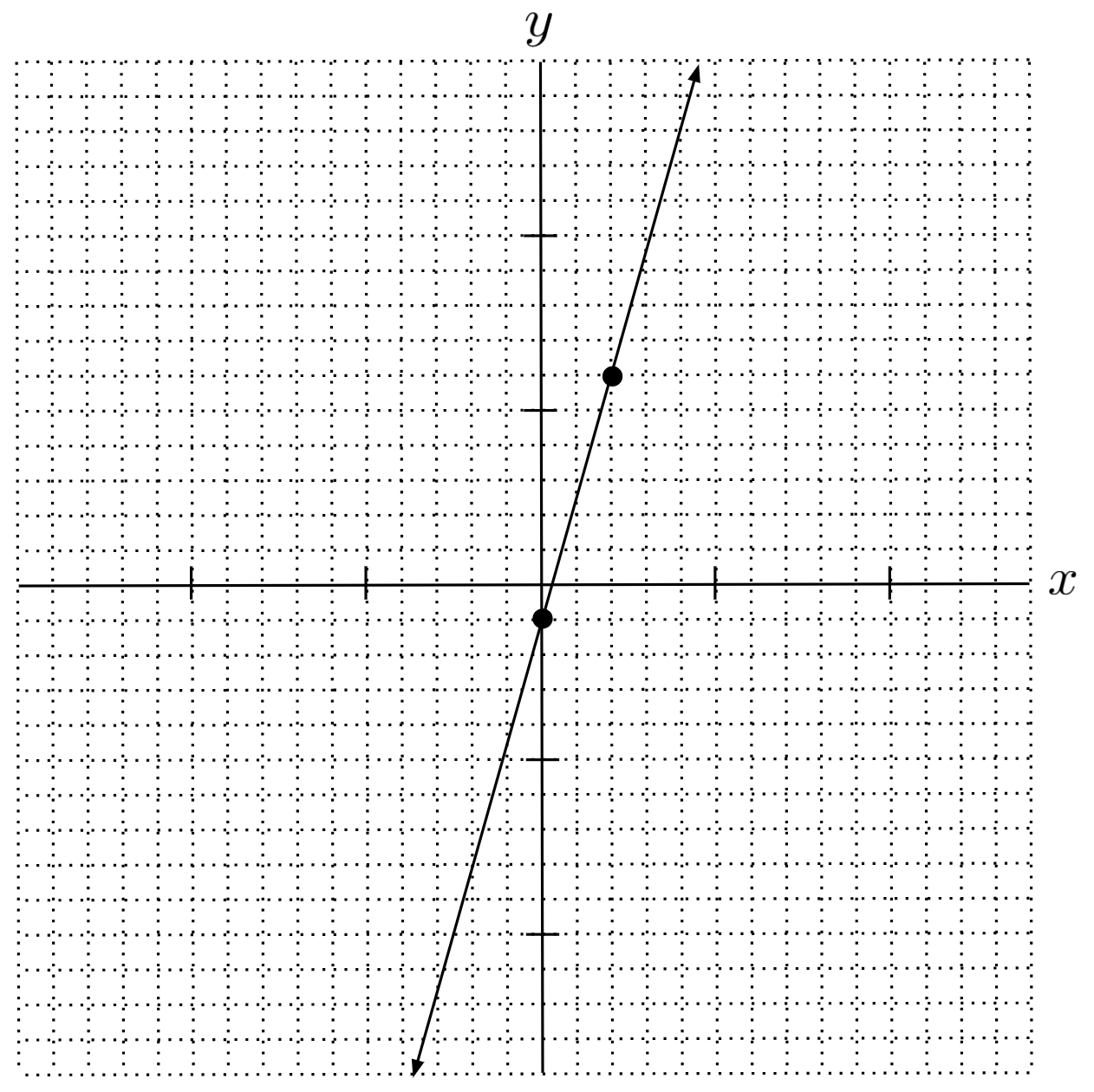
Solution:
$y=\frac{7}{2}x-1$

$12) \hspace{.5cm}$

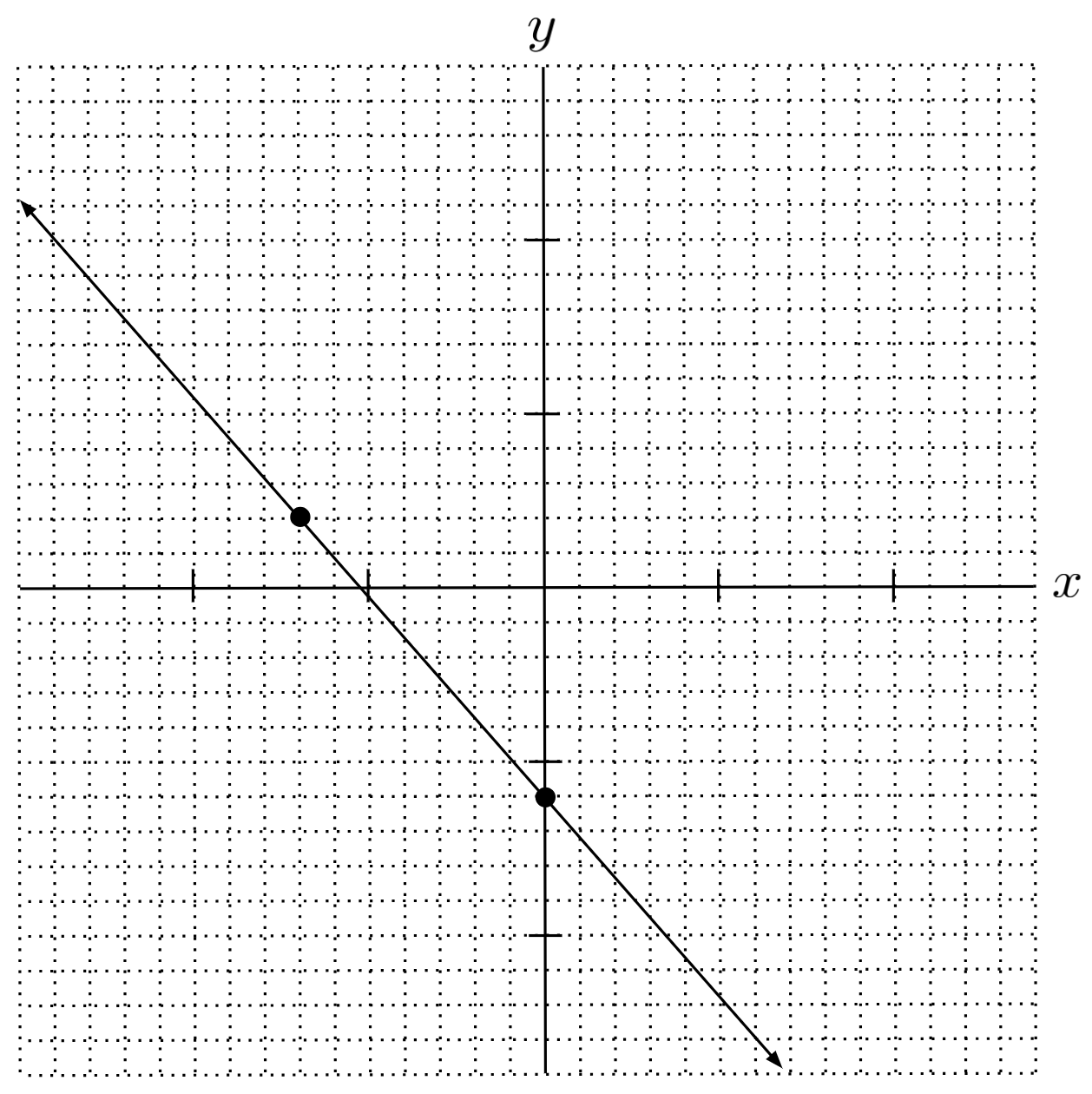
Solution:
$y=-\frac{8}{7}x-6$

Write the slope-intercept equation of the line that goes through the given point, with the given slope. (You can view the solution by clicking on the problem.)

Write the slope-intercept equation of the line that goes through the given points. (You can view the solution by clicking on the problem.)

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Slope-Intercept Form. In Justin Math: Algebra. https://justinmath.com/slope-intercept-form/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.