Single-Variable Gradient Descent

by Justin Skycak (@justinskycak) on February 04, 2021

We take an initial guess as to what the minimum is, and then repeatedly use the gradient to nudge that guess further and further "downhill" into an actual minimum.

This post is part of the book Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. Suggested citation: Skycak, J. (2021). Single-Variable Gradient Descent. In Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. https://justinmath.com/single-variable-gradient-descent/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Gradient descent is a technique for minimizing differentiable functions. The idea is that we take an initial guess as to what the minimum is, and then repeatedly use the gradient to nudge that guess further and further “downhill” into an actual minimum.

Let’s start by considering the simple case of minimizing a single-variable function – say, $f(x) = x^2$ with the initial guess that the minimum is at $x=1.$ Of course, this guess is not correct since the minimum is not actually at $x=1,$ but we will repeatedly update the guess to become more and more correct.

Intuition About the Sign of the Derivative

To update our guess, we start by computing the gradient at $x=1.$ For a single-variable function, the gradient is just the plain old derivative.

$\begin{align*} f(x) &= x^2 \\ f'(x) &= 2x \\ f'(1) &= 2 \cdot 1 = 2 \end{align*}$

We found that the derivative is $f’(1) = 2.$ Now that we know the value of the derivative at our guess, we can use it to update our guess. In general, we have the following intuition:

If the derivative is positive, then the function is sloping up, and we can move downhill by nudging our guess to the left (i.e. decreasing the $x$-value of our guess).
If the derivative is negative, then the function is sloping down, and we can move downhill by nudging our guess to the right (i.e. increasing our the $x$-value of our guess).

Put more simply:

If the function is increasing, then we should decrease our guess.
If the function is decreasing, then we should increase our guess.

Here, the derivative $f’(1) = 2$ is positive, which means the function is increasing and we should decrease the $x$-value of our guess. Indeed, if we sketch up a graph of the situation, we can see that decreasing our guess will take us closer to the actual minimum:

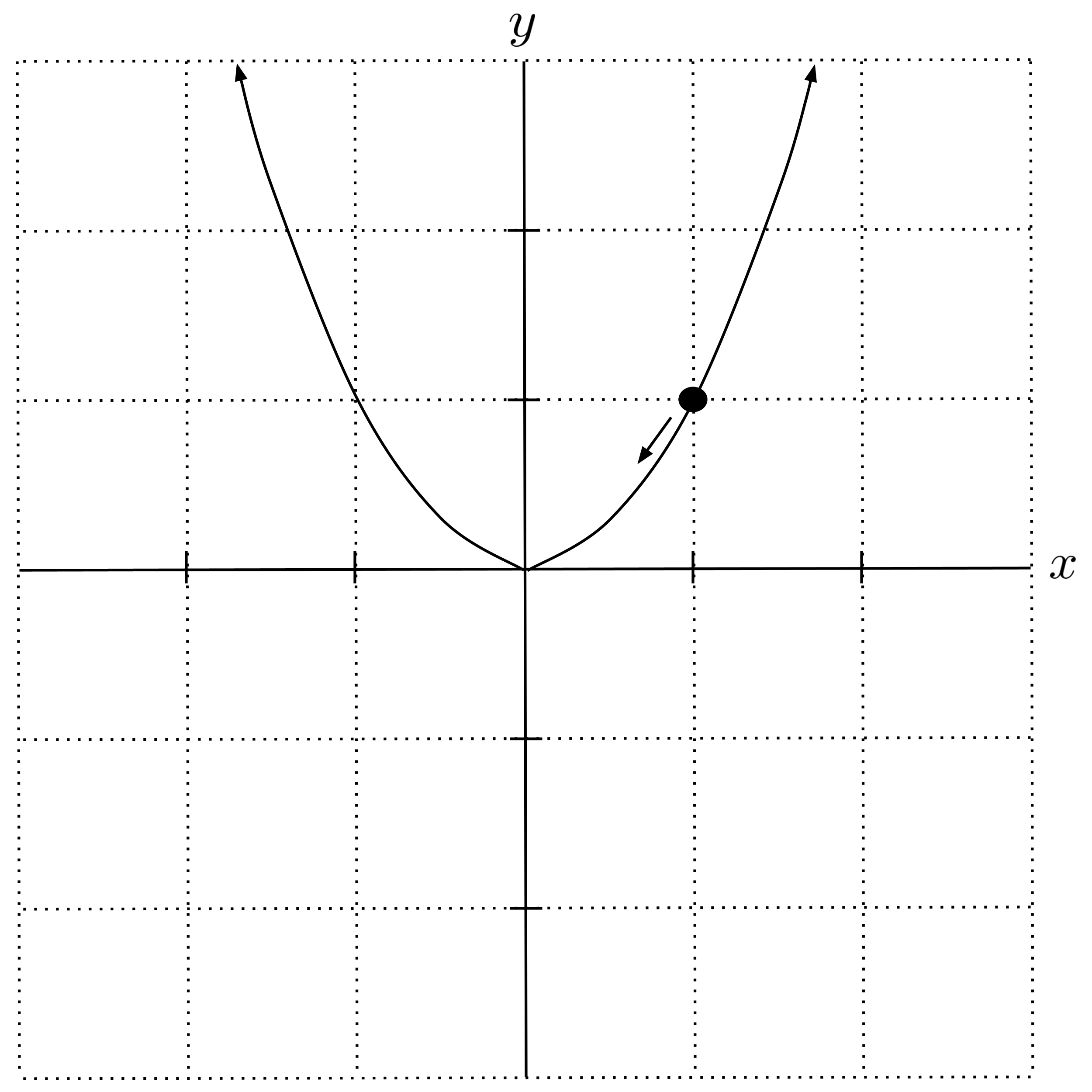
Gradient Descent Formula

Now, the question is: by how much should we update our guess? If we decrease the $x$-value of our guess by too much, then we’ll pass right over the minimum and end up on the other side, maybe even further away from the minimum than we were to start with. But if we decrease the $x$-value of our guess by too little, then we will barely move at all and we will have to repeat this procedure an excessive number of times before actually getting close to the minimum.

For most differentiable functions that appear in machine learning, the amount by which we should update our guess depends on how steep the graph is. The steeper the graph is, the further we are from the minimum, and the more freedom we have to update our guess without worrying about moving it too far. So, we have the following formula for our next guess:

$\begin{align*} x_{n+1} = x_n - \alpha f'(x_n) \end{align*}$

Before we perform any computations with this formula, let’s elaborate on each part of it.

$x_n$ is our $n$th guess (i.e. the current guess), and $x_{n+1}$ is the next guess.
$f'(x_n)$ is the derivative at our current guess, and it tells us whether the function is increasing or decreasing (as well as how steep the function is).
$\alpha$ is a positive constant called the learning rate, and the quantity $\alpha f'(x_n)$ is the amount by which we update our guess. (We generally try to run the gradient descent algorithm with a learning rate around $\alpha \approx 0.01$ to start with, but if this learning rate causes our guesses to diverge, then decrease the learning rate and try again. More on that later.)
We are subtracting $\alpha f'(x_n)$ because we want to move our guess $x_n$ in the opposite direction as the derivative $f'(x_n)$. Remember that if the function is increasing (i.e. positive derivative) then we want to move our guess to the left (i.e. decrease it), and if the function is decreasing (i.e. negative derivative) then we want to move our guess to the right (i.e. increase it). The steeper the graph is (i.e. the larger the magnitude of the derivative), the further we want to move our guess.

Worked Example

Now, let’s finish working out our example. We are trying to minimize the function $f(x) = x^2,$ our first guess is $x_0 = 1,$ and the derivative at this guess is $f’(1) = 2.$ If we use a learning rate of $\alpha = 0.01,$ then our next guess is

$\begin{align*} x_{1} &= x_0 - \alpha f'(x_0) \\ &= 1 - (0.01) \, f'(1) \\ &= 1 - (0.01) (2) \\ &= 0.98. \end{align*}$

To get the guess after that, we simply repeat the procedure again:

$\begin{align*} x_{2} &= x_1 - \alpha f'(x_1) \\ &= 0.98 - (0.01) \, f'(0.98) \\ &= 0.98 - (0.01) (1.96) \\ &= 0.9604 \end{align*}$

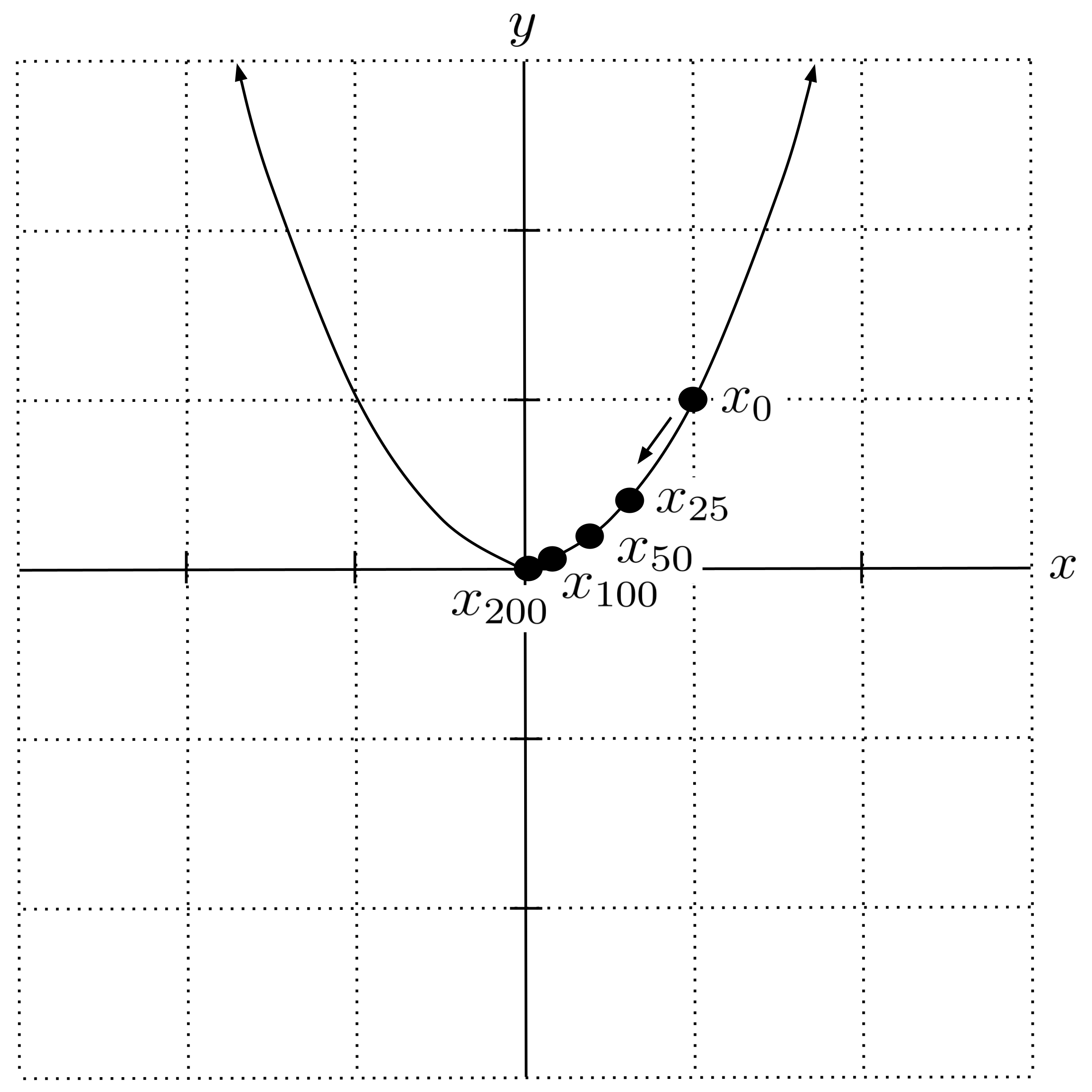
In practice, we usually implement gradient descent as a computer program because it is extremely tedious to do by hand. You should do this and verify that you get the same results as shown in the table below. In the table, we will round to $6$ decimal places (but we do not actually round in our computer program).

$\begin{align*} \begin{matrix} n & x_n & f'(x_n) & \alpha f'(x_n) \\ \hline 0 & 1 & 2 & 0.02 \\ 1 & 0.98 & 1.96 & 0.0196 \\ 2 & 0.9604 & 1.9208 & 0.019208 \\ 3 & 0.941192 & 1.882384 & 0.018824 \\ \vdots & \vdots & \vdots & \vdots \\ 25 & 0.603465 & 1.206929 & 0.012069 \\ 50 & 0.364170 & 0.728339 & 0.007283 \\ 100 & 0.132620 & 0.265239 & 0.002652 \\ 200 & 0.017588 & 0.035176 & 0.000352 \\ 300 & 0.002333 & 0.004665 & 0.000047 \\ 400 & 0.000309 & 0.000619 & 0.000006 \end{matrix} \end{align*}$

We can visualize these results on our graph. Indeed, we see that our guesses are converging to the minimum at $x=0.$

Local vs Global Minima

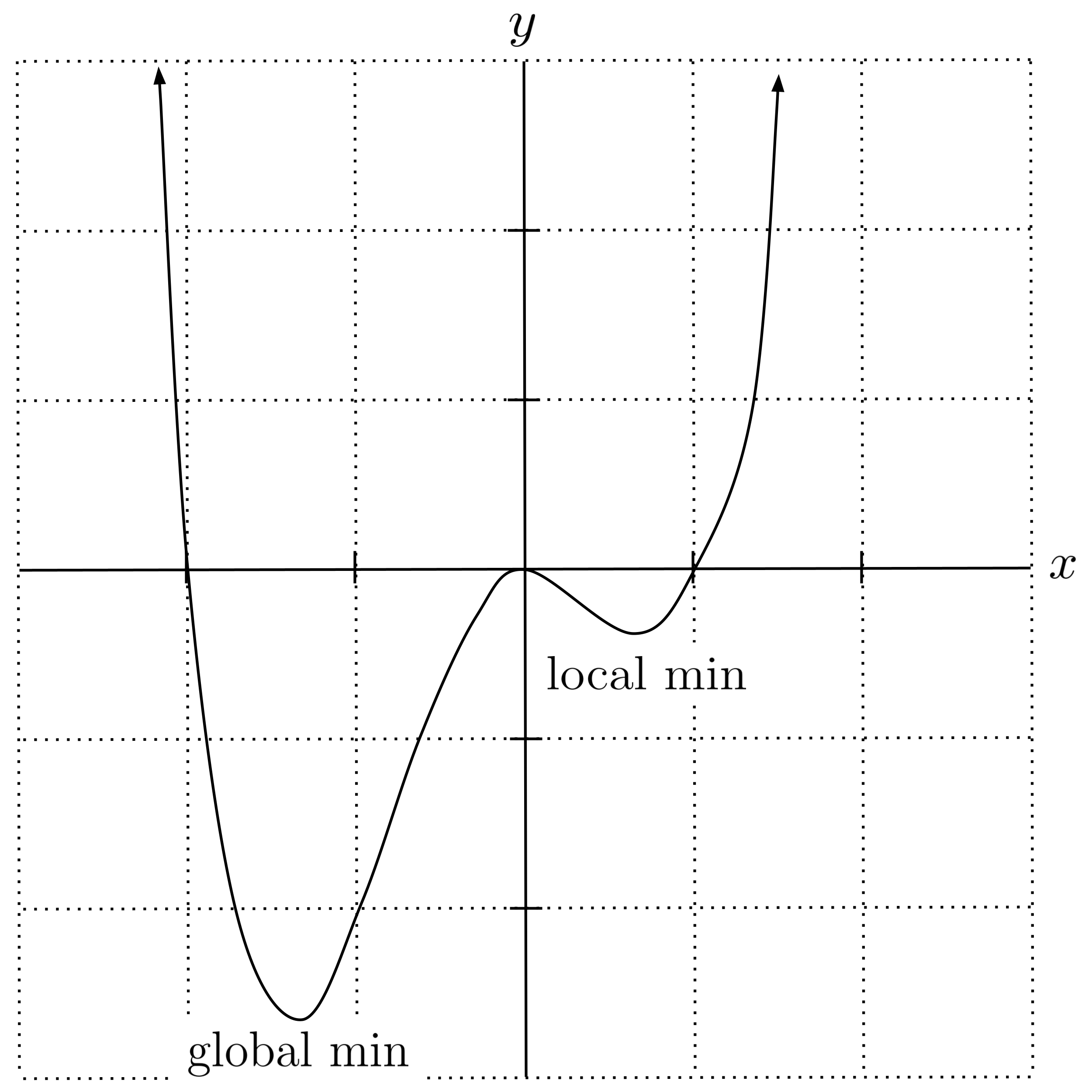
There is one big caveat to gradient descent that is essential to understand: it is not guaranteed to converge to a global minimum. It’s possible for gradient descent to get “stuck” in a local minimum, just like a ball rolling down a hill might roll into a depression and get stuck there instead of falling all the way to the bottom of the hill.

To illustrate this caveat numerically, let’s use gradient descent to find the minimum value of the function $f(x) = x^{4}+x^{3}-2x^{2}$ starting with the initial guess $x=1.$ Note that the derivative of this function is $f’(x) = 4x^3 + 3x^2 - 4x.$

$\begin{align*} \begin{matrix} n & x_n & f'(x_n) & \alpha f'(x_n) \\ \hline 0 & 1 & 3 & 0.03 \\ 1 & 0.97 & 2.593392 & 0.025934 \\ 2 & 0.944066 & 2.263154 & 0.022632 \\ 3 & 0.921435 & 1.990732 & 0.019907 \\ \vdots & \vdots & \vdots & \vdots \\ 25 & 0.736701 & 0.280693 & 0.002807 \\ 50 & 0.701878 & 0.053456 & 0.000535 \\ 100 & 0.693413 & 0.002445 & 0.000024 \\ 200 & 0.6930014 & 0.000005 & 0.000000 \end{matrix} \end{align*}$

Uh oh! We are converging to the local minimum at $x=0.69,$ but this is not the global minimum of the function.

Trying Different Initial Guesses

Because it’s possible for gradient descent to get stuck in local minima, it’s often a good idea to run the gradient descent procedure with several different initial guesses and use whichever final guess gives the best result (i.e. lowest function value).

To illustrate, let’s run the gradient descent algorithm a couple more times with different initial guesses. For the next run, we’ll start with the initial guess $x=0.$

$\begin{align*} \begin{matrix} n & x_n & f'(x_n) & \alpha f'(x_n) \\ \hline 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 \\ 3 & 0 & 0 & 0 \end{matrix} \end{align*}$

Uh oh! This is even worse. We started at the top of a hill, and the function is flat there (i.e. the derivative is zero), so our guesses are not changing at all. In other words, the ball is not rolling down the hill because it was placed at the very top where it’s flat.

Let’s try again, this time with initial guess $x=-1.$

$\begin{align*} \begin{matrix} n & x_n & f'(x_n) & \alpha f'(x_n) \\ \hline 0 & -1 & 3 & 0.03 \\ 1 & -1.03 & 2.931792 & 0.029318 \\ 2 & -1.059318 & 2.848862 & 0.028489 \\ 3 & -1.087807 & 2.752289 & 0.027523 \\ \vdots & \vdots & \vdots & \vdots \\ 25 & -1.410141 & 0.389810 & 0.003898 \\ 50 & -1.441723 & 0.015732 & 0.000157 \\ 100 & -1.442999 & 0.000022 & 0.000000 \\ 200 & -1.443000 & 0.000000 & 0.000000 \end{matrix} \end{align*}$

There we go! This time, we reached the desired global minimum.

Final Remarks

There are many different variations of gradient descent that attempt to better avoid getting stuck in local minima. For example, some variations incorporate the “momentum” of a ball rolling down a hill to help the guesses “roll through” shallow local minima, whereas other variations include random perturbations.

Additionally, there are ways to choose better initial guesses. In the example above, we did not use any particular rationale when choosing our initial guesses ($x=1, 0, -1$). But we could have (for instance) randomly generated a large number of initial guesses, plugged each one into our function $f(x),$ and only run gradient descent on those initial guesses that were associated with the lowest values of $f(x).$

Also note that it’s often necessary to try out different learning rates. In the examples above, we used a learning rate of $\alpha = 0.01$ and this worked out fine. If we had chosen a learning rate that was too high, say $\alpha = 0.5,$ then our guesses would update by too large an amount each time, causing them to jump too far and never converge. This is demonstrated below.

$\begin{align*} \begin{matrix} n & x_n & f'(x_n) & \alpha f'(x_n) \\ \hline 0 & -1 & 3 & 1.5 \\ 1 & -2.5 & -33.75 & -16.875 \\ 2 & 14.375 & 12444 & 6222 \\ 3 & -6208 & -956777563439 & -478388781719 \\ \end{matrix} \end{align*}$

On the other hand, if we had chosen a learning rate that was too low, say $\alpha = 0.000001,$ then our guesses would update by too miniscule an amount each time and we would require an excessive number of iterations to converge. This is demonstrated below.

$\begin{align*} \begin{matrix} n & x_n & f'(x_n) & \alpha f'(x_n) \\ \hline 0 & -1 & 3 & 0.000003 \\ 1 & -1.000003 & 2.999994 & 0.000003 \\ 10 & -1.000030 & 2.999940 & 0.000003 \\ 100 & -1.000300 & 2.999399 & 0.000003 \\ 1000 & -1.002997 & 2.993925 & 0.000003 \\ 10000 & -1.029675 & 2.932619 & 0.000003 \\ 100000 & -1.250157 & 1.873863 & 0.000002 \\ 1000000 & -1.442997 & 0.000046 & 0.000000 \\ \end{matrix} \end{align*}$

Lastly, note that we can maximize functions by performing gradient ascent, which is similar to gradient descent except that we replace the subtraction with addition in the update rule: $x_{n+1} = x_n + \alpha f’(x_n).$

Exercises

Use gradient descent to minimize the following functions. Before looking at the graph, perform gradient descent using several different initial guesses, and then plug your final guesses back into the function to determine which final guess is the best (i.e. gives you the lowest function value). Then, look at the graph to check whether you found the global maximum.

$f(x) = x^2 + x + 1$
$f(x) = x^3 - x^4 - x^2$
$f(x) = \dfrac{\sin x}{1+x^{2}}$
$f(x) = 3\cos x+x^{2}e^{\sin x}$

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.