Shifts of Functions

When a function is shifted, all of its points move vertically and/or horizontally by the same amount.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Shifts of Functions. In Justin Math: Algebra. https://justinmath.com/shifts-of-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

When a function is shifted, all of its points move vertically and/or horizontally by the same amount. The function’s size and shape are preserved – it is just slid in some direction, like sliding a book across a table.

Shifts Outside the Function

Shifts occur when a constant term is added in a function. When the constant term is added on the outside of a function, e.g. when $f(x)=x^2$ is transformed into $f(x)=x^2+5$, the function shifts up by that many units. (If a negative term is added, the function moves down.)

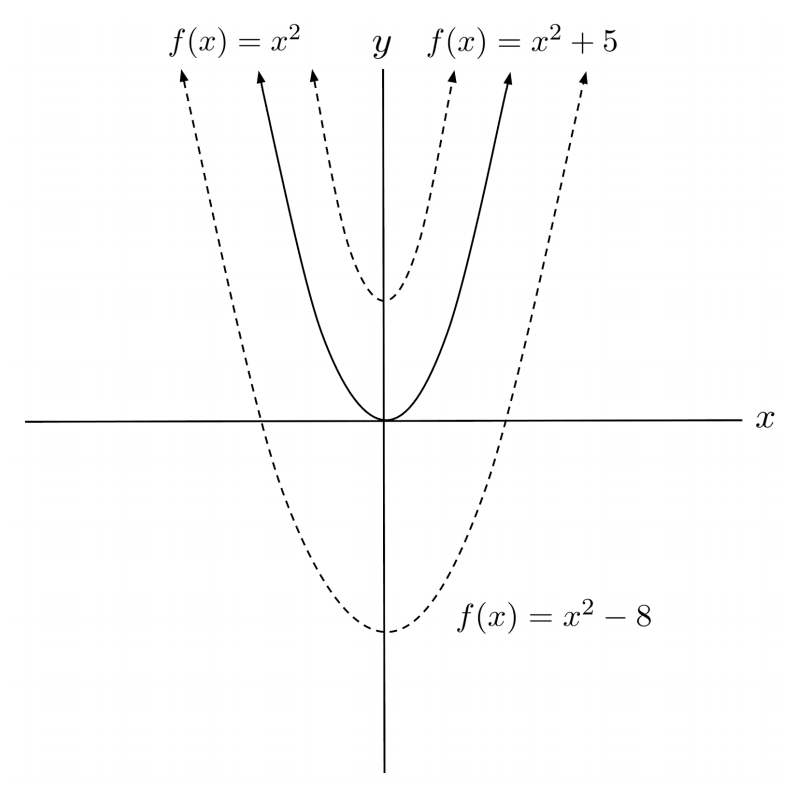
Shifts Inside the Function

On the other hand, when the constant term is added on the inside of a function, e.g. when $f(x)=x^2$ is transformed into $f(x)=(x+4)^2$, the function shifts left by that many units. (If a negative term is added, the function moves right.)

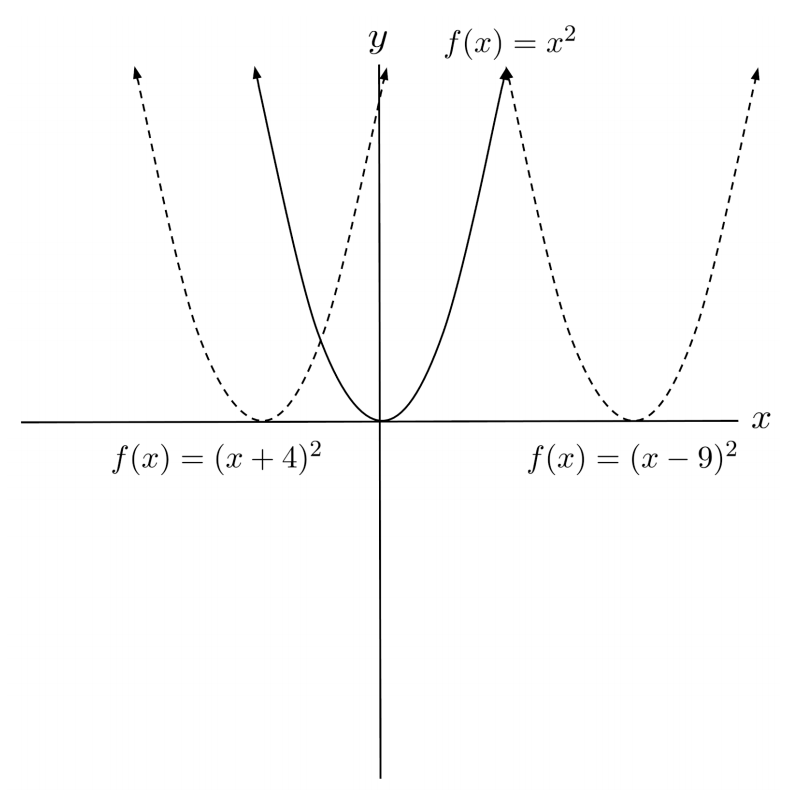
Intuition

Vertical shifts are very intuitive: if we add a number to a function, that number is added to every output of the function. If the number is positive, every output y-value is increased by that amount. If the number is negative, every output y-value is decreased by that amount.

The intuition behind horizontal shifts is a little less straightforward, because ADDING a number inside a function moves it left in the NEGATIVE direction along the x-axis.

But think about it this way: when we transform $f(x)=x^2$ into $f(x)=(x+4)^2$, the output originally at $x=4$ is now at $x=0$, because $4^2$ is the same as $(0+4)^2$. Similarly, the output originally at $x=0$ is now at $x=-4$, because $0^2$ is the same as $(-4+4)^2$. Every input needs to move $4$ units left, to keep its output the same.

Combining Shifts

When we have both vertical and horizontal shifts, it doesn’t matter which we perform first.

For example, to transform $f(x)=\sqrt{x}$ into $f(x)=\sqrt{x+7}+3$, we can either shift it left $7$ units and then up $3$ units, or up $3$ units and then left $7$ units. Either way, we get the same result.

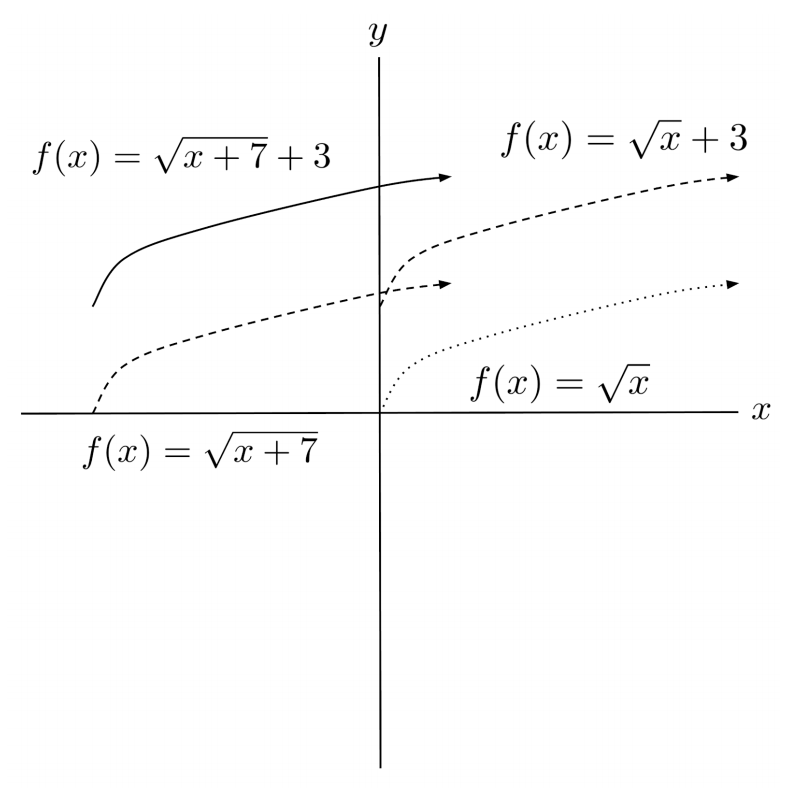
Exercises

Graph the following piecewise functions. (You can view the solution by clicking on the problem.)

$1) \hspace{.5cm} f(x)=x^2+3$

Solution:

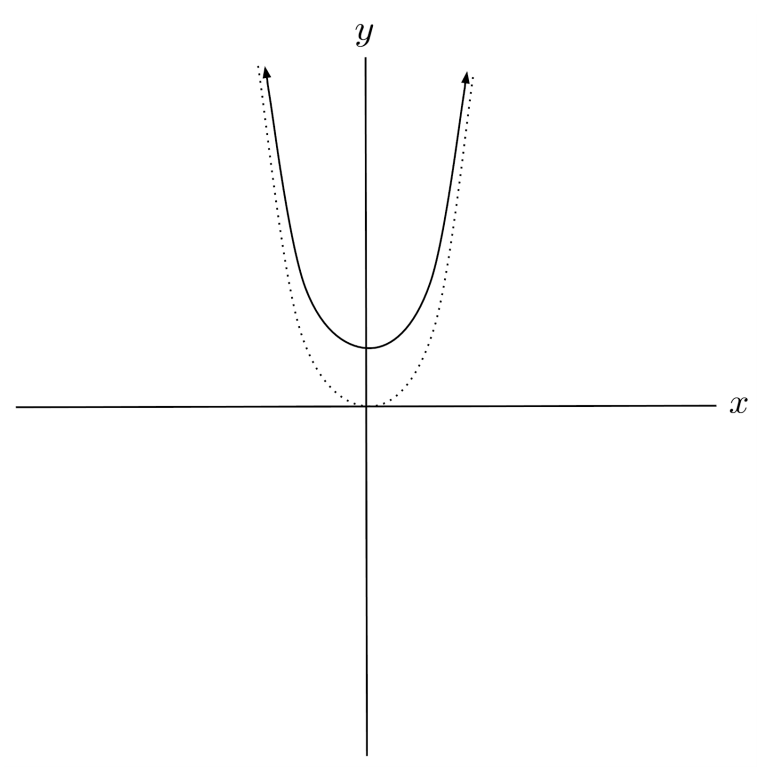
$2) \hspace{.5cm} f(x)=(x+8)^2$

Solution:

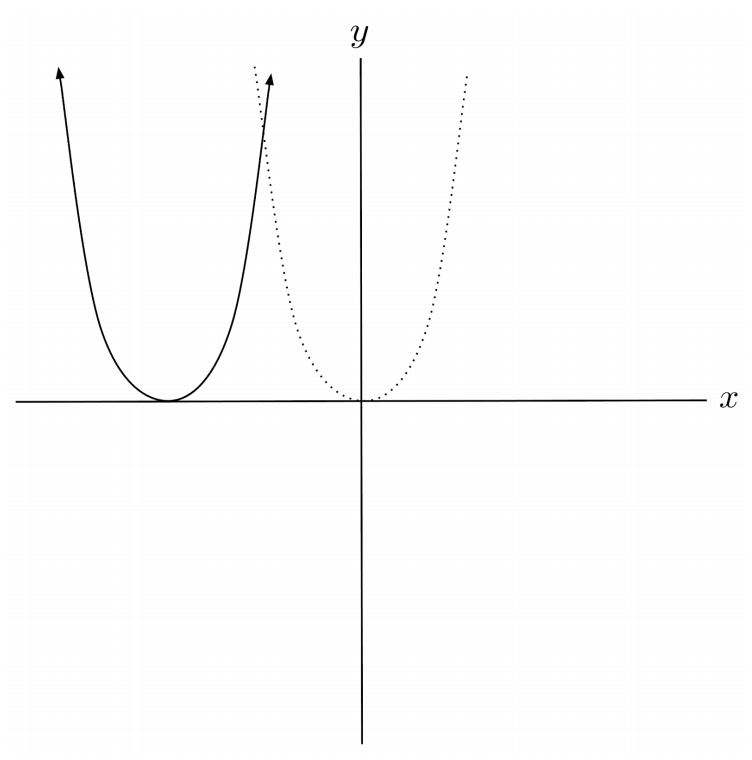
$3) \hspace{.5cm} f(x)=x^3-5$

Solution:

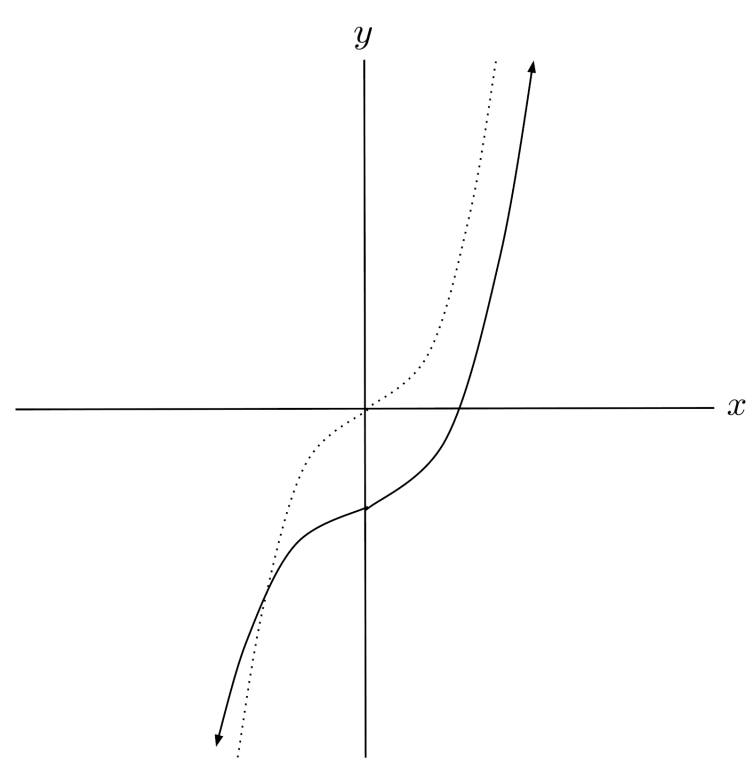
$4) \hspace{.5cm} f(x)=(x-4)^2$

Solution:

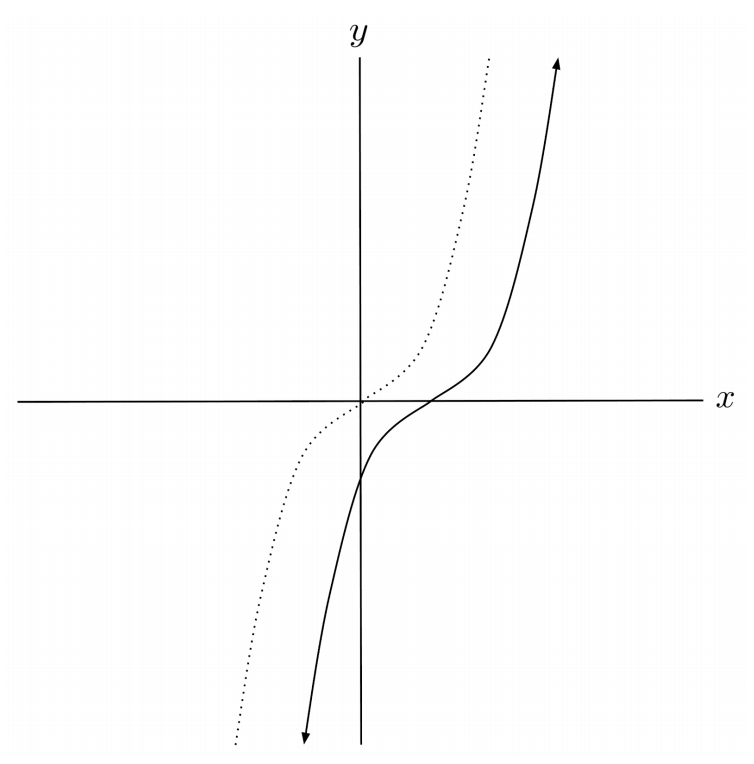
$5) \hspace{.5cm} f(x)=\sqrt{x-3}+7$

Solution:

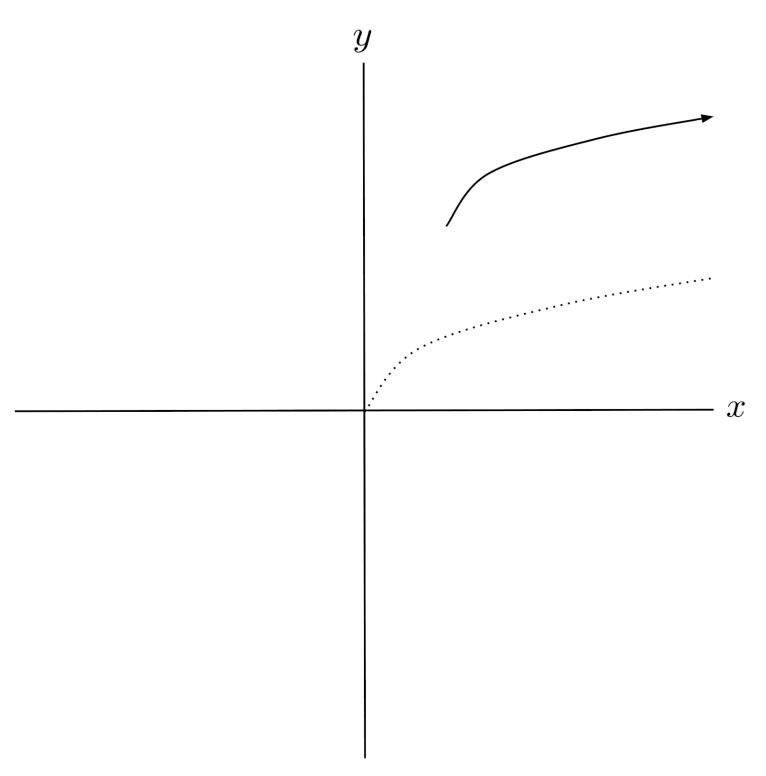
$6) \hspace{.5cm} f(x)=\sqrt[3]{x+4}+6$

Solution:

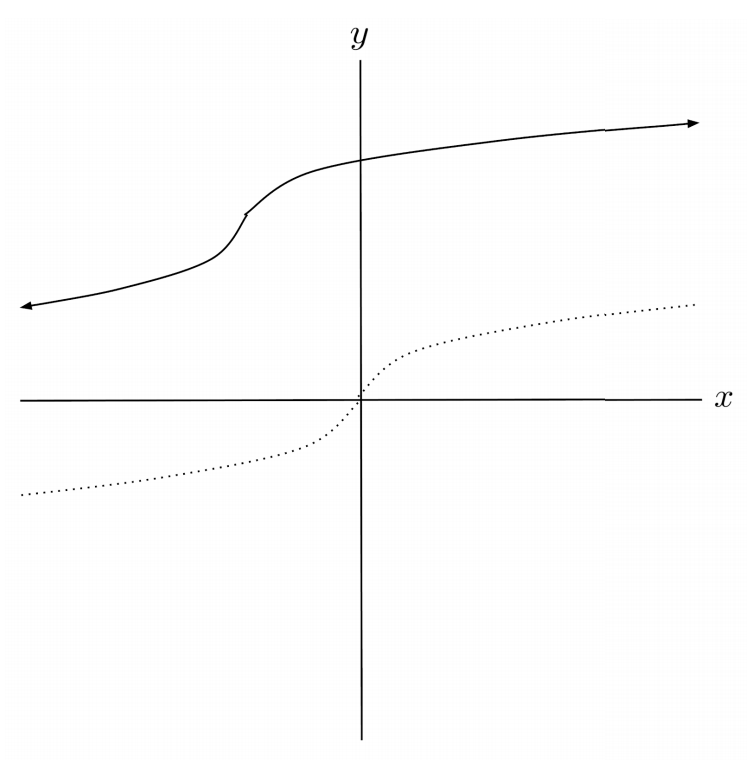
$7) \hspace{.5cm} f(x)=2^{x+2}-4$

Solution:

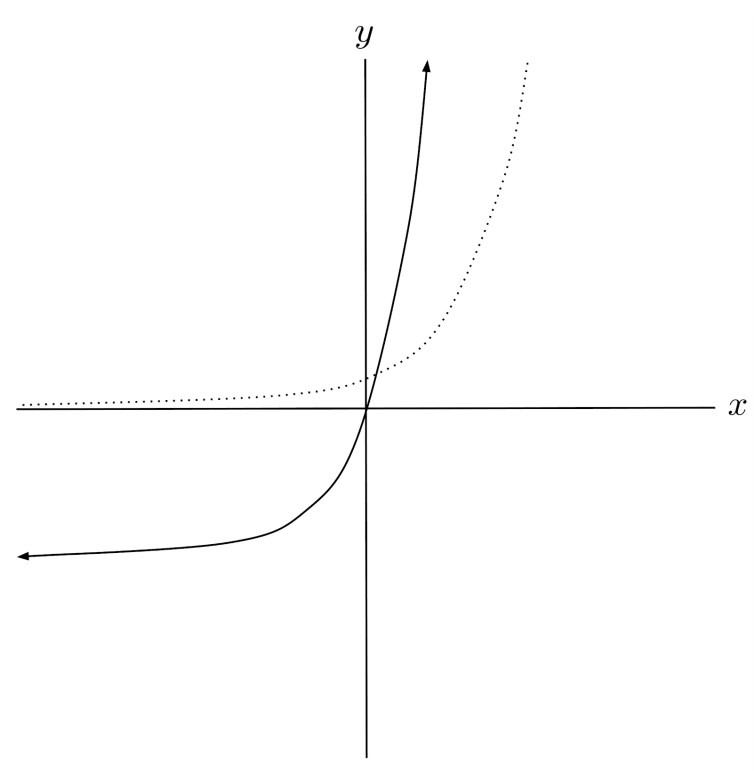
$8) \hspace{.5cm} f(x)=\log_2(x+5)-3$

Solution:

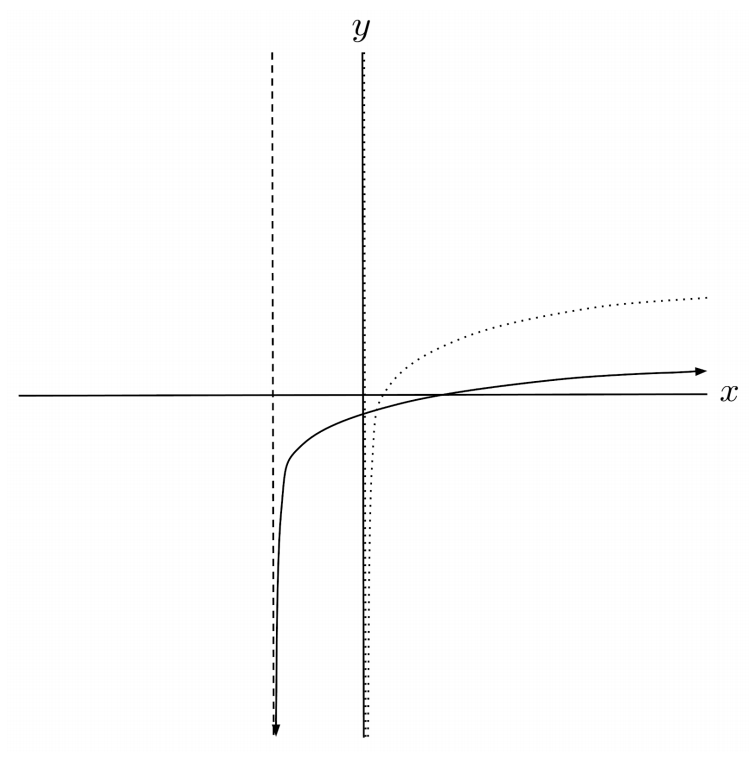
$9) \hspace{.5cm} f(x)=\sin(x-2)-4$

Solution:

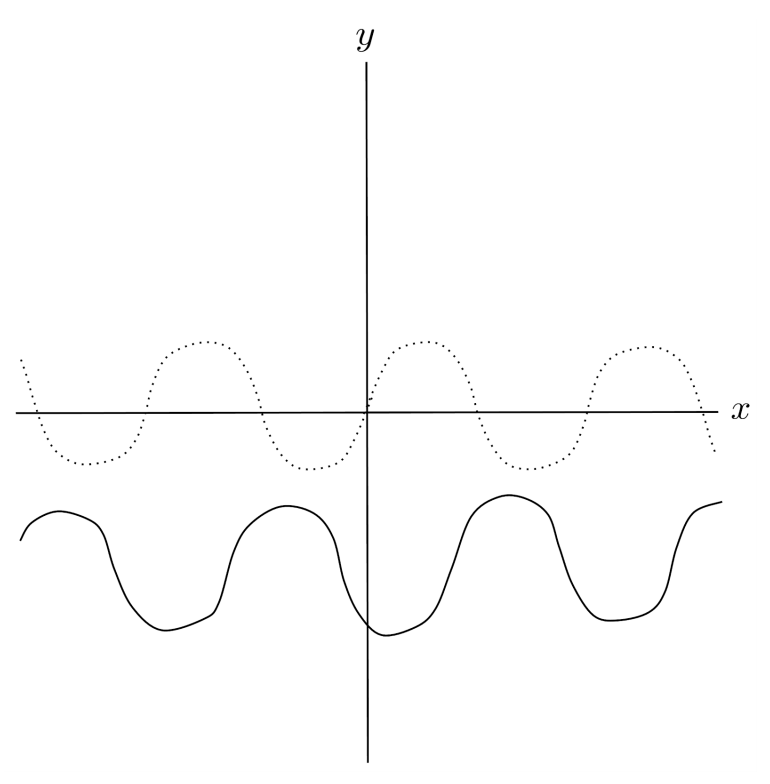
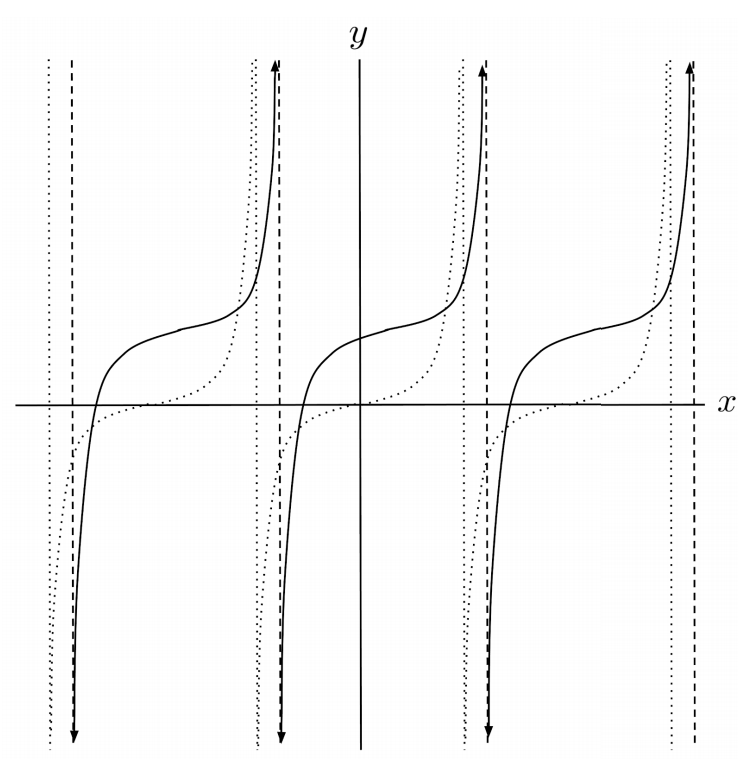
$10) \hspace{.5cm} f(x)=\tan(x-7)+3$

Solution:

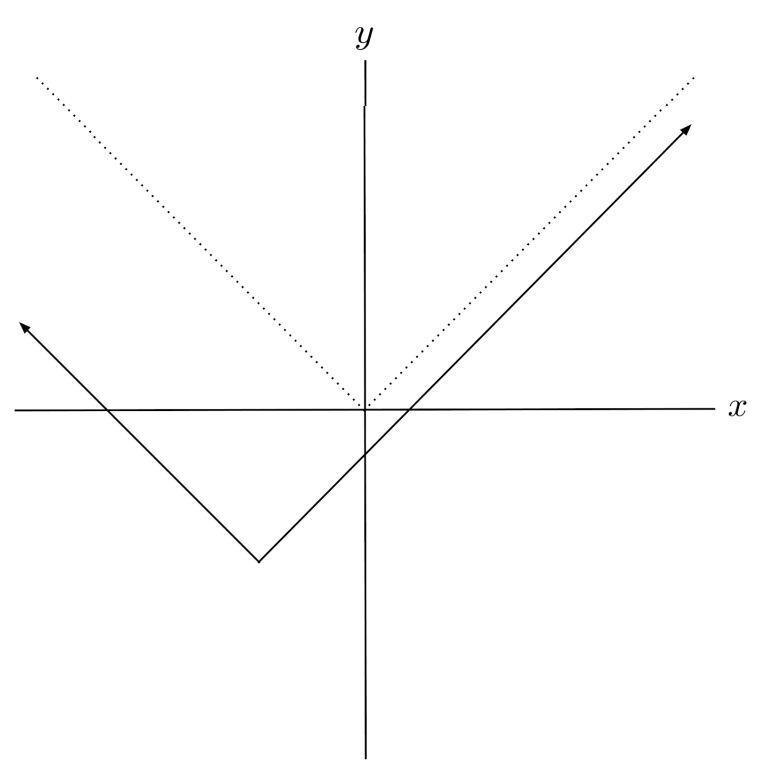
$11) \hspace{.5cm} f(x)=|x+4|-7$

Solution:

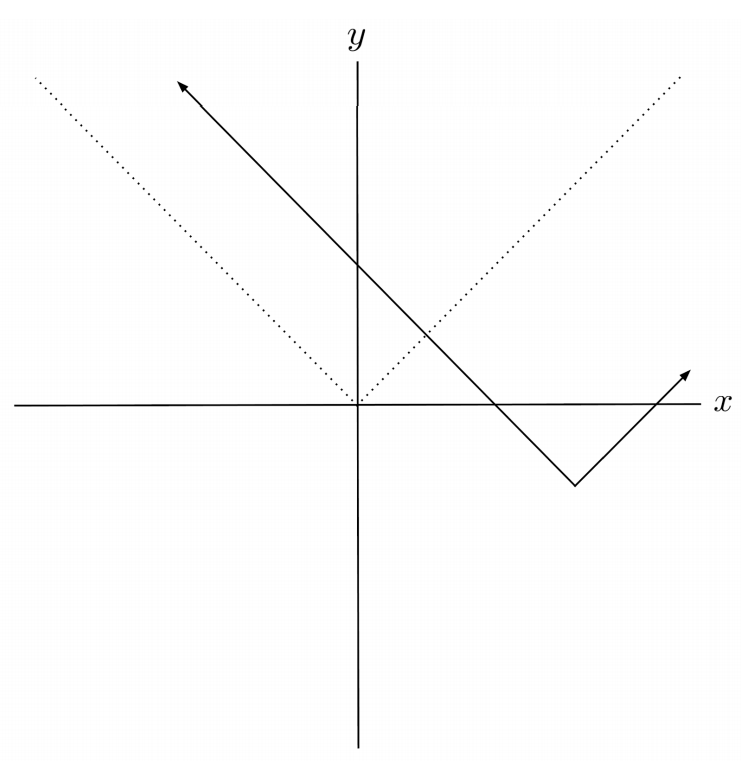
$12) \hspace{.5cm} f(x)=|x-8|-2$

Solution:

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Shifts of Functions. In Justin Math: Algebra. https://justinmath.com/shifts-of-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.