Reflections of Functions

When a function is reflected, it flips across one of the axes to become its mirror image.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Reflections of Functions. In Justin Math: Algebra. https://justinmath.com/reflections-of-functions/

Want to get notified about new posts? Join the mailing list.

When a function is reflected, it flips across one of the axes to become its mirror image.

Reflections occur when a function is made negative – when the negative is outside the function, the reflection is over the y-axis; and when the negative is inside the function, the reflection is over the x-axis.

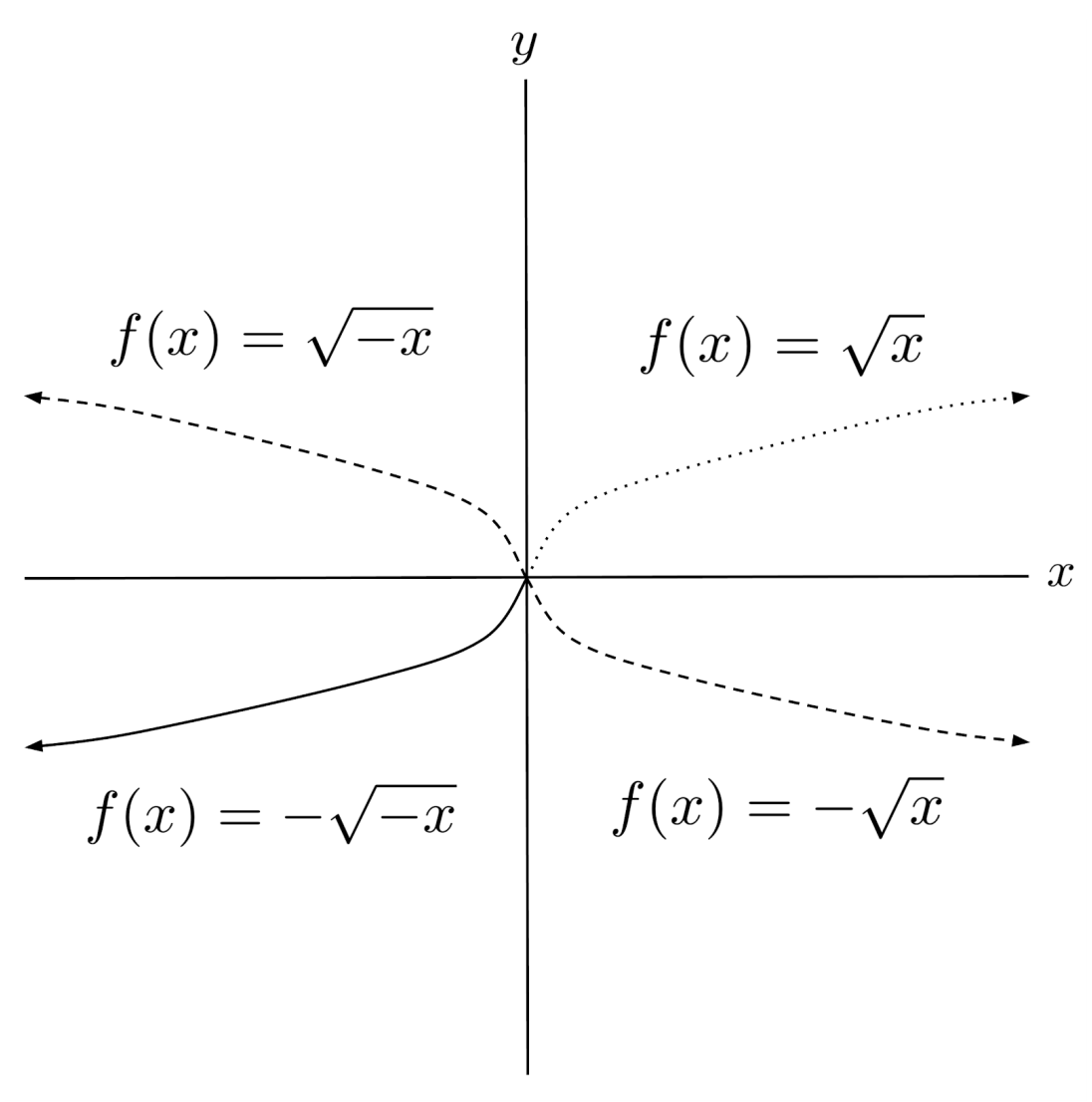
The intuition behind reflections is that, depending where it is placed, the negative sign switches positive and negative values of the $x$ or $y$ variable.

If the negative is outside the function, then the output y-value switches sign, essentially reflecting every point over the x-axis.

On the other hand, if the negative is inside the function, then the input x-value switches sign, essentially reflecting every point over the y-axis.

Order of Function Transformations

When we have both vertical and horizontal reflections, it doesn’t matter which we perform first. Likewise, when dealing with reflections and rescalings simultaneously, it doesn’t matter which we perform first.

However, when dealing with reflections and shifts simultaneously, it’s important to perform horizontal shifts first, then reflections, and lastly vertical shifts.

We are left with an order of function transformations, similar to the concept of order of operations in arithmetic, but different in actual order:

1. Horizontal shifts
2. Rescalings and reflections (interchangeable)
3. Vertical shifts

Exercises

Use reflections and rescalings (followed by shifts) to graph the following functions. (You can view the solution by clicking on the problem.)

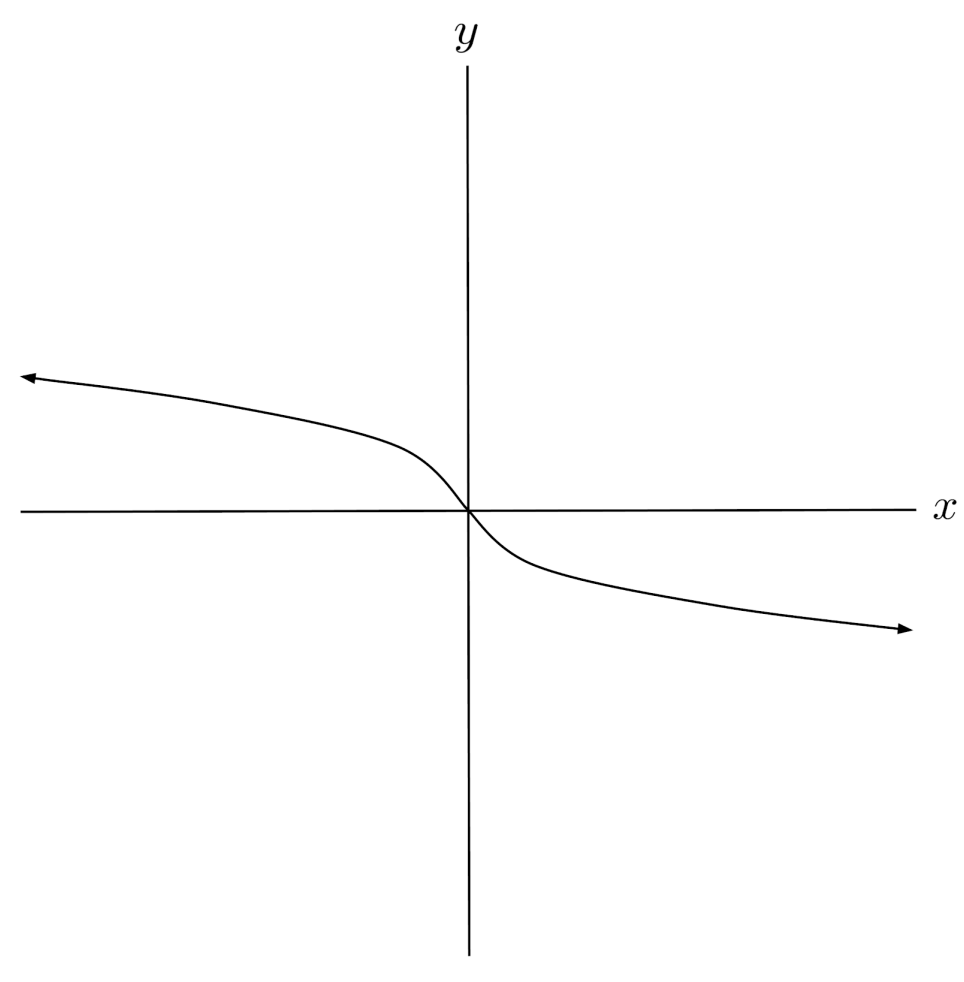
$1) \hspace{.5cm} f(x)= \sqrt[3]{-x}$

Solution:

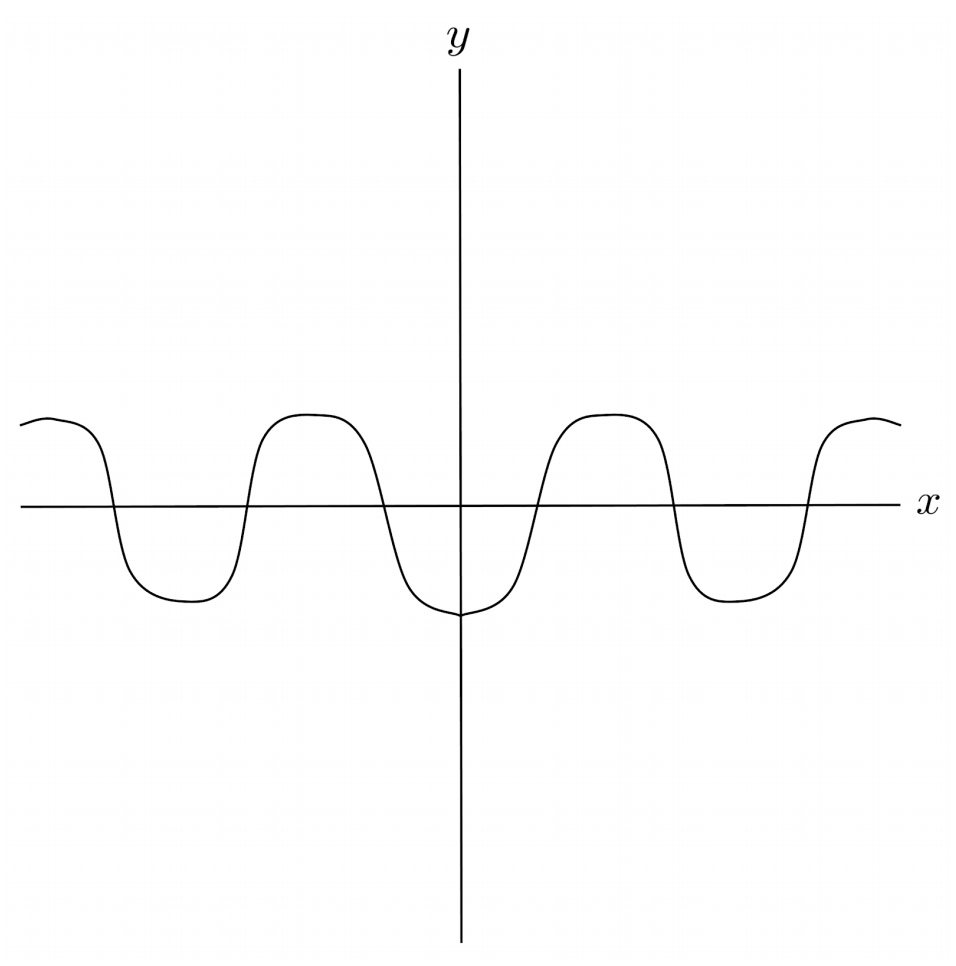
$2) \hspace{.5cm} f(x)= -\cos(-x)$

Solution:

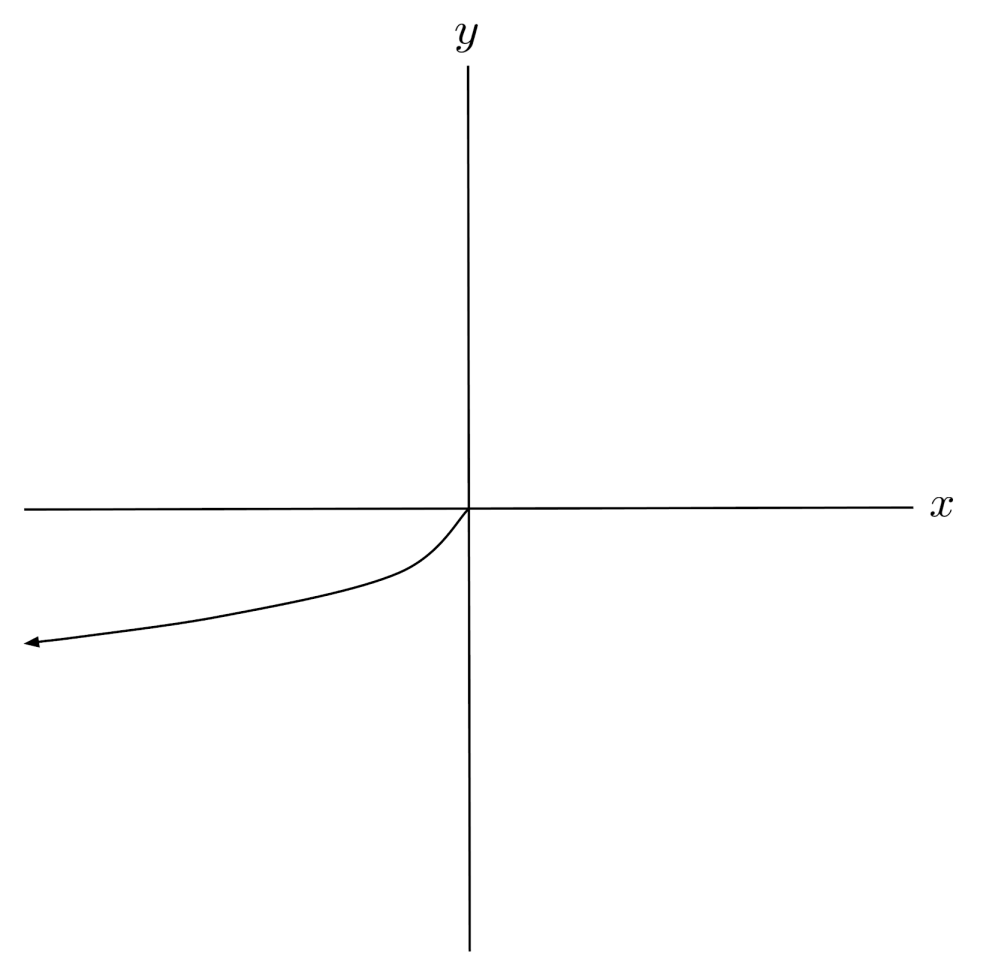
$3) \hspace{.5cm} f(x)= -\sqrt{-x}$

Solution:

$4) \hspace{.5cm} f(x)= -\tan(x)$

Solution:

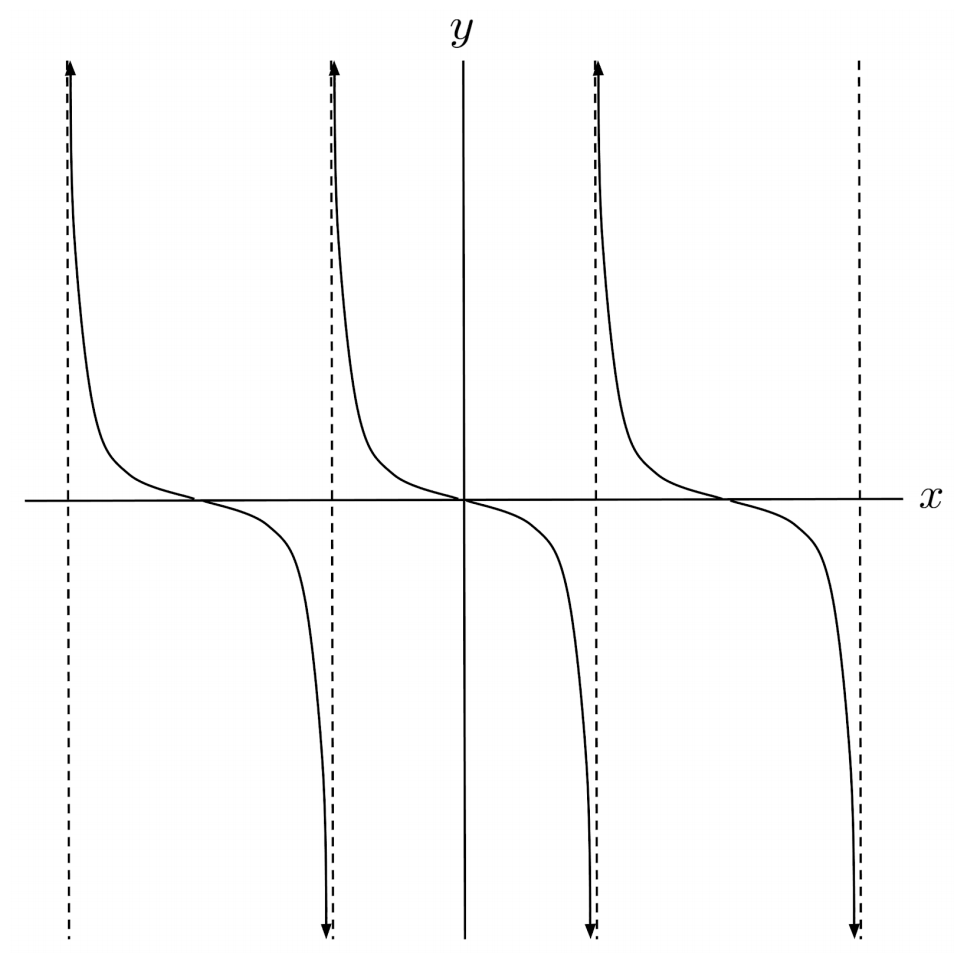
$5) \hspace{.5cm} f(x)= 5 \sqrt{ -\frac{1}{3}x }$

Solution:

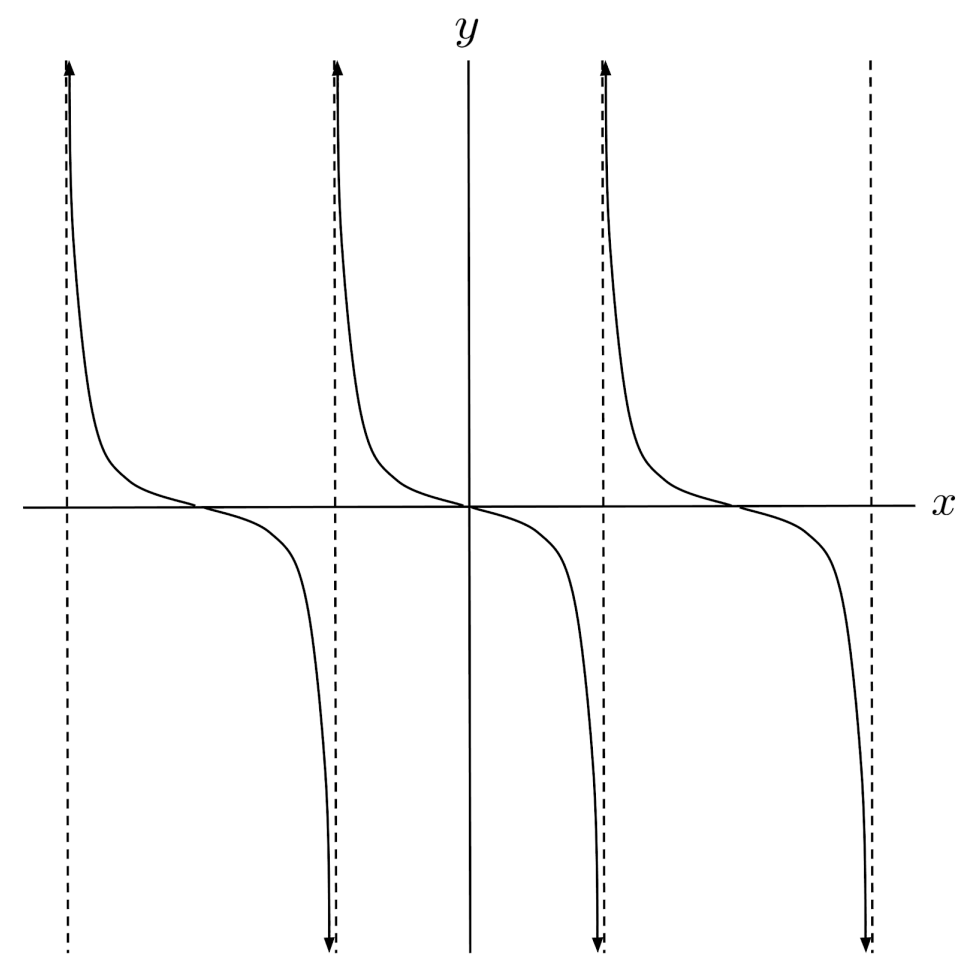
$6) \hspace{.5cm} f(x)= -3 \left( \frac{1}{2} \right)^{-x}$

Solution:

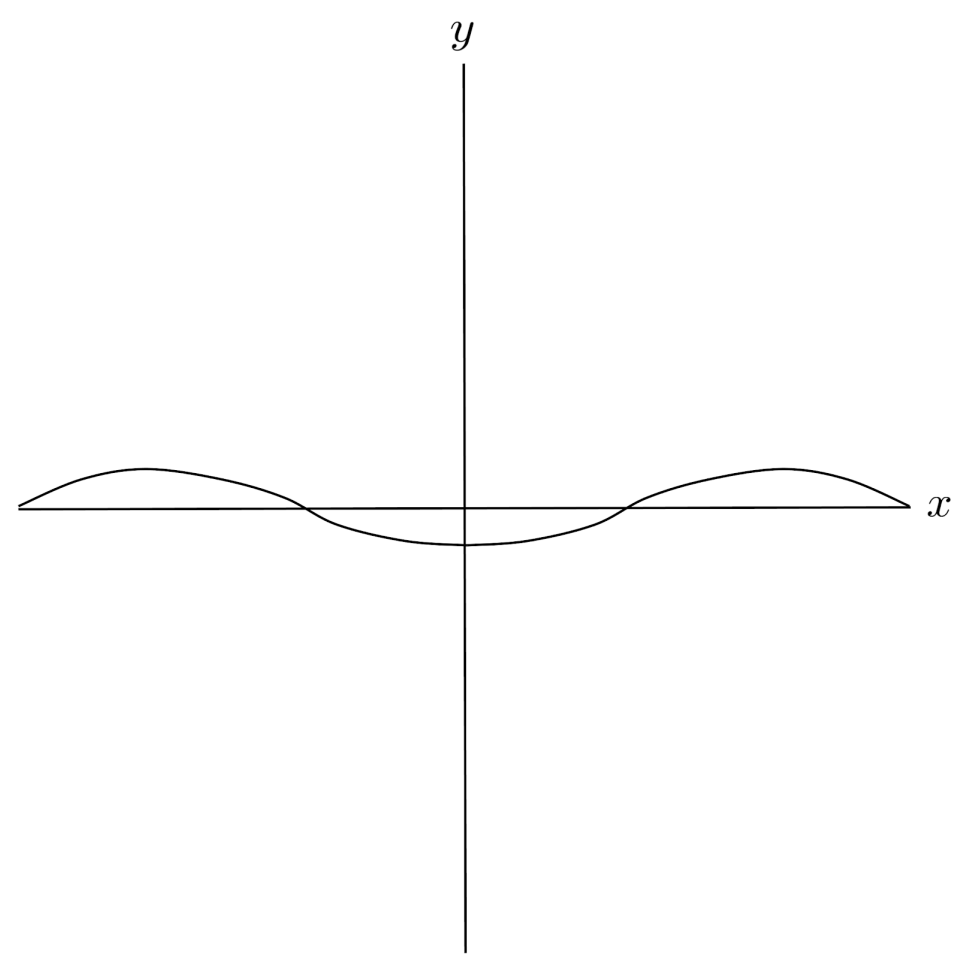
$7) \hspace{.5cm} f(x)= -\frac{1}{2} \cos \left( \frac{1}{4}x \right)$

Solution:

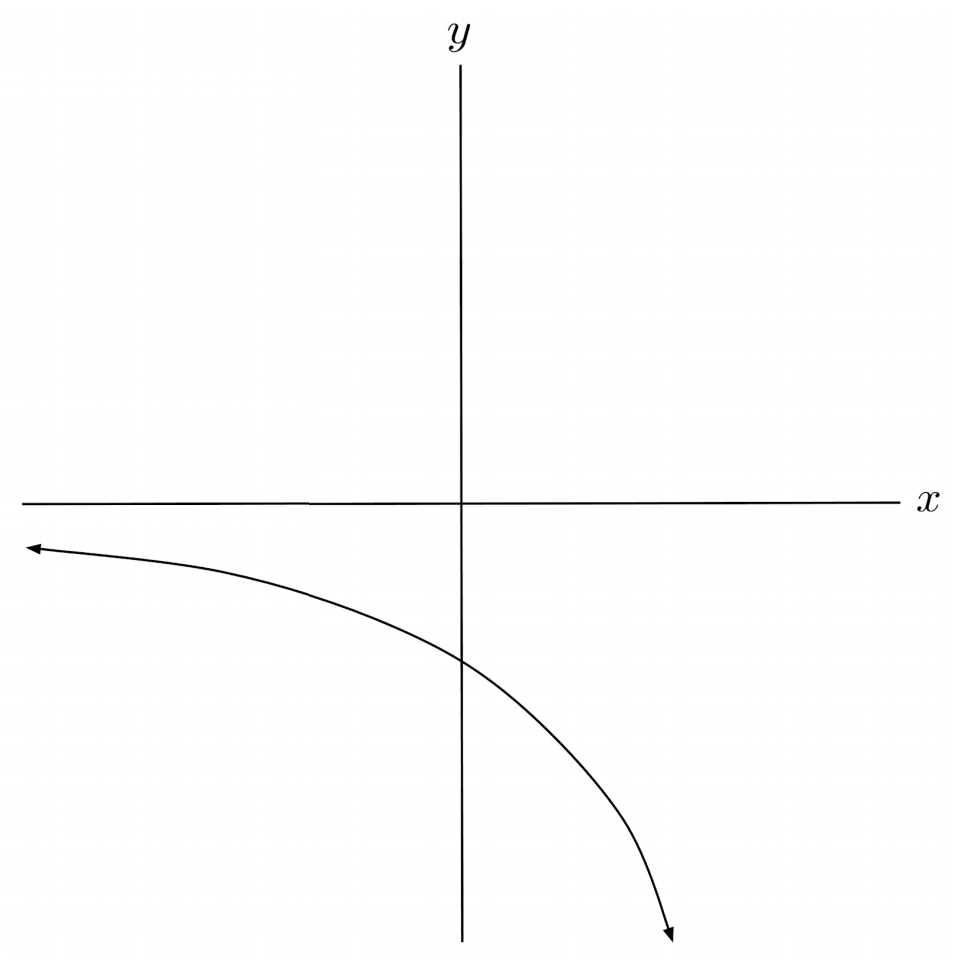
$8) \hspace{.5cm} f(x)= -2 \log_5 \left( -4x \right)$

Solution:

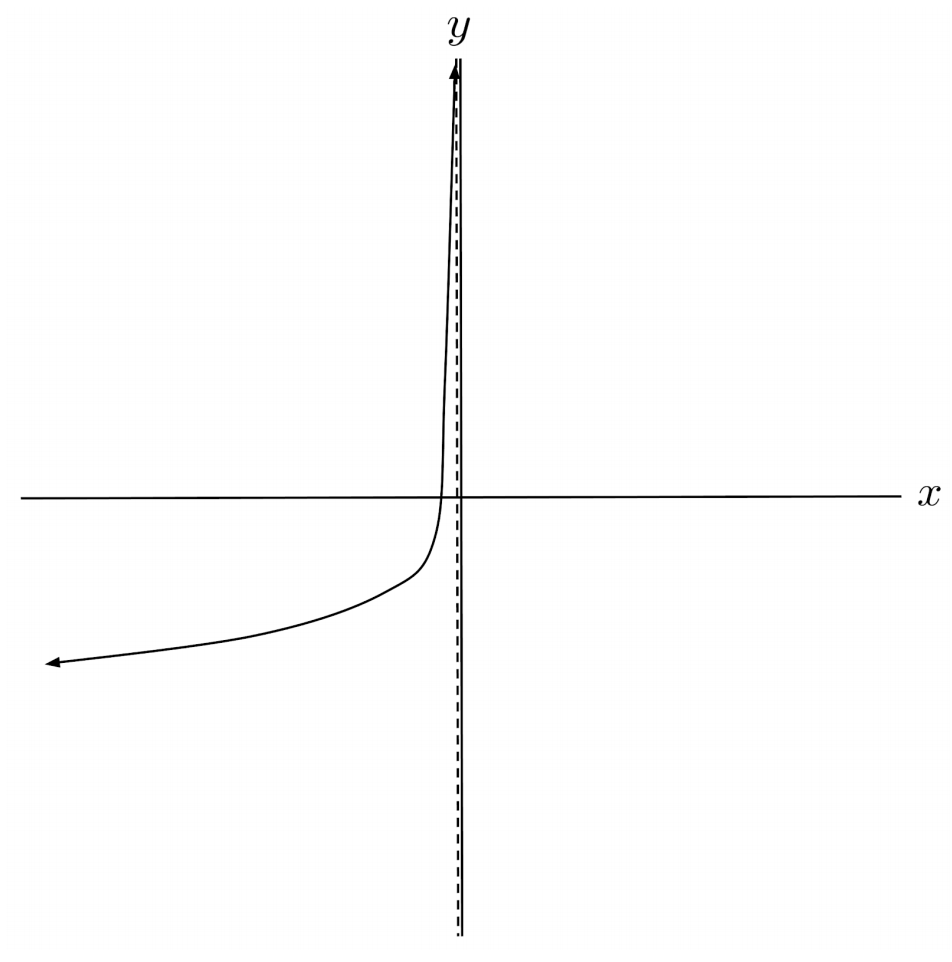
$9) \hspace{.5cm} f(x)= -8 \left| \frac{1}{4}x+2 \right|$

Solution:

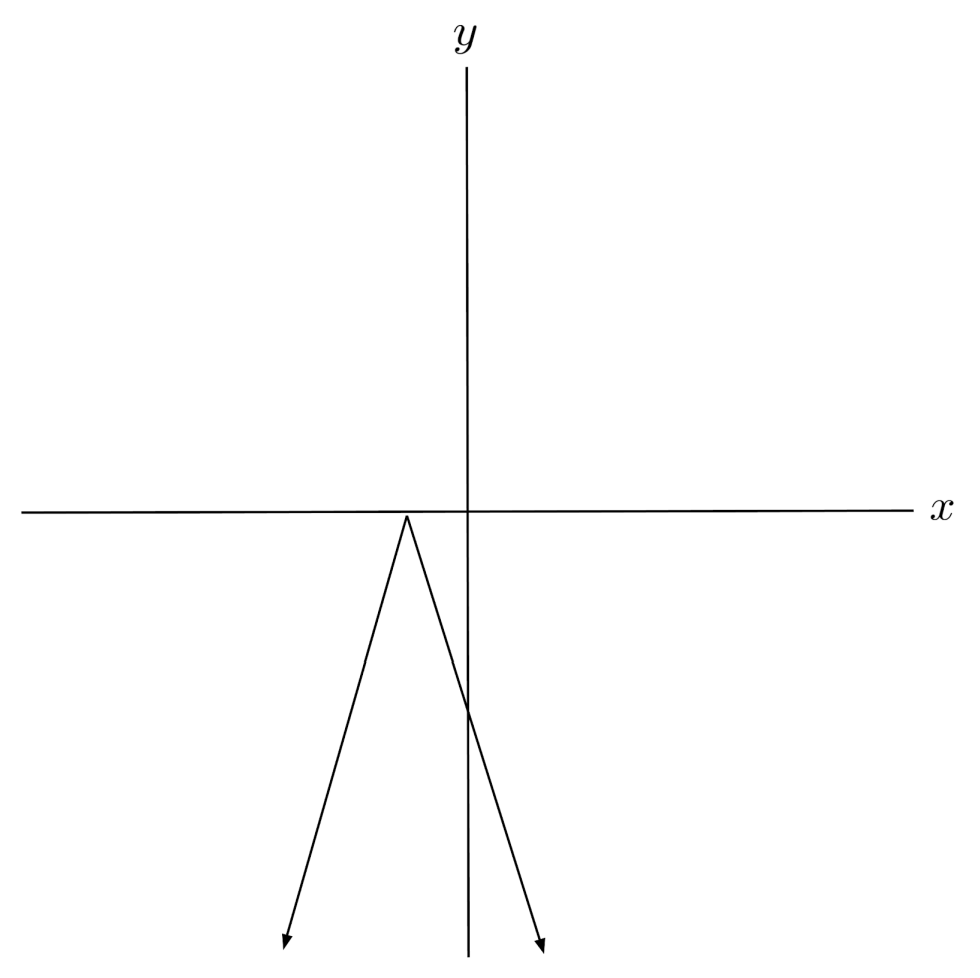
$10) \hspace{.5cm} f(x)= \log_2 (-3x+5)+7$

Solution:

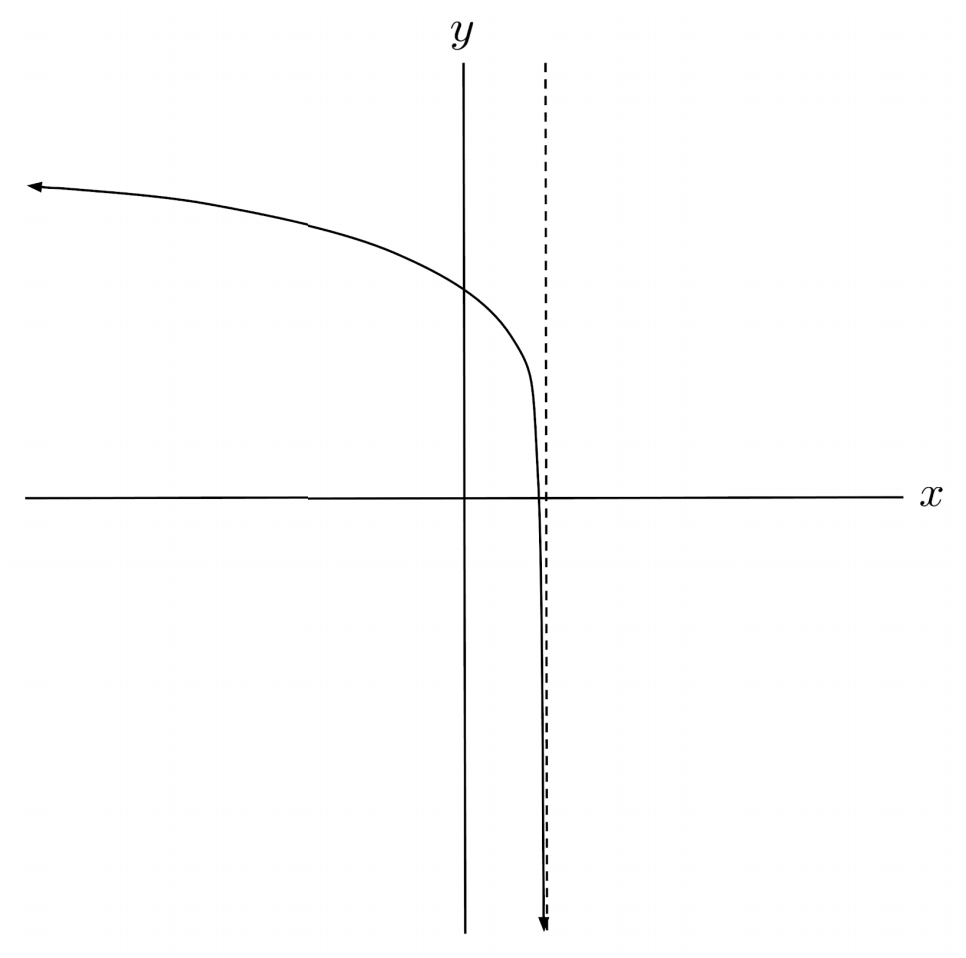
$11) \hspace{.5cm} f(x)= -\tan \left( \frac{1}{3}x-3 \right)-5$

Solution:

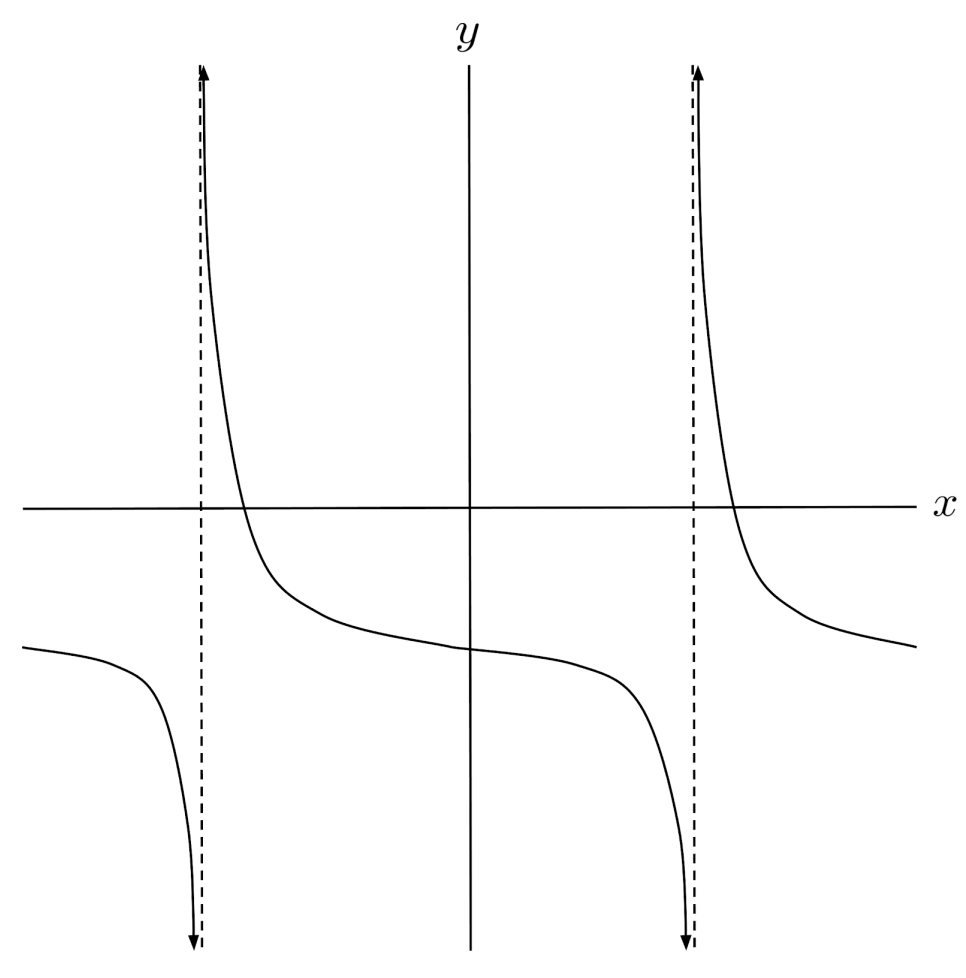
$12) \hspace{.5cm} f(x)= -2 \sqrt{ -\frac{1}{2}x+2 }+4$

Solution:

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Reflections of Functions. In Justin Math: Algebra. https://justinmath.com/reflections-of-functions/

Want to get notified about new posts? Join the mailing list.