Quadratic Formula

by Justin Skycak (@justinskycak) on February 12, 2018

To solve hard-to-factor quadratic equations, it's easiest to use the quadratic formula.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Quadratic Formula. In Justin Math: Algebra. https://justinmath.com/quadratic-formula/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Some quadratic equations cannot be factored easily. For example, in the equation $x^2+3x+1=0$, we need to find two factors of $1$ that add to $3$. But the only integer factors of $1$ are $1$ and $1$, and they definitely don’t add to $3$!

To solve these hard-to-factor quadratic equations, it’s easiest to use the quadratic formula given below, which tells us explicitly how to compute the solutions of a quadratic equation $ax^2+bx+c=0$.

$x= \dfrac{-b \pm \sqrt{b^2-4ac} }{2a}$

Worked Example

Using the quadratic formula, we can compute the solutions to the equation $x^2+3x+1=0$.

$\begin{align*} \begin{matrix} \text{Substitute} a=1 \text{, }b=3\text{, and} \\ c=1 \text{ in quadratic formula} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} x = \frac{-3 \pm \sqrt{ (3)^2 - 4(1)(1)} }{2(1)} \\ \text{Simplify} \hspace{.5cm} &\Bigg| \hspace{.5cm} x = \frac{-3 \pm \sqrt{5} }{2} \\ \begin{matrix} \text{Separate the } \pm \text{ into two} \\ \text{solutions (optional)} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} x = \frac{-3 + \sqrt{5} }{2} \text{ or } x = \frac{-3 - \sqrt{5} }{2} \end{align*}$

These solutions look weird, but they’re correct.

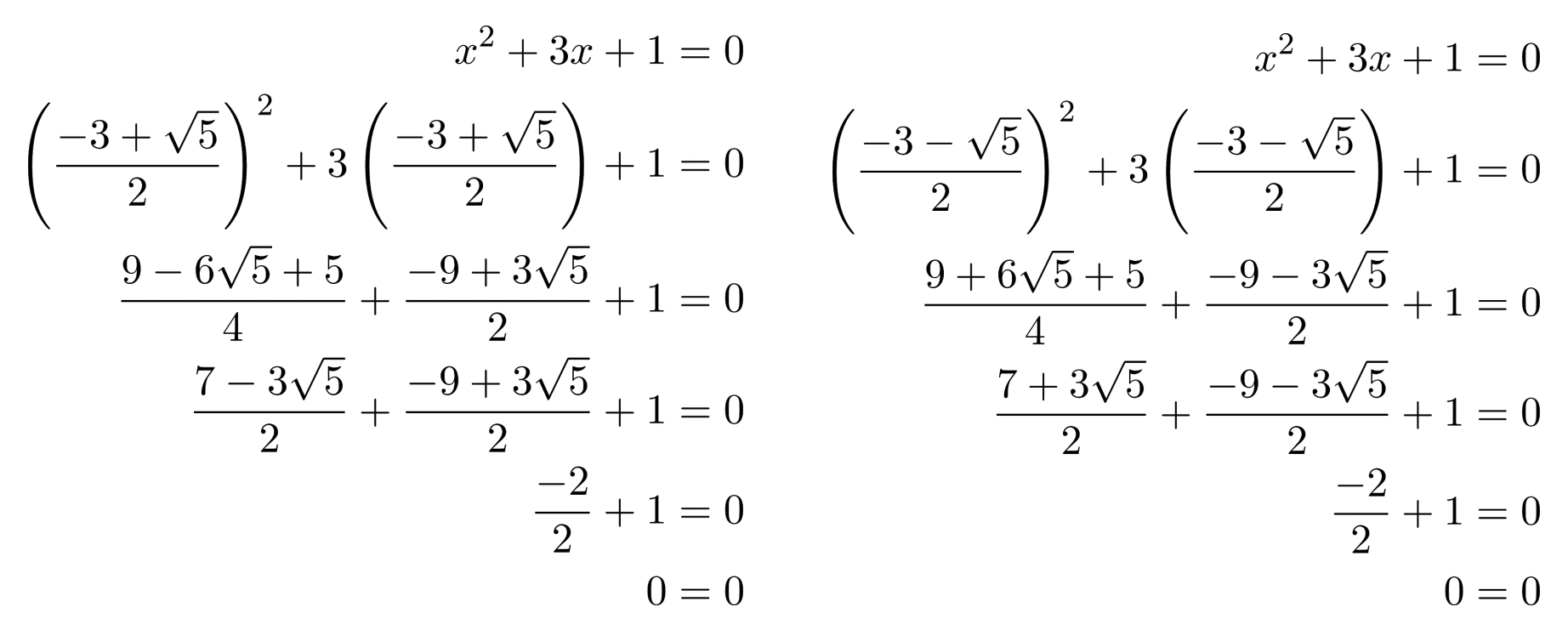
Reverse Derivation

To gain some faith in the quadratic formula, we can also rearrange it back into the original equation to see that it must have the same solutions as the original equation:

$\begin{align*} x &= \frac{-b \pm \sqrt{b^2-4ac} }{2a} \\ 2ax &= -b \pm \sqrt{ b^2 - 4ac} \\ 2ax+b &= \pm \sqrt{ b^2 - 4ac} \\ (2ax+b)^2 &= \left( \pm \sqrt{ b^2 - 4ac} \right)^2 \\ 4a^2x^2 + 4abx + b^2 &= b^2 - 4ac \\ 4a^2x^2 + 4abx + 4ac &= 0 \\ 4a(ax^2 + bx + c ) &= 0 \\ ax^2 + bx + c &= 0 \end{align*}$

The Discriminant

Using the quadratic equation, we can see that some quadratic equations have 2 solutions (as usual), but other quadratic equations can have just 1 solution, or no solutions at all.

For example, using the quadratic equation to solve $x^2+2x+1$, we find a single solution because the $\pm \sqrt{b^2 - 4ac}$ part comes out to $\pm 0$.

$x = \dfrac{-2 \pm \sqrt{2^2 - 4(1)(1)}}{2(1)} = \dfrac{-2 \pm 0}{2} = -1$

Similarly, using the quadratic equation to solve $x^2+2x+2$, we find no solutions because the $\pm \sqrt{b^2-4ac}$ part comes out to $\pm \sqrt{ \text{negative number} }$, and we can’t take the square root of a negative number. (We’ll ignore imaginary solutions and consider only real solutions for now.)

$x = \dfrac{-2 \pm \sqrt{2^2 - 4(1)(2)}}{2(1)} = \dfrac{-2 \pm \sqrt{-4} }{2} = \text{no solution}$

To see how many solutions a quadratic equation has, we need only consider the $b^2-4ac$ part of the quadratic formula, which is called the discriminant. If the discriminant is positive, then we have two solutions. If it is $0$, then we have one solution. If it is negative, then we have no solution.

We can also use the quadratic formula to understand the trick for factoring when $a$ is not equal to $1$ – which was to multiply $c$ by $a$, replace $a$ with $1$, factor the result, divide each constant in each factor by the original $a$, and move denominators onto our variables.

From the quadratic formula, we know that the solutions of $ax^2+bx+c=0$ are given by $x = \frac{-b \pm \sqrt{b^2-4ac} }{2a}$. When we multiply $c$ by $a$ and replace $a$ with $1$, we have the equation $x^2+bx+ac=0$, which has solutions $x= \frac{-b \pm \sqrt{b^2-4ac}}{2}$.

This means that if $x$ is a solution of $x^2+bx+ac=0$, then $ax$ is a solution of $ax^2+bx+c$.

Thus, if $x^2+bx+ac$ factors into $(x+m)(x+n)$, then $ax^2+bx+c$ factors into $a \left( x+\frac{m}{a} \right) \left( x+\frac{n}{a} \right)$.

Exercises

Use the quadratic formula to solve the following quadratic equations. (You can view the solution by clicking on the problem.)

$1) \hspace{.5cm} x^2+3x-7=0$

Solution:
$x = \frac{-3 \pm \sqrt{37}}{2}$

$2) \hspace{.5cm} 4x^2-12x+9=0$

Solution:
$x = \frac{3}{2}$

$3) \hspace{.5cm} -2x^2+4x+6=0$

Solution:
$x = -1 \text{ or } x=3$

$4) \hspace{.5cm} 3x^2-x+5=0$

Solution:
$\text{no solution}$

$5) \hspace{.5cm} -25x^2-20x=4$

Solution:
$x = -\frac{2}{5}$

$6) \hspace{.5cm} 3x^2=2x+3$

Solution:
$x = \frac{1 \pm \sqrt{10}}{3}$

$7) \hspace{.5cm} 42x=9x^2+49$

Solution:
$x = \frac{7}{3}$

$8) \hspace{.5cm} 8x^2+5=3x$

Solution:
$\text{no solution}$

$9) \hspace{.5cm} 1+3x=5x^2$

Solution:
$x = \frac{3 \pm \sqrt{29}}{10}$

$10) \hspace{.5cm} 154x=121x^2+49$

Solution:
$x = \frac{7}{11}$

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Quadratic Formula. In Justin Math: Algebra. https://justinmath.com/quadratic-formula/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.