Point-Slope Form

An easy way to write the equation of a line if we know the slope and a point on a line.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Point-Slope Form. In Justin Math: Algebra. https://justinmath.com/point-slope-form/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Suppose we want to write the equation of a line with a given slope $m=2$, through a particular point $(3,5)$. In the previous post, we substituted the given information into a slope-intercept equation form $y=mx+b$, solved for $b$, and rewrote the slope-intercept form with $m$ and $b$ substituted so that $x$ and $y$ were the only variables.

However, there is an alternative form, point-slope form, that makes it even easier to write the equation of a line if we know the slope and a point $(x_0,y_0)$ on the line. It is given by

If we know that our desired line has slope $m=2$ and passes through the point $(x_0,y_0)=(3,5)$, then we can substitute directly into point-slope form without performing any additional computations:

This is an accepted form of the equation for a line, so we don’t need to simplify it at all unless we’re asked to do so.

But even if we actually need to find the line in slope-intercept form, it’s still advantageous to begin with point-slope form, because all we have to do is distribute the $2$ and add $5$ to get to slope-intercept form.

Derivation

The point-slope formula is easy to remember, too, because it just says that the slope between any point $(x,y)$ and the reference point $(x_0,y_0)$ needs to be equal to the given slope $m$.

Moving from $(x_0,y_0)$ to $(x,y)$, the amount we go up is $y-y_0$, and the amount we go over horizontally is $x-x_0$, so the slope is just $\frac{y-y_0}{x-x_0}$. Equating this to $m$ and multiplying to get rid of the fraction, we reach point-slope form!

Graphing

To graph a line whose equation is given in point-slope form, we perform the same process as we do to graph a line that is in slope-intercept form, except we start at the reference point rather than at the y-intercept.

For example, consider the line $y-4 = \frac{3}{2}(x-1)$, for which the reference point is $(1,4)$ and the slope is $\frac{3}{2}$. To graph this line, we start at $(1,4)$, go up $3$ and over $2$ to the point $(3,7)$, and draw a line through the two points.

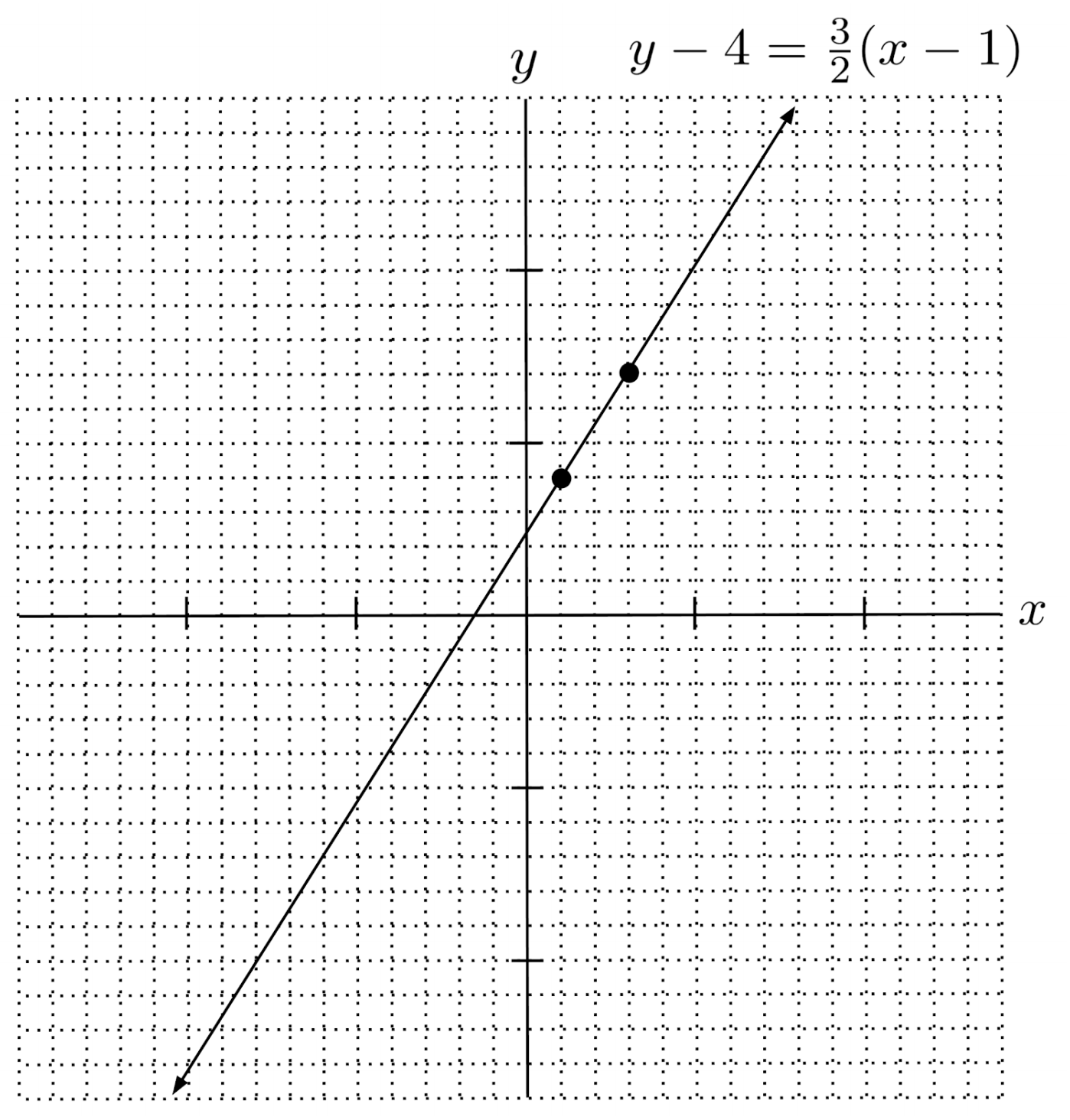
Final Remark

One thing to watch out for in point-slope form: be careful about negatives.

For example, the point-slope form of a line with slope $2$ that goes through the point $(-3,-5)$ is NOT given by $y-5=2(x-3)$. This is the line that goes through the point $(3,5)$, not $(-3,-5)$.

The line that goes through $(-3,-5)$ actually involves addition rather than subtraction, because the negatives cancel the subtraction in the original formula for point-slope form.

Exercises

Write the point-slope equation of the line that goes through the given point, with the given slope. (You can view the solution by clicking on the problem.)

Write the point-slope equation of the line that goes through the given points. (You can view the solution by clicking on the problem.)

Graph the following lines. (You can view the solution by clicking on the problem.)

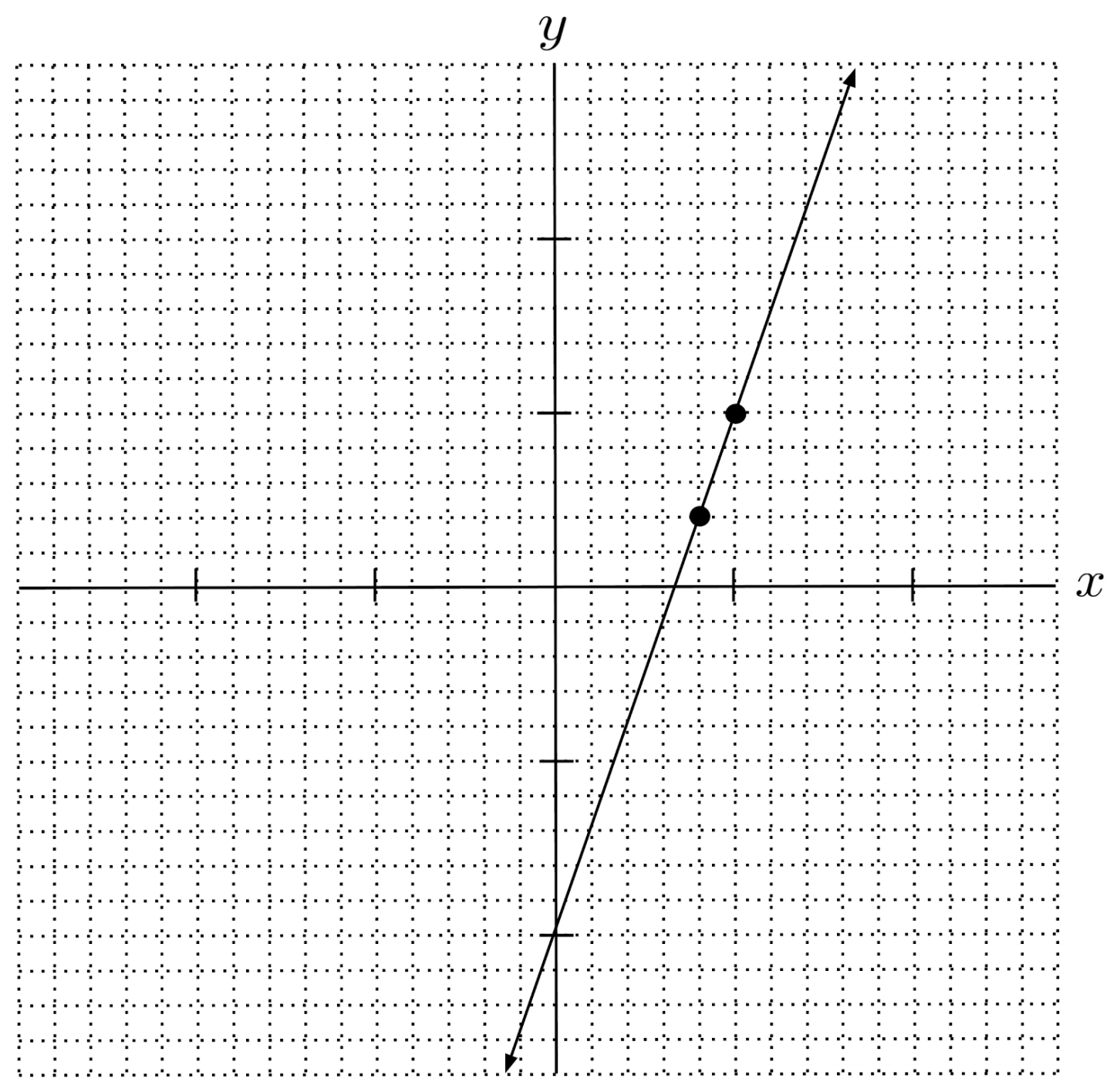
$9) \hspace{.5cm} y-2=3(x-4)$

Solution:

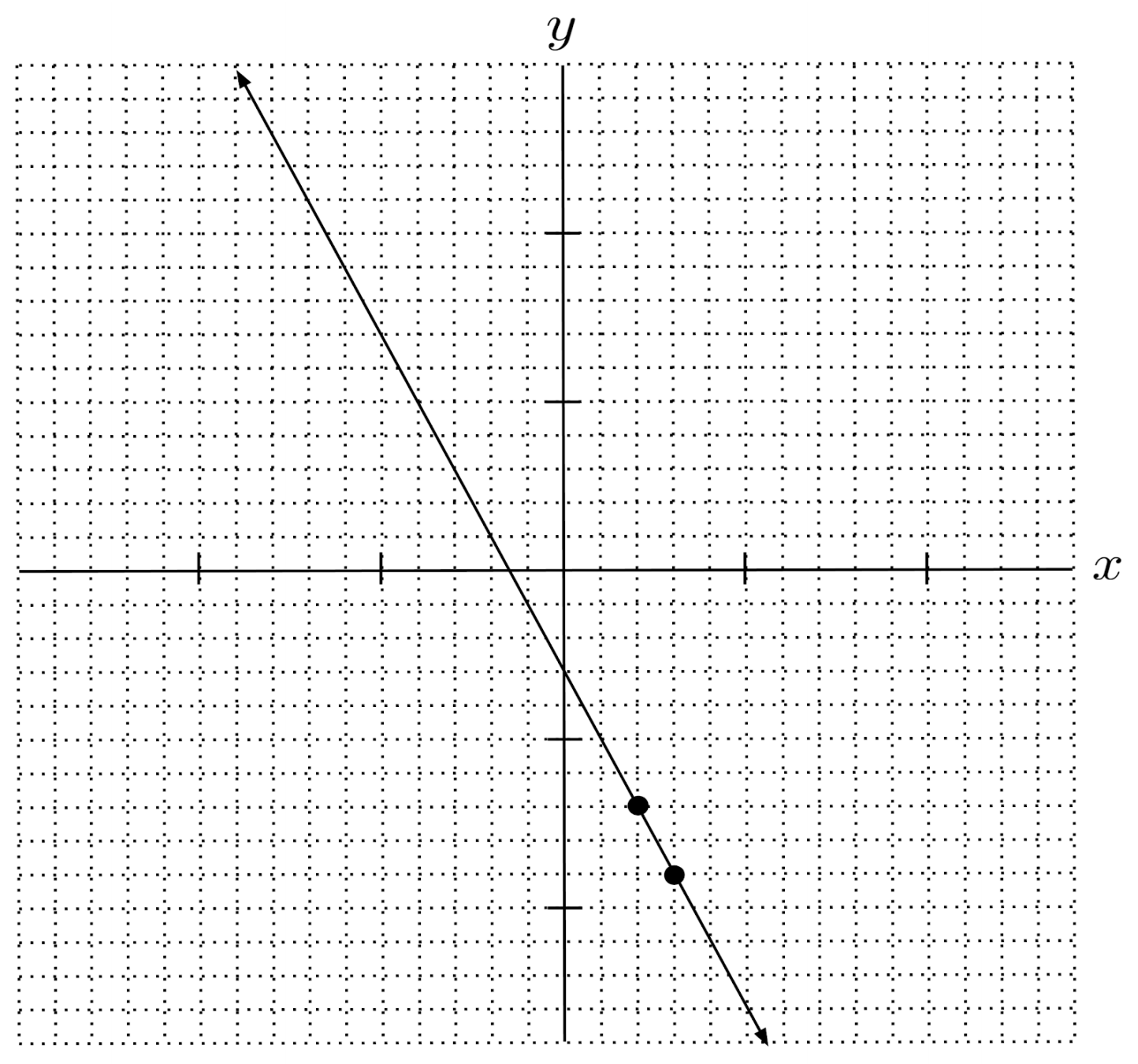
$10) \hspace{.5cm} y+7=-2(x-2)$

Solution:

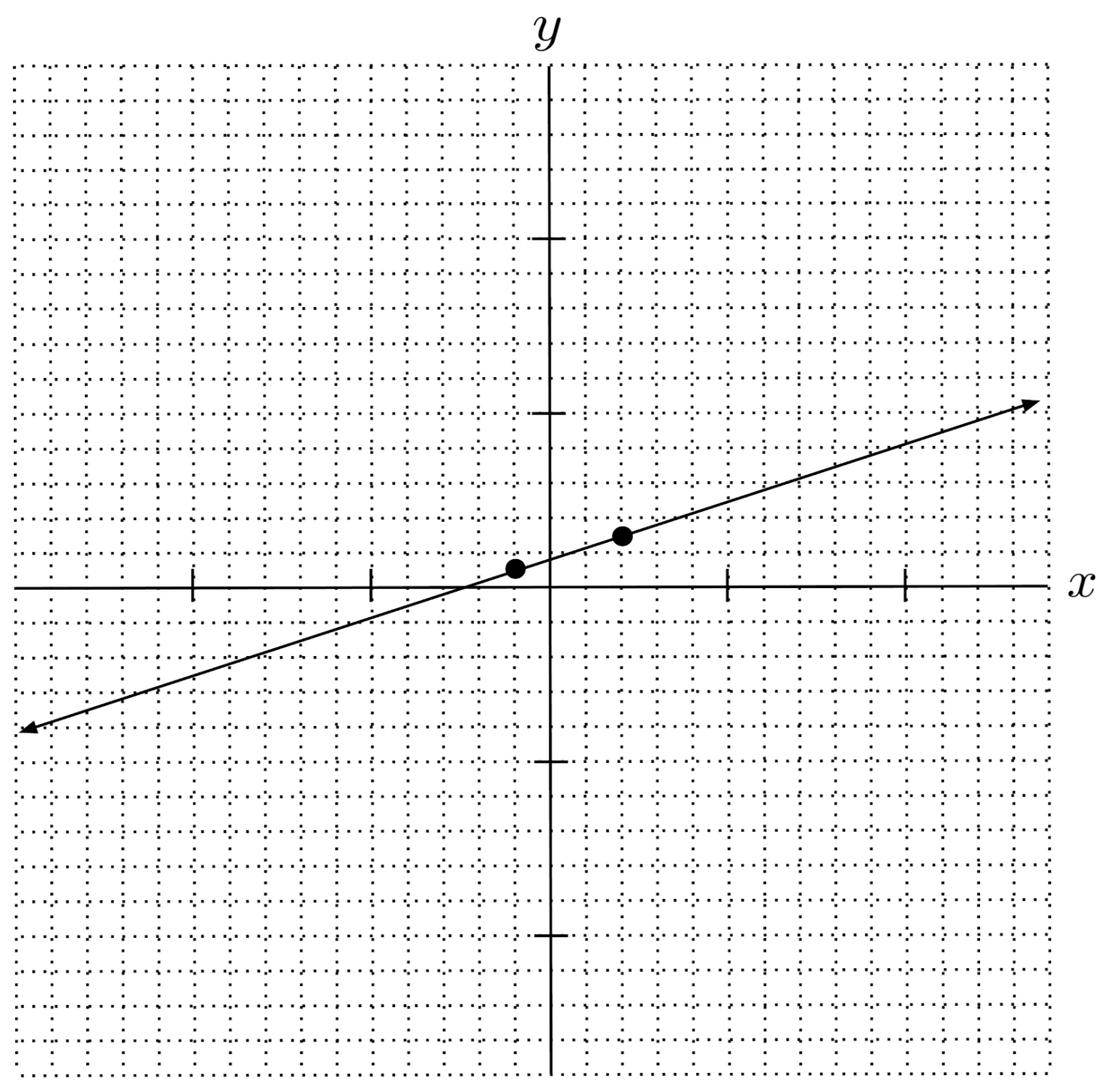
$11) \hspace{.5cm} y-\frac{1}{2} = \frac{1}{3}(x+1)$

Solution:

$12) \hspace{.5cm} y+\frac{5}{2} = -\frac{2}{5}\left( x-\frac{1}{4} \right)$

Solution:

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Point-Slope Form. In Justin Math: Algebra. https://justinmath.com/point-slope-form/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.