Piecewise Functions

by Justin Skycak (@justinskycak) on June 05, 2018

A piecewise function is pieced together from multiple different functions.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Piecewise Functions. In Justin Math: Algebra. https://justinmath.com/piecewise-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

A piecewise function is pieced together from multiple different functions.

For example, the absolute value function is a piecewise function because it consists of the line $y=-x$ for negative $x$, and $y=x$ for positive $x$.

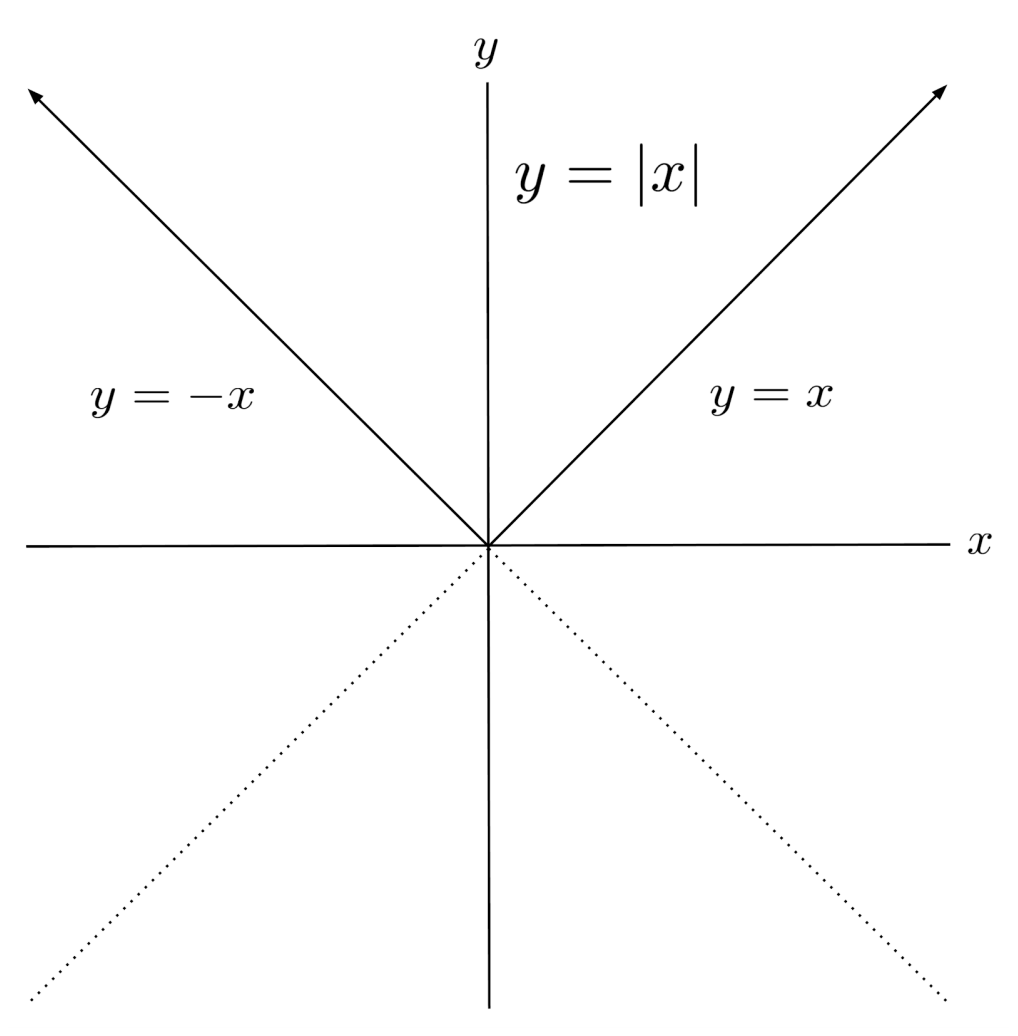
Case Notation

More generally, piecewise functions can be defined using case notation, which tells which functions to use as pieces and where to use them as pieces. The absolute value function, for example, can be written in case notation as follows:

$|x| = \begin{cases} x & \text{if } x \geq 0 \\ -x & \text{if } x < 0 \end{cases}$

This case notation just tells us that for negative inputs ($x<0$) we should use the function $y=-x$ to calculate the function output, and for nonnegative inputs ($x \geq 0$) we should use the function $y=x$ to calculate the function output.

Two more equivalent case notation forms for the absolute value function are shown below.

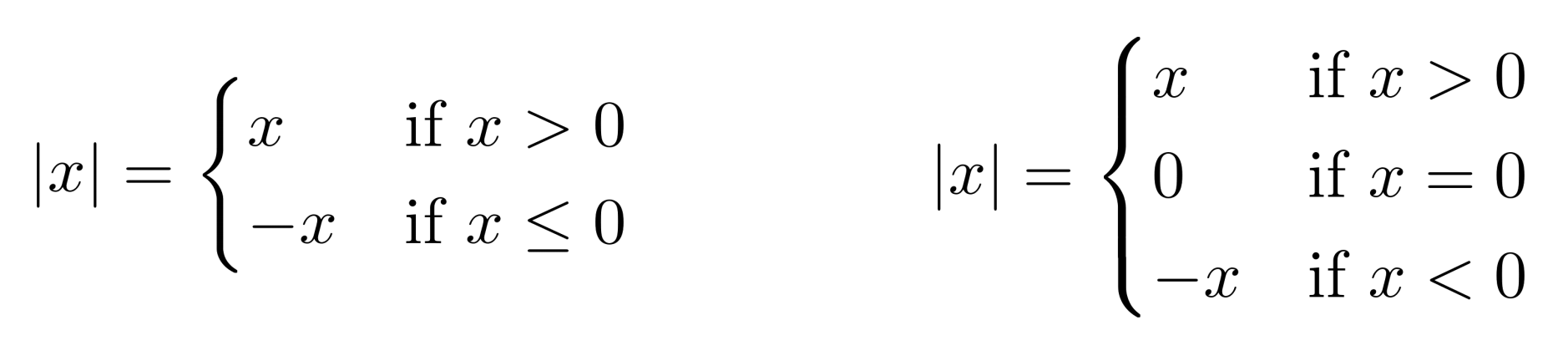
Sometimes, piecewise functions have breaks in them. For example, if we modify the case notation of the absolute value function so that the right piece is elevated, the graph has a break in it. This looks unusual, but it is a perfectly valid function.

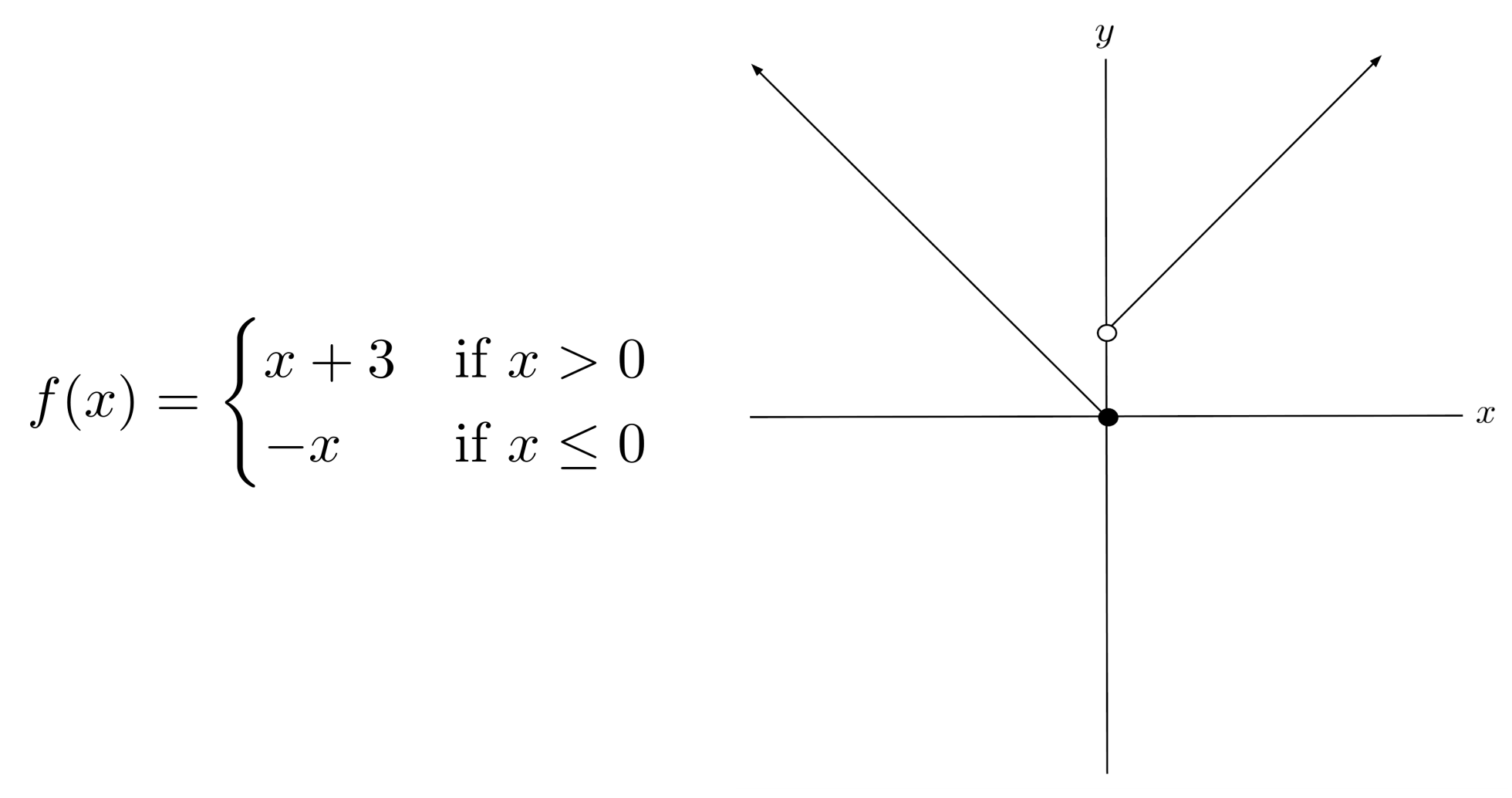
Many Function Types

There is no limit to what types of functions a piecewise function can consist of. For example, the equation and graph of a more complicated piecewise function are shown below.

$|x| = \begin{cases} \sin x & \text{if } x \geq 2 \\ \log_2 x & \text{if } 0 < x < 2 \\ x^2 & \text{if } -2 < x \leq 0 \\ x+8 & \text{if } x \leq -2 \end{cases}$

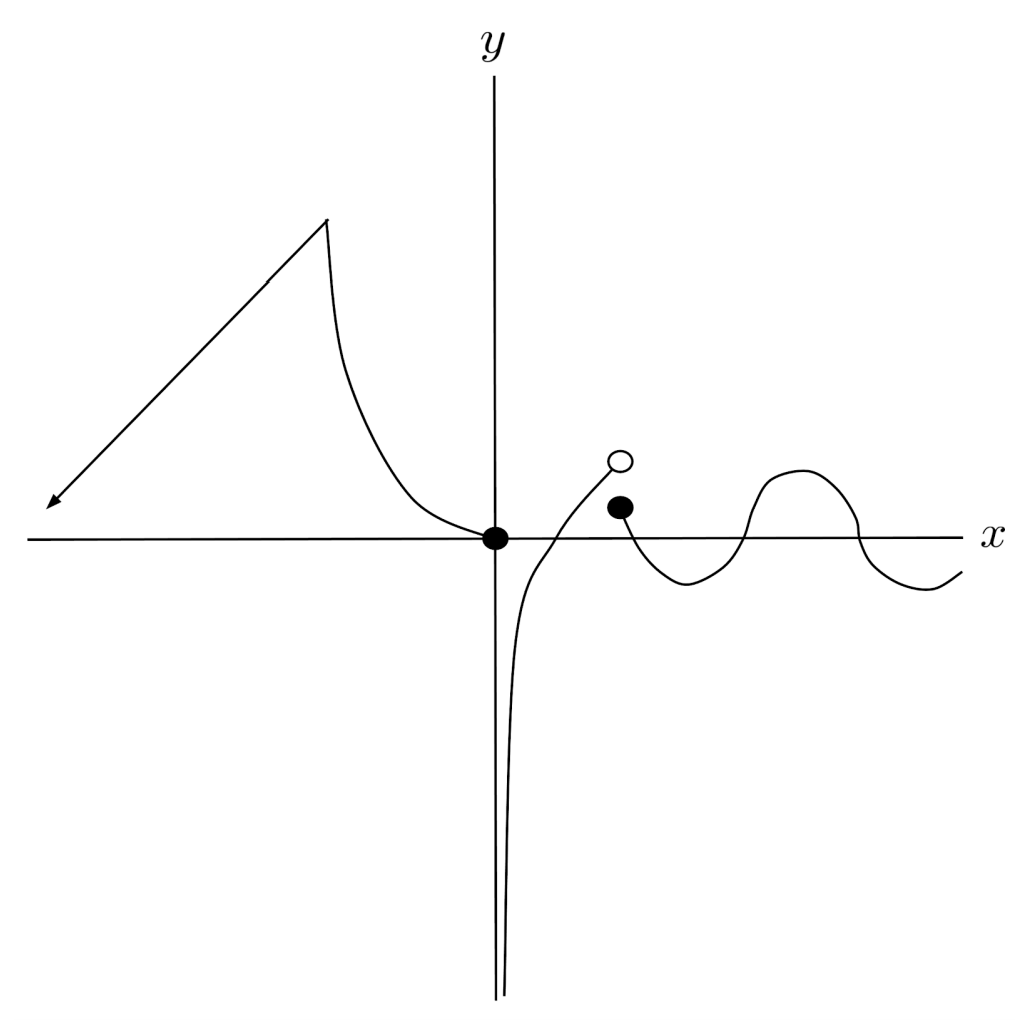
Many Cases

Likewise, there is no limit to the number of pieces a piecewise function can have. For example, rounding is an example of a piecewise function with infinitely many pieces.

$f(x) = \begin{cases} \vdots & \vdots \\ 2 &\mbox{if } 1.5 \leq x < 2.5 \\ 1 &\mbox{if } 0.5 \leq x < 1.5 \\ 0 &\mbox{if } -0.5 \leq x < 0.5 \\ -1 &\mbox{if } -1.5 \leq x < -0.5 \\ -2 &\mbox{if } -2.5 \leq x < -1.5 \\ \vdots & \vdots \end{cases}$

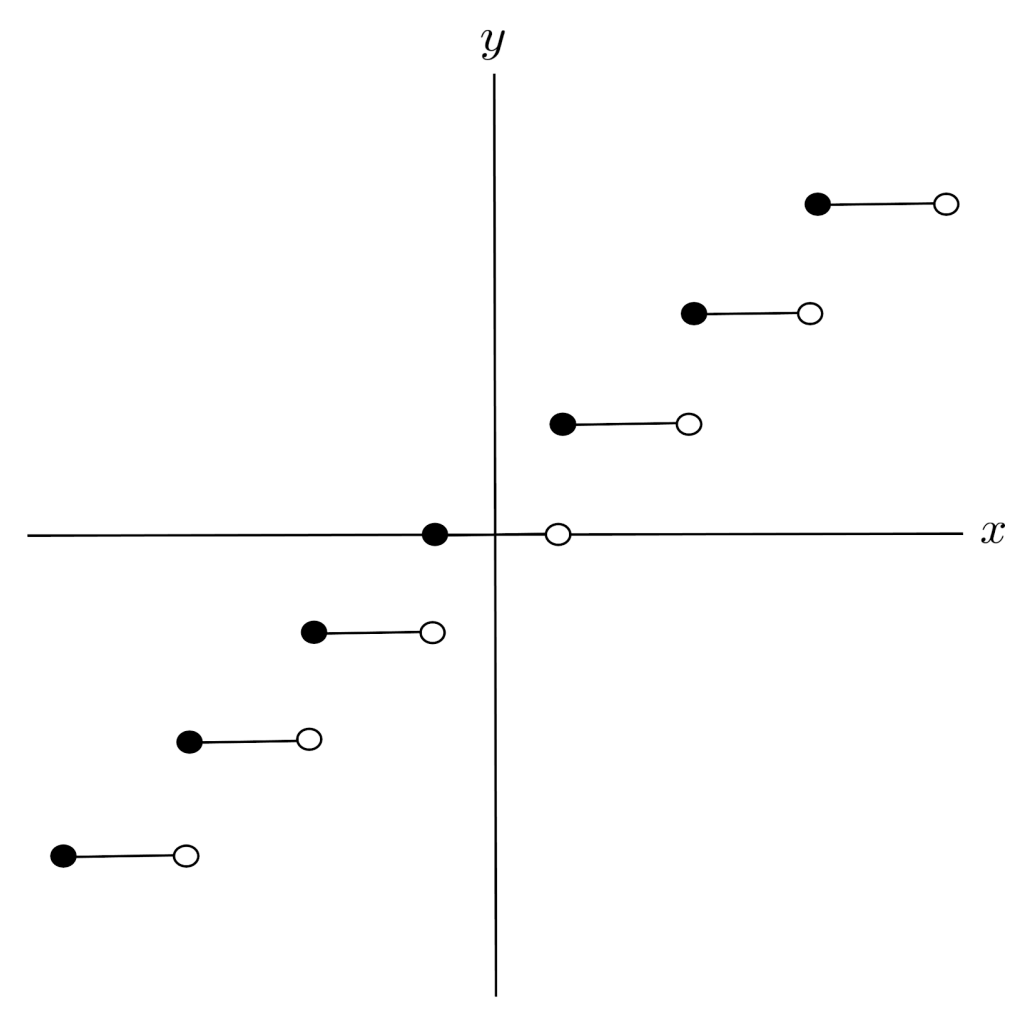
Exercises

Graph the following piecewise functions. (You can view the solution by clicking on the problem.)

$1) \hspace{.5cm} f(x)=\begin{cases} 2x & \text{if } x \geq 0 \\ \frac{1}{2}x &\text{ if} x < 0 \end{cases}$

Solution:

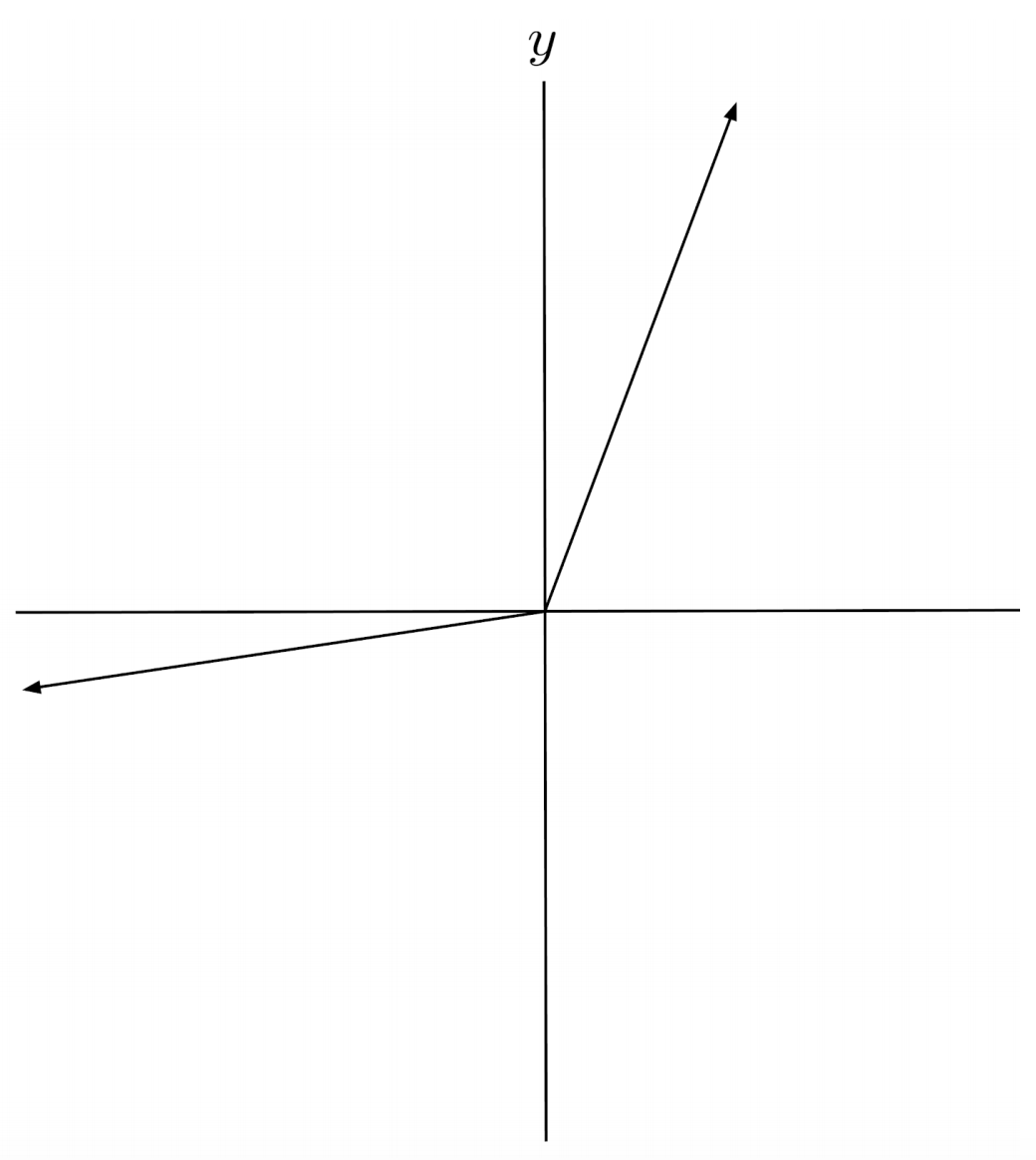
$2) \hspace{.5cm} f(x)=\begin{cases} x-5 & \text{if } x \geq 2 \\ x+5 &\text{ if} x < 2 \end{cases}$

Solution:

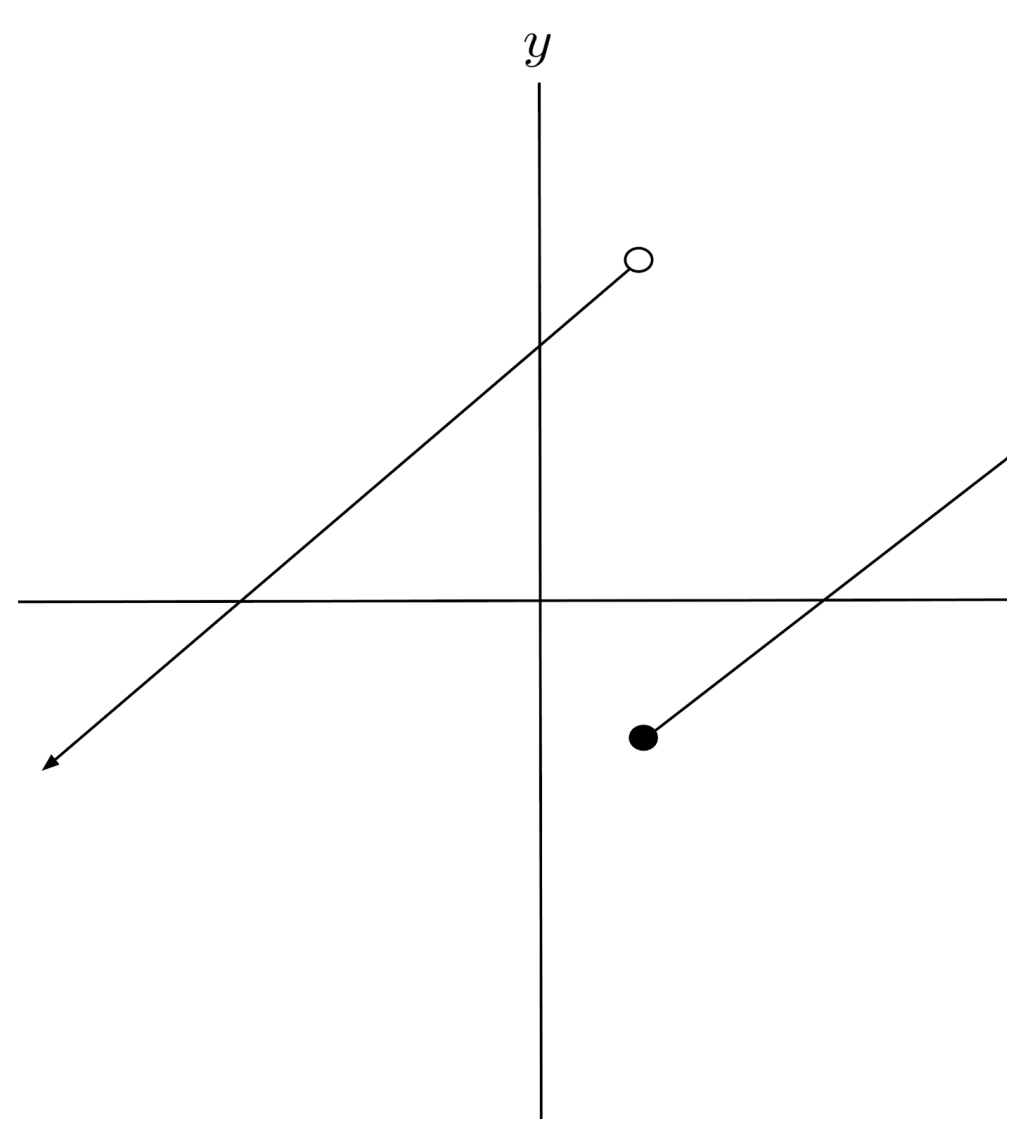
$3) \hspace{.5cm} f(x)=\begin{cases} x^2-4 & \text{if } x \geq 2 \\ 2-x &\text{if } 0 < x < 2 \\ x^2-4 &\text{if } x \geq 0 \end{cases}$

Solution:

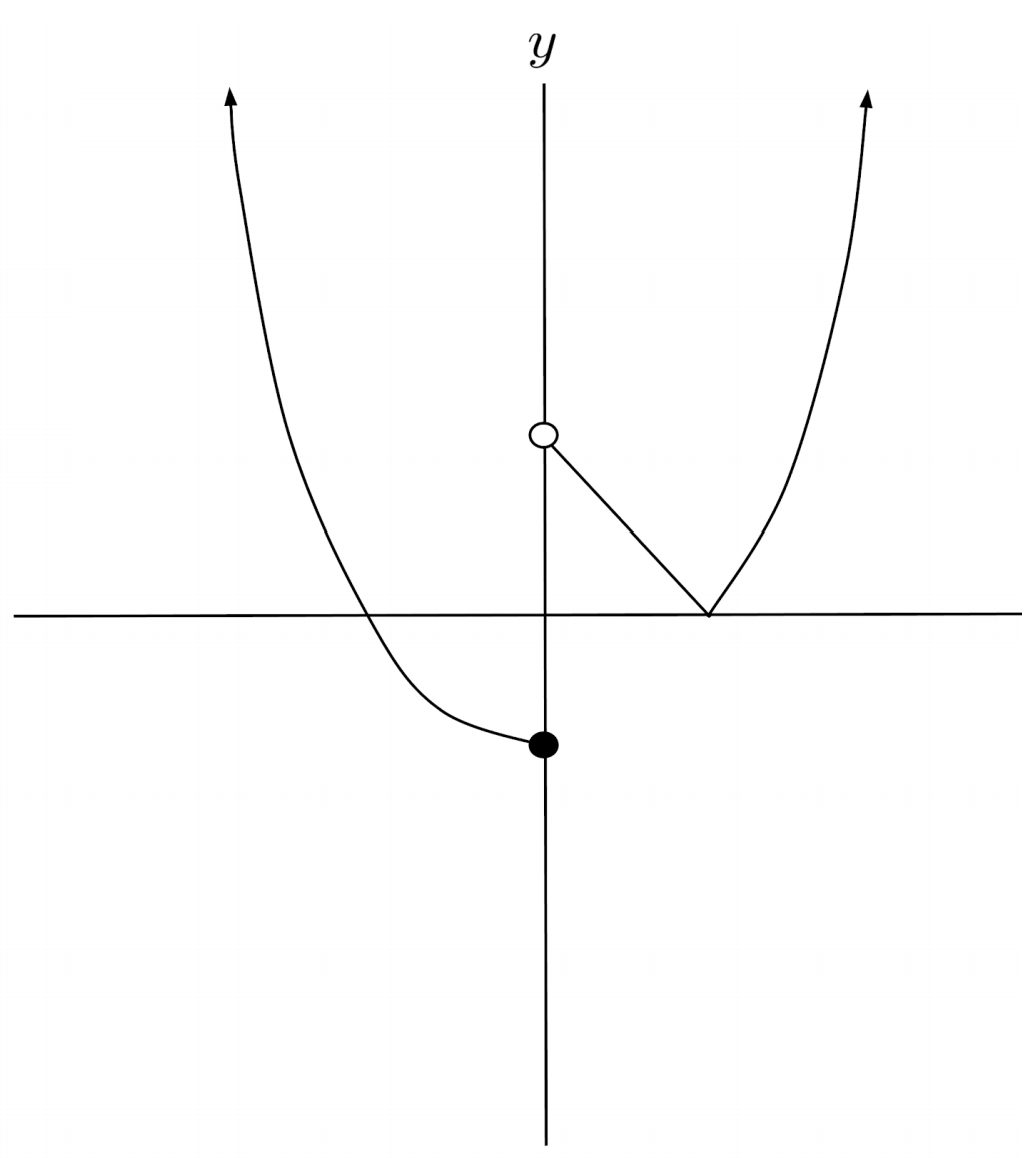
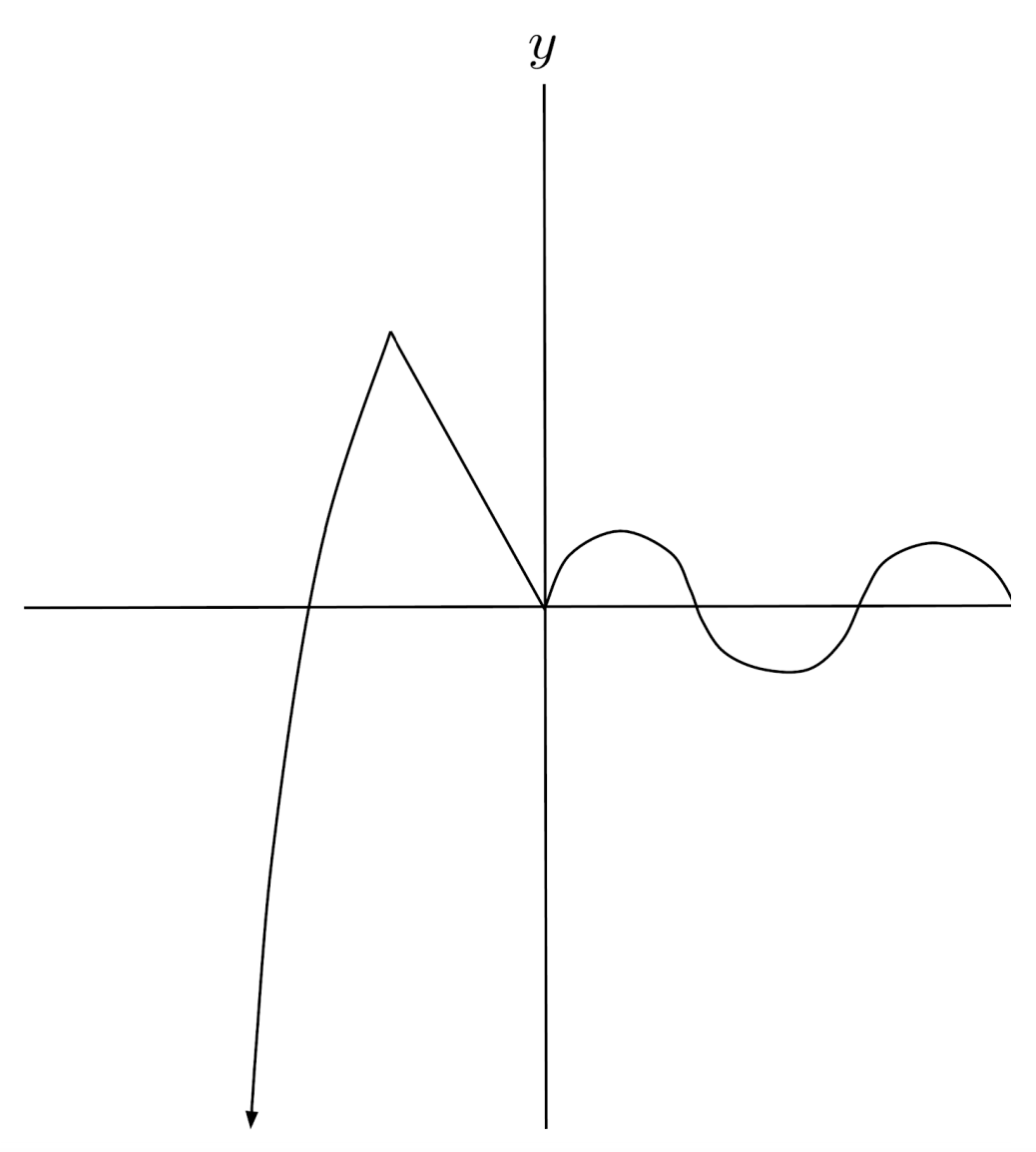
$4) \hspace{.5cm} f(x)=\begin{cases} \sin x &\text{if } x > 0 \\ -2x &\text{if } -2 < x \leq 0 \\ 8-x^2 &\text{if } x \leq -2 \end{cases}$

Solution:

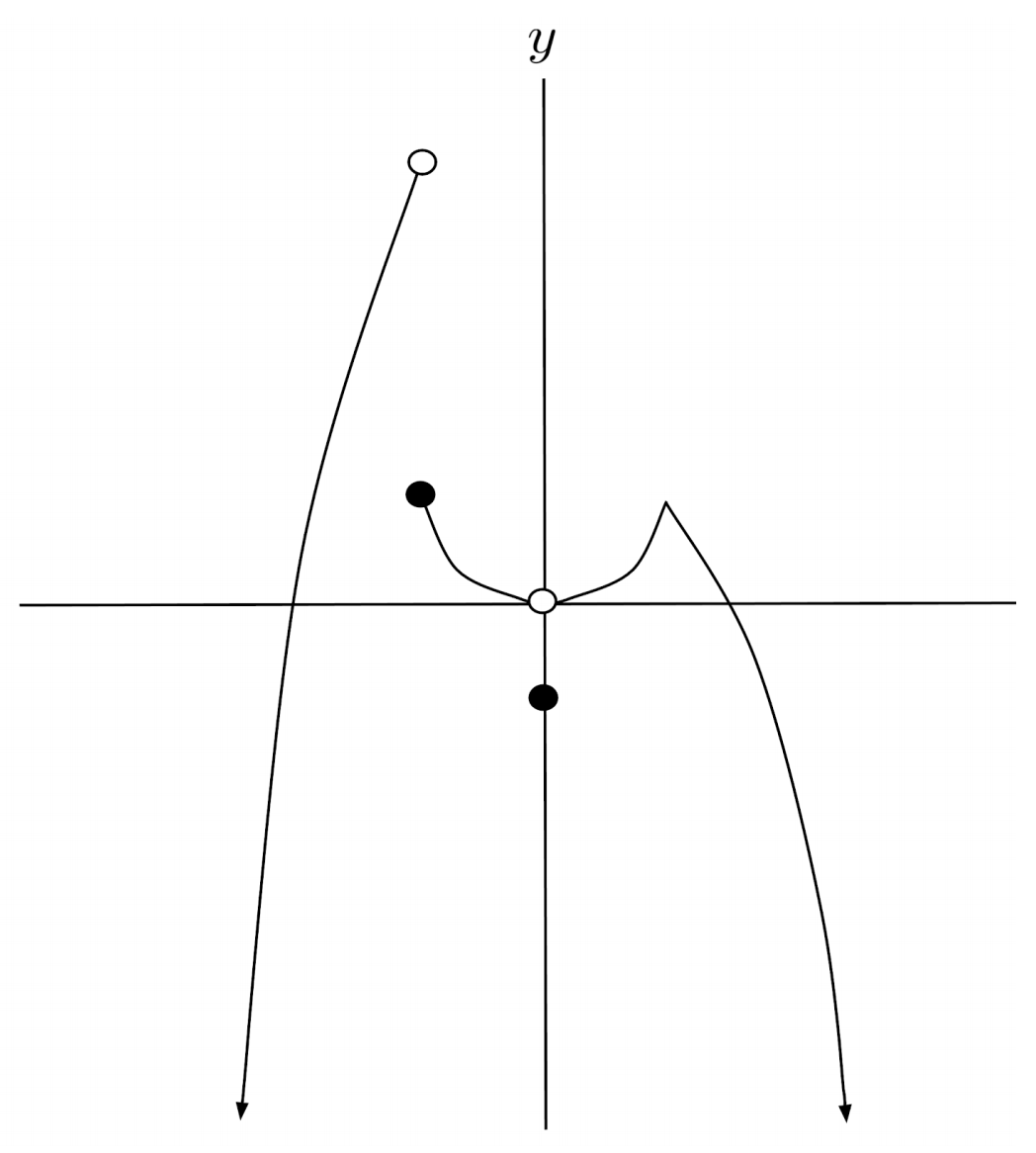
$5) \hspace{.5cm} f(x)=\begin{cases} 2-x^2 &\text{if } x \geq 1 \\ x^2 &\text{if } 0 < x < 1 \\ -1 &\text{if } x=0 \\ x^2 &\text{if } -1 \leq x < 0 \\ 8-x^2 &\text{if } x < -1 \end{cases}$

Solution:

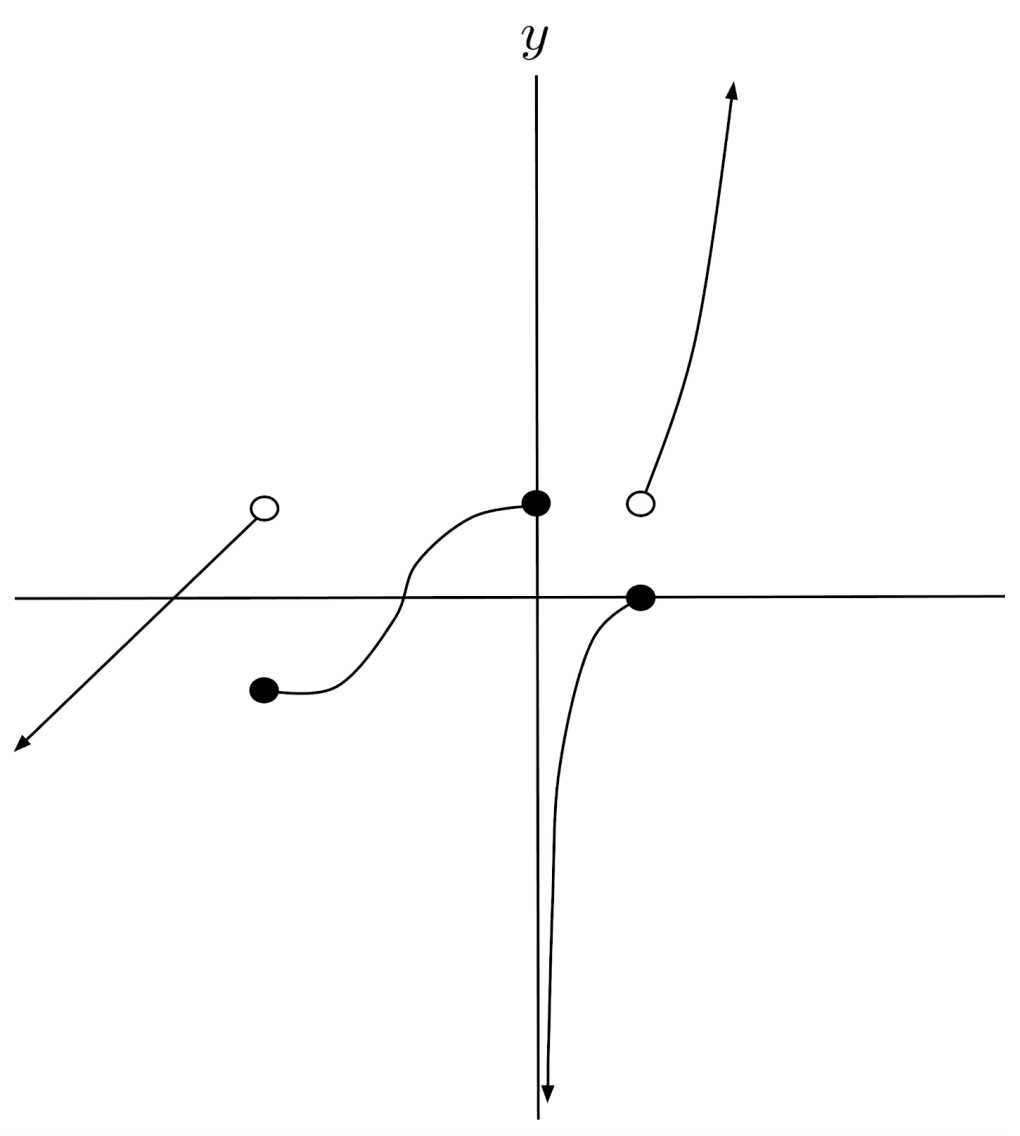
$6) \hspace{.5cm} f(x)=\begin{cases} x^2 &\text{if } x>1 \\ \log_2 x &\text{if } 0<x \leq 1 \\ \cos x &\text{if } -\pi \leq x \leq 0 \\ 4+x &\text{if } x < -\pi \end{cases}$

Solution:

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Piecewise Functions. In Justin Math: Algebra. https://justinmath.com/piecewise-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.