Path Dependency in Multivariable Limits

by Justin Skycak on December 04, 2019

The behavior of a multivariable function can be highly specific to the path taken.

The limit of a vector function is simply the limit of the vector’s components. For example, if $f(x,y,z) = \left< x^2y, \frac{x}{z} \right>,$ then

$\begin{align*} & \hspace{-.75cm} \lim\limits_{(x,y,z) \to (1,2,3)} f(x,y,z) \\[5pt] &= \lim\limits_{(x,y,z) \to (1,2,3)} \left< x^2y, \frac{x}{z} \right> \\[5pt] &= \left< \lim\limits_{(x,y,z) \to (1,2,3)} x^2y, \lim\limits_{(x,y,z) \to (1,2,3)} \frac{x}{z} \right> \\[5pt] &= \left< (1)^2(2), \frac{1}{3} \right> \\[5pt] &= \left< 2, \frac{1}{3} \right>. \end{align*}$

A Multivariable Limit that Does Not Exist

The limits above were easy to compute because we were able to perform direct substitution. However, multivariable limits become tricky when we have indeterminate limits.

For example, the limit below has indeterminate form of $\frac{0}{0}.$

$\begin{align*} \lim\limits_{(x,y) \to (0,0)} \frac{xy}{x^2+y^2} \to \frac{(0)(0)}{0^2+0^2} \to \frac{0}{0} \end{align*}$

One approach is to parameterize the limit to turn it into a single-variable limit – in single-variable calculus, we are able to simplify indeterminate limits using tools like L’Hopital’s rule.

For example, we might choose $x=t$ and $y=t,$ so that the limit as $(x,y) \to 0$ becomes the limit as $t \to 0.$ Under this parameterization, we find that the limit evaluates to $\frac{1}{2}.$

$\begin{align*} \lim\limits_{(x,y) \to (0,0)} \frac{xy}{x^2+y^2} &\to \lim\limits_{t \to 0} \frac{(t)(t)}{t^2+t^2} \\[5pt] &= \lim\limits_{t \to 0} \frac{t^2}{2t^2} \\[5pt] &= \lim\limits_{t \to 0} \frac{1}{2} \\[5pt] &= \frac{1}{2} \end{align*}$

But what if we used a different parameterization, say $x=t$ and $y=2t?$ We should get the same answer, right?

Unfortunately, this isn’t the case – under this second parameterization, we find that the limit comes out to a different result of $\frac{2}{5}.$

$\begin{align*} \lim\limits_{(x,y) \to (0,0)} \frac{xy}{x^2+y^2} &\to \lim\limits_{t \to 0} \frac{(t)(2t)}{t^2+(2t)^2} \\[5pt] &= \lim\limits_{t \to 0} \frac{2t^2}{5t^2} \\[5pt] &= \lim\limits_{t \to 0} \frac{2}{5} \\[5pt] &= \frac{2}{5} \end{align*}$

So, what gives? Is the limit $\frac{1}{2},$ or $\frac{2}{5},$ or something else that might be obtained under a different parameterization?

Because the limit comes out to different results for different parameterizations, we say that the limit does not exist.

Intuition

Let’s discuss this a bit more, from an intuitive standpoint. Intuitively, each parameterization represents a path through space:

the parameterization consisting of $x=t$ and $y=t$ follows the path $y=x,$ and
the parameterization consisting of $x=t$ and $y=2t$ follows the path $y=2x.$

So, the limit at some point can depend on the path we take to get there. We only say that a limit exists if it always maintains the same value, no matter which path we take to get there.

Checking All Linear Paths

Let’s do another example – this time, consider the function $g(x) = \frac{x^2y}{x^4+y^2}.$ Under the parameterization consisting of $x=t$ and $y=t,$ the limit comes out to $0.$

$\begin{align*} \lim\limits_{(x,y) \to (0,0)} \frac{x^2y}{x^4+y^2} &\to \lim\limits_{t \to 0} \frac{(t)^2(t)}{t^4+t^2} \\[5pt] &= \lim\limits_{t \to 0} \frac{t^3}{t^4+t^2} \\[5pt] &= \lim\limits_{t \to 0} \frac{t}{t^2+1} \\[5pt] &= \frac{0}{0+1} \\[5pt] &= 0 \end{align*}$

Likewise, under the parameterization consisting of $x=t$ and $y=2t,$ the limit comes out to $0$ again.

$\begin{align*} \lim\limits_{(x,y) \to (0,0)} \frac{x^2y}{x^4+y^2} &\to \lim\limits_{t \to 0} \frac{(t)^2(2t)}{t^4+(2t)^2} \\[5pt] &= \lim\limits_{t \to 0} \frac{2t^3}{t^4+4t^2} \\[5pt] &= \lim\limits_{t \to 0} \frac{2t}{t^2+4} \\[5pt] &= \frac{0}{0+4} \\[5pt] &= 0 \end{align*}$

We have a good feeling that this limit is $0$ regardless of the parameterization, but this is based only on the two paths $y=x$ and $y=2x.$ In order to verify that the limit is truly $0$ no matter how we approach it, we need to check all possible paths.

The easiest way to consider (almost) all linear paths at once is to use the parameterization $x=t$ and $y=mt,$ which corresponds to the path $y=mx.$ Then, provided $m \neq 0,$ we have

$\begin{align*} \lim\limits_{(x,y) \to (0,0)} \frac{x^2y}{x^4+y^2} &\to \lim\limits_{t \to 0} \frac{(t )^2(mt)}{(t)^4+(mt)^2} \\[5pt] &= \lim\limits_{t \to 0} \frac{mt^3}{t^4+m^2t^2} \\[5pt] &= \lim\limits_{t \to 0} \frac{mt}{t^2+m^2} \\[5pt] &= \frac{m(0)}{(0)^2 +m^2} \\[5pt] &= 0. \end{align*}$

If $m=0,$ then we have the parameterization $x=t$ and $y=0,$ in which case the limit also evaluates to $0.$

$\begin{align*} \lim\limits_{(x,y) \to (0,0)} \frac{x^2y}{x^4+y^2} &\to \lim\limits_{t \to 0} \frac{(t )^2(0)}{(t)^4+(0)^2} \\[5pt] &= \lim\limits_{t \to 0} 0 \\[5pt] &= 0 \end{align*}$

That covers all lines of the form $y=mx.$ The only remaining line to check is $x=0,$ which can be parameterized as $x=0$ and $y=t.$ In this case, too, the limit also evaluates to $0{:}$

$\begin{align*} \lim\limits_{(x,y) \to (0,0)} \frac{x^2y}{x^4+y^2} &\to \lim\limits_{t \to 0} \frac{(0 )^2(t)}{(0)^4+(t)^2} \\[5pt] &= \lim\limits_{t \to 0} 0 \\[5pt] &= 0 \end{align*}$

We can conclude that the limit is $0$ on all linear paths.

Checking All Linear Paths is Not Good Enough

Although the limit is $0$ on all linear paths, this is not enough to conclude that the limit is truly $0$ from all paths – there are nonlinear paths as well.

Your intuition might tell you that if the limit goes to $0$ on all linear paths, then it must surely go to $0$ on all paths – but surprisingly, this would not be correct.

For example, on the quadratic path $y=x^2,$ which is parameterized by $x=t$ and $y=t^2,$ the limit comes out to $\frac{1}{2}.$

$\begin{align*} \lim\limits_{(x,y) \to (0,0)} \frac{x^2y}{x^4+y^2} &\to \lim\limits_{t \to 0} \frac{(t )^2(t^2)}{(t)^4+(t^2)^2} \\[5pt] &= \lim\limits_{t \to 0} \frac{t^4}{t^4+t^4} \\[5pt] &= \lim\limits_{t \to 0} \frac{t^4}{2t^4} \\[5pt] &= \lim\limits_{t \to 0} \frac{1}{2} \\[5pt] &= \frac{1}{2} \end{align*}$

So, the limit doesn’t exist.

You might be wondering how it’s possible for the limit to be $0$ from every linear path, but $\frac{1}{2}$ on a quadratic path – the graph below should provide some intuition.

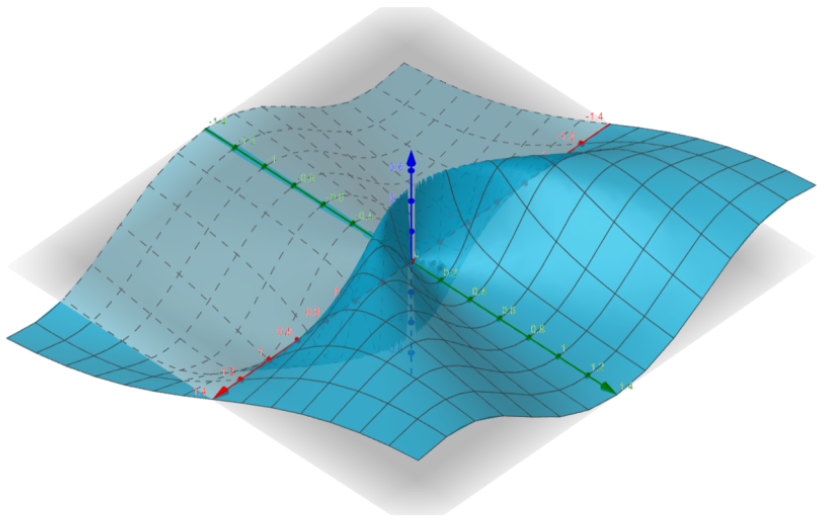
The lesson learned here is that the behavior of a multivariable function can be highly specific to the path taken.