Linear Inequalities in the Number Line

An inequality is similar to an equation, but instead of saying two quantities are equal, it says that one quantity is greater than or less than another.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Linear Inequalities in the Number Line. In Justin Math: Algebra. https://justinmath.com/linear-inequalities-in-the-number-line/

Want to get notified about new posts? Join the mailing list.

An inequality is similar to an equation, but instead of saying two quantities are equal, it says that one quantity is greater than or less than another.

For example, since $1$ is greater than $0$, we write $1>0$. Likewise, since $0$ is less than $1$, we write $0<1$.

If we write $x>0$, then we mean that $x$ can be $1$, $2$, $\pi$, $0.000001$, or any other positive number. If we write $x<0$, then we mean that $x$ can be $-1$, $-2$, $-\pi$, $-0.000001$, or any other negative number.

"Or Equal To" Inequalities

We can also write $x \geq 0$ to mean that $x$ is greater than or equal to $0$.

In $x>0$, the number $0$ is not a valid solution for $x$ because $0$ is not greater than $0$, but in $x \geq 0$, the number $0$ is a valid solution because $0$ is greater than or equal to $0$.

Likewise, we can write $x \leq 0$ to mean that $x$ is less than or equal to $0$.

Solving Inequalities

Inequalities can be solved much like equations: we can perform algebraic manipulations to both sides of the equation until we isolate the variable.

If we substitute any number that is greater than $5$, it will satisfy the original inequality.

For example, if we substitute $x=6$, then the original inequality becomes $22>20$, which is true. Likewise, if we substitute $x=5.001$, then the original inequality becomes $18.004>18.002$, which is true.

On the other hand, if we substitute any number that is $5$ or less, it will not satisfy the original inequality.

For example, if we substitute $x=5$, then the original inequality becomes $18>18$, which is not true. Likewise, if we substitute $x=4$, then the original inequality becomes $14>16$, which is not true.

Flipping the Inequality

In manipulating inequalities, there is just one catch: whenever we multiply or divide by a negative number, we have to flip the inequality.

To understand why we need to flip the inequality whenever we multiply or divide by a negative sign, consider the example $1<2$. If we multiply or divide by $-1$, we reach $-1<-2$, which is not true. In order to keep the inequality true, we have to flip the inequality sign: $-1>-2$.

Plotting Inequalities

To visualize inequalities, we can plot them on a number line. An open (unfilled) circle around a point means that the point itself is NOT a solution, while a closed (filled) circle around a point means that the point itself is a solution.

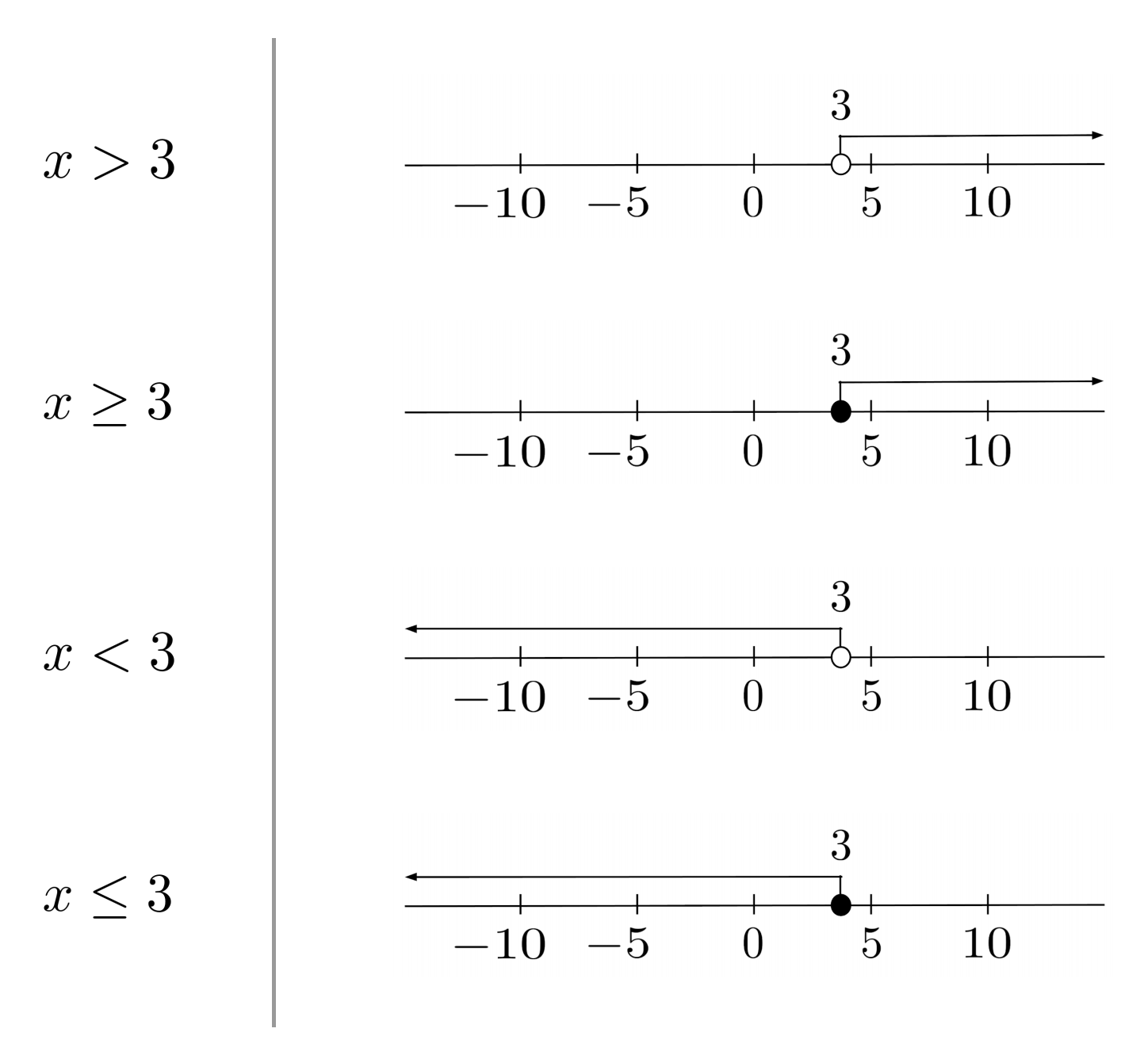
Interval Notation

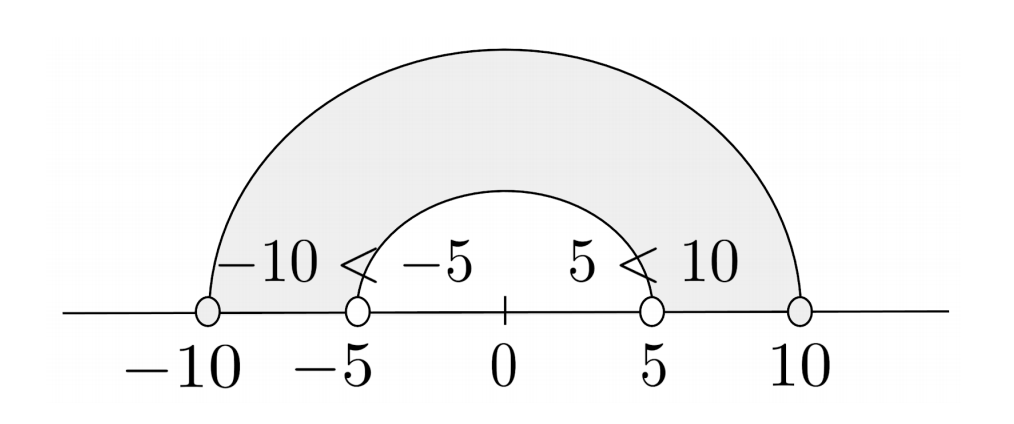
The number line can help us understand why we have to flip the inequality sign whenever we multiply or divide by a negative number.

Starting with $5<10$, we know that $10$ is the bigger number that is further from $0$. When we multiply or divide, $10$ is still going to be further from $0$ than $5$ is – but if we multiply or divide by a negative number, then $10$ will be further from $0$ in the negative direction, which means it will actually be the lesser number.

The number line is a great intuitive aid, but it takes a while to draw. To simultaneously leverage the benefit of number line intuition and avoid the headache of drawing actual number lines, it is common to use interval notation, which represents number line segments using parentheses for open circles and brackets for closed circles.

To indicate that a segment continues forever, we imagine it having an open circle at positive or negative infinity.

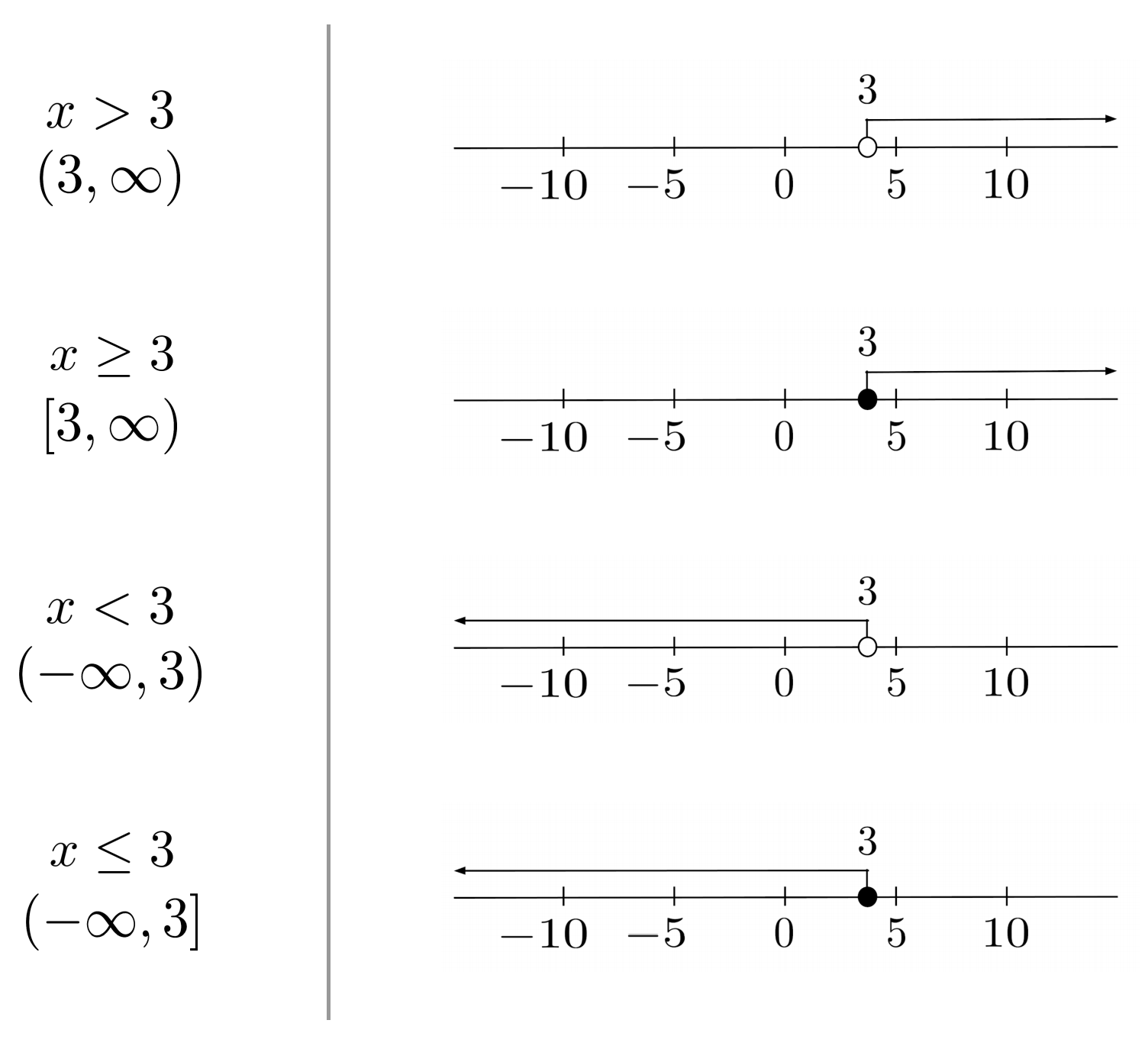
Exercises

Solve the following inequalities, writing the solutions in interval notation. (You can view the solution by clicking on the problem.)

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Linear Inequalities in the Number Line. In Justin Math: Algebra. https://justinmath.com/linear-inequalities-in-the-number-line/

Want to get notified about new posts? Join the mailing list.