Intuiting Series

A series is the sum of a sequence.

This post is part of the series An Intuitive Primer on Calculus.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

A series is the sum of a sequence. For example, for the sequence of even numbers from $0$ to $10,$ the series is given by

It would make no sense if we tried to add up infinitely many of the even numbers, but sometimes it is actually possible to add up infinitely many numbers and still get a sensible answer.

For example, consider the series $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\ldots,$ where the next term is always half the preceding term.

Each time we add the next term in the sequence, it’s like shading in half of what’s left in the whole circle. The more numbers we add, the closer we get to filling in the whole circle.

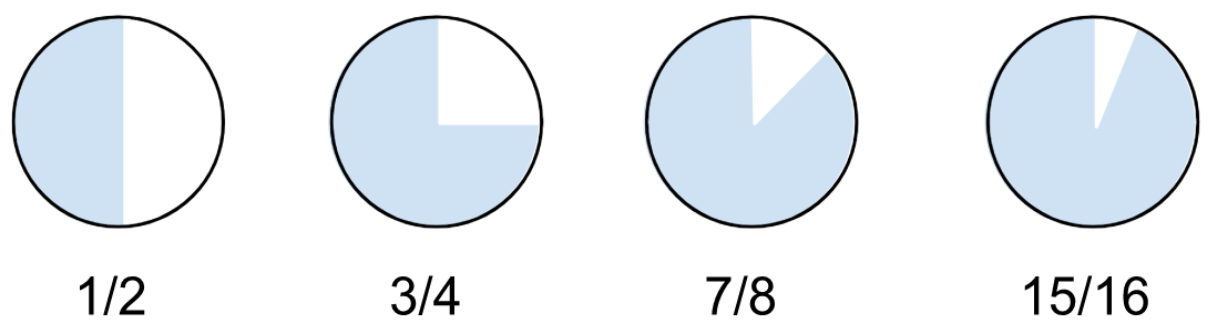
Since we get closer and closer to filling in the whole circle as the series goes on, we say that the series converges to $1.$ The takeaway of this example is that when terms in a series get small enough fast enough, their sum might not be infinite.

It’s easy to see that series only make sense when the terms converge to zero (otherwise, you could surpass any number by summing enough terms). However, just because a series’ terms converge to zero, does not necessarily mean that you can add them all up and get a finite answer. For example, the series $\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\ldots$ sums to infinity, or diverges.

It is often difficult to tell whether a series converges or diverges just by looking at it. However, there are some tests you can apply to a series to tell whether it converges or diverges. Many of these tests involve computing limits or integrals.

This post is part of the series An Intuitive Primer on Calculus.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.