Intuiting Naive Bayes

by Justin Skycak (@justinskycak) on

Naive Bayes classification naively assumes that the presence of a particular feature in a class is unrelated to the presence of any other feature.

This post is part of the series Intuiting Predictive Algorithms.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

If we know the causal structure between variables in our data, we can build a Bayesian network, which encodes conditional dependencies between variables via a directed acyclic graph. Such a model is constrained by our human understanding of the relationship between parts of the data, though, and may not be optimal when we wish to predict a target variable despite knowing little about the other variables to which it may or may not relate.

That being said, if we know that the target variable is a class that somehow encapsulates the other variables, it can be worthwhile to try a Bayesian network where the other variables are assumed to depend conditionally and independently on the class. This is called Naive Bayes classification because it naively assumes that the presence of a particular feature in a class is unrelated to the presence of any other feature.

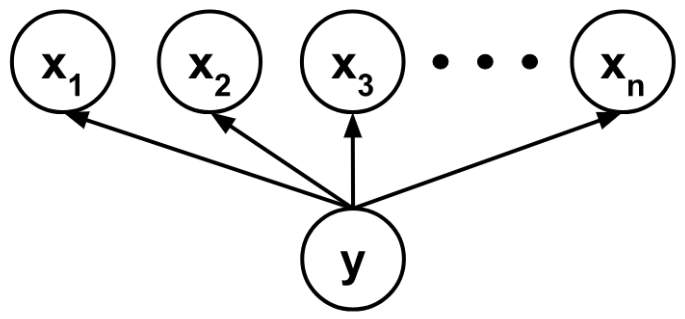
image


If the data is given by $\lbrace ((x_{ij}), y_i) \rbrace$ and each $y_i$ belongs to a class $C_k,$ then the Naive Bayes classifier computes

$\begin{align*} C_k &= \arg\max_{C_k} P(C_k|x) \\[5pt] &= \arg\max_{C_k}\frac{P(x|C_k)P(C_k)}{P(x)} \\[5pt] &= \arg\max_{C_k} P(x|C_k)P(C_k) \\[5pt] &= \arg\max_{C_k} P(C_k) \prod_j P(x_j|C_k) \end{align*}$


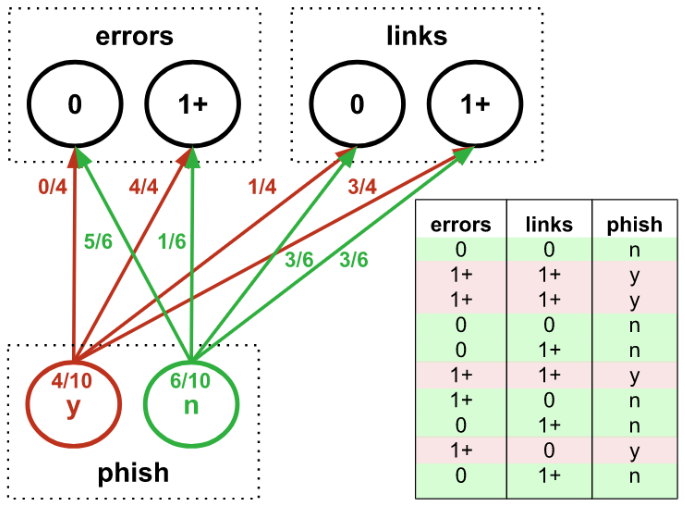
For example, we could build a Naive Bayes classifier to predict whether an email is a phishing attempt based on whether it has spelling errors and links:

image


We could then use our model to test whether a new email is a phishing attempt:

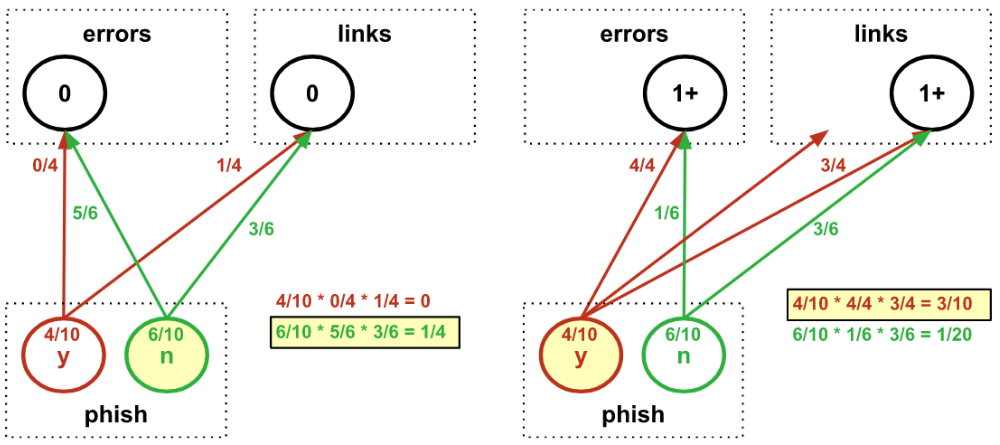
image


In this example, we used discrete bins for the features – but Naive Bayes can also handle features that are fit to continuous distributions. And despite assuming that features are independent (and thus potentially ignoring a lot of useful information), Naive Bayes can sometimes perform well enough in simple applications to get the job done.

This post is part of the series Intuiting Predictive Algorithms.


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.