Intuiting Integrals

by Justin Skycak (@justinskycak) on

Integrals give the area under a portion of a function.

This post is part of the series An Intuitive Primer on Calculus.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Integrals give the area under a portion of a function. For example, for the function $y=2x,$ the integral from $x=0$ to $x=2,$ written

$\begin{align*} \displaystyle\int_0^2 2x \, dx, \end{align*}$


is the area of the resulting triangle,

$\begin{align*} \frac{1}{2}(base)(height) = \frac{1}{2}(2)(4) = 4. \end{align*}$


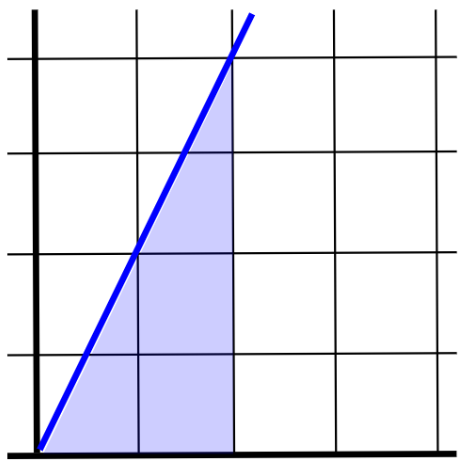
image


That integral was easy to compute, because we already knew the formula for area of a triangle. But what if we wanted to calculate the area of a curvy function like $x^2,$ where we don’t have a formula for the area?

One way to proceed is to approximate the area by breaking it into a bunch of rectangles and adding up the areas of all the rectangles. The more rectangles, the better the approximation.

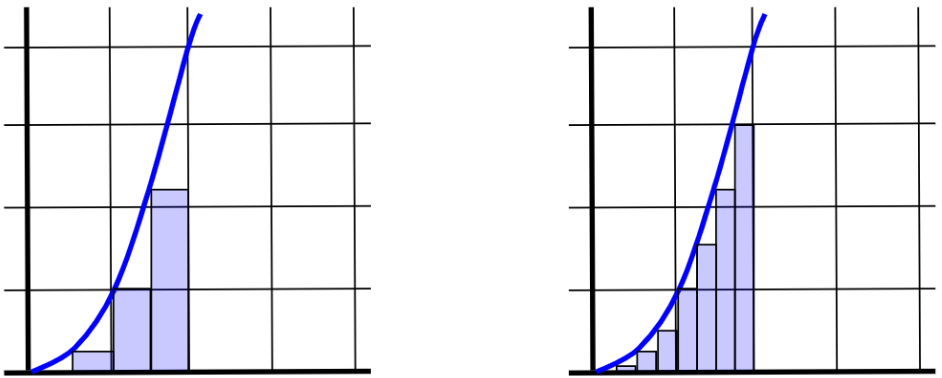
image


It turns out that taking the limit of infinitely many rectangles reveals a slick trick to get the exact area. To use this trick on the function $x^2,$ we need only follow three steps:

  1. Work backwards to find the function whose derivative is $x^2$ (it's $\frac{1}{3} x^3$).
  2. Evaluate $\frac{1}{3} x^3$ at $x=0$ and $x=2$ (to get $0$ and $\frac{8}{3}$).
  3. Take the difference (to get $\frac{8}{3}$).

The toughest part of the process is usually the first step, which involves working backwards to find the opposite of the derivative, called the antiderivative. However, there are rules we can use to complete this step quickly.

For example, the power rule says that the integral of any function $x^n,$ where $n$ is some number, is $\frac{1}{n+1} x^{n+1}.$ That is,

$\begin{align*} \displaystyle\int x^n \, dx = \frac{1}{n+1} x^{n+1}. \end{align*}$


You can verify that this rule is true because if you differentiate the function $\frac{1}{n+1} x^{n+1},$ you get $\frac{1}{n+1}(n+1)x^n,$ which comes out to just $x^n.$

There are other rules as well, for different types of functions.

This post is part of the series An Intuitive Primer on Calculus.


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.