Intuiting Functions

by Justin Skycak (@justinskycak) on

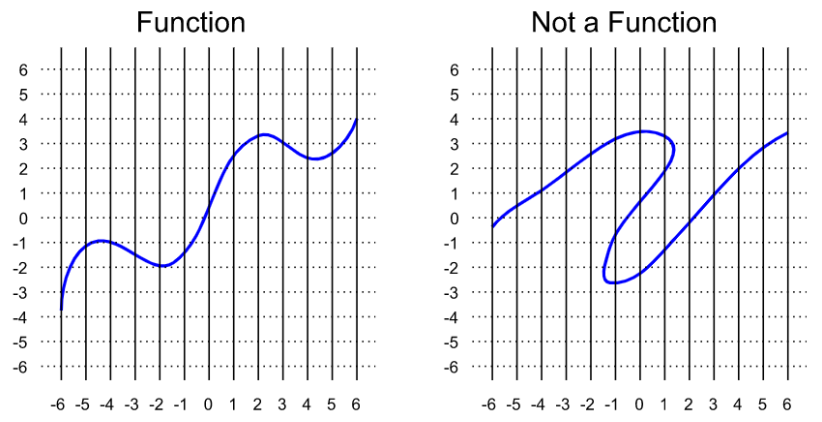
A function is a scribble that crosses each vertical line only once.

This post is part of the series An Intuitive Primer on Calculus.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

A function is a scribble that crosses each vertical line only once.

image


The instructions for drawing a function are given by the function’s equation. Each vertical line is labeled with a number, and when you plug that number into the $x$ variable in a function, the result tells you how high the function should be when it crosses that line.

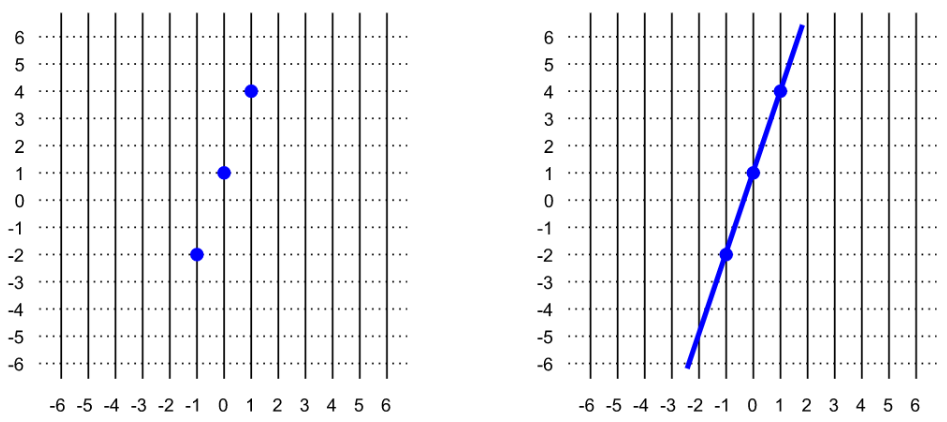
For example, to draw the function whose equation is $y=3x+1$, we can start by plugging in the numbers $-1,$ $0,$ and $1.$

$\begin{align*} x=-1 \Longrightarrow y&=3(-1)+1=-2 \\[5pt] x=0 \Longrightarrow y&=3(0)+1=1 \\[5pt] x=1 \Longrightarrow y&=3(1)+1=4 \end{align*}$


Our results mean:

  • On the line $x=-1,$ the scribble needs to cross at height $y=-2.$
  • On the line $x=0$, the scribble needs to cross at height $y=1.$
  • On the line $x=1,$ the scribble needs to cross at height $y=4.$

In other words, we need to plot the points $(-1,-2),$ $(0,1),$ and $(1,4)$ on the grid. Since this is a linear function, we can draw the rest of the function just by connecting the dots.

image


Linear functions are straight lines, but in general, functions tend to be curvy. There are many different types of functions, each of whose scribble curves in a different way.

This post is part of the series An Intuitive Primer on Calculus.


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.