Intuiting Derivatives
The derivative tells the steepness of a function at a given point, kind of like a carpenter's level.
This post is part of the series An Intuitive Primer on Calculus.
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.
The derivative tells the steepness of a function at a given point, kind of like a carpenter’s level. For example, the derivative of a flat function is $0$ because the bubble doesn’t move when you hold up a level to the function:
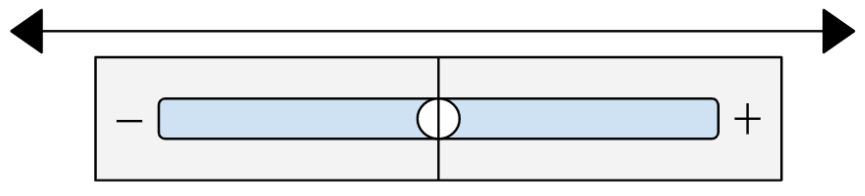
However, if you hold up a level to a function that inclines upward, the bubble will move right, to a positive number. How big this positive number is, depends on how steeply the function is inclined. If the function is only a slight incline, like a wheelchair ramp, then the derivative will be small. However, if the function is steeply inclined, like a mountainside, then the derivative will be large.
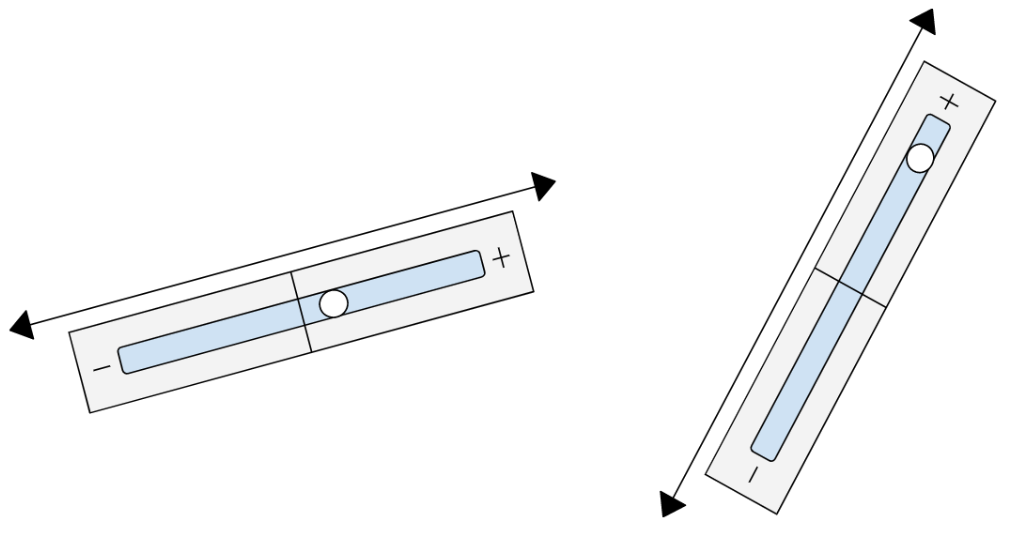
Likewise, if you use a level to measure the derivative of a function that declines downward, the bubble will move left, to a negative number. Functions that are slightly declined will have slightly negative derivative, and functions that are steeply declined will have extremely negative derivative.
Now that we understand the intuition behind the derivative, we can offer a more precise definition: the derivative is the distance upward, per unit of distance horizontal. For example, if you walk to the right one meter on a hill, you might go up two meters, so the derivative is $2.$
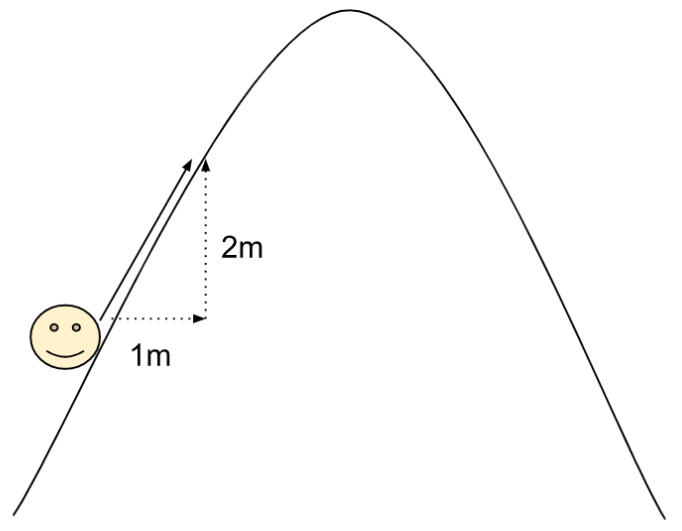
The way to compute this mathematically is to start at your initial point, pick a point that’s really close to it, compute the change in vertical distance, and then divide by the change in horizontal distance.
For example, in the function \(y=x^2\), if we want to compute the derivative at the point \((2,4)\), we can pick a nearby point \((3,9)\) and compute the slope:
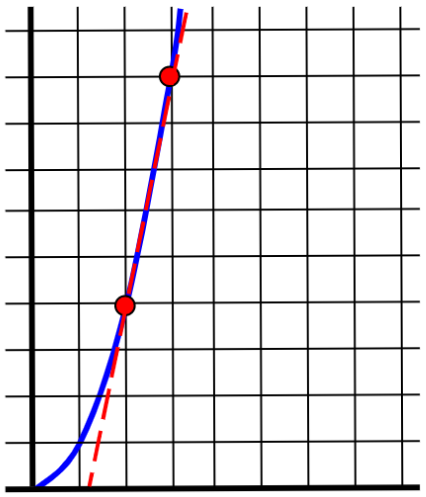
This isn’t exactly right, but it’s a good ballpark estimate. We can get a better estimate by picking a point that’s even closer to the initial point: the slope between $(2,4)$ and $(2.1,4.41)$ is
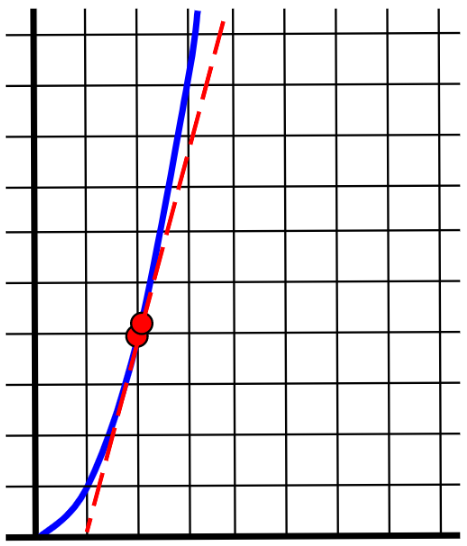
And if we move the point even closer, then we get an even better approximation: the slope between $(2,4)$ and $(2.01, 4.0401)$ is
Given our increasingly accurate approximations of $5,$ $4.1,$ and $4.01,$ you can probably guess that the exact derivative is $4.$ That is to say, the limit of the slope is $4,$ since the closer we move our second point, the closer the slope between the two points gets to $4.$
It would be frustrating if we always had to guess the exact derivative by making approximations first. Conveniently, there are rules we can use to calculate the exact derivative quickly.
For example, the power rule says that if you have a function $x^n$ for some number $n,$ the derivative is $nx^{n-1}.$ Symbolically, that’s written
In the previous example,
meaning that the derivative of $x^2$ is $2x.$ We wanted to find the derivative when $x=2,$ so we plug in $2$ to the derivative to get $2(2)=4.$
There are other rules as well, for different types of functions.
This post is part of the series An Intuitive Primer on Calculus.
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.