Q&A: How Can Geometric Approaches be Used When Teaching Algebra?

by Justin Skycak (x.com/justinskycak) on

Cross-posted from here.

Want to get notified about new posts? Join the mailing list.

In my experience,

  • geometry can lead you into interesting questions that can be answered geometrically in special cases, and
  • algebra can help you tighten up the rigor of your answers and generalize your results.

For instance, here’s an example of how I would combine geometric and algebraic approaches to teach an algebraic concept. I’ll illustrate on a simple concept, expanding binomials.


1. Motivate the end result using geometric intuition.

The quantity $(a+b)^2$ represents the area of a square with side length $a+b.$ Draw a picture of said square…

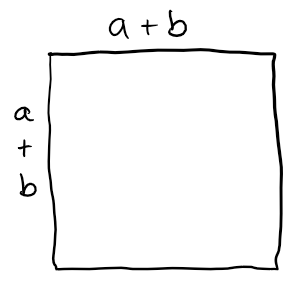
image


…and illustrate how it can be partitioned into

  • $2$ squares of dimensions $a \times a$ and $b \times b,$ and
  • $2$ rectangles of dimensions $a \times b$ and $b \times a.$
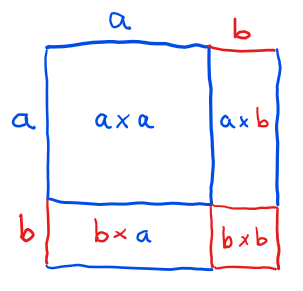
image


This would suggest that

$$\begin{align*} (a+b)^2 &= a^2 + b^2 + ab + ba \\ &= a^2 + 2ab + b^2. \end{align*}$$


2. Tighten up the rigor using algebra.

Sure, this picture makes sense when $a$ and $b$ are positive numbers. But what about if $a$ or $b$ is zero or negative?

Granted, if we come up with a situation like that and plug it into our formula, the formula seems to come out to a true statement. But how can we be sure it will always work? And how can we make sense of the fact that it does in fact still work?

To answer these questions, we observe that the same result can be obtained by writing the exponentiation as a multiplication and then applying the distributive property:

$$\begin{align*} (a+b)^2 &= (a+b)(a+b) \\ &= a(a+b) + b(a+b) \\ &= a^2 + ab + ba + b^2 \\ &= a^2 + 2ab + b^2 \quad \checkmark \end{align*}$$


3. Demonstrate the utility of algebra.

What if we wanted to compute $(a+b)^3,$ or $(a+b)^4,$ or a higher power? It’s tricky to draw a picture of a cube, and impossible to draw a picture of a cube with $4$ or more dimensions. What do we do?

We just use the algebraic approach:

$$\begin{align*} (a+b)^3 &= (a+b)(a+b)^2 \\ &= (a+b)(a^2+2ab+b^2) \\ &= a(a^2+2ab+b^2) + b(a^2+2ab+b^2) \\ &= a^3 + 2a^2b + b^2 + ba^2 + 2ab^2 + b^3 \\ &= a^3 + 3a^2b + 3ab^2 + b^3 \end{align*}$$



Want to get notified about new posts? Join the mailing list.