Graphing Rational Functions with Slant and Polynomial Asymptotes
A slant asymptote is a slanted line that arises from a linear term in the proper form of a rational function.
This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Graphing Rational Functions with Slant and Polynomial Asymptotes. In Justin Math: Algebra. https://justinmath.com/graphing-rational-functions-with-slant-and-polynomial-asymptotes/
A horizontal asymptote is a horizontal line that arises from a constant whole number term in the proper form of a rational function.
Likewise, a slant asymptote is a slanted line that arises from a linear term in the proper form of a rational function.
Demonstration
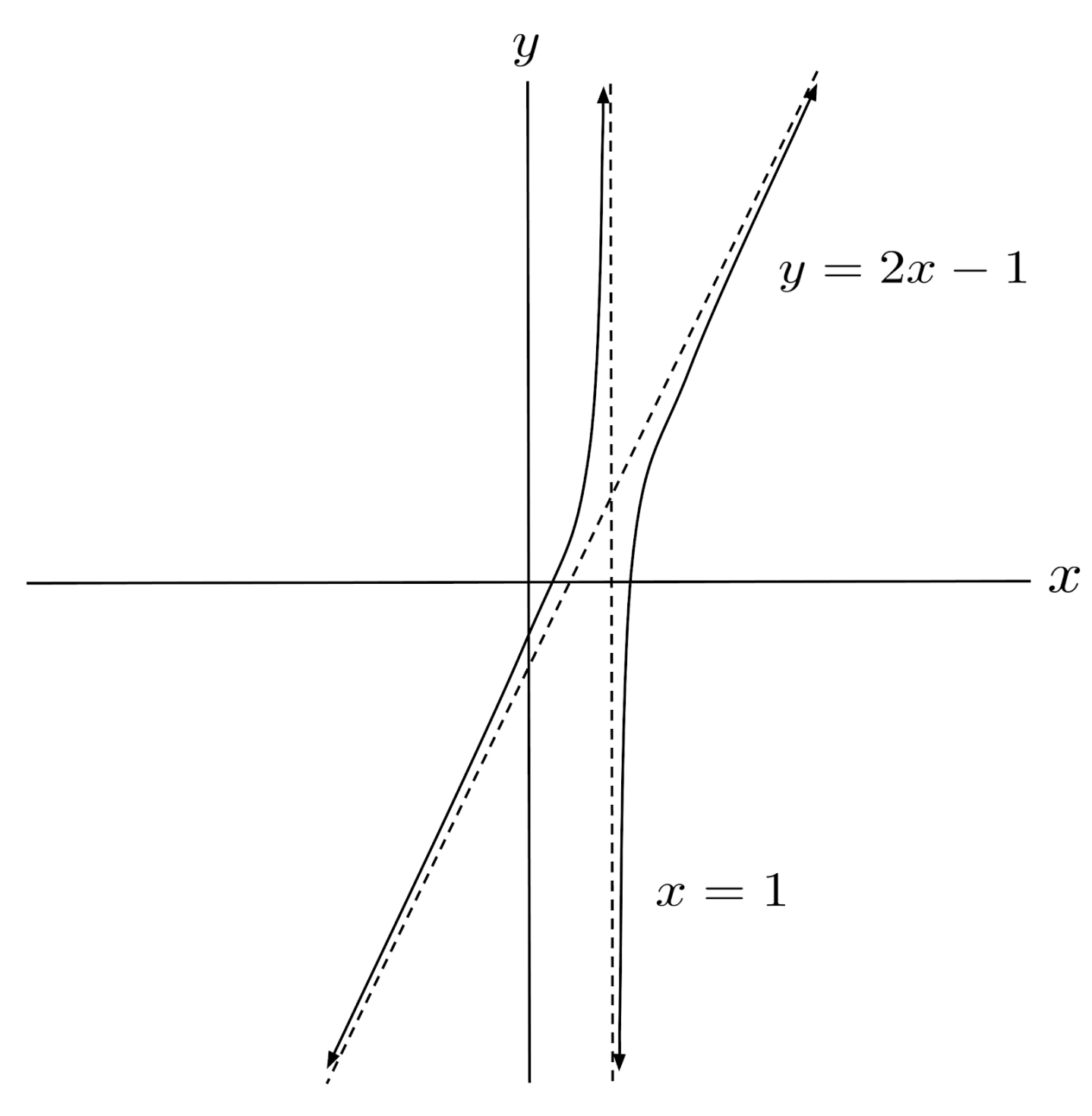
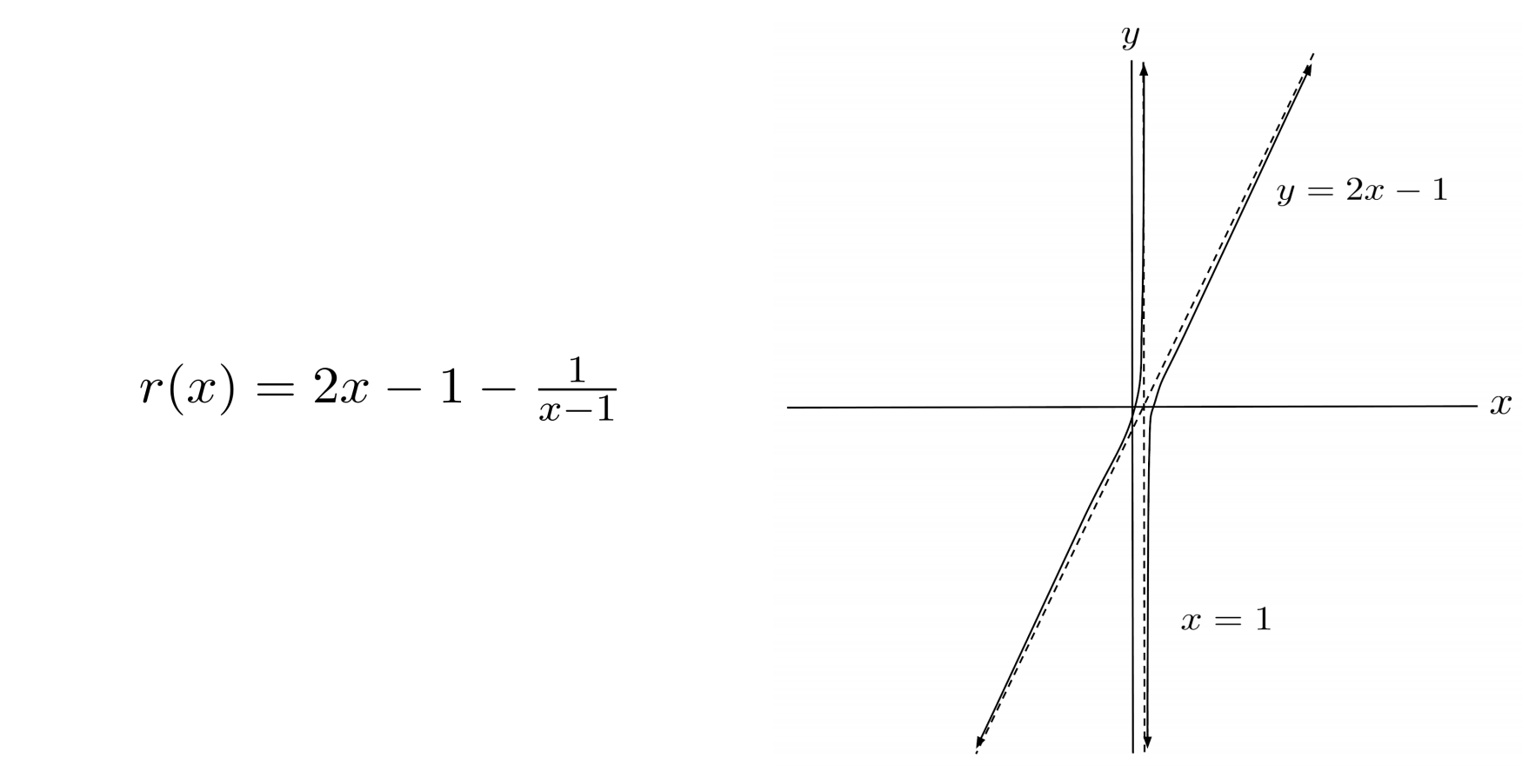
For example, the proper form of $r(x)=\frac{2x^2-3x}{x-1}$ is given by $r(x)=2x-1-\frac{1}{x-1}$, which has $2x-1$ as its whole number term.
As a result, $r$ has a slant asymptote at $y=2x-1$, which appears in the graph of $r$ below.
Existence and Degree
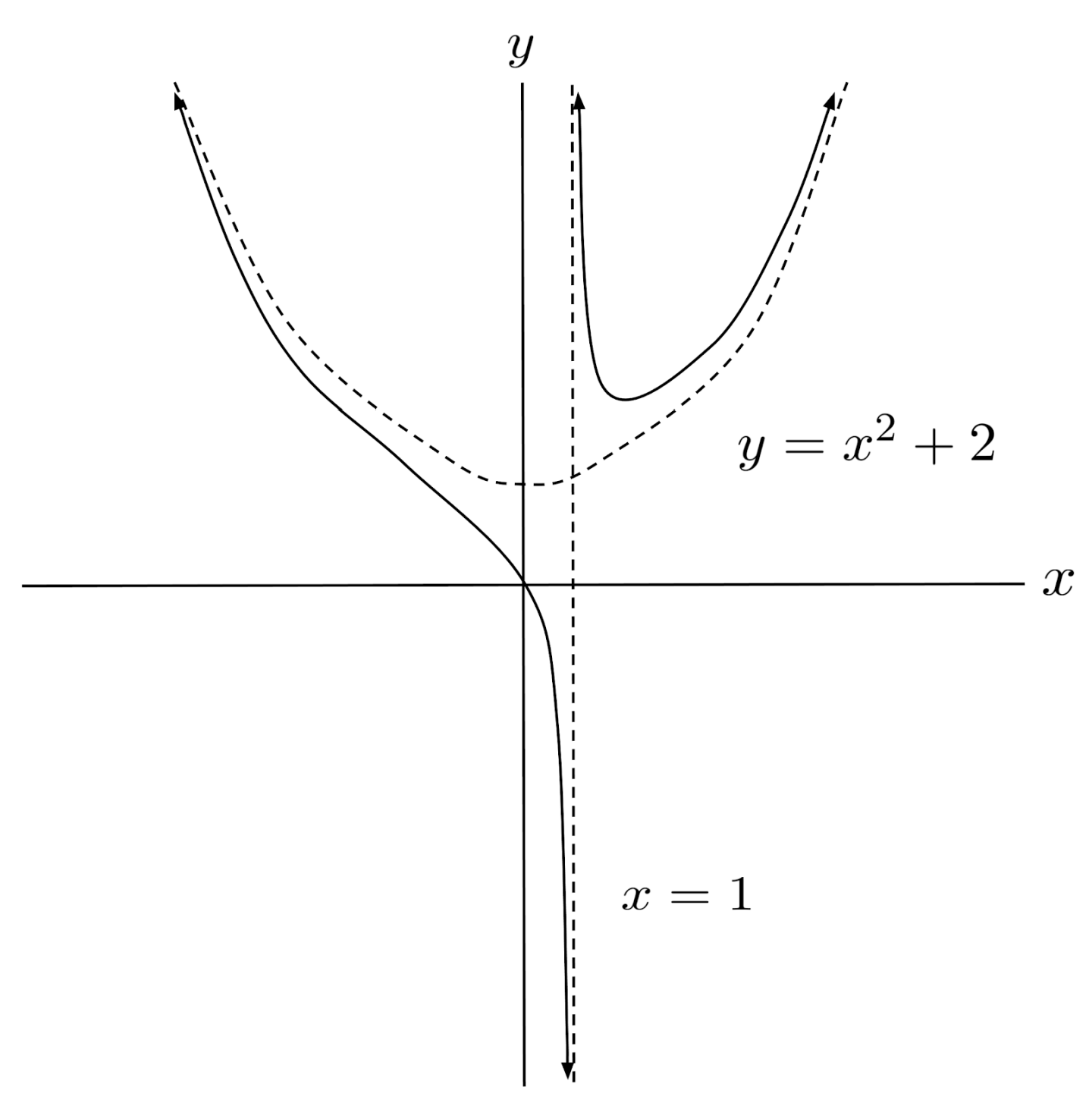
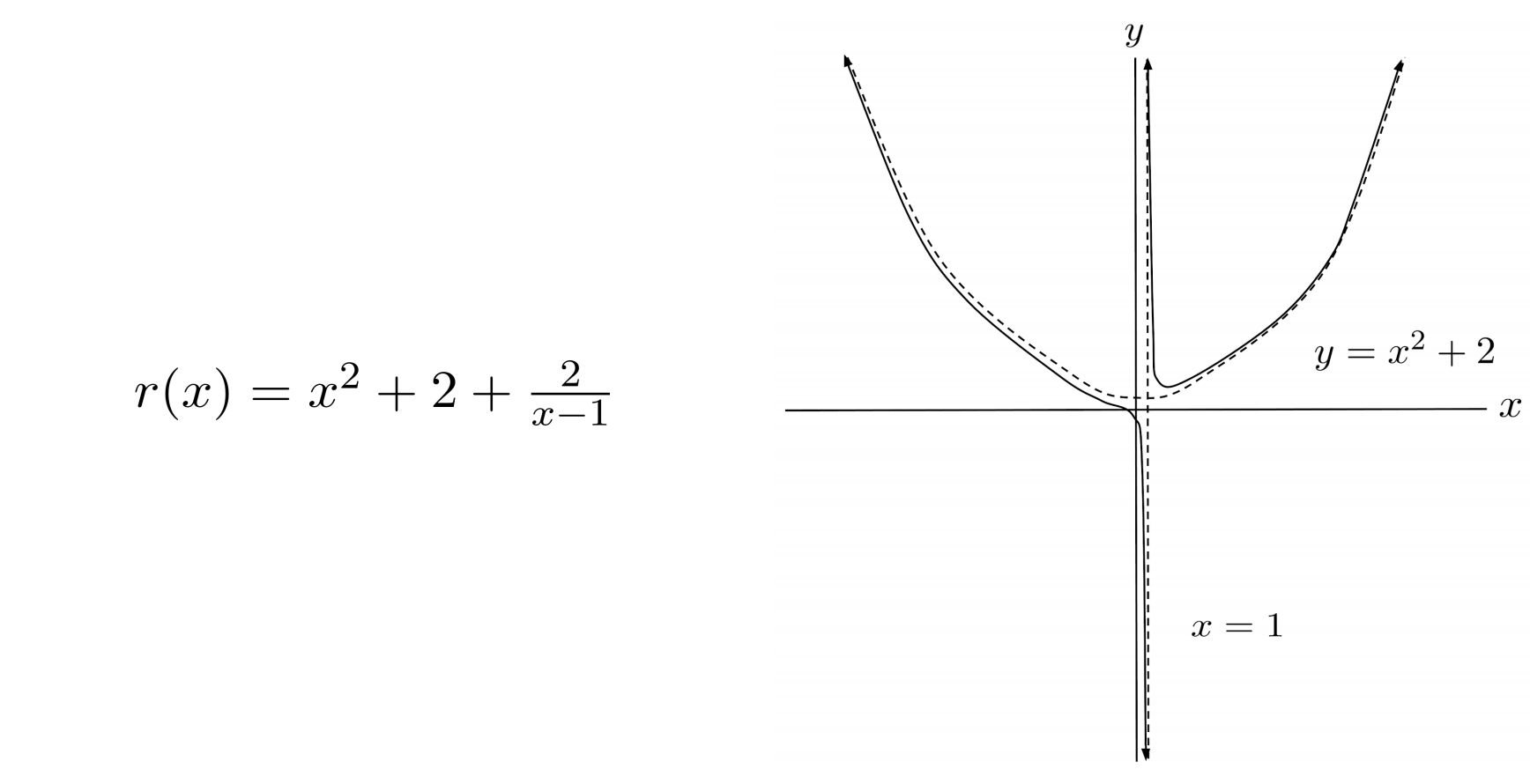
In general, the whole number part of the proper form is an asymptote. If the whole number part is of a higher degree, say $r(x)=\frac{x^3-x^2+2x}{x-1}$ with proper form $r(x)=x^2+2+\frac{2}{x-1}$, then $r$ has a polynomial asymptote at $y=x^2+2$.
The graph of $r$ approaches this asymptote just like it would approach any other horizontal or slant asymptote.
In general, a rational function has a horizontal, slant, or polynomial asymptote if the degree of the denominator is less than the degree of the numerator. The degree of the asymptote is given by the difference in degrees of the numerator and denominator.
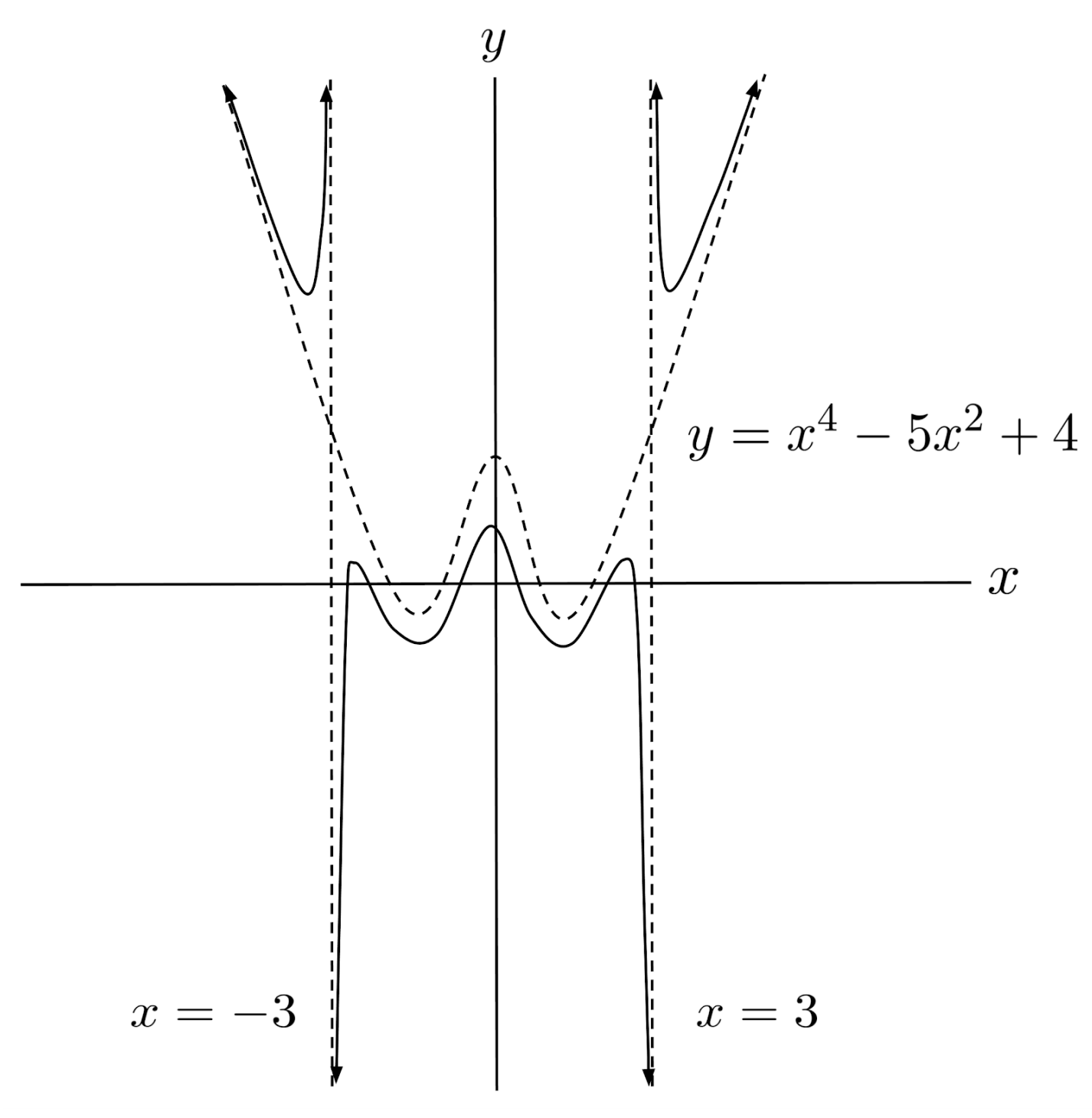
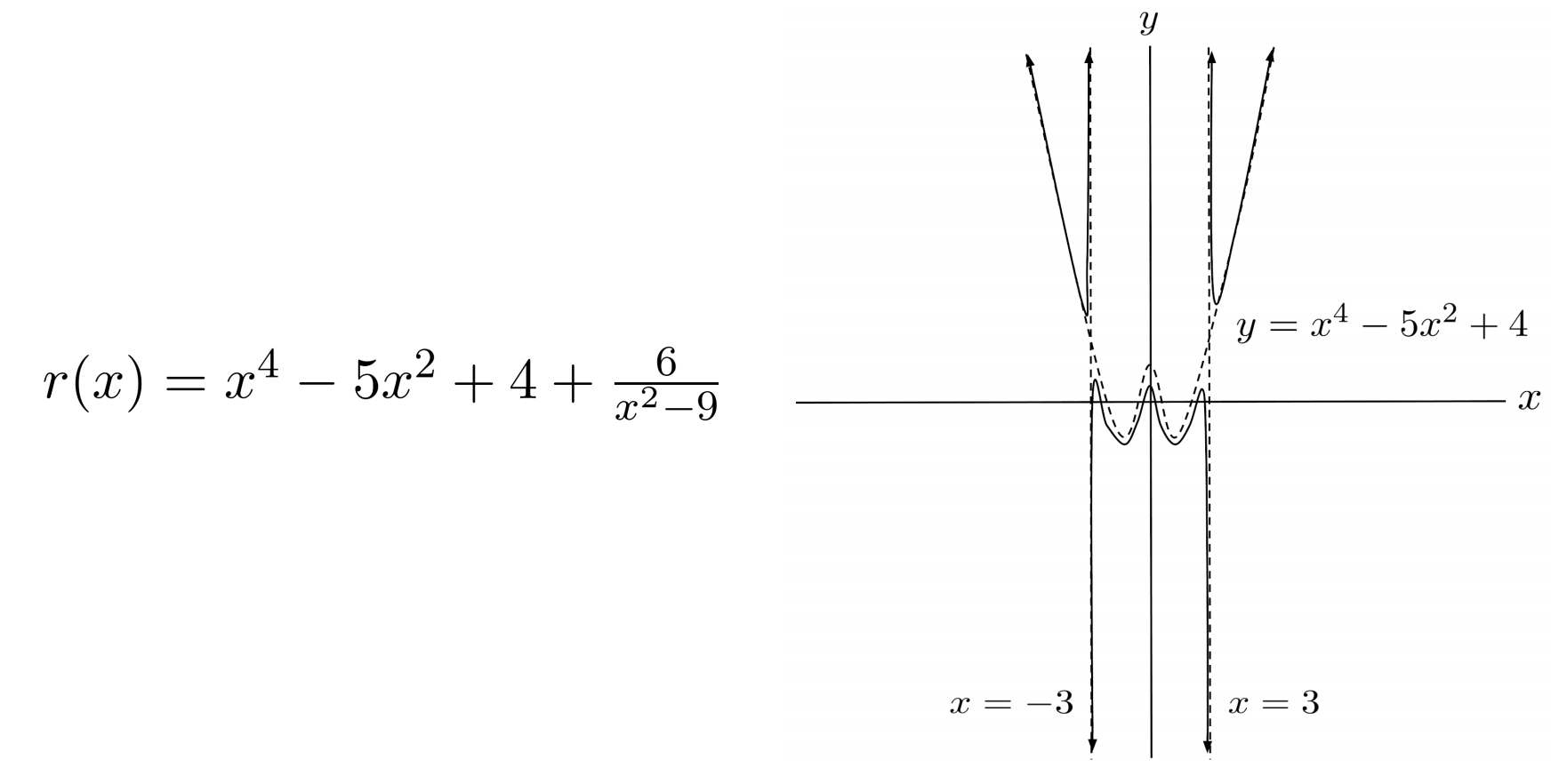
For example, $r(x)=\frac{x^6-14x^4+49x^2-30}{x^2-9}$ has a difference in degrees of $6-2=4$, so we should expect an asymptote of degree $4$. Indeed, the proper form of the function is $r(x)=x^4-5x^2+4+\frac{6}{x^2-9}$ which indicates a polynomial asymptote of $y=x^4-5x^2+4$.
Big Picture
Zooming out of the previous graphs, we can see the big picture of rational functions: they look like their whole number part (i.e. their polynomial asymptotes), except at the singularities (vertical asymptotes), when the denominator of the fractional part becomes extremely small and the fraction blows up to positive or negative infinity.
Exercises
Use vertical and horizontal/slant/polynomial asymptotes to graph the following rational functions. (You can view the solution by clicking on the problem.)
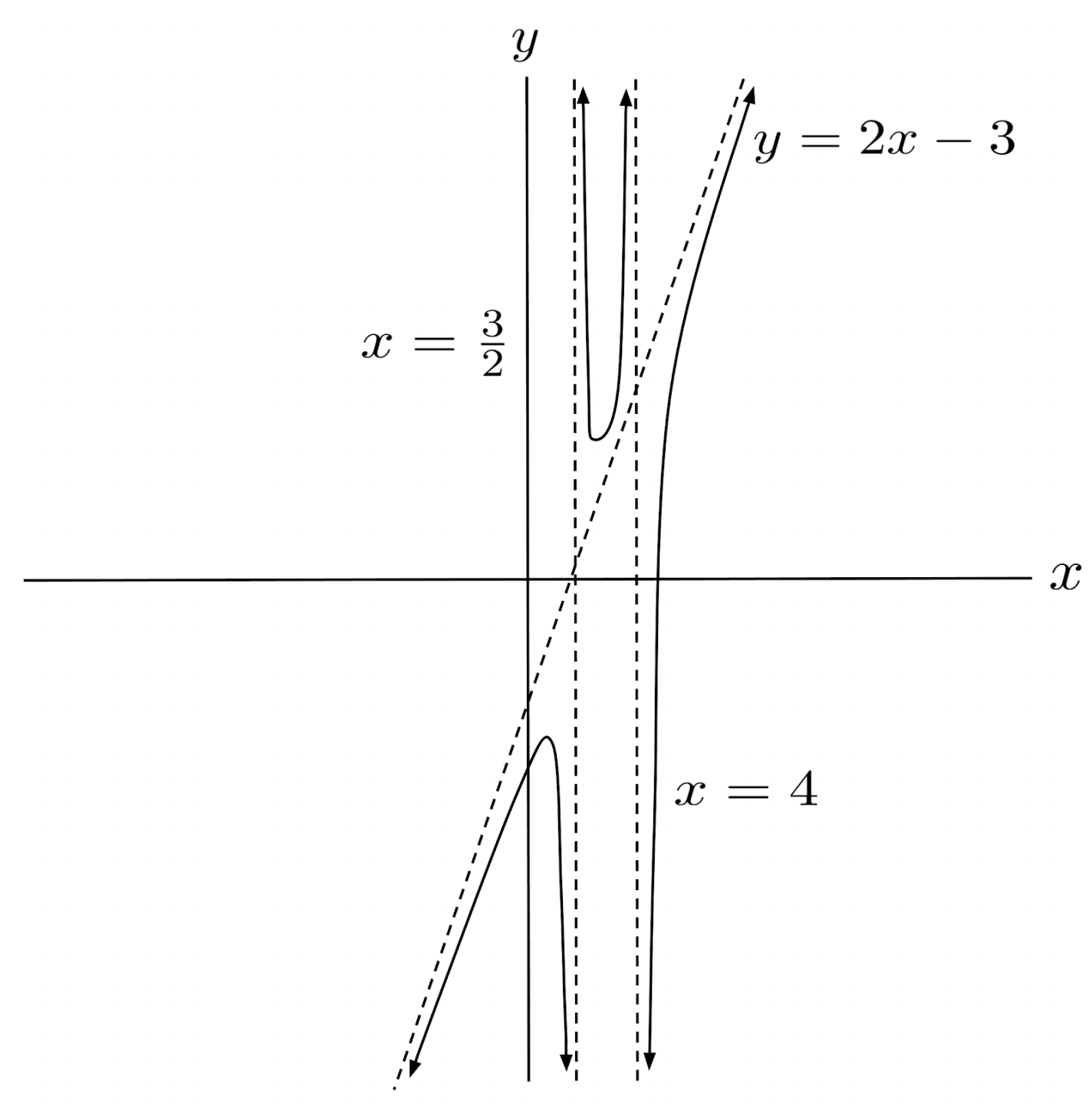
$1) \hspace{.5cm} r(x)=\dfrac{4x^3-28x^2+56x-35}{2x^2-11x+12}$
Solution:
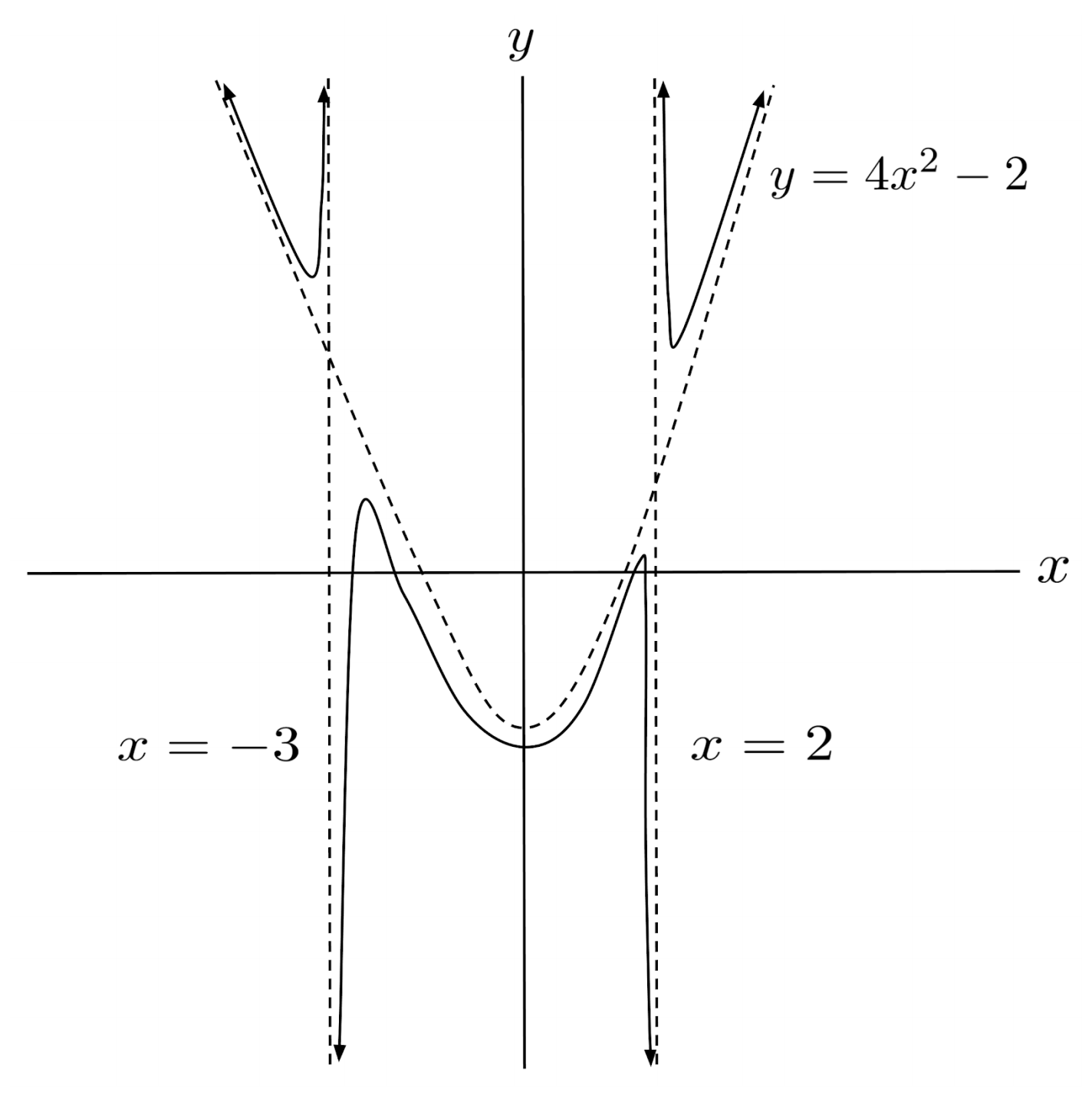
$2) \hspace{.5cm} r(x)=\dfrac{4x^4+4x^3-26x^2-2x+13}{x^2+x-6}$
Solution:
$3) \hspace{.5cm} r(x)=\dfrac{-x^4+10x^3+100}{x^3-5x^2-4x+20}$
Solution:
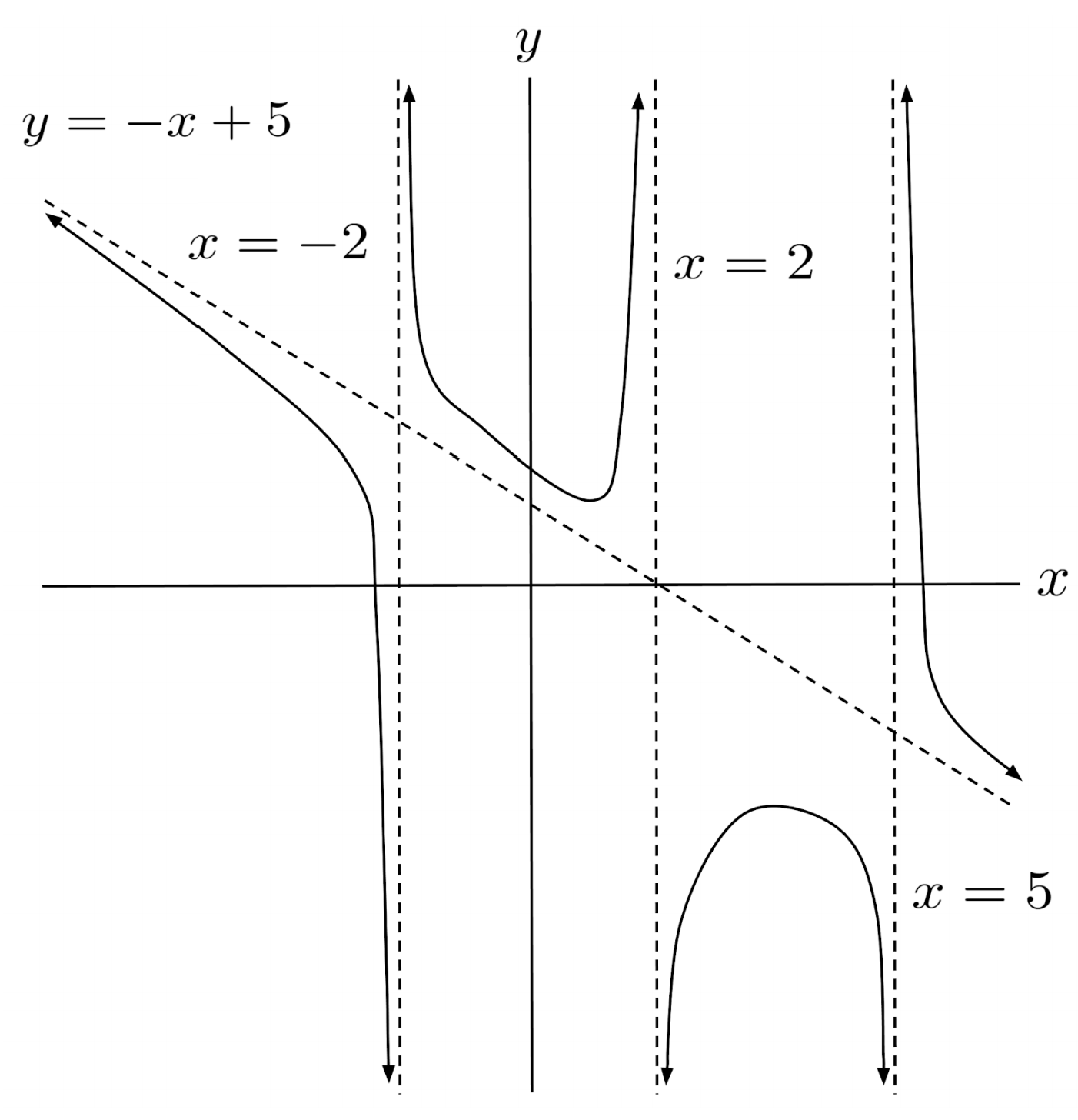
$4) \hspace{.5cm} r(x)=\dfrac{-2x^4+5x^3+14x^2-30}{2x^2-3x-5}$
Solution:
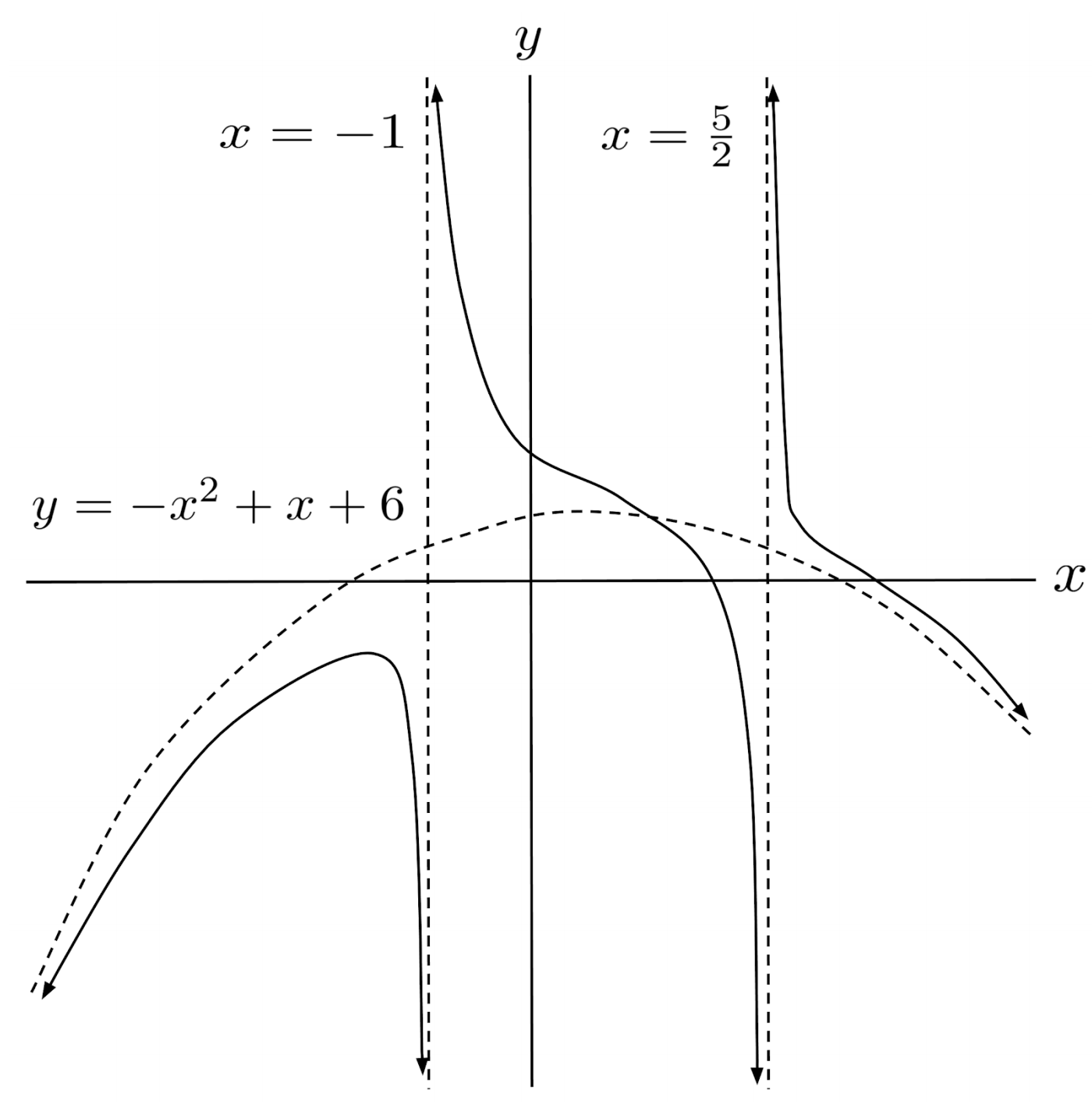
$5) \hspace{.5cm} r(x)=\dfrac{-x^6+7x^4+11x^3+5}{x^3-7x-6}$
Solution:
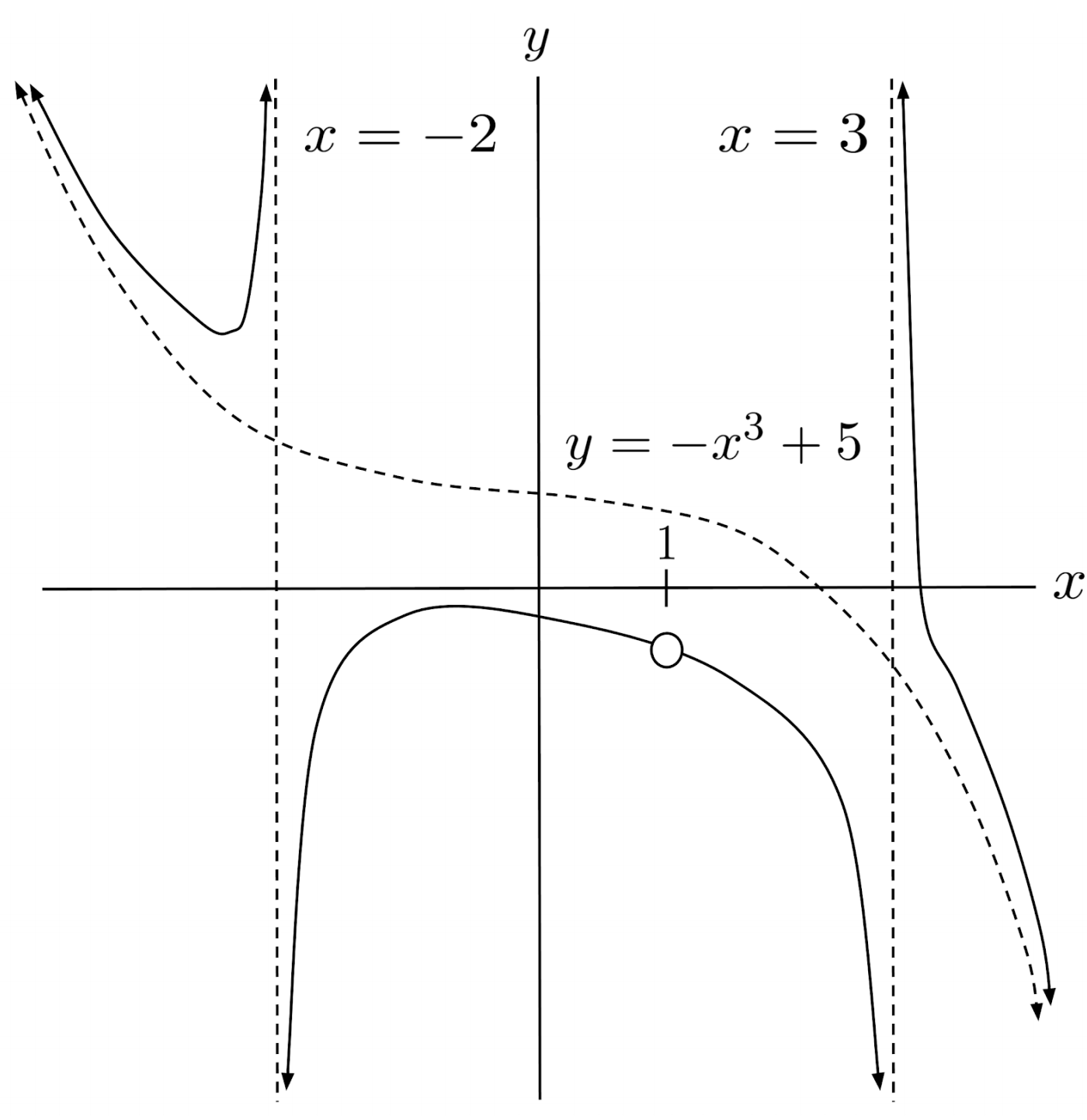
$6) \hspace{.5cm} r(x)=\dfrac{-6x^6-7x^5+80x^4+70x^3-254x^2}{6x^2+7x-20}$
Solution:
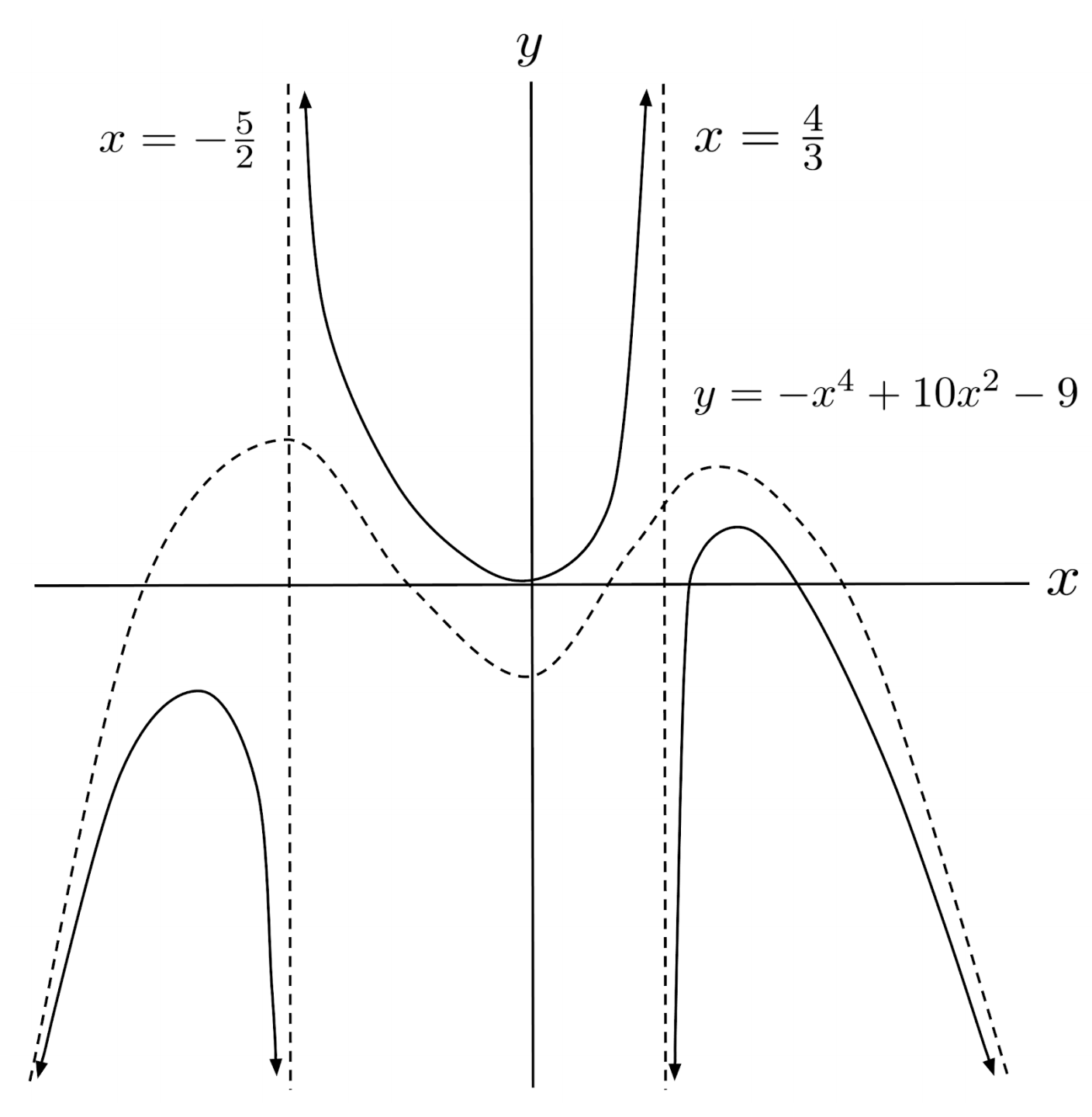
This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Graphing Rational Functions with Slant and Polynomial Asymptotes. In Justin Math: Algebra. https://justinmath.com/graphing-rational-functions-with-slant-and-polynomial-asymptotes/