Graphing Calculator Drawing: Slanted Lines

by Justin Skycak (@justinskycak) on

Slanted lines can be used to draw a spider web.

This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Slanted Lines. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-slanted-lines/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Setup. Navigate to https://www.desmos.com/calculator. Be sure to sign in so that you can save your graph.

Demonstration - Slope. Observe the graph as you type each of the following inputs. In general, the line $y=mx$ goes $m$ units up per unit it goes right.

$\begin{align*} y&=10x \\[10pt] y&=1x \\[10pt] y&=0.1x \\[10pt] y&=0x \\[10pt] y&=-0.1x \\[10pt] y&=-1x \\[10pt] y&=-10x \end{align*}$


Demonstration - Intercept. Observe the graph as you type each of the following inputs. In general, the graph $y=mx+b$ crosses the y-axis at the point $(0,b).$

$\begin{align*} y&=x+5 \\[10pt] y&=x+2 \\[10pt] y&=x+1 \\[10pt] y&=x+0 \\[10pt] y&=x-1 \\[10pt] y&=x-2 \\[10pt] y&=x-5 \end{align*}$


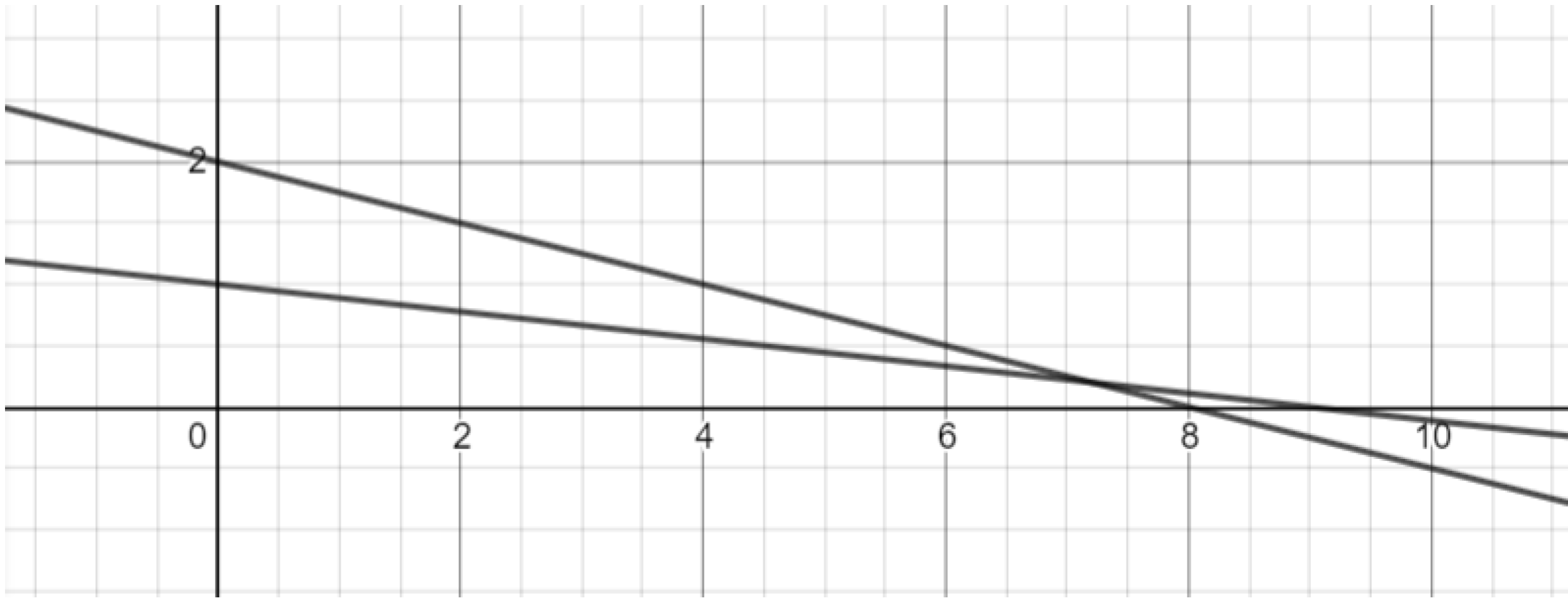
Exercise. Draw the two lines shown below. (Hint: one of the lines is given by $y=1-\frac{1}{9}x.$)

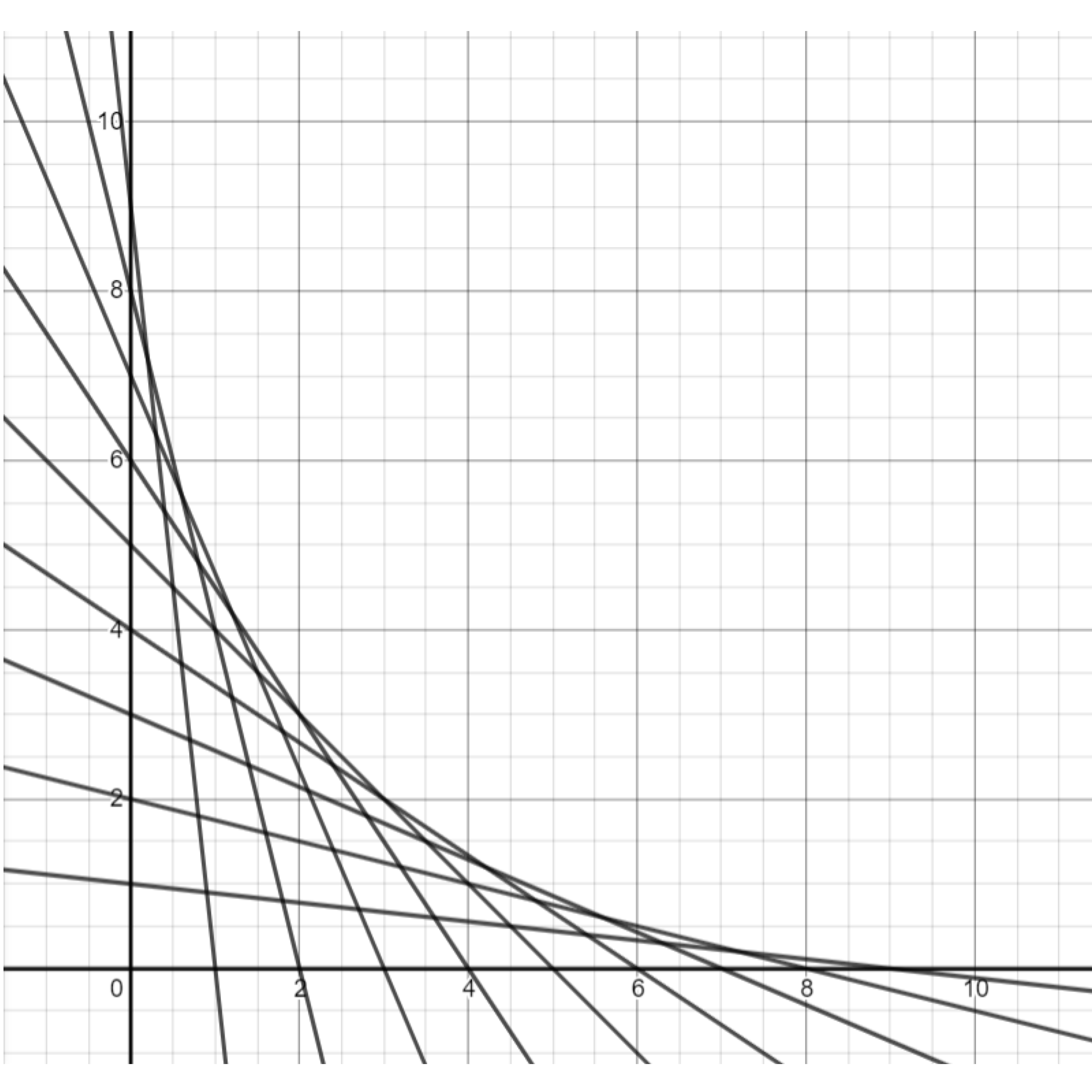
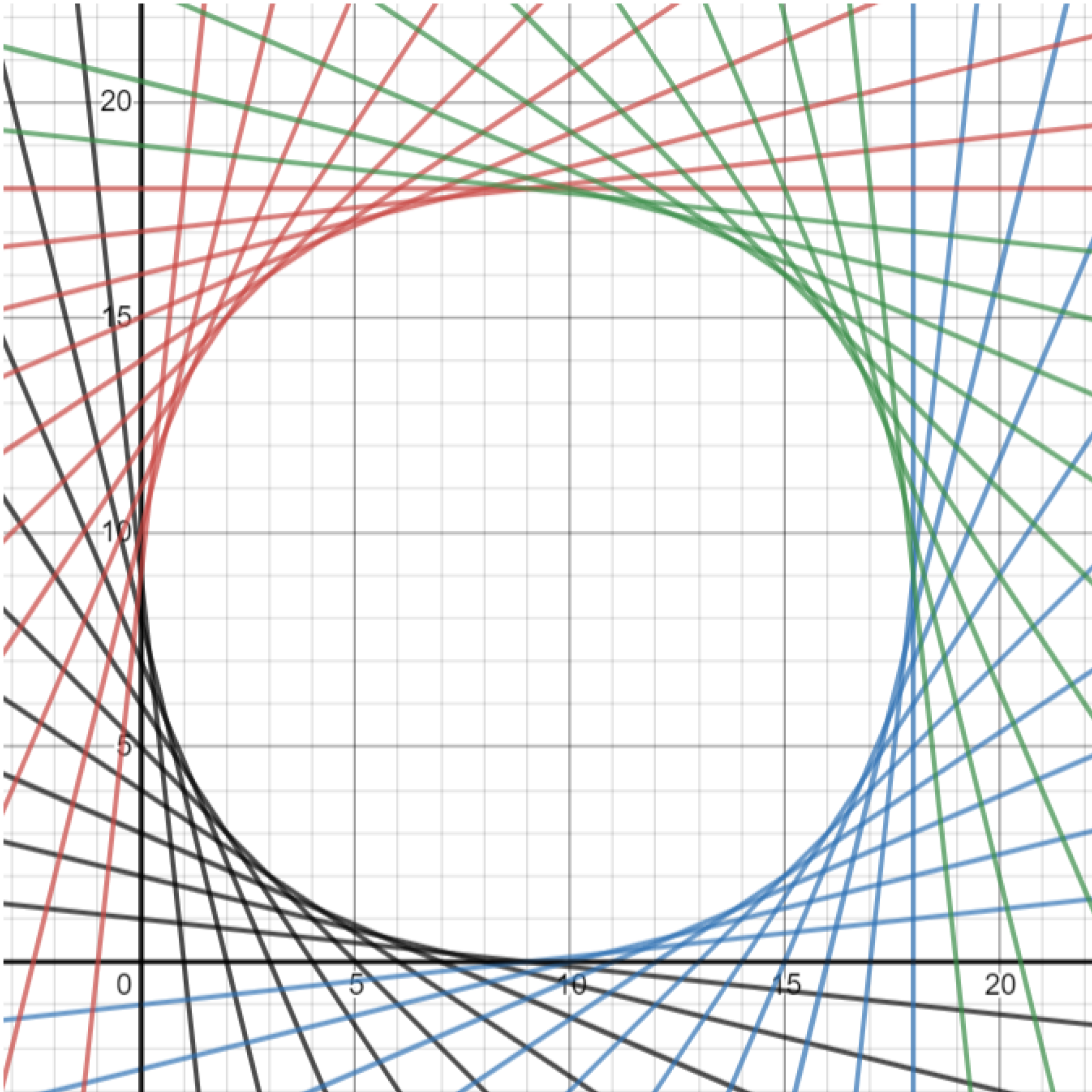
image


Exercise. Draw more lines to reproduce the “spider web” graph shown below.

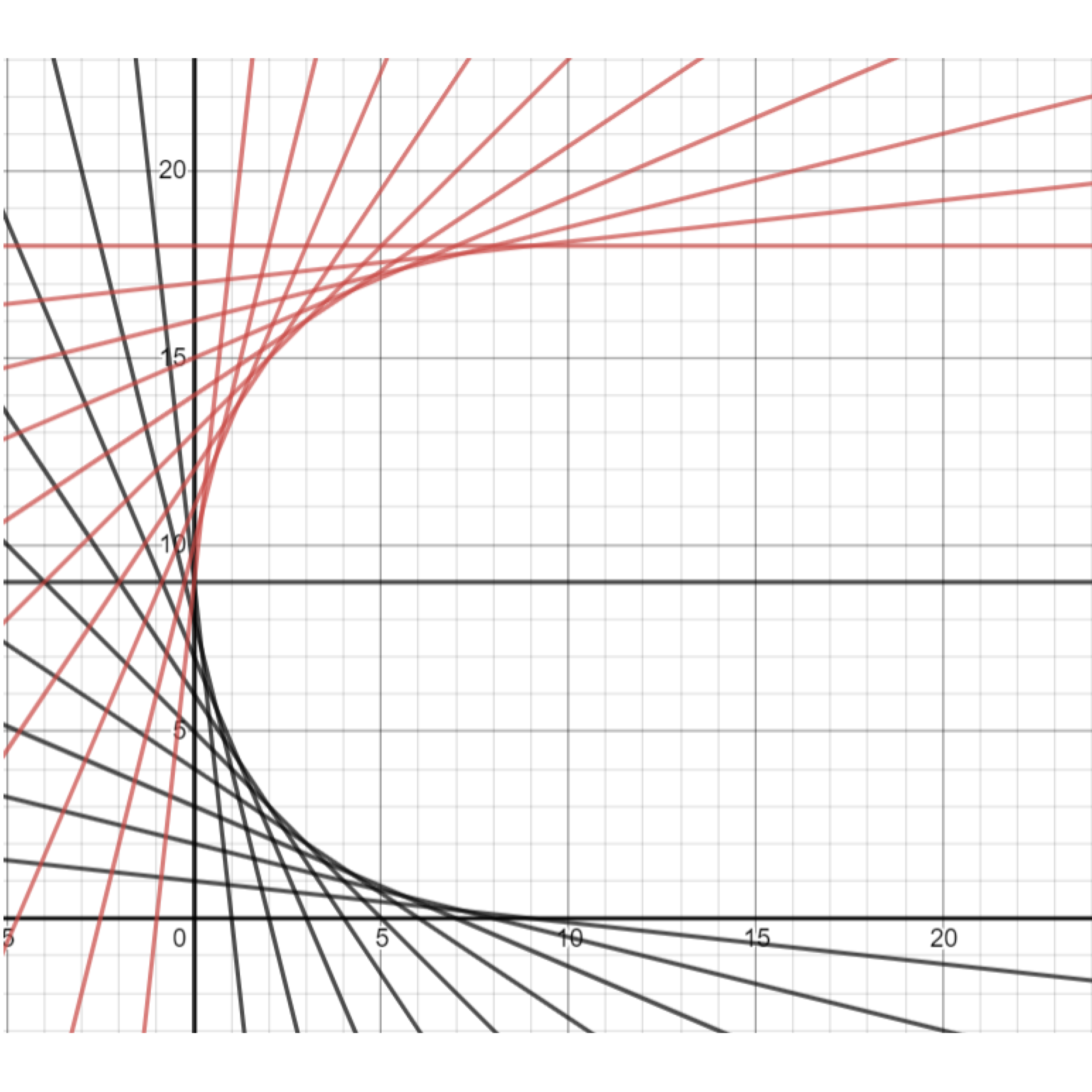
image


Exercise. Draw more lines to reflect the spider web upwards. (Hint: starting with the lines you drew previously, you can make the slopes positive, and adjust the intercepts as needed.)

image


Demonstration. The equation $y=m(x-a)+b$ creates a line with slope $m$ through the point $(a,b).$

  • The line through $(9,0)$ with slope $\frac{1}{9}$ is given by $y=\frac{1}{9}(x-9)+0.$
  • The line through $(10,0)$ with slope $\frac{2}{8}$ is given by $y=\frac{2}{8}(x-9)+0.$


Exercise. Draw more lines to complete the bottom-right portion of your spider web. Two of the lines are given in the previous demonstration.

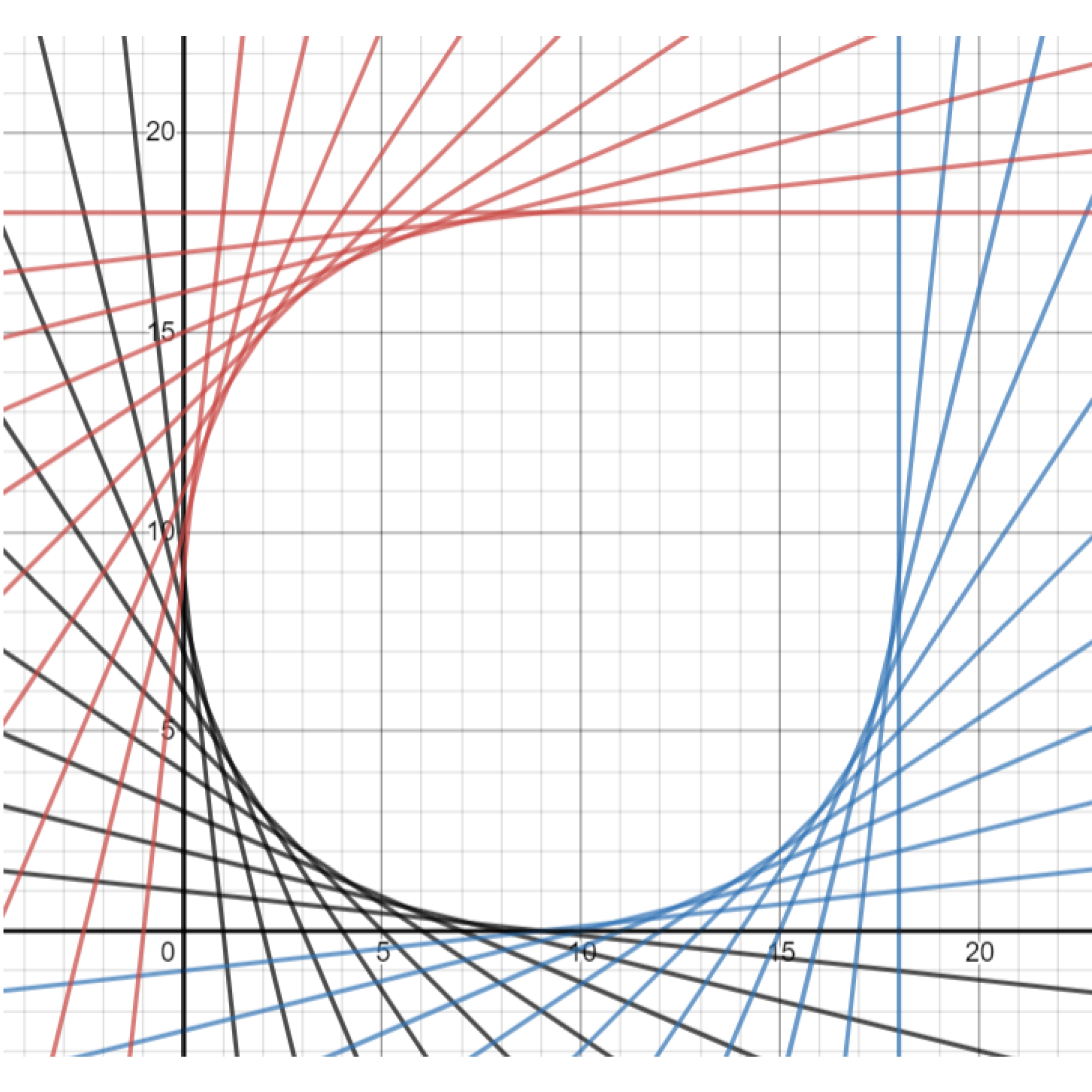
image


Exercise. Using the equation $y=m(x-a)+b,$ complete the top-right corner of your spider web. Two lines are provided below.

  • The line through $(18,17)$ with slope $-\frac{1}{9}$ is given by $y=-\frac{1}{9}(x-18)+17.$
  • The line through $(18,16)$ with slope $-\frac{2}{8}$ is given by $y=-\frac{2}{8}(x-18)+16.$


image


This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Slanted Lines. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-slanted-lines/


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.