Graphing Calculator Drawing: Shading with Sine

by Justin Skycak (@justinskycak) on

High-frequency sine waves can be used to draw shaded regions.

This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Shading with Sine. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-shading-with-sine/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Setup. Navigate to https://www.desmos.com/calculator. Be sure to sign in so that you can save your graph.

Demonstration - High Frequency. Observe the graph as you type each of the following inputs. In general, the graph of $y=\sin(vx)$ looks more and more solid as $v$ increases.

$\begin{align*} y&=\sin(x) \\[10pt] y&=\sin(10x) \\[10pt] y&=\sin(100x) \\[10pt] y&=\sin(1000x) \end{align*}$


Demonstration - Thickening a Curve. Observe the graph as you type each of the following inputs. In general, for large $v,$ the graph of $y=f(x)+A\sin(vx)$ thickens the curve $y=f(x)$ to have a vertical thickness of $2A.$

$\begin{align*} y&=x+0.1\sin(1000x) \\[10pt] y&=x^2+0.1\sin(1000x) \\[10pt] y&=x^2+0.5\sin(1000x) \\[10pt] y&=\sin(x)+0.1\sin(1000x) \\[10pt] y&=\sin(x)+0.5\sin(1000x) \end{align*}$


Demonstration - Varying Amplitude. Observe the graph as you type each of the following inputs. In general, when $v$ is large, the graph of $y=f(x)\sin(vx)$ shades the area between the graphs of $y=-f(x)$ and $y=f(x).$

$\begin{align*} y&=x\sin(1000x) \\[10pt] y&=x^2\sin(1000x) \\[10pt] y&=\left( \sin x \right) \sin (1000x) \end{align*}$


Demonstration - Shifts. Observe the graph as you type each of the following inputs. In general, the graph of $y=f(x-a)\sin(vx)+b$ is the graph of $y=f(x)\sin(vx)$ shifted right by $a$ units and up by $b$ units.

$\begin{align*} y&=x^2 \sin(1000x) \\[10pt] y&=(x-2)\sin(1000x)+5 \end{align*}$


Demonstration - Limitations. Observe the graph as you type each of the following inputs.

$\begin{align*} y&=\sin(1000x) \lbrace 5 < x < 10 \rbrace \\[10pt] y&=(x-2)^2 \sin(1000x) \lbrace 2 < x < 4 \rbrace \\[10pt] y&=\left(\sqrt{x-3}\right)\sin(1000x)+5\left\{3<x<4\right\} \end{align*}$


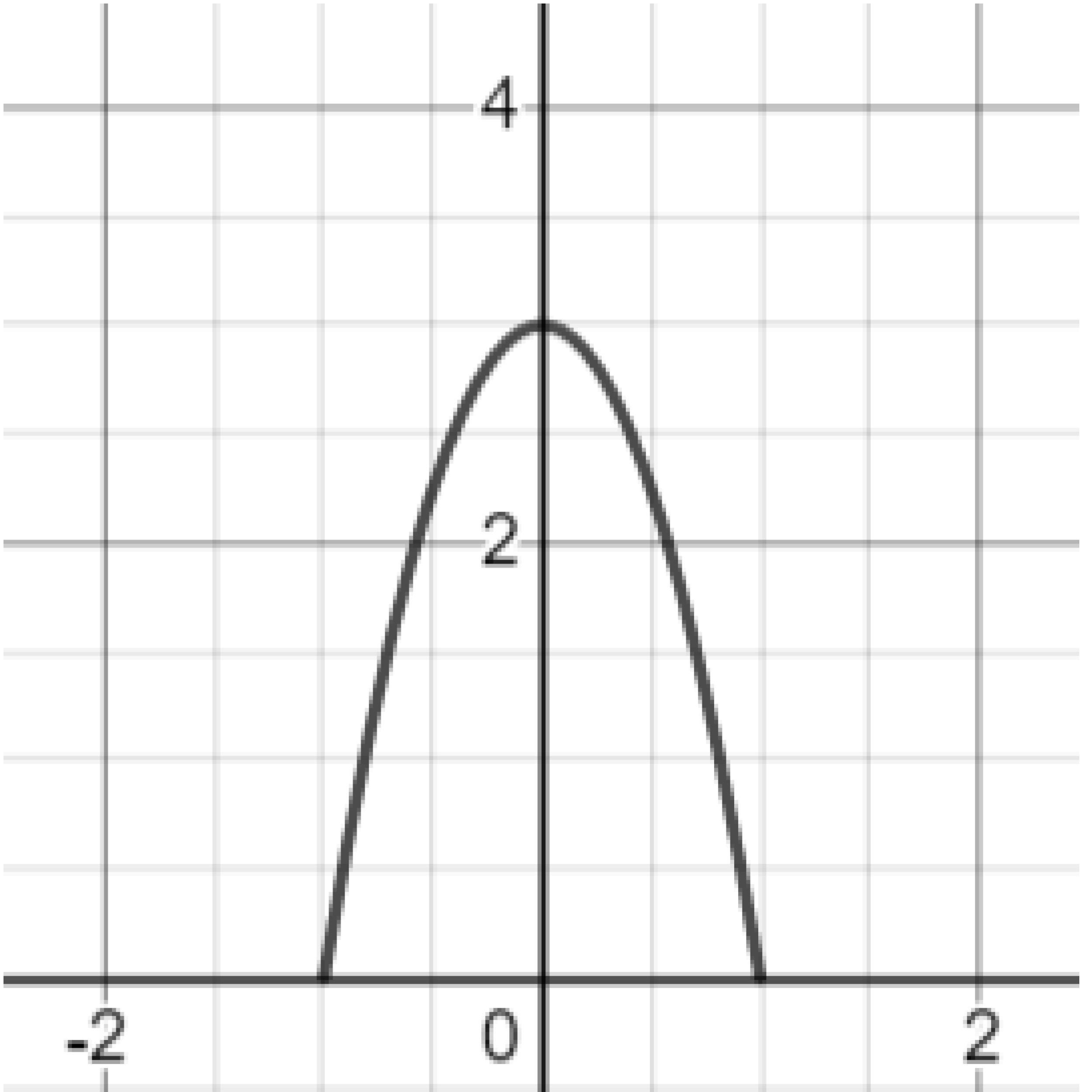
Exercise. Reproduce the downward parabola shown below.

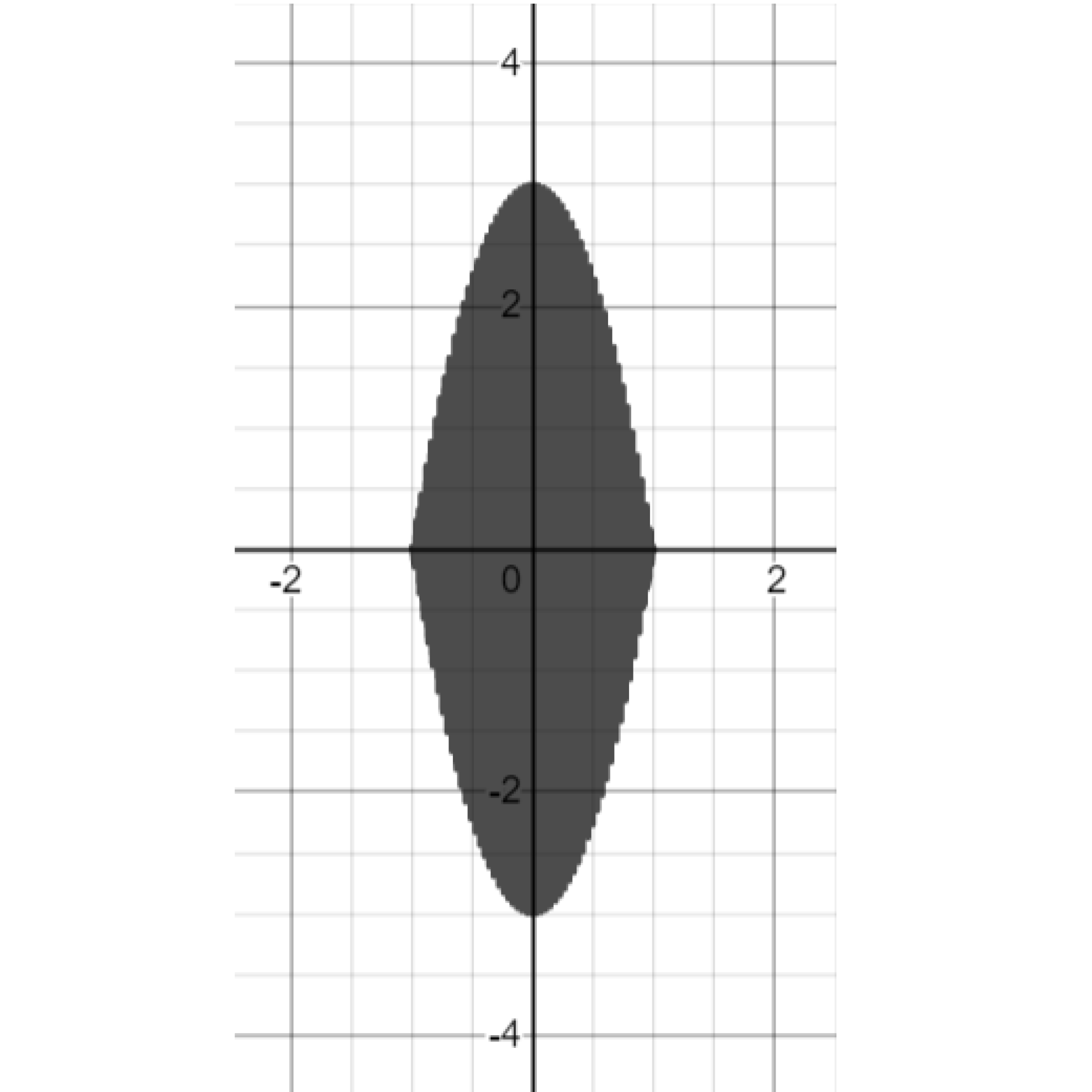
image


Exercise. Use the parabola as the amplitude of a high-frequency sine function to create a shaded area.

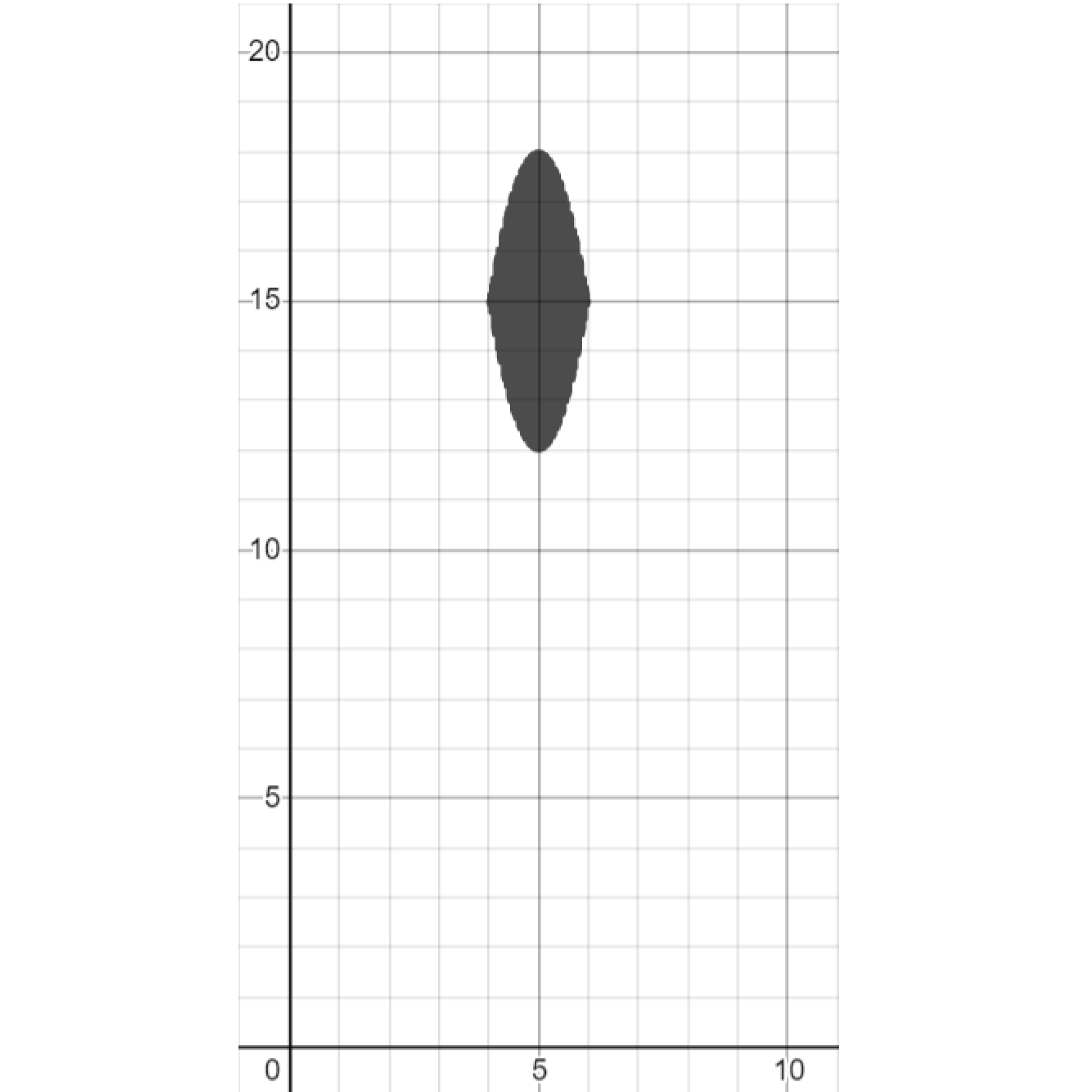
image


Exercise. Shift the shaded area up and right.

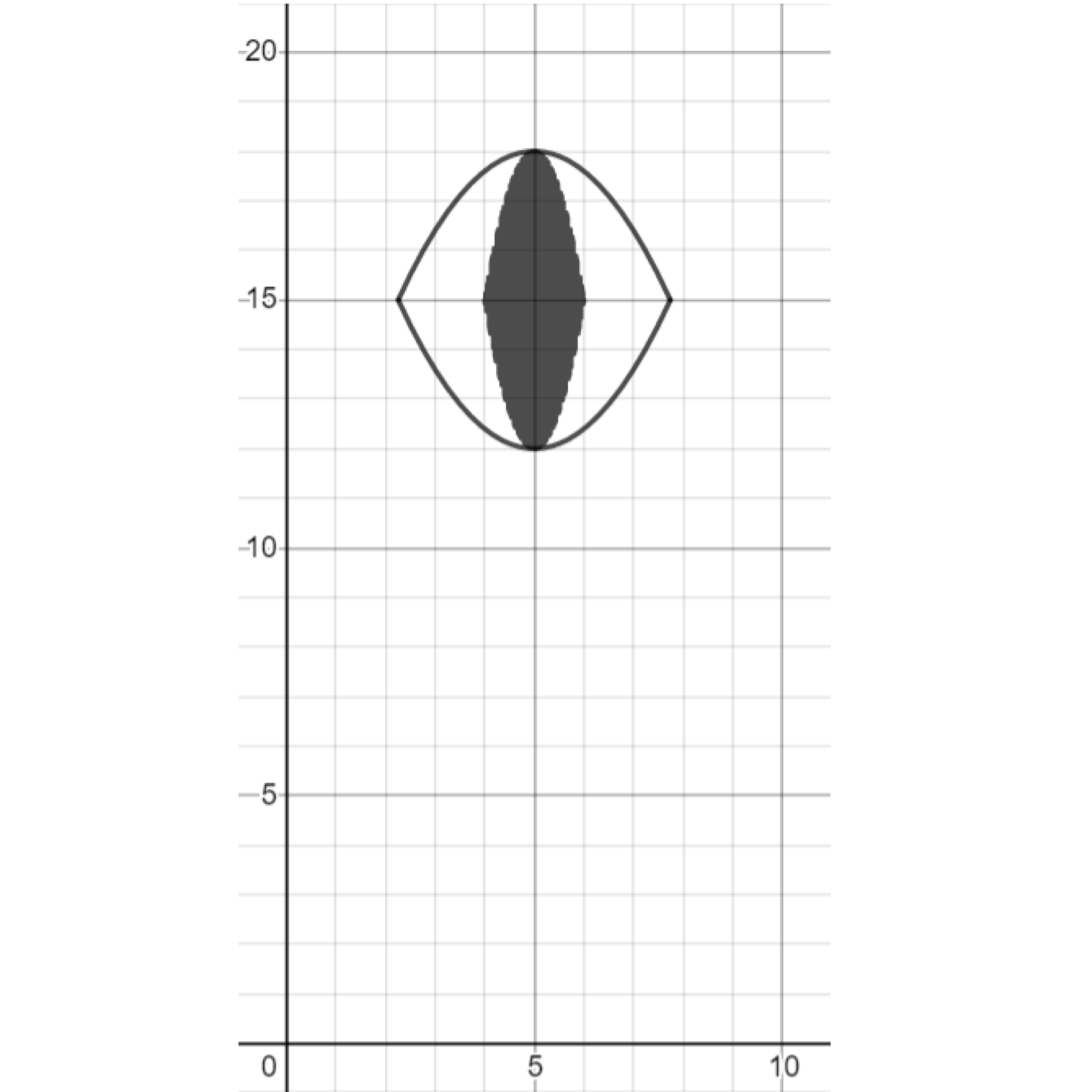
image


Exercise. Draw parabolas around the shaded area to create an eye.

image


Exercise. Create another eye.

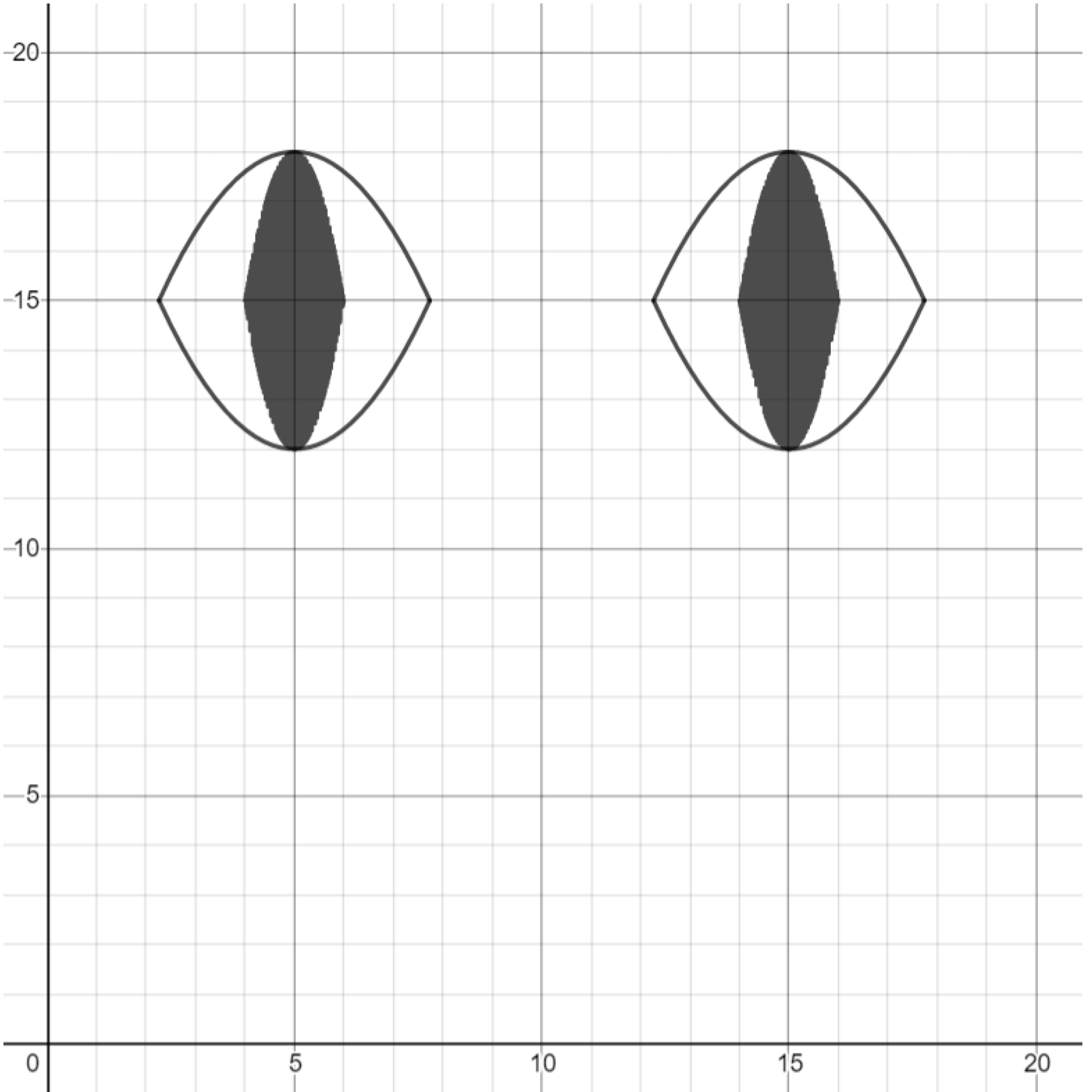
image


Exercise. Create a parabola in the shape of a mouth.

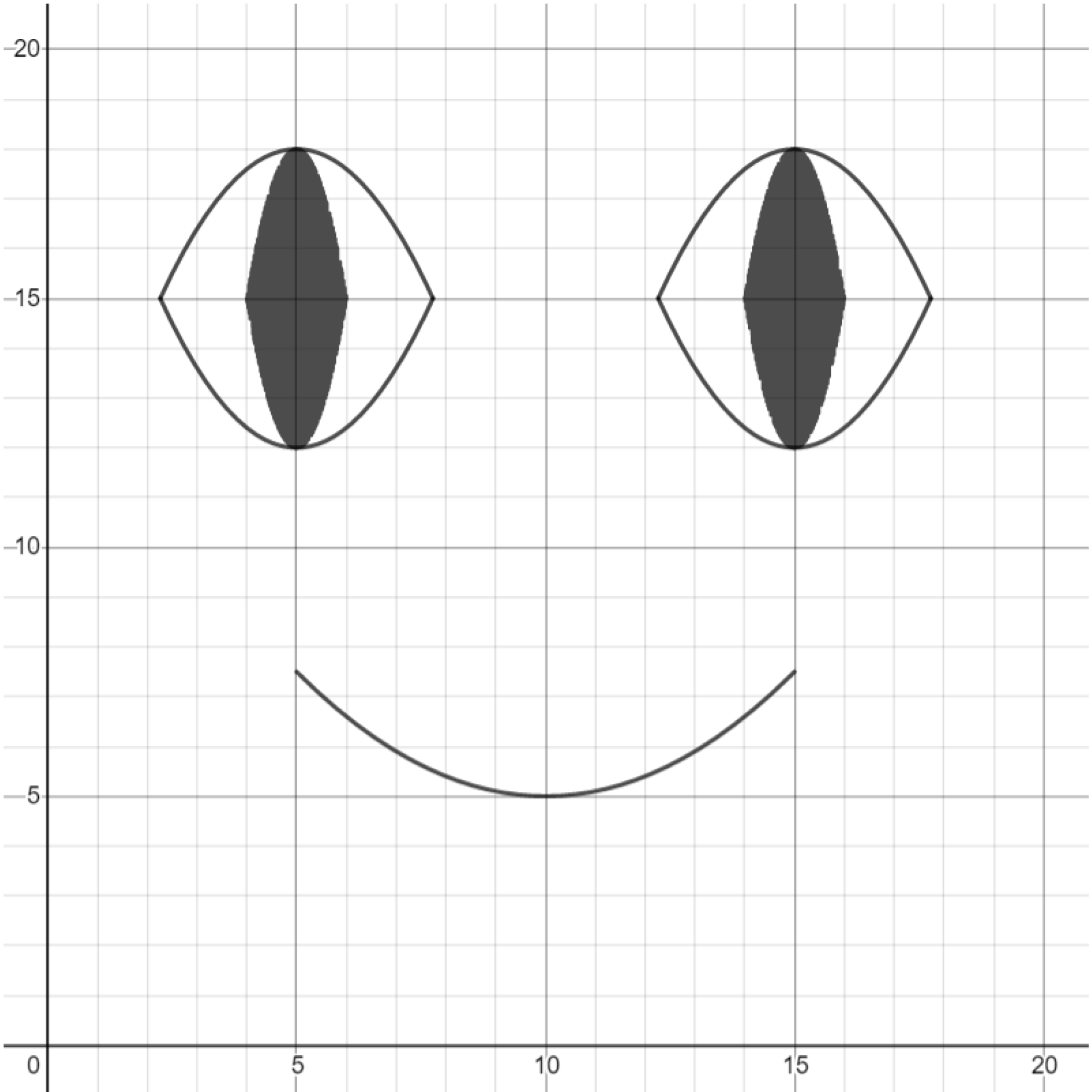
image


Exercise. Thicken the parabola that forms the shape of the mouth.

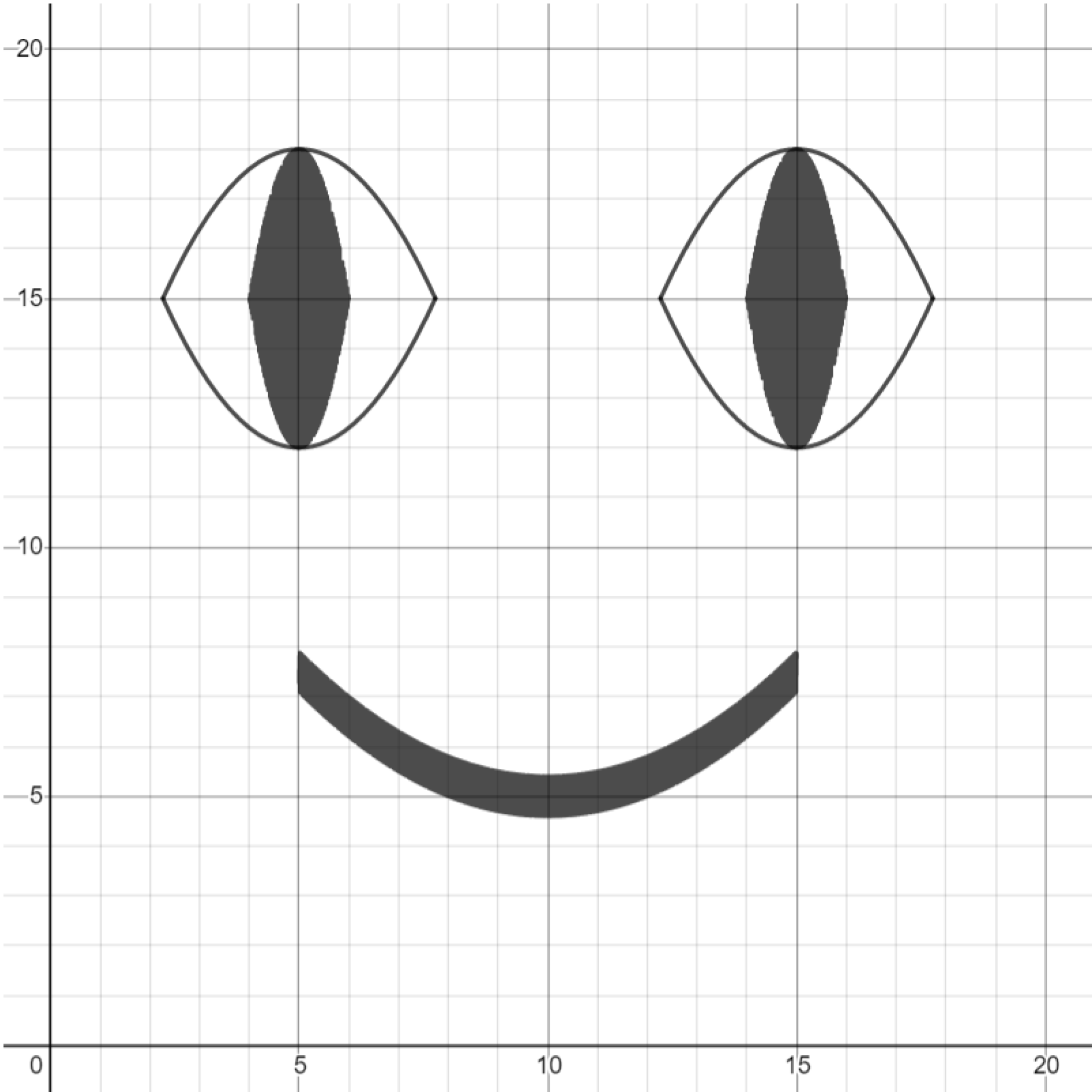
image


Challenge. Make other kinds of emoji faces, such as a sad face or a laughing face.

This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Shading with Sine. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-shading-with-sine/


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.