Graphing Calculator Drawing: Rotation
Absolute value graphs can be rotated to draw stars.
This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Rotation. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-rotation/
Setup. Navigate to https://www.desmos.com/calculator. Be sure to sign in so that you can save your graph.
Demonstration - Rotation. Observe the graph as you type each of the following inputs. In general, a graph can be rotated by an angle of $\theta$ about the origin by replacing $x$ and $y$ with the following expressions:
Note that $\theta$ should be given in radians, and one can convert degrees to radians by multiplying by the conversion factor $\frac{\pi}{180}.$
Exercise. Reproduce the graph below by drawing an absolute value function and then rotating it a fifth of a circle counterclockwise.
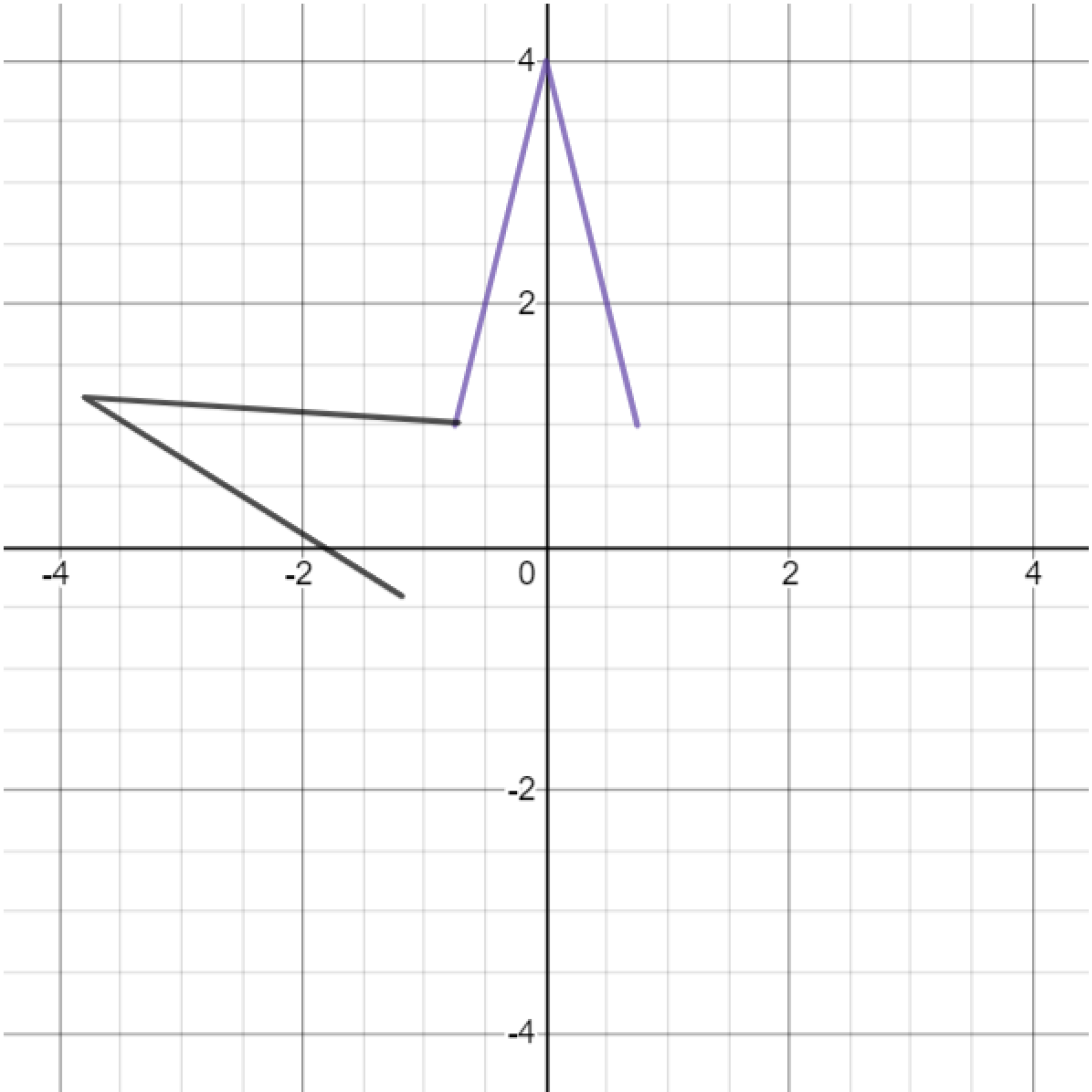
Exercise. Continue drawing rotated absolute value functions to form a star.
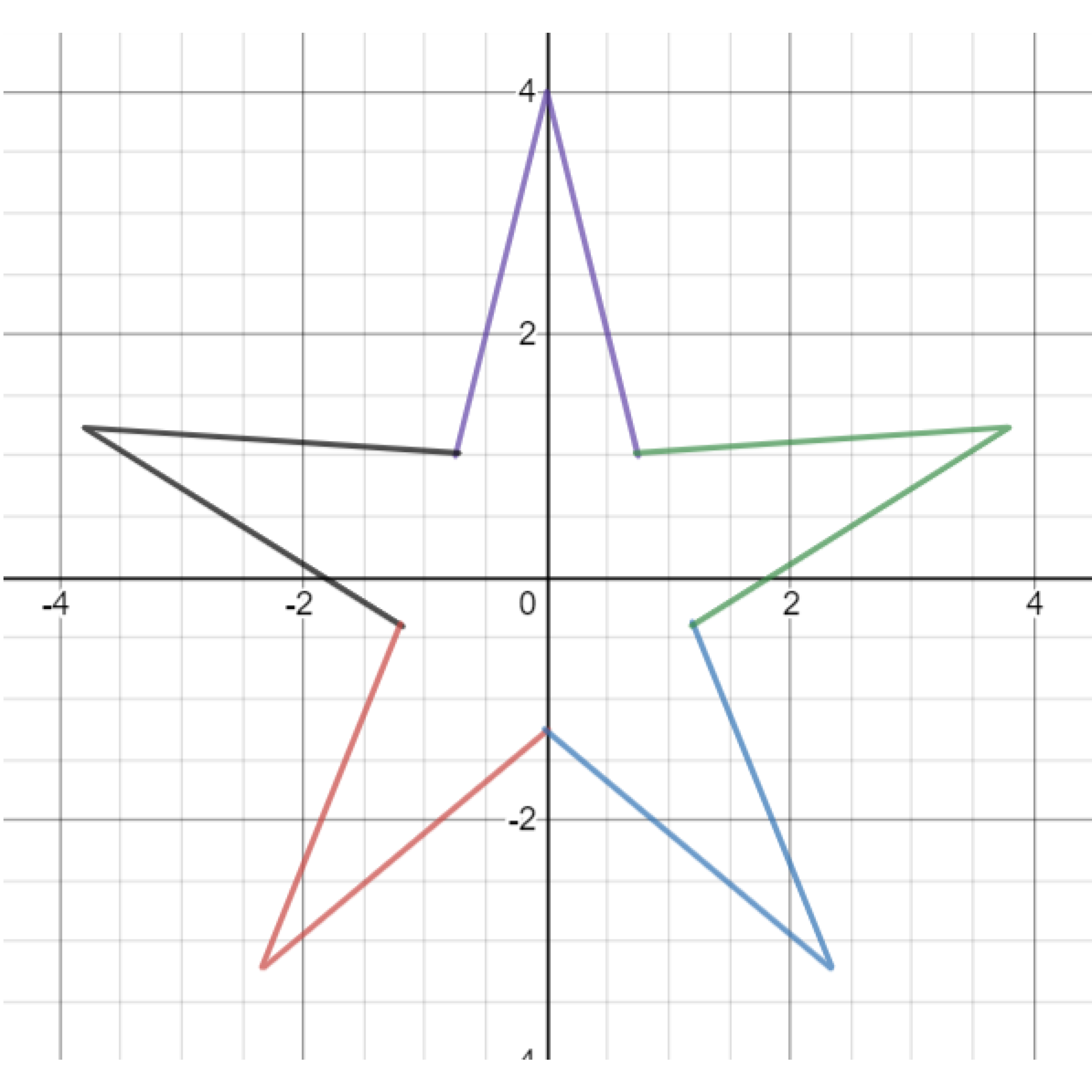
Exercise. Draw a circle that passes through the sharp points of the star.
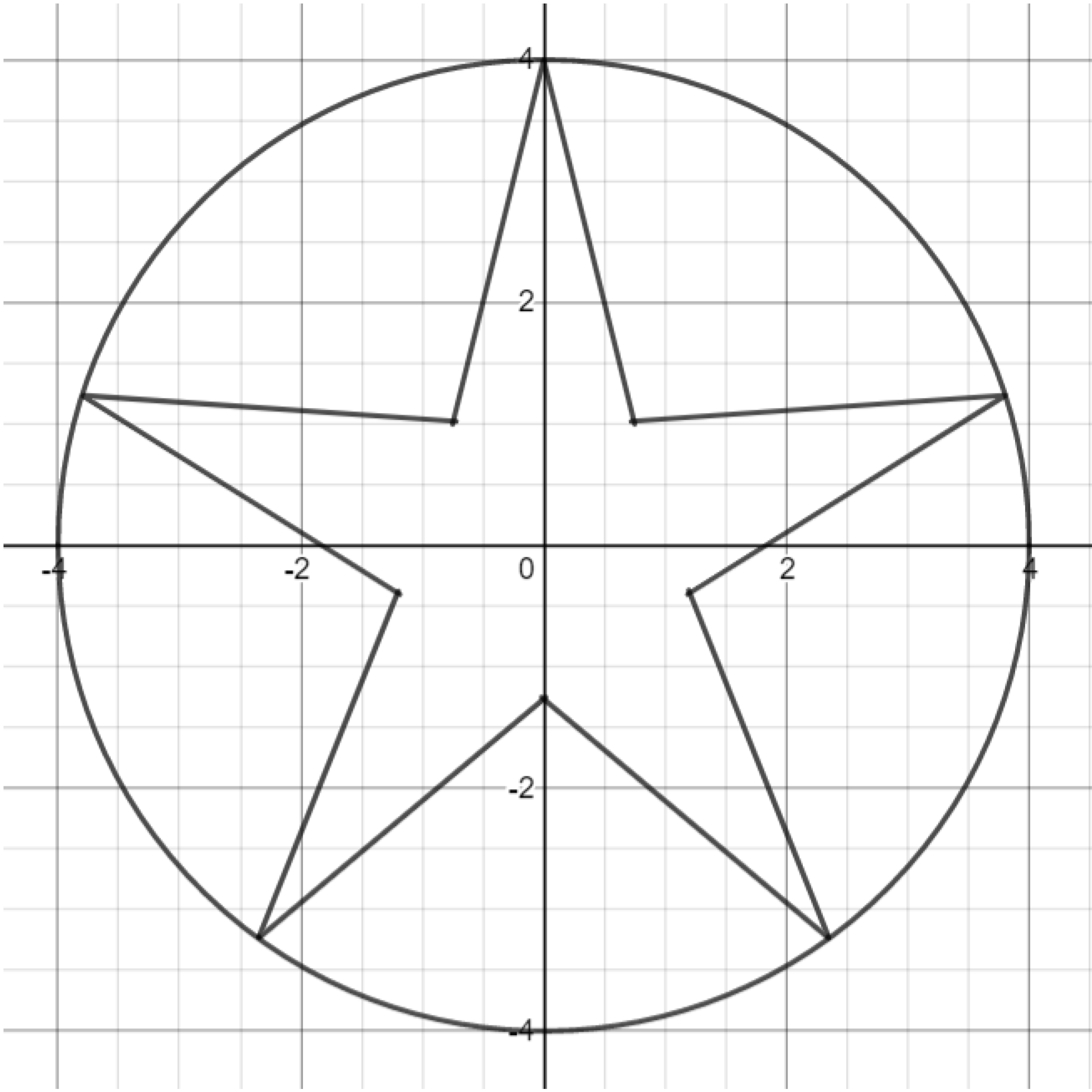
Exercise. Add a background layer by drawing rotated parabolas.
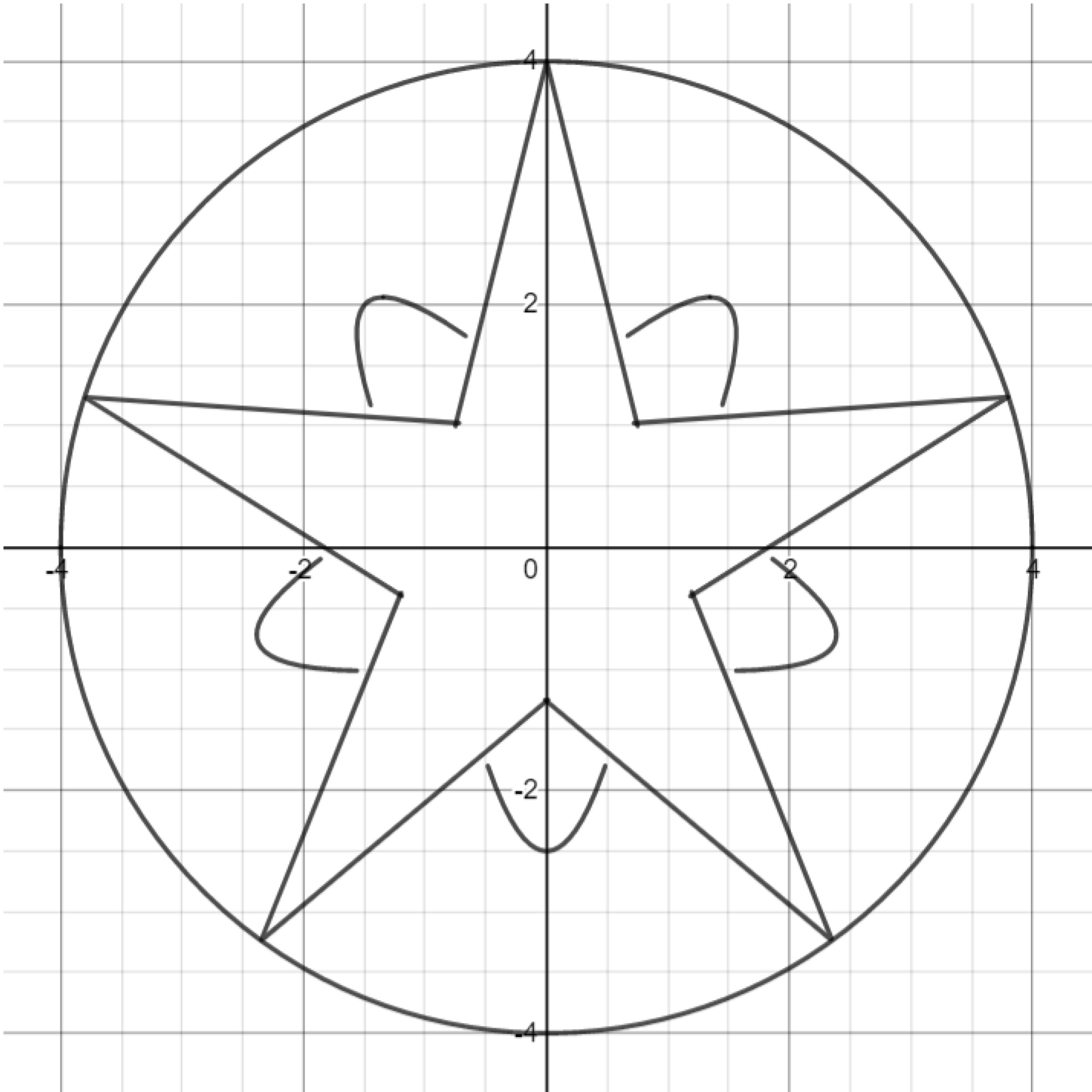
Exercise. Finally, add non-Euclidean ellipses to the background.
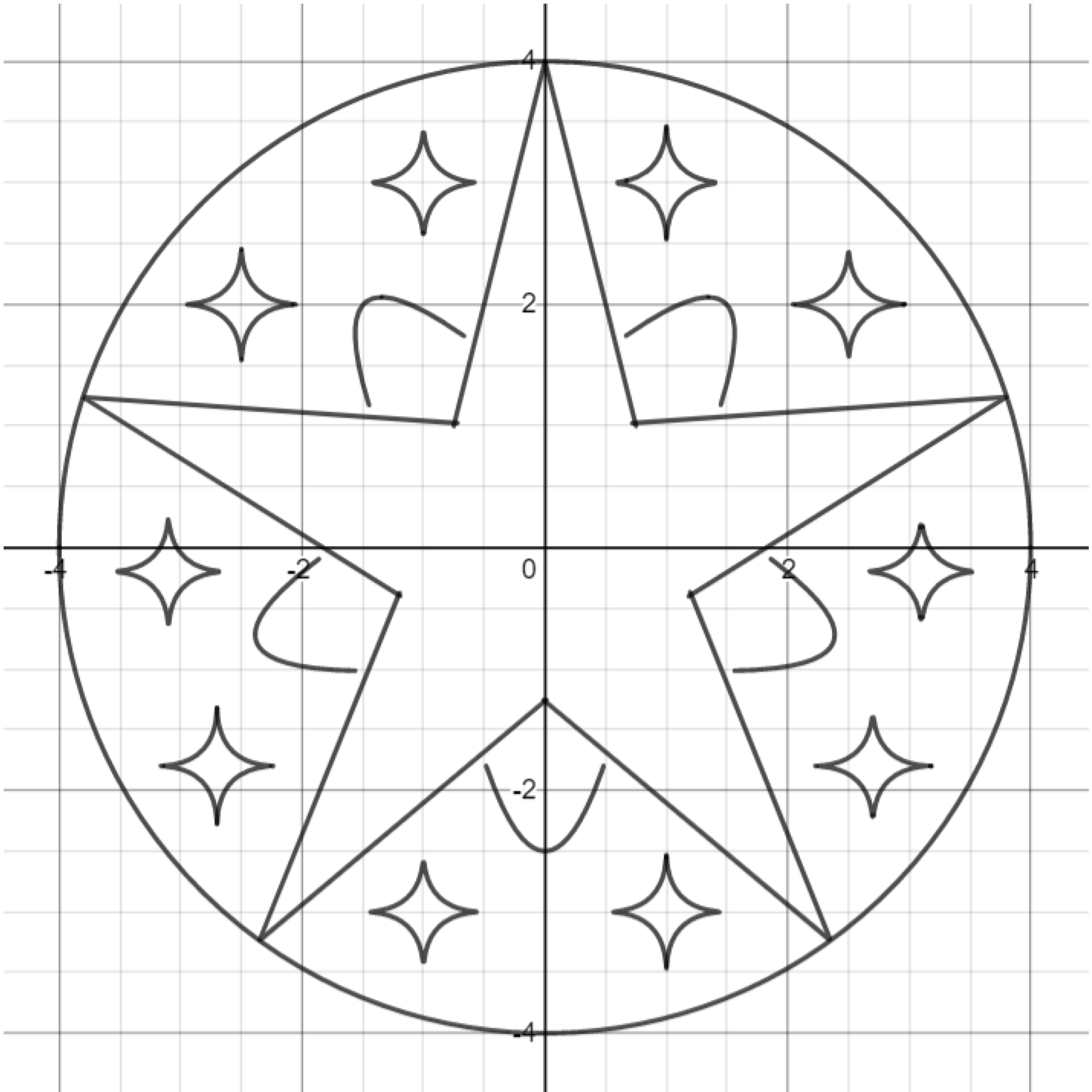
Challenge. Create your own emblem.
This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Rotation. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-rotation/