Graphing Calculator Drawing: Roots

by Justin Skycak (@justinskycak) on May 06, 2019

Roots can be used to draw deer.

This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Roots. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-roots/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Setup. Navigate to https://www.desmos.com/calculator. Be sure to sign in so that you can save your graph.

Demonstration - Root Graph. Observe the graph as you type each of the following inputs. In general, the graph $y=m\sqrt{x-a}$ makes an “r” shape that is shifted right $a$ units and stretched vertically by a factor of $m.$

$\begin{align*} y&=\sqrt{x} \\[10pt] y&=5\sqrt{x} \\[10pt] y&=0.2\sqrt{x} \\[10pt] y&=\sqrt{x-2} \\[10pt] y&=\sqrt{x+3} \end{align*}$

Demonstration - Reflections. Observe the graph as you type each of the following inputs. In general, the graph $y=\sqrt{-(x-a)}$ is the graph of $y=\sqrt{x-a}$ reflected over the y-axis, and the graph of $y=-\sqrt{x-a}$ is the graph of $y=\sqrt{x-a}$ reflected over the x-axis.

$\begin{align*} y&=\sqrt{-x} \\[10pt] y&=\sqrt{-(x-2)} \\[10pt] y&=-\sqrt{x-5} \\[10pt] y&=-\sqrt{-(x-5)} \end{align*}$

Exercise. Reproduce the graph shown below using a square root function of the form $y=m\sqrt{x-a}+b.$ This will form the back of a “root deer.”

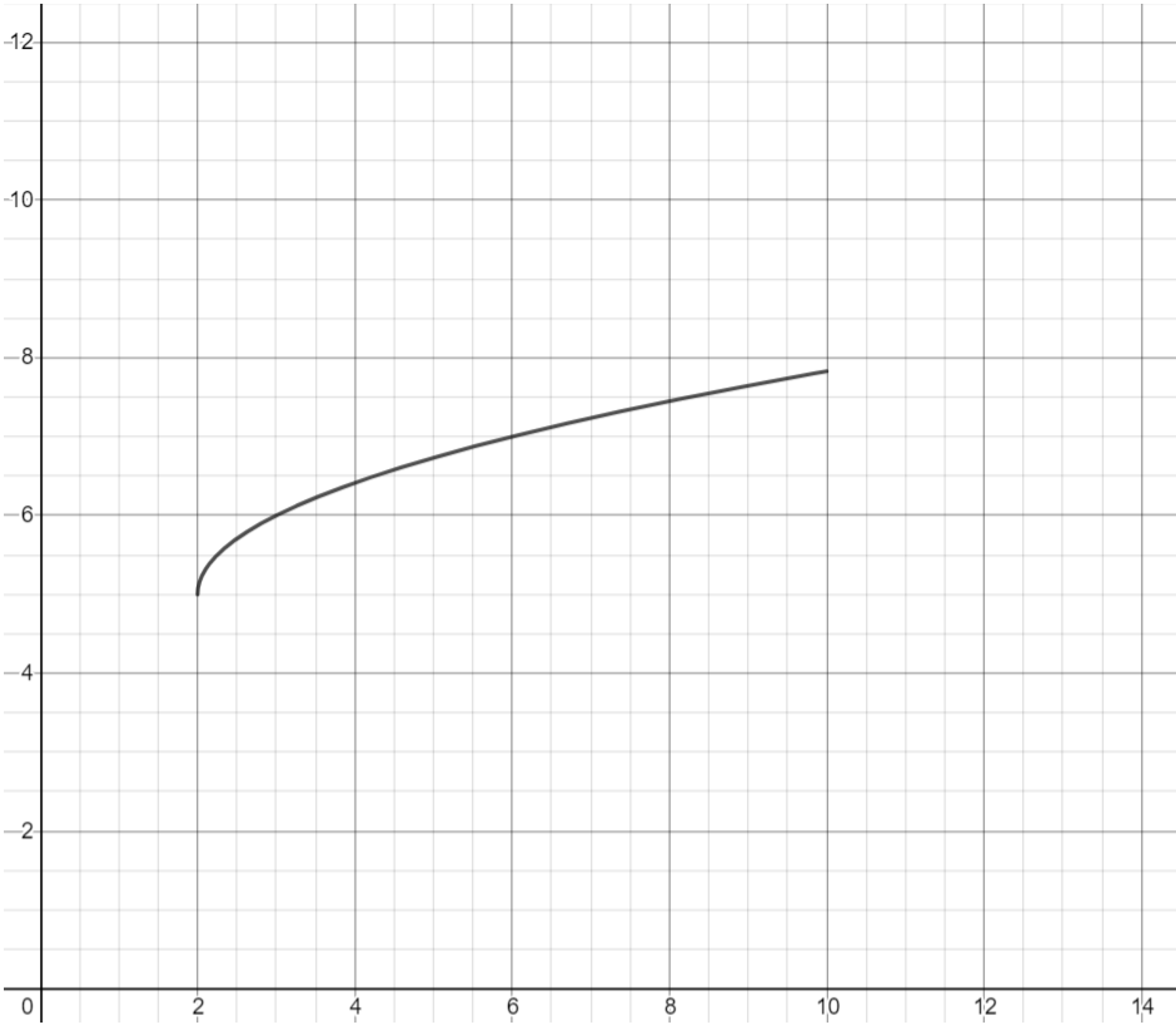
Exercise. Draw the back hip of the deer using a root function, and the back leg of the deer using a line.

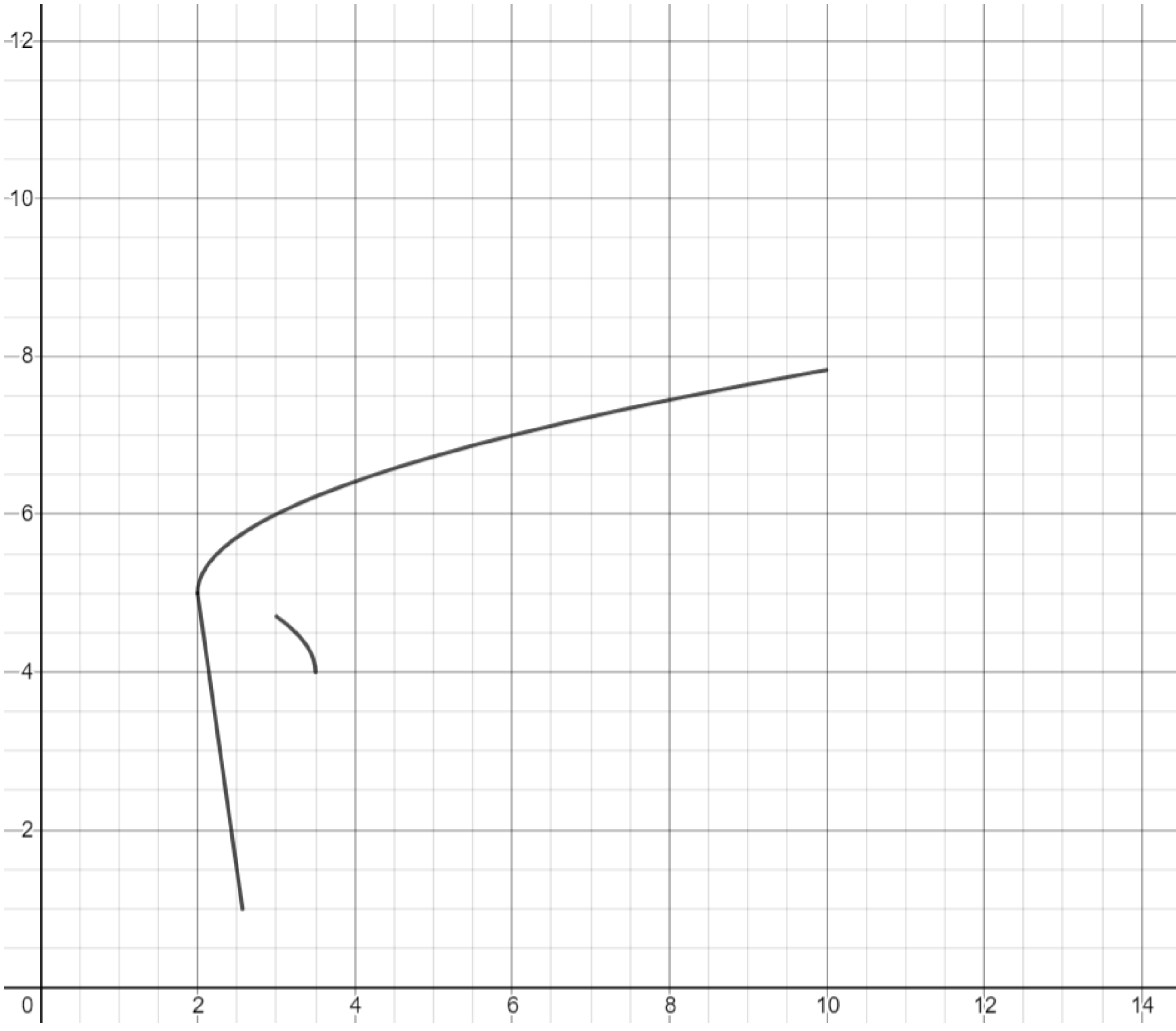
Exercise. Complete the back leg of the deer.

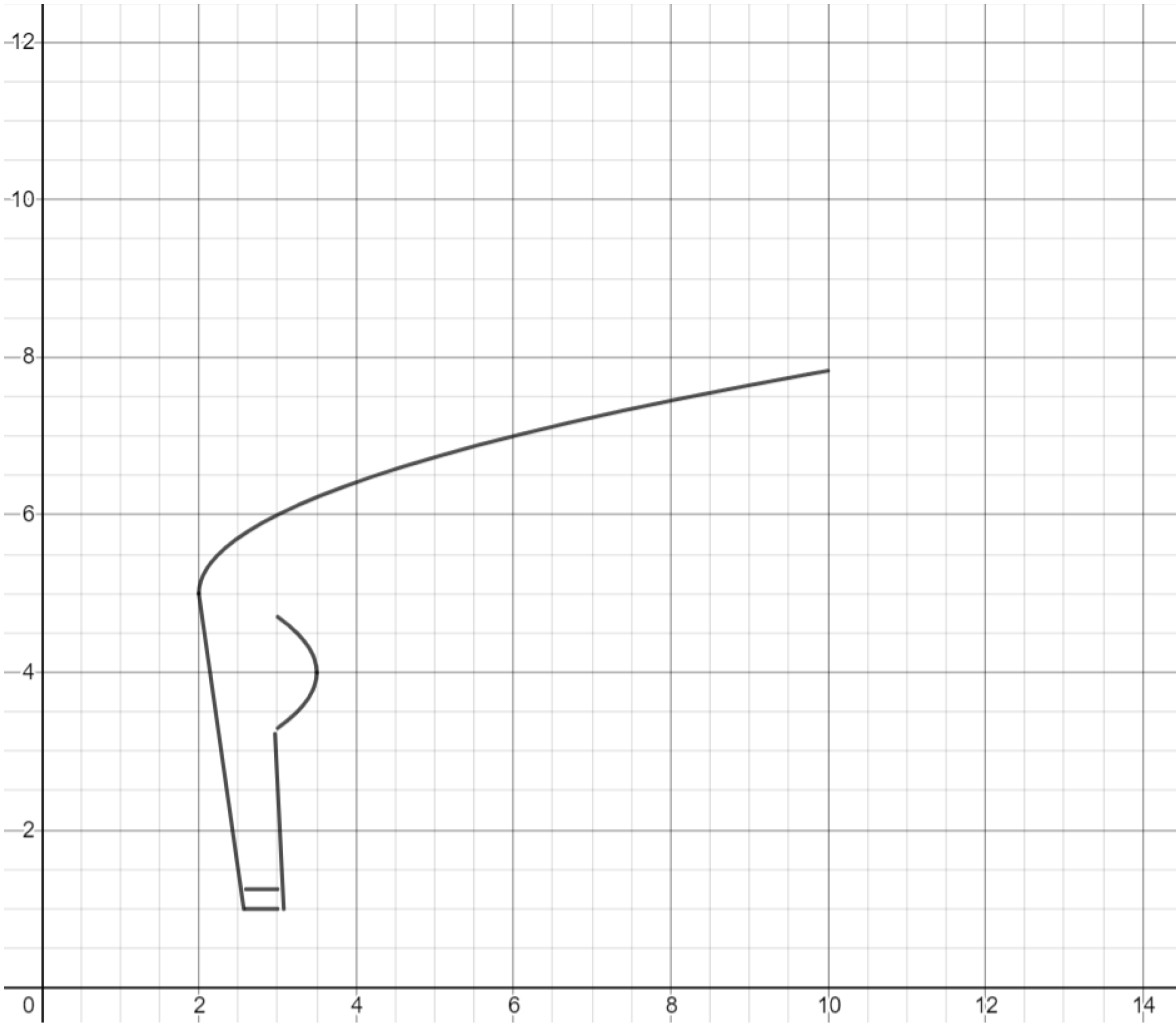
Exercise. Use another root function to draw the belly of the deer.

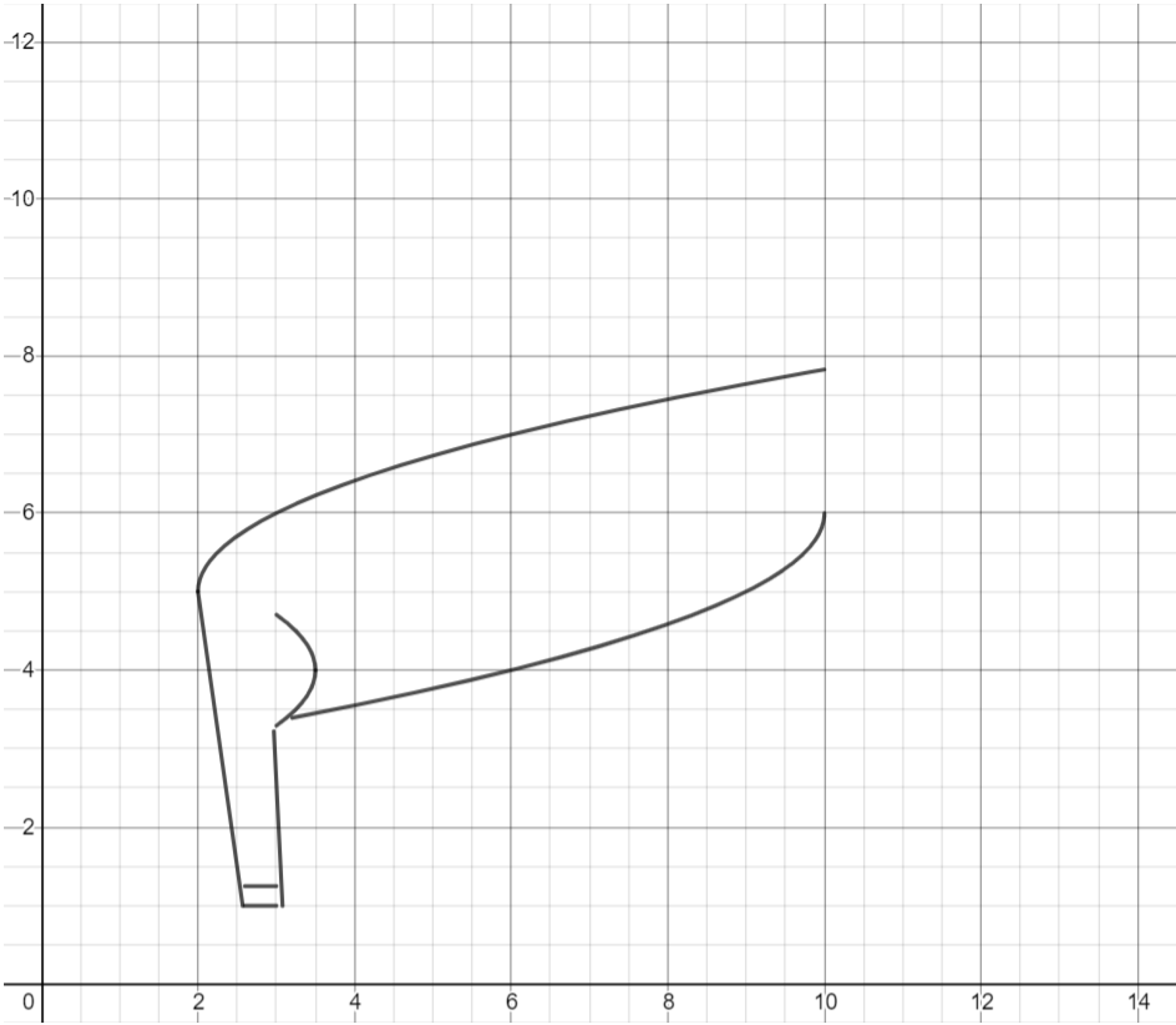
Exercise. Use lines and a parabola to draw the front leg of the deer.

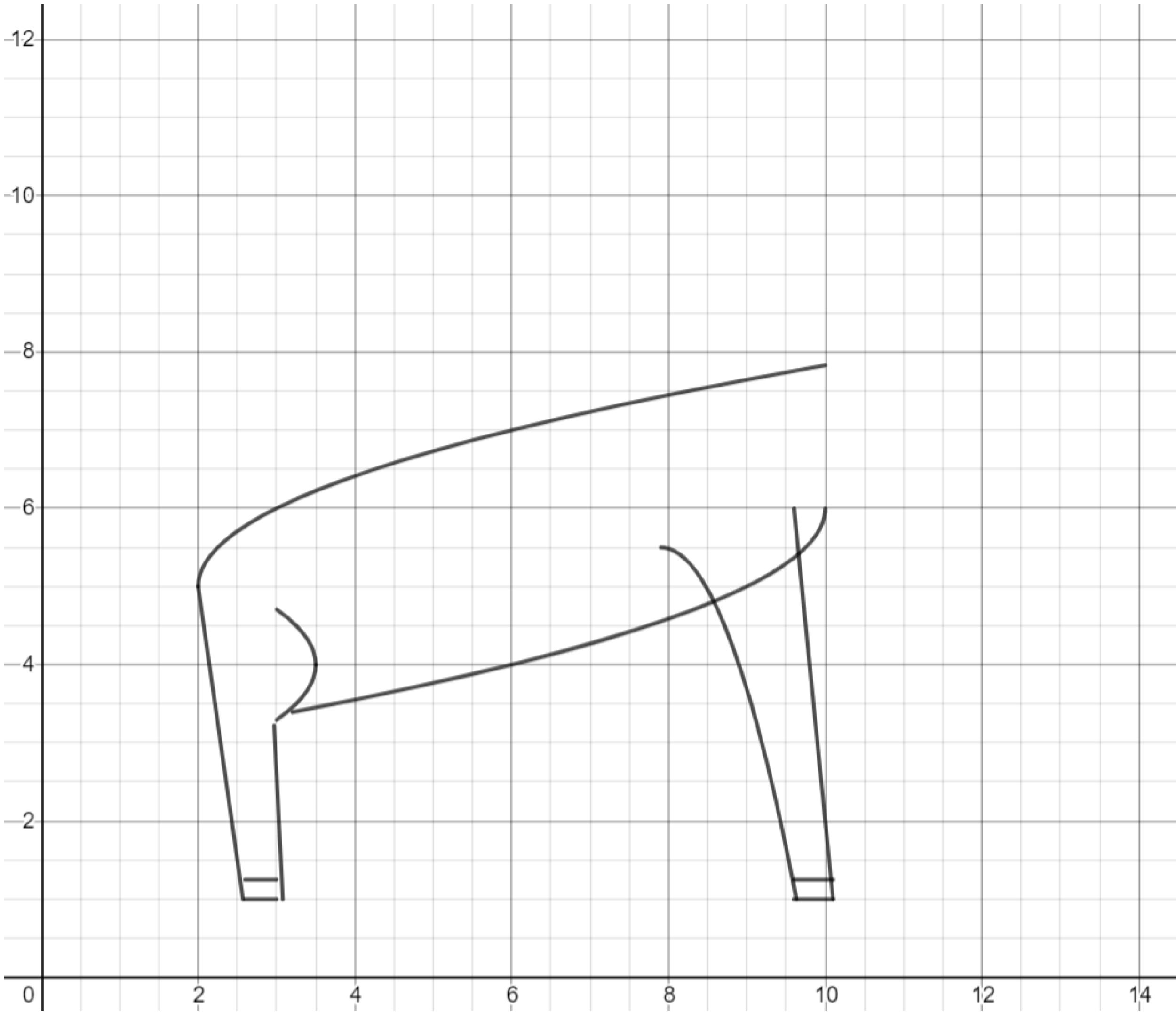
Exercise. Break the belly of the deer into two separate functions so that it does not cross over the deer’s front leg.

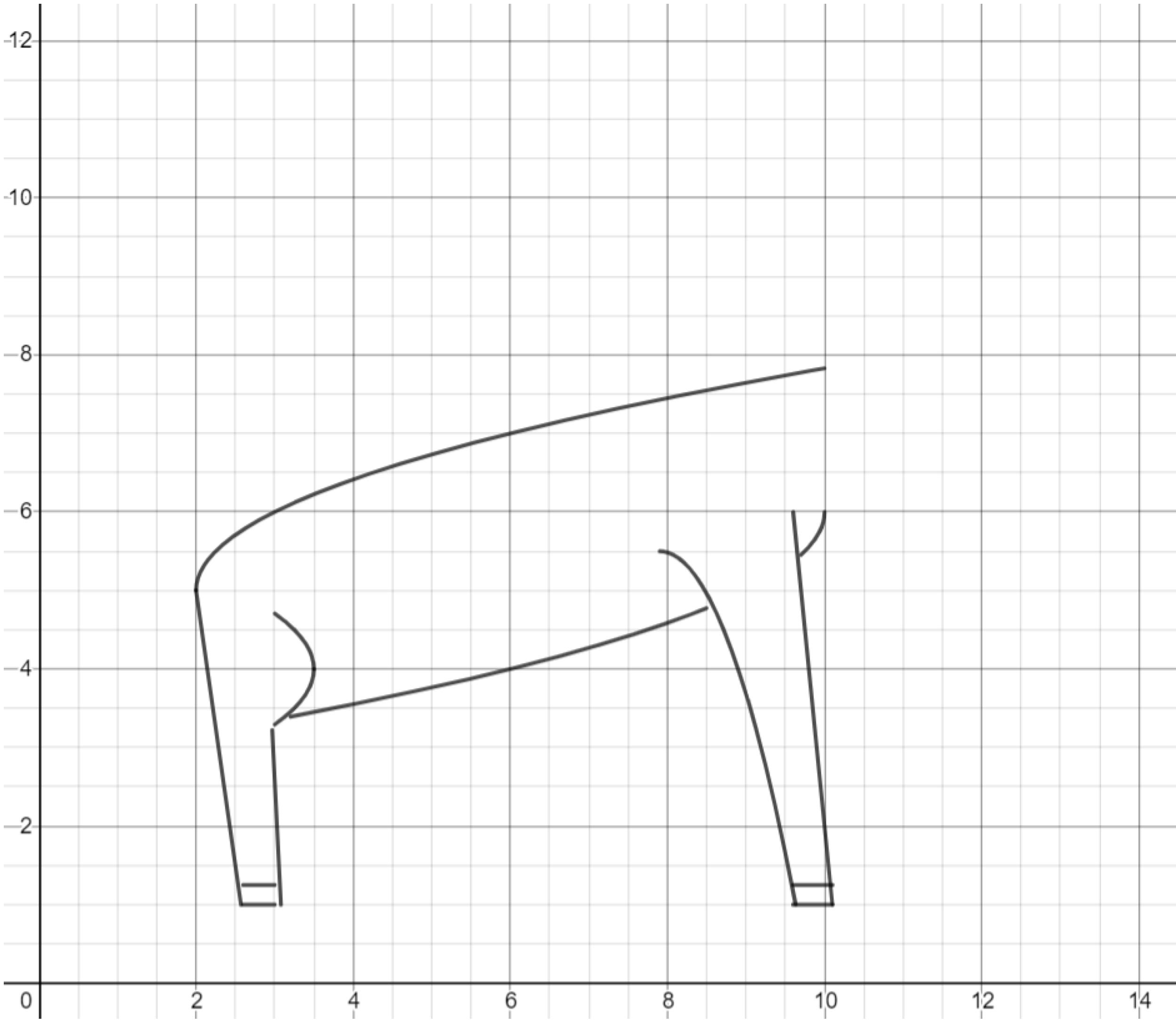
Exercise. Draw the head of the deer using two root functions.

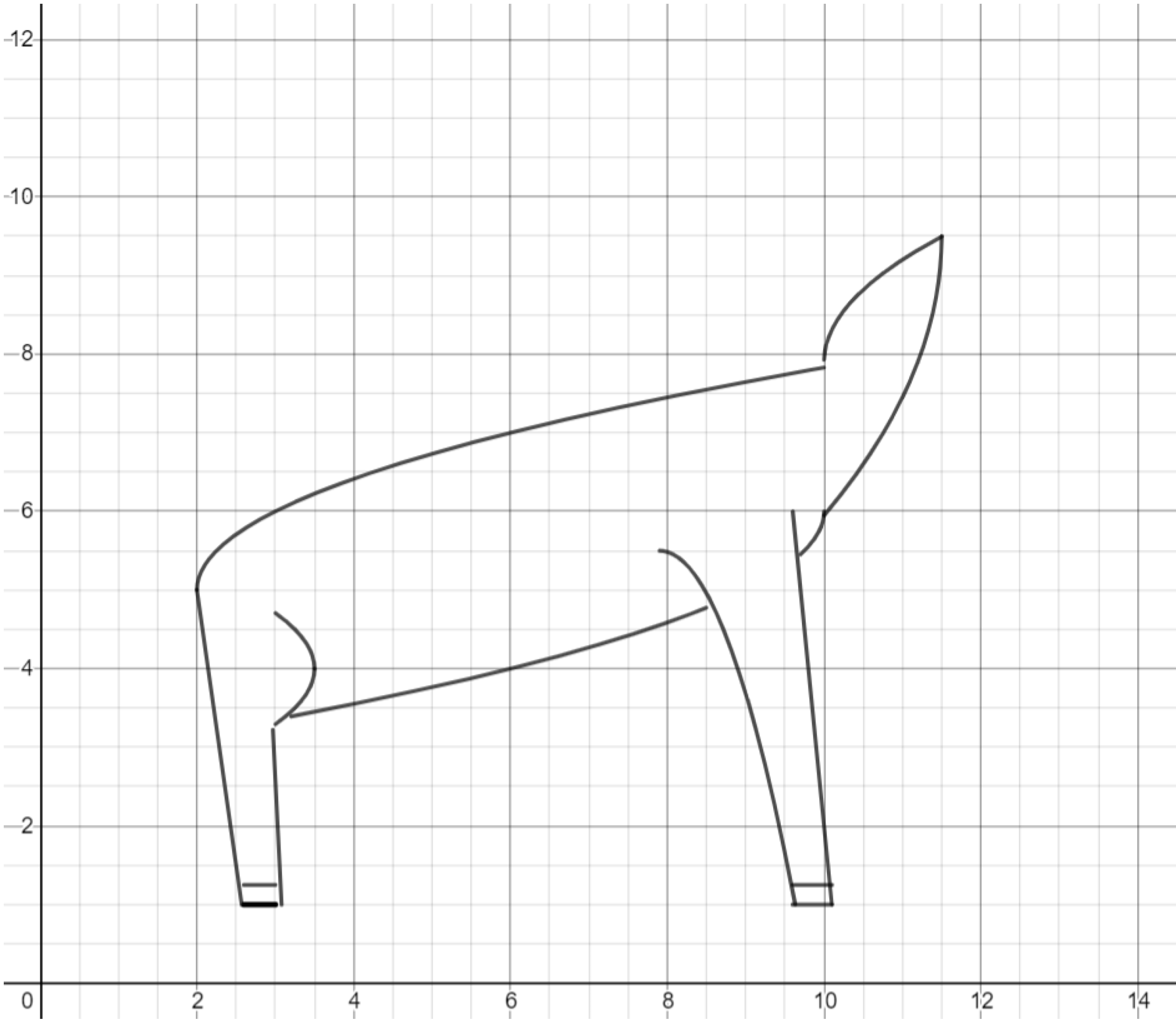
Exercise. Draw antlers on the deer. You can use a root function for the upper antler, and a parabola for the lower antler.

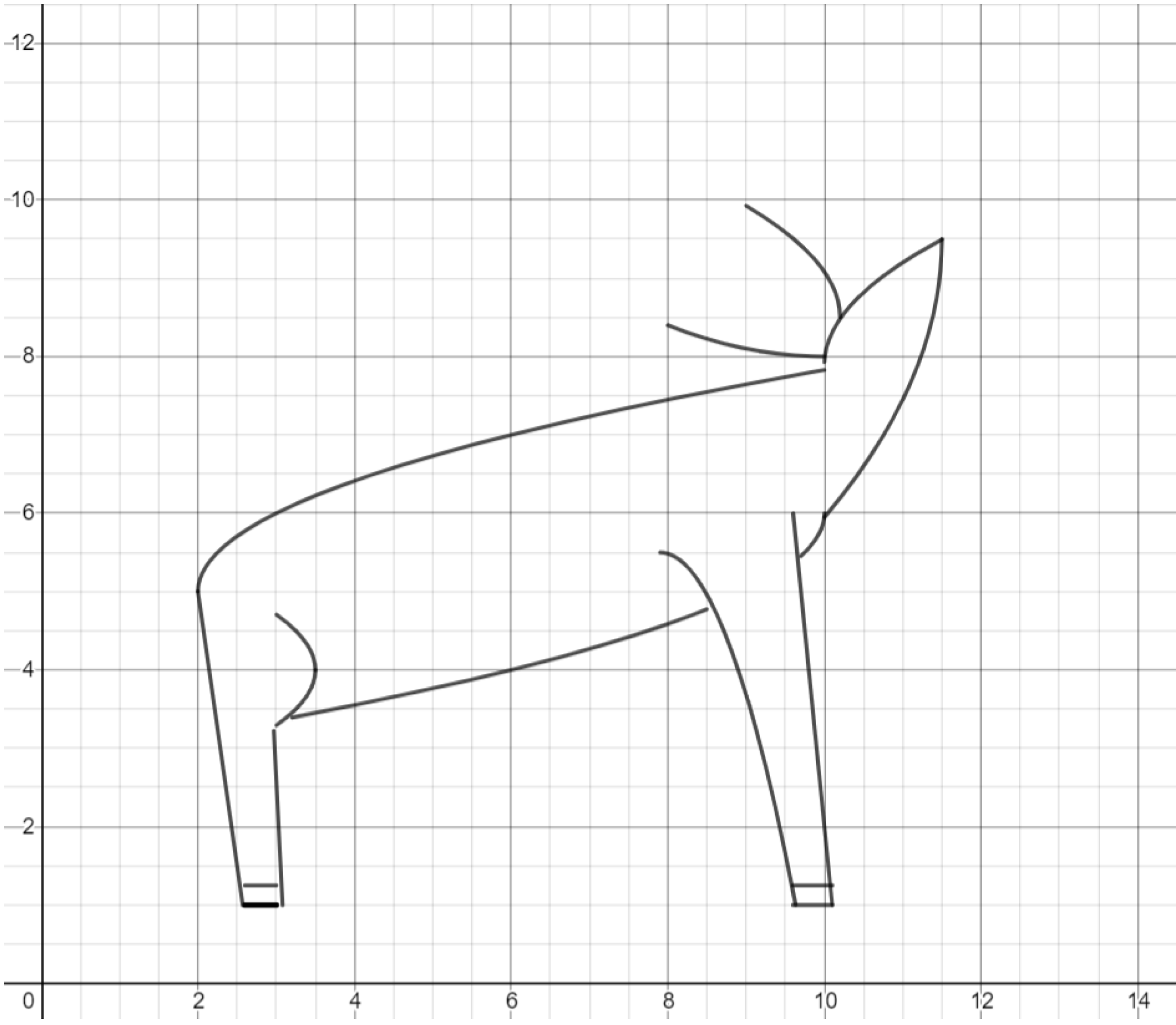
Exercise. Use a root function to draw an upper branch of antlers on each of the antlers previously drawn.

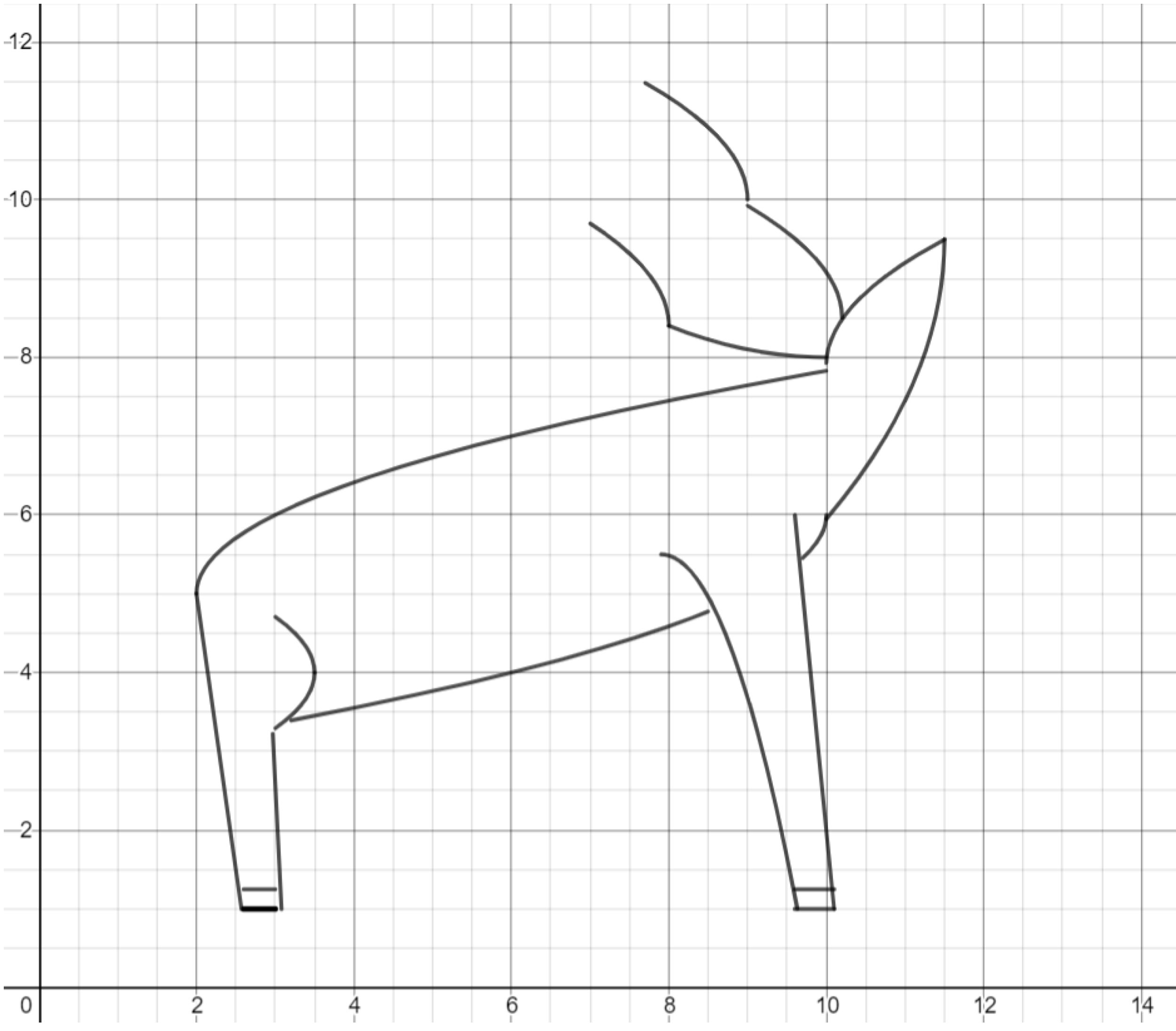
Exercise. Use a parabola to draw a lower branch of antlers below each of the antlers previously drawn.

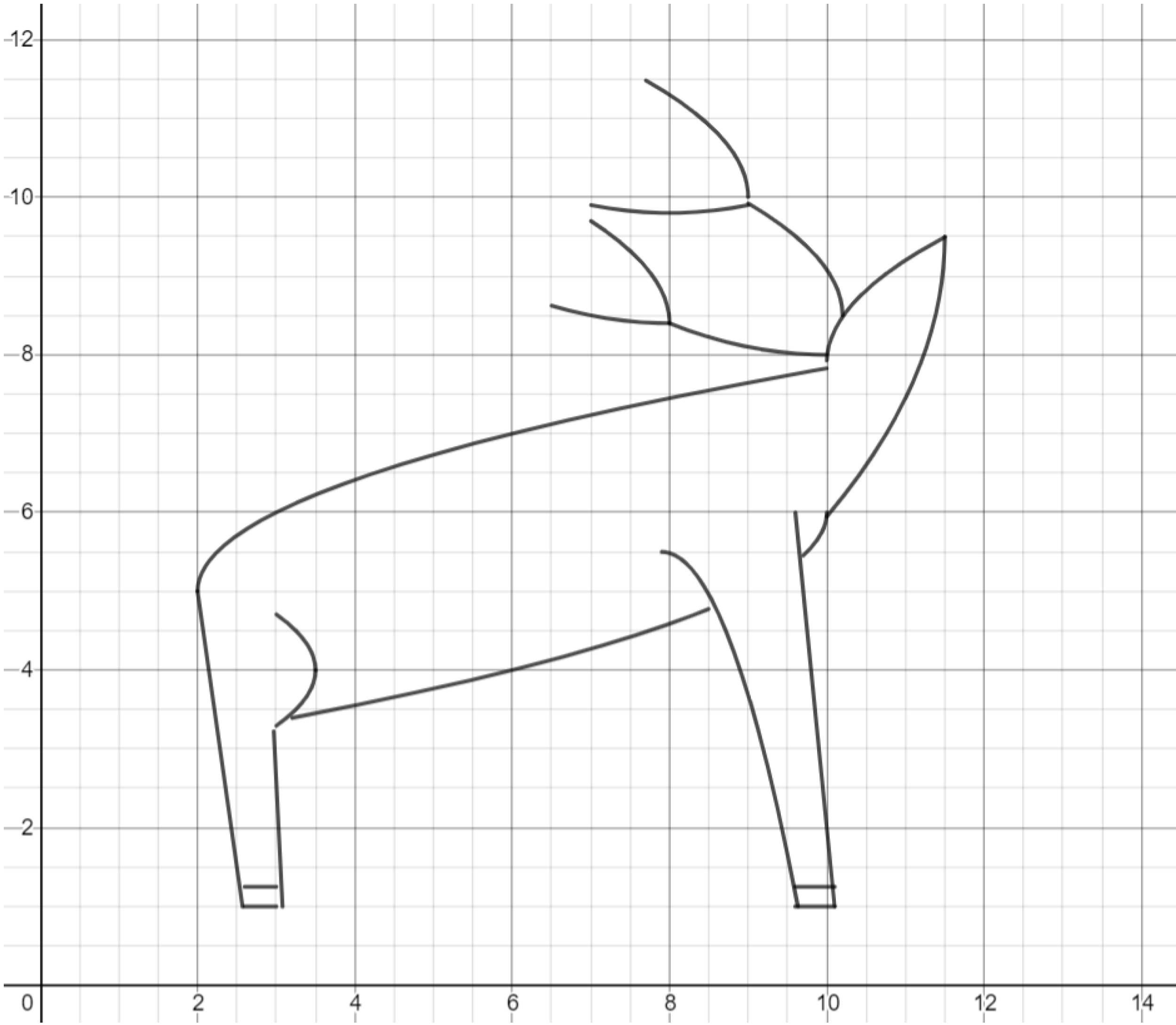
Exercise. Use lines and a parabola to complete the face of the deer.

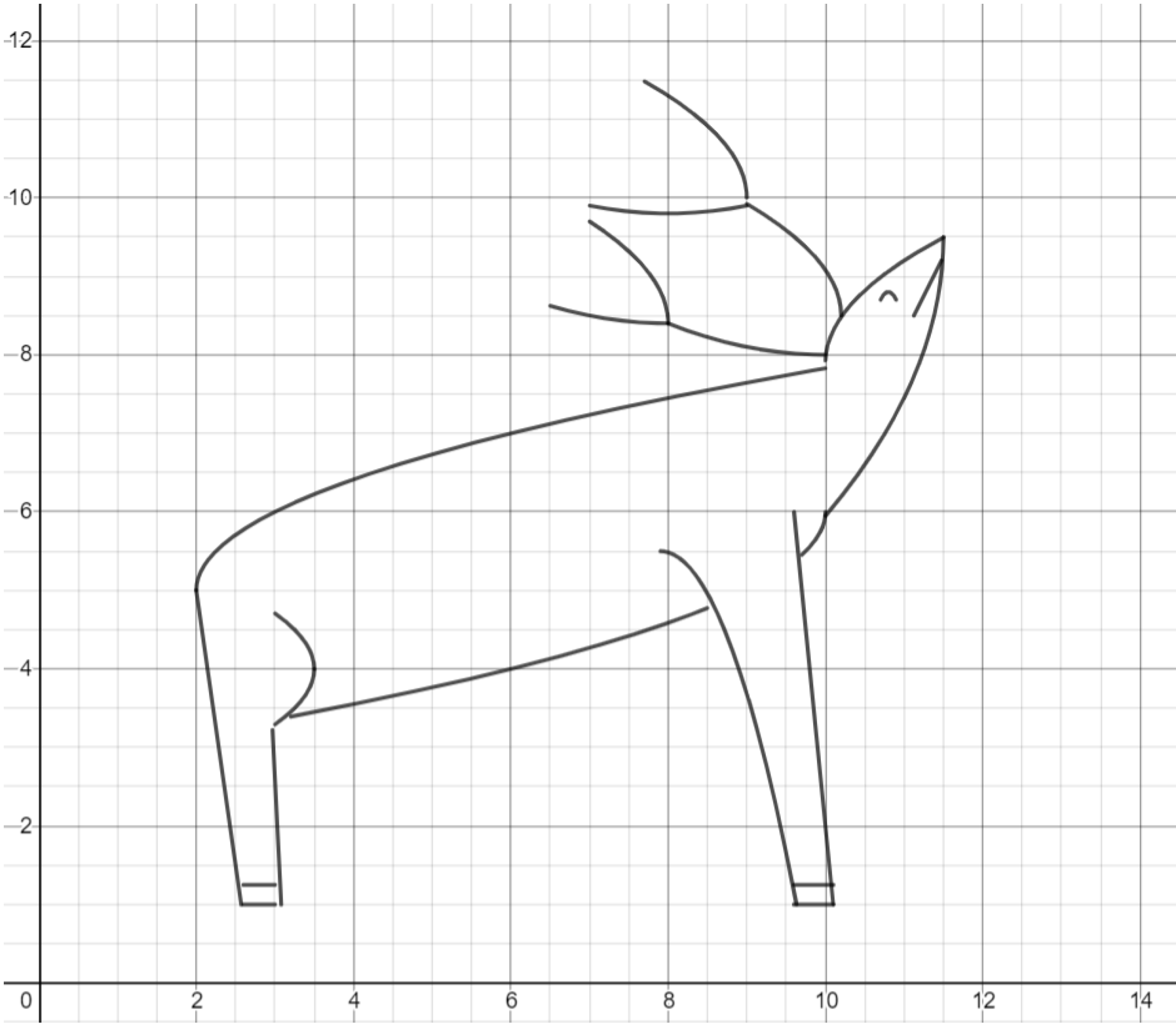
Challenge. Draw another woodland creature, such as a hedgehog.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.