Graphing Calculator Drawing: Parabolas

by Justin Skycak (@justinskycak) on May 04, 2019

Parabolas can be used to draw a fish.

This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Parabolas. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-parabolas/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Setup. Navigate to https://www.desmos.com/calculator. Be sure to sign in so that you can save your graph.

Demonstration - Parabola. Observe the graph as you type each of the following inputs. In general, an absolute value graph $y=mx^2$ makes a “U” shape, with the magnitude of $m$ controlling the slope of the U, and the sign of $m$ controlling whether the U opens upward or downward.

$\begin{align*} y&=5x^2 \\[10pt] y&=1x^2 \\[10pt] y&=0.1x^2 \\[10pt] y&=-0.1x^2 \\[10pt] y&=-1x^2 \\[10pt] y&=-5x^2 \end{align*}$

Demonstration - Shifts. Observe the graph as you type each of the following inputs. In general, the graph of $y=m(x-a)^2+b$ shifts the absolute value graph $y=mx^2$ so that the hump of the “U” occurs at the point $(a,b).$

$\begin{align*} y&=(x-1)^2+2 \\[10pt] y&=-2(x-1)^2-3 \\[10pt] y&=-0.5(x+3)^2-1 \\[10pt] y&=10(x+2)^2+1 \end{align*}$

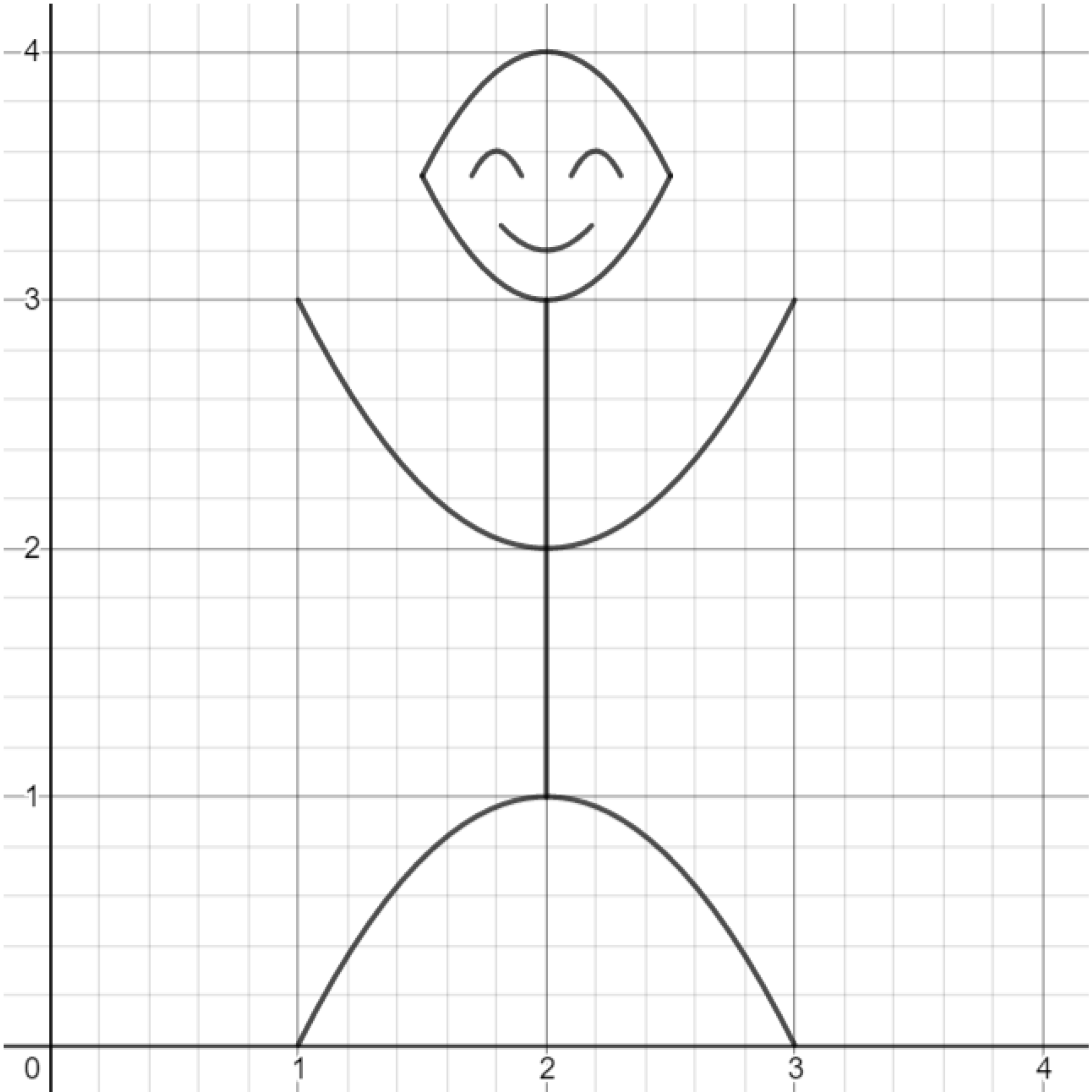
Exercise. Previously, you used absolute value functions to create a person. This time, draw the person using parabolas!

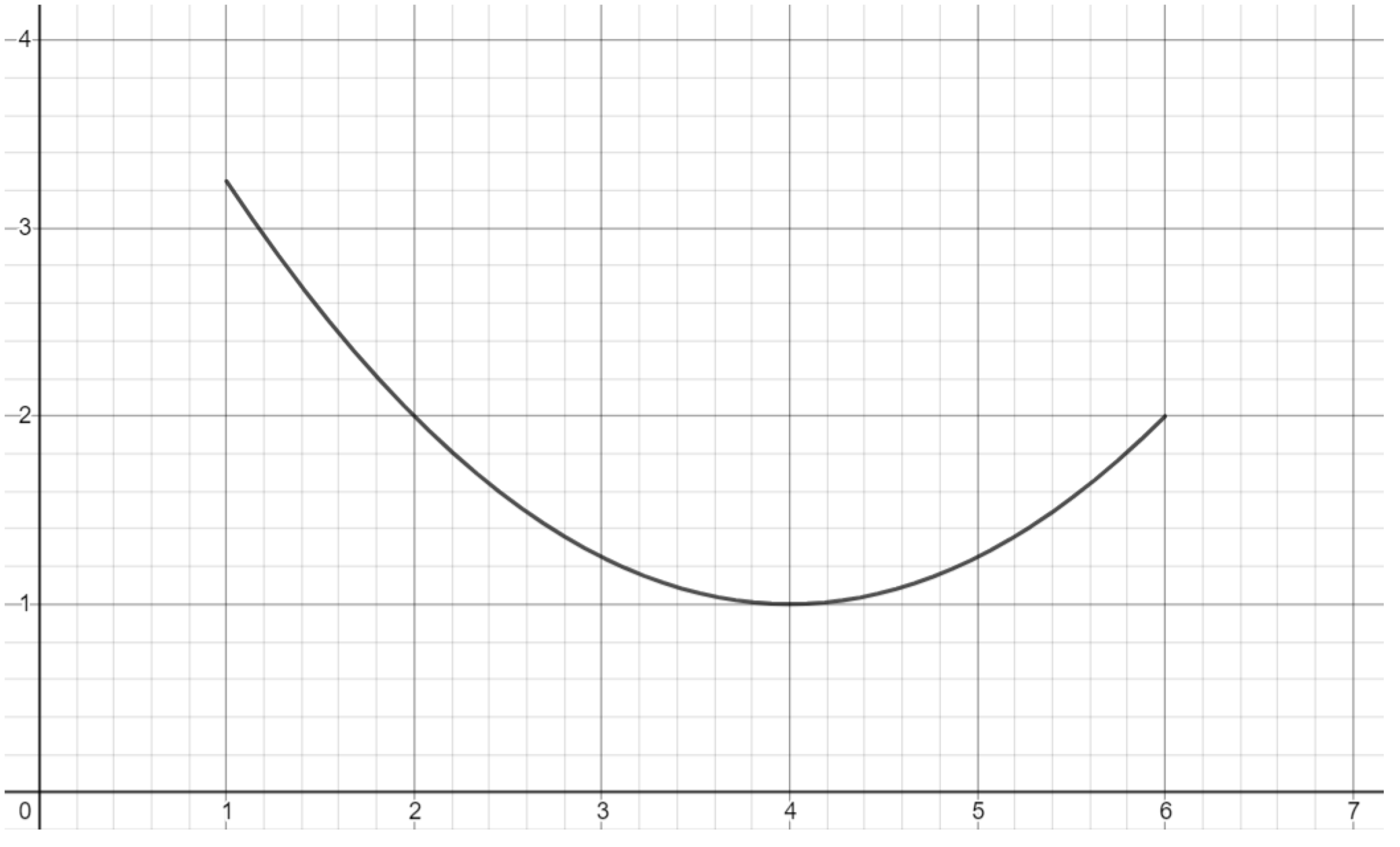
Exercise. Draw the portion of the parabola shown below.

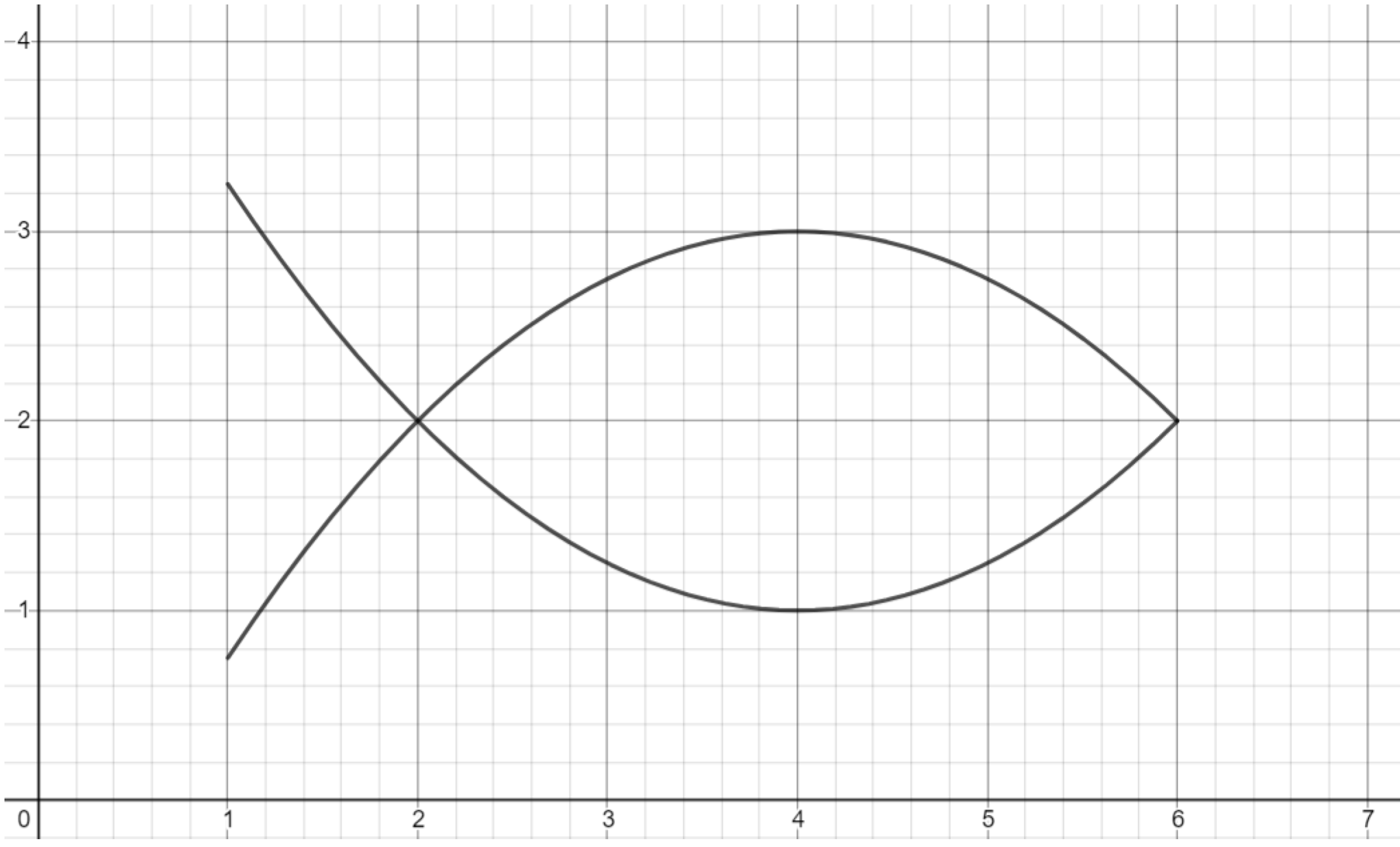
Exercise. Reflect and shift a copy of the parabola portion drawn previously to form an outline of a fish.

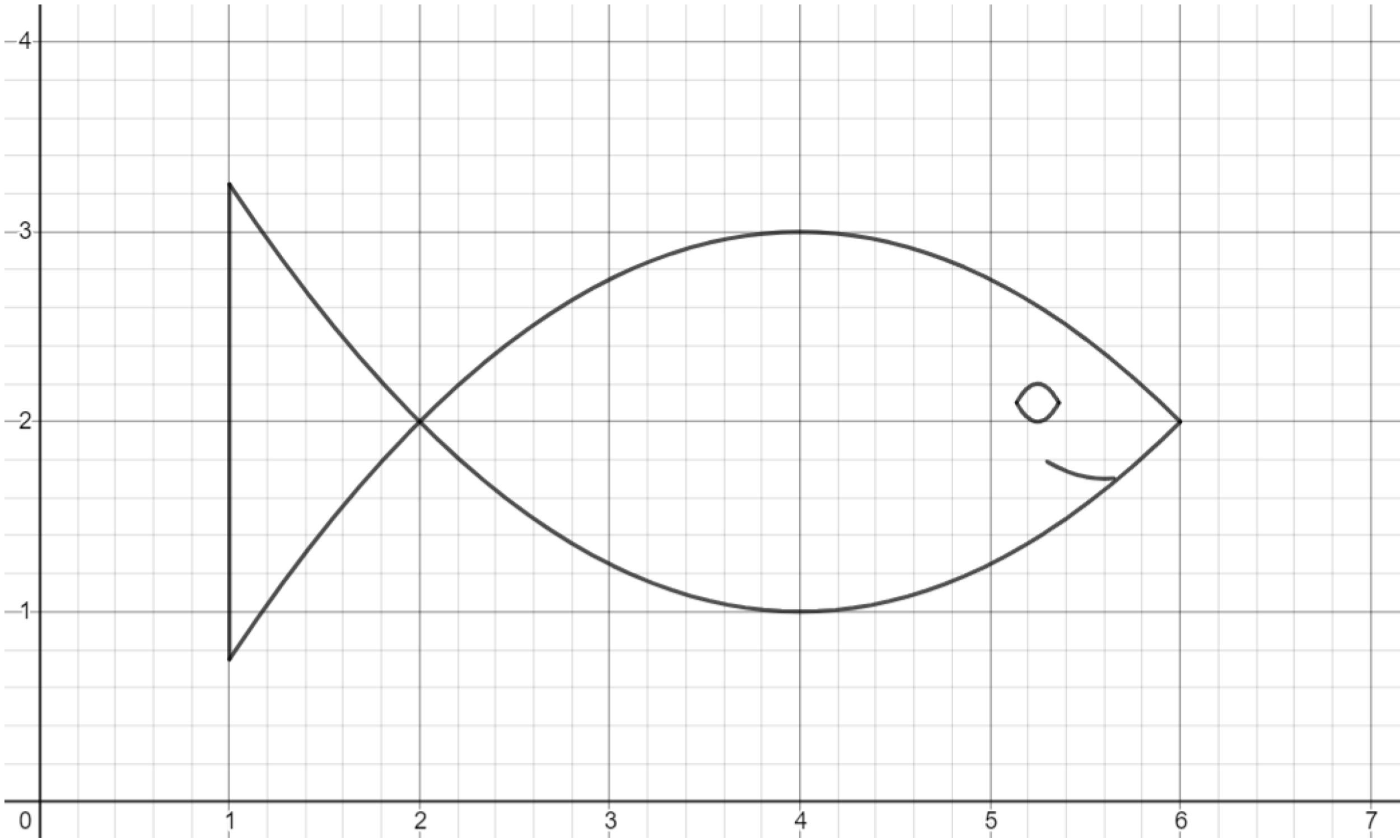
Exercise. Complete the final details of the fish.

Challenge. Draw a school of fish! You can try to include other sea creatures, as well.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.