Graphing Calculator Drawing: Non-Euclidean Ellipses

by Justin Skycak (@justinskycak) on May 09, 2019

Non-euclidean ellipses can be used to draw starry-eye sunglasses.

This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Non-Euclidean Ellipses. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-non-euclidean-ellipses/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Setup. Navigate to https://www.desmos.com/calculator. Be sure to sign in so that you can save your graph.

Demonstration - Non-Euclidean Circles. Observe the graph as you type each of the following inputs. In general, the graph of the unit circle is given by $\vert x\vert^n+ \vert y \vert^n=1.$ For $n=2,$ this makes a Euclidean circle, i.e. all those points whose distance from the origin is 1, where distance is measured by the Euclidean metric $\sqrt{x^2+y^2}.$ For other values of $n,$ these equations make non-Euclidean circles, i.e. all the points whose “distance” from the origin is 1, where distance is measured by the metric $\sqrt[n]{\vert x \vert^n+ \vert y\vert^n}.$

$\begin{align*} &|x|^4+|y|^4=1 \\[10pt] &|x|^3+|y|^3=1 \\[10pt] &|x|^2+|y|^2=1 \\[10pt] &|x|^1+|y|^1=1 \\[10pt] &|x|^{0.8}+|y|^{0.8}=1 \\[10pt] &|x|^{0.5}+|y|^{0.5}=1 \\[10pt] &|x|^{0.2}+|y|^{0.2}=1 \end{align*}$

Demonstration - Non-Euclidean Ellipses. Observe the graph as you type each of the following inputs. In general, the graph of $\left\vert \frac{x-a}{A} \right\vert^n + \left\vert \frac{y-b}{B} \right\vert^n = 1$ makes an ellipse with horizontal radius $A$ and vertical radius $B$ centered at the point $(a,b).$ When $n \neq 2,$ this is a non-Euclidean ellipse.

$\begin{align*} &\left| \frac{x-0}{1} \right|^{10}+\left| \frac{y-0}{2} \right|^{10}=1 \\[10pt] &\left| \frac{x-3}{2} \right|^{0.8}+\left| \frac{y-5}{5} \right|^{0.8}=1 \end{align*}$

Exercise. Reproduce the graph shown below using non-Euclidean circles.

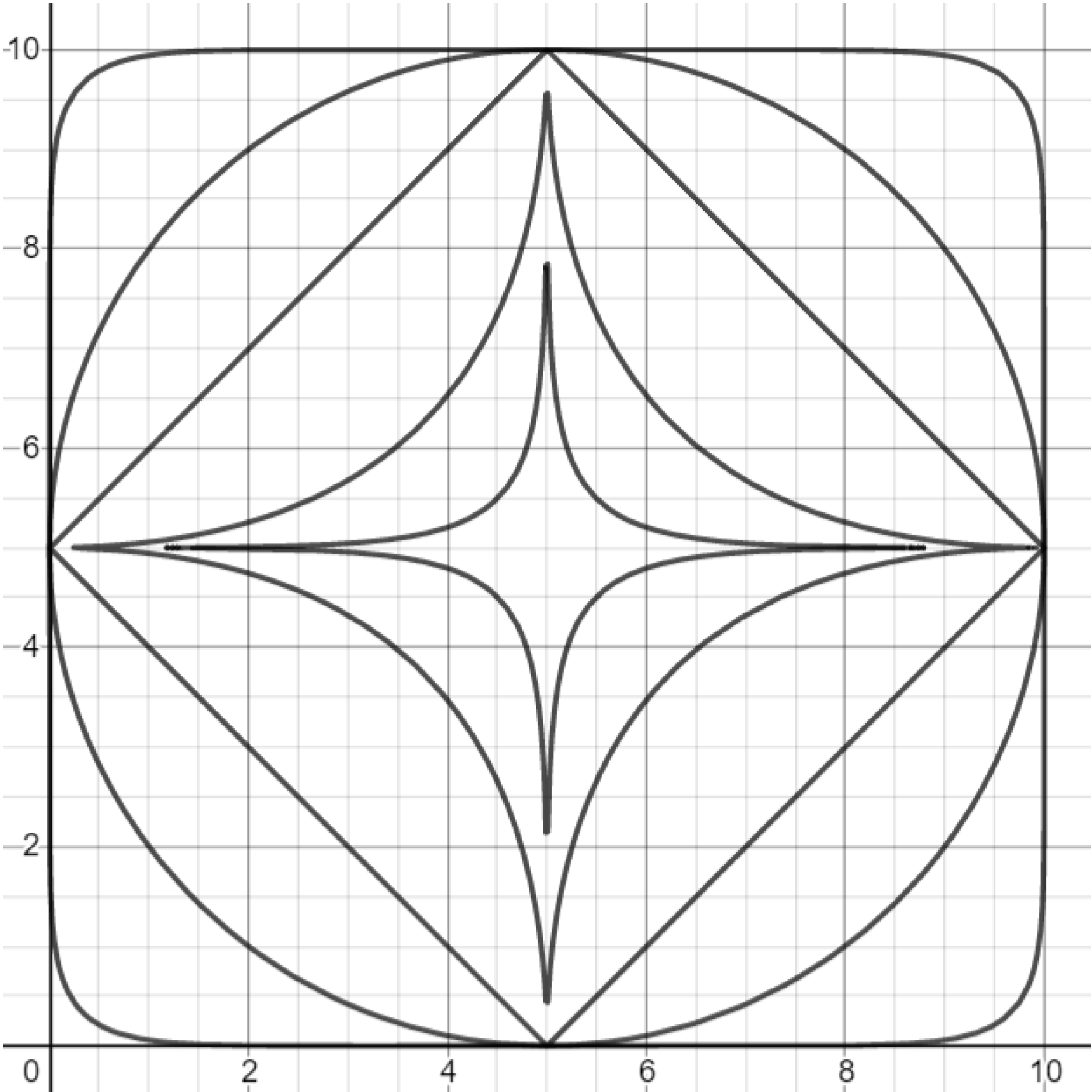
Exercise. Change the non-Euclidean circles to non-Euclidean ellipses in the previous exercise to reproduce the graph shown below.

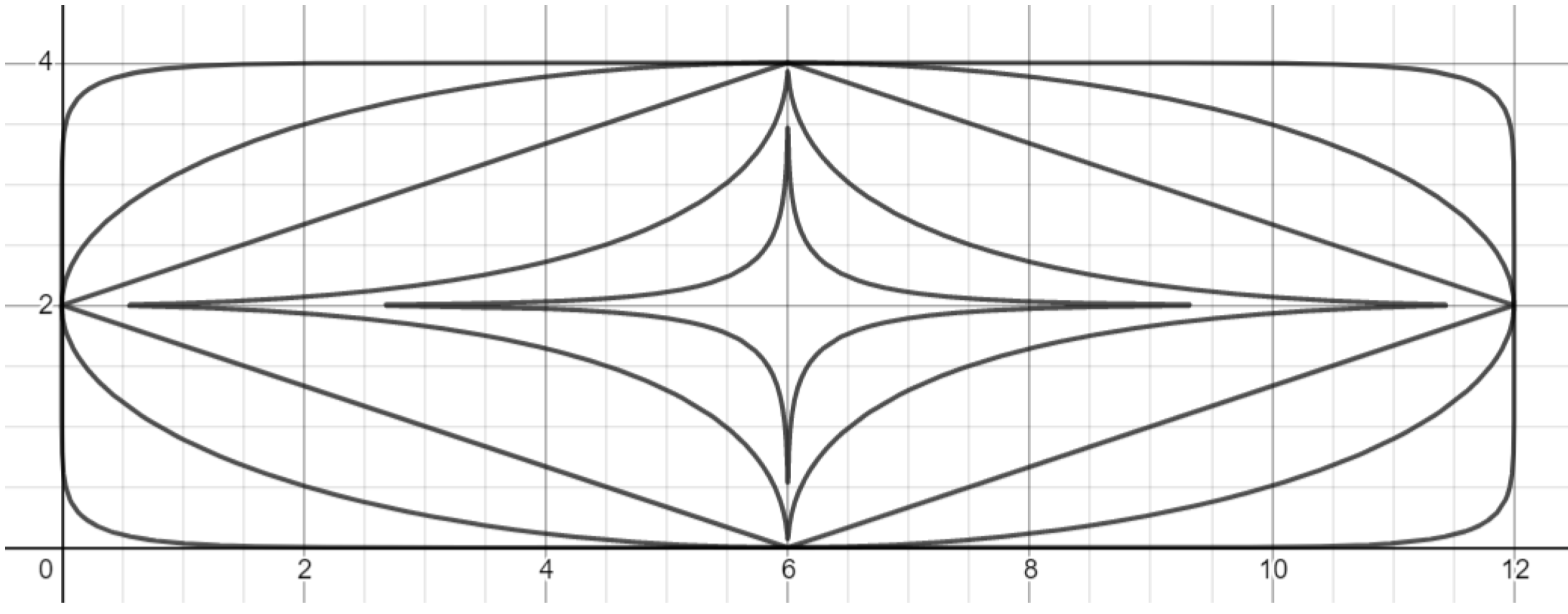
Exercise. Shift the ellipses right and up to produce the graph below.

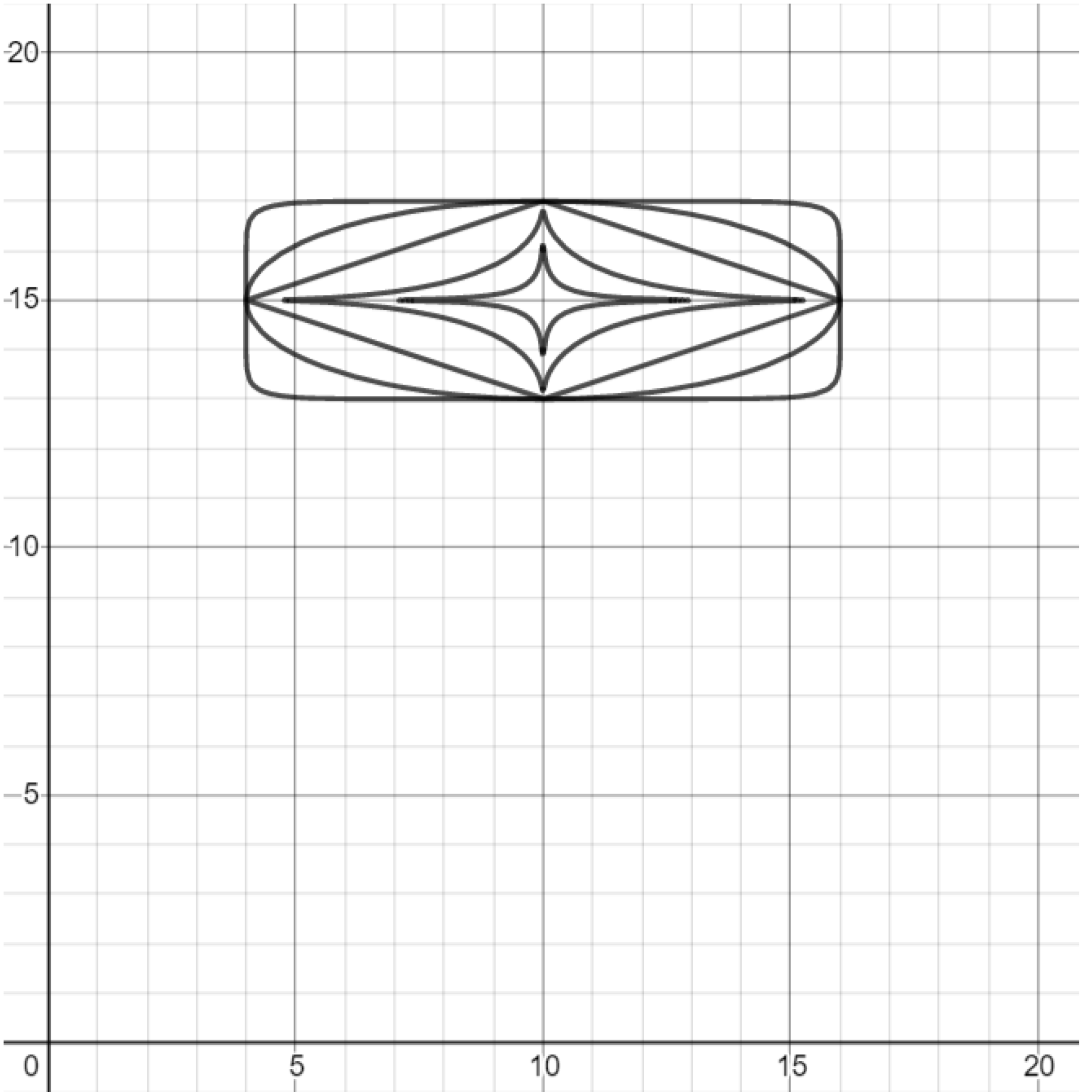
Exercise. Create another set of ellipses, shifted right of the original set.

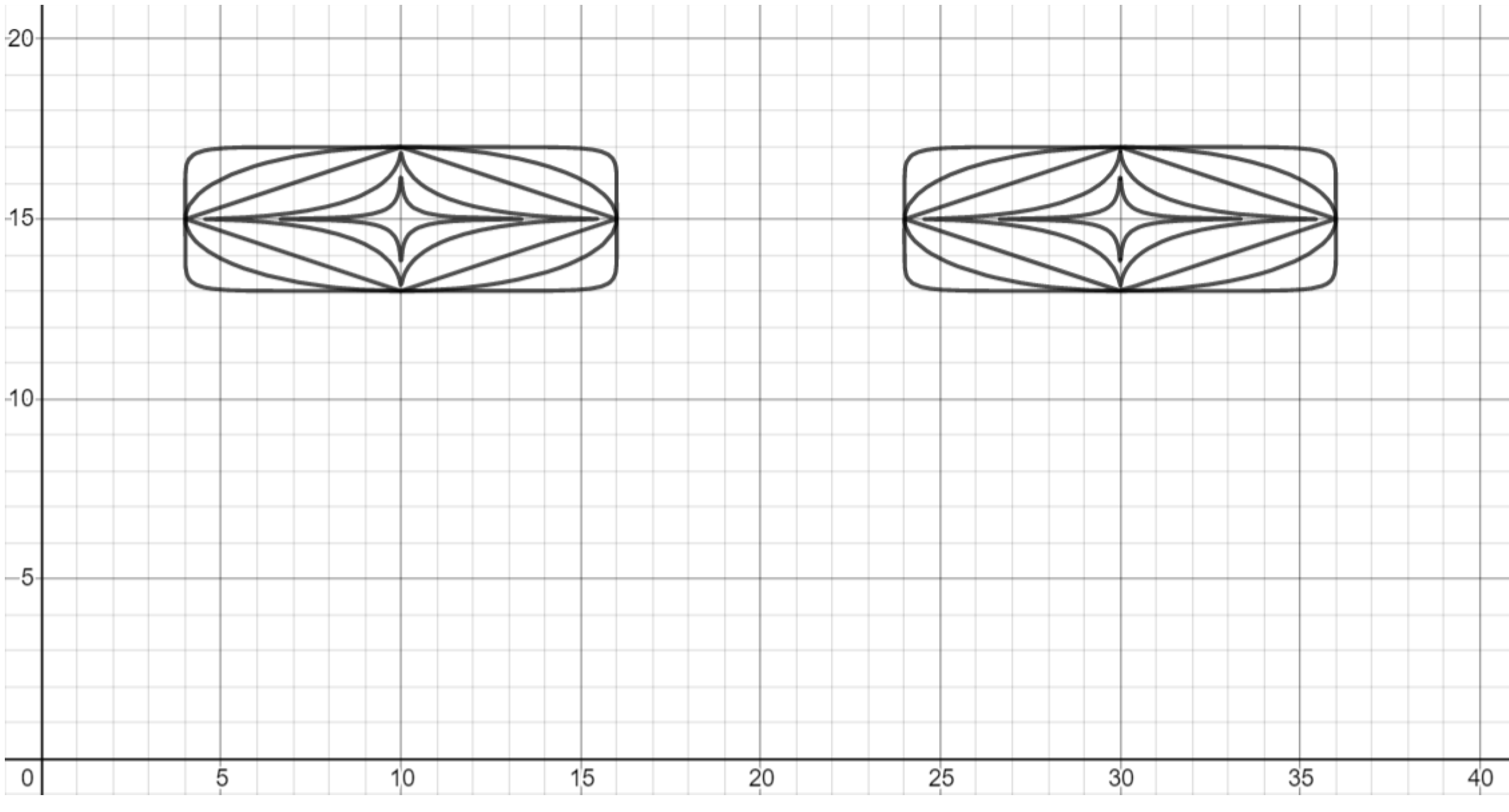
Exercise. Add some details to form a face. The head can be made using a non-Euclidean ellipse, the frame of the glasses can be made using a parabola and two lines, and the smile can be made using a parabola with sine shading.

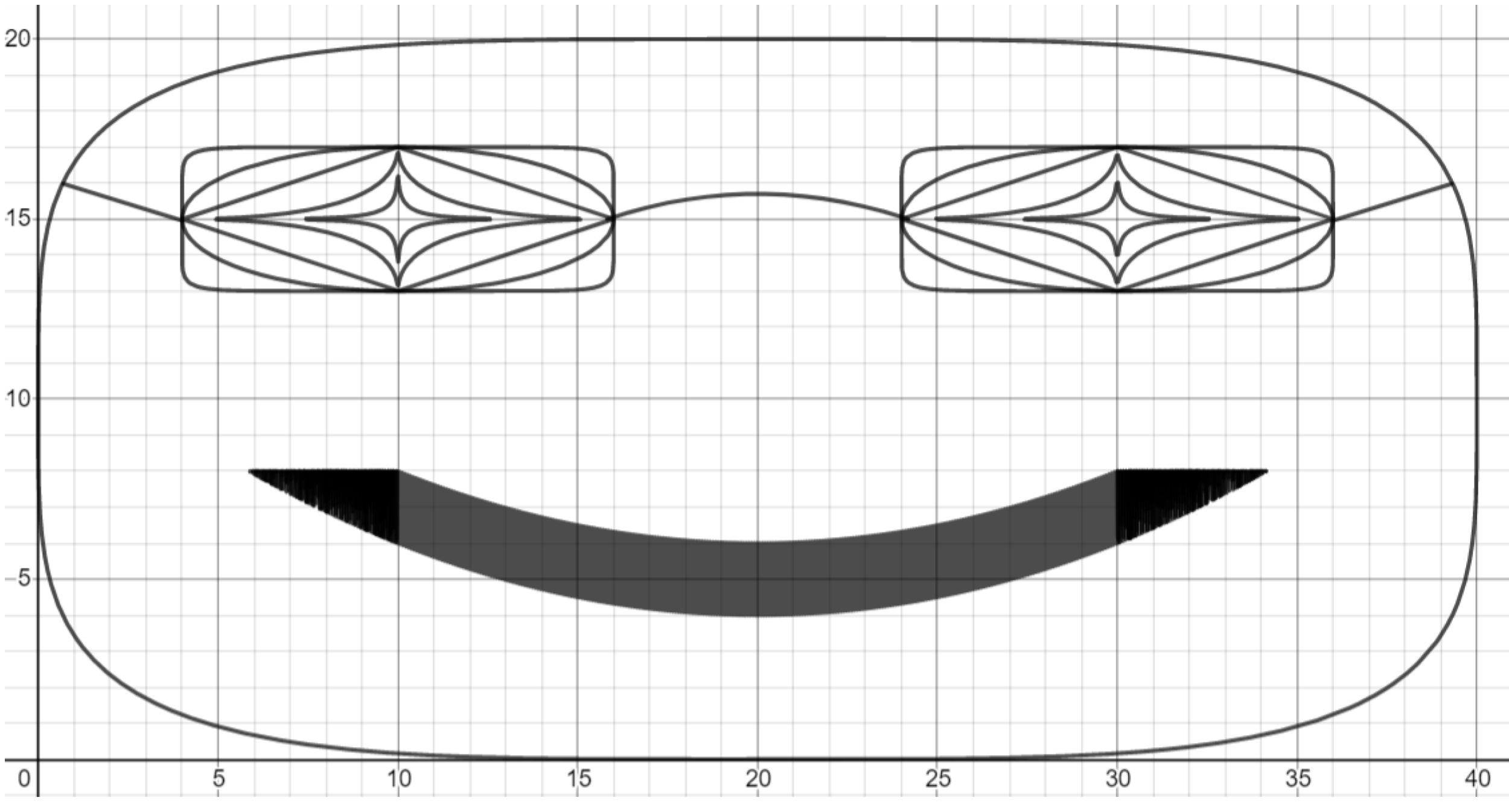
Exercise. Lastly, add some hair on the head. You can do this by duplicating the biggest ellipse that outlines the face, restricting the range, and shading via sine.

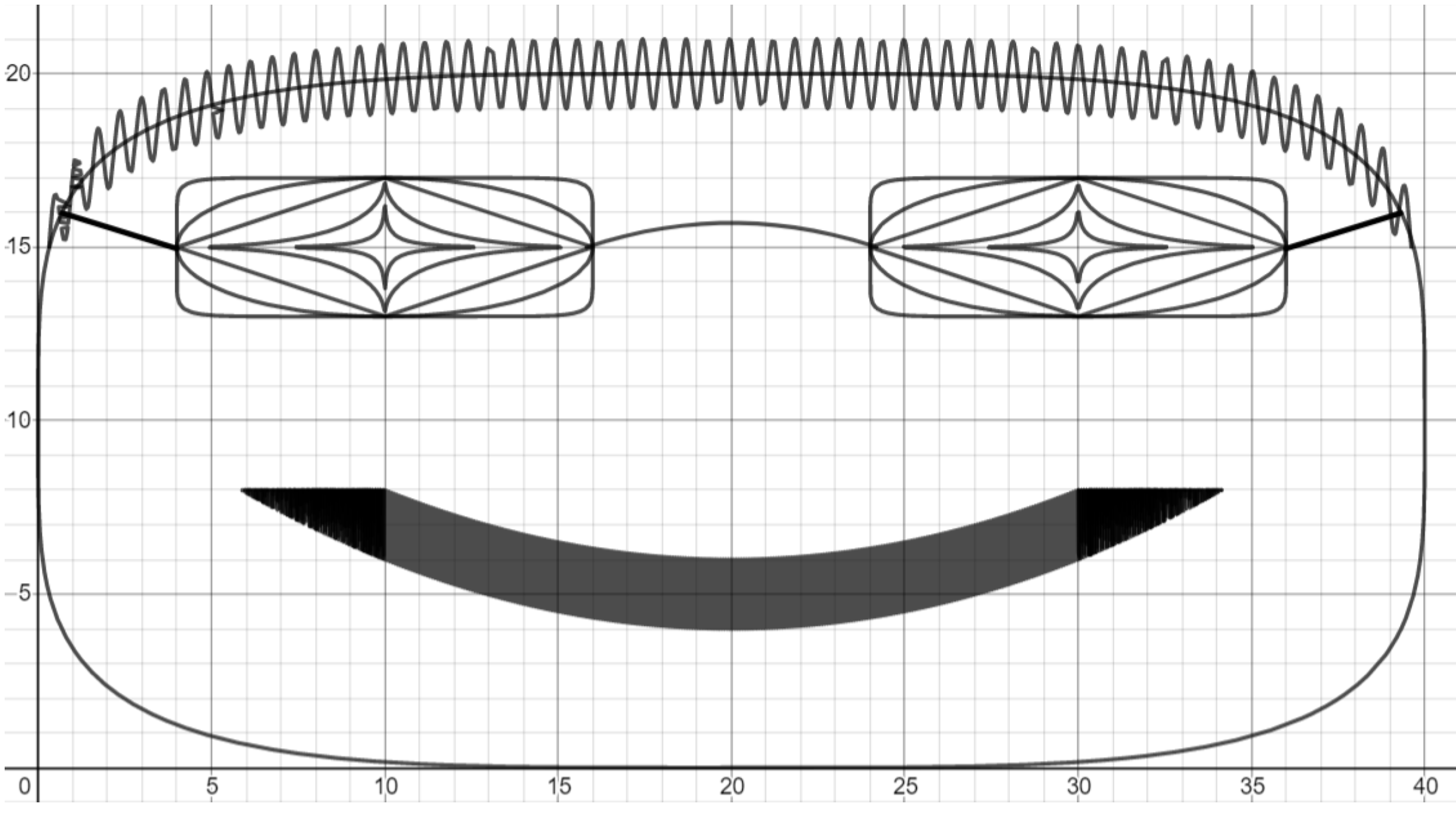
Challenge. Try to make a narrower face with longer hair.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.