Graphing Calculator Drawing: Lissajous Curves

May 11, 2019

This post is part of a series.

Setup. Navigate to https://www.desmos.com/calculator. Be sure to sign in so that you can save your graph.

Demonstration - Lissajous Curves. Lissajous curves take the form

$\begin{align*} x &= \sin(t) \\[5pt] y &= \sin(at+b) \end{align*}$

for some values of $a$ and $b.$ Observe the graph as you type each of the following Lissajous plot inputs, with $0 \leq t \leq 100.$

$\begin{align*} &\left( \sin(t), \sin(t+1) \right) \\[10pt] &\left( \sin(t), \sin(t+2) \right) \\[10pt] &\left( \sin(t), \sin(t+3) \right) \\[10pt] &\left( \sin(t), \sin(2t+1) \right) \\[10pt] &\left( \sin(t), \sin(3t+1) \right) \\[10pt] &\left( \sin(t), \sin(4t+1) \right) \\[10pt] &\left( \sin(t), \sin(5t+1) \right) \\[10pt] &\left( \sin(t), \sin(1.1t+1) \right) \\[10pt] &\left( \sin(t), \sin(1.2t+1) \right) \\[10pt] &\left( \sin(t), \sin(1.3t+1) \right) \\[10pt] &\left( \sin(t), \sin(1.4t+1) \right) \\[10pt] &\left( \sin(t), \sin(1.5t+1) \right) \end{align*}$

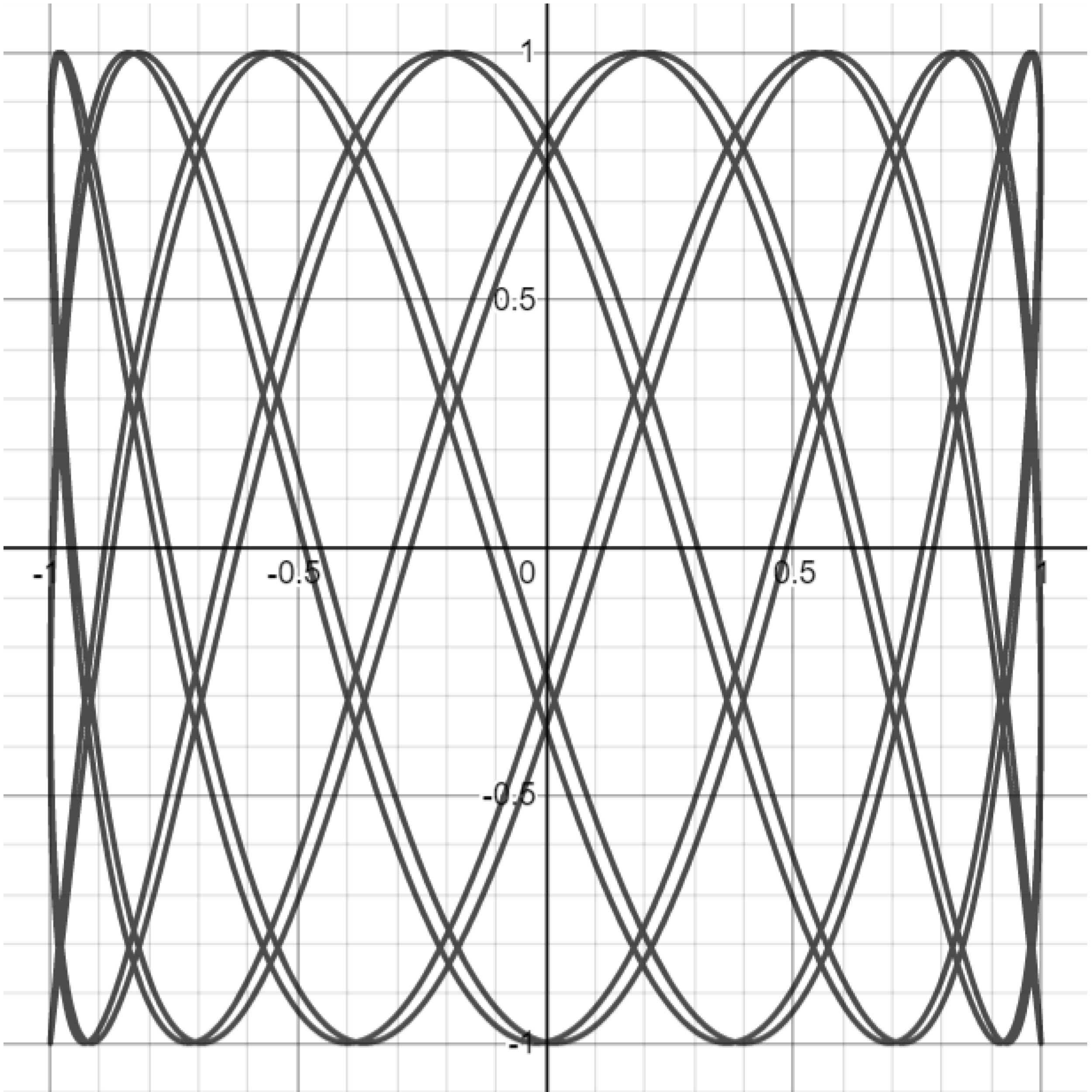
Exercise. Attempt to reproduce the graphs below by setting $a=1$ and varying the $b$ parameter in the Lissajous curve equations. You may have to play with the parameter a bit to get a sense of what it controls.

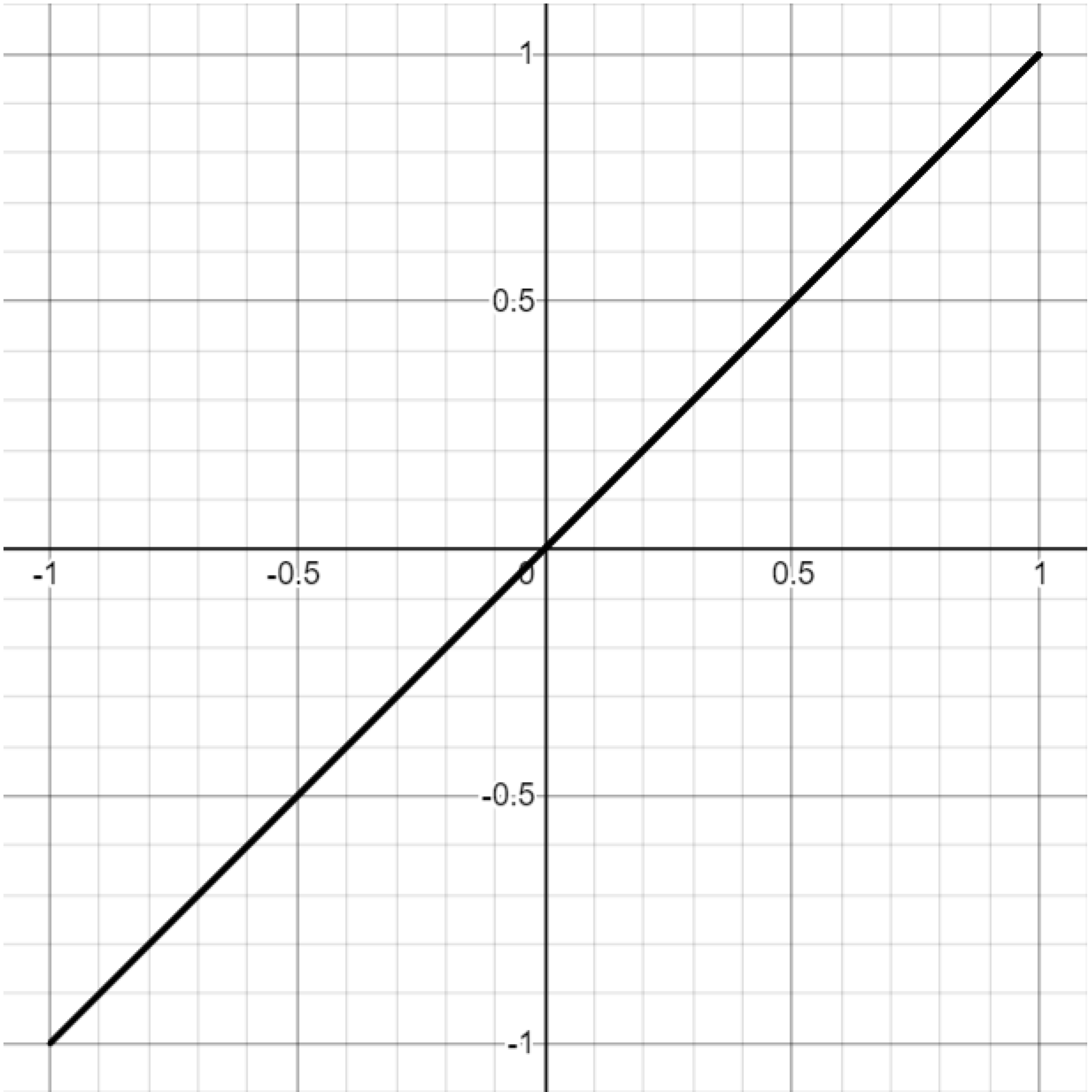
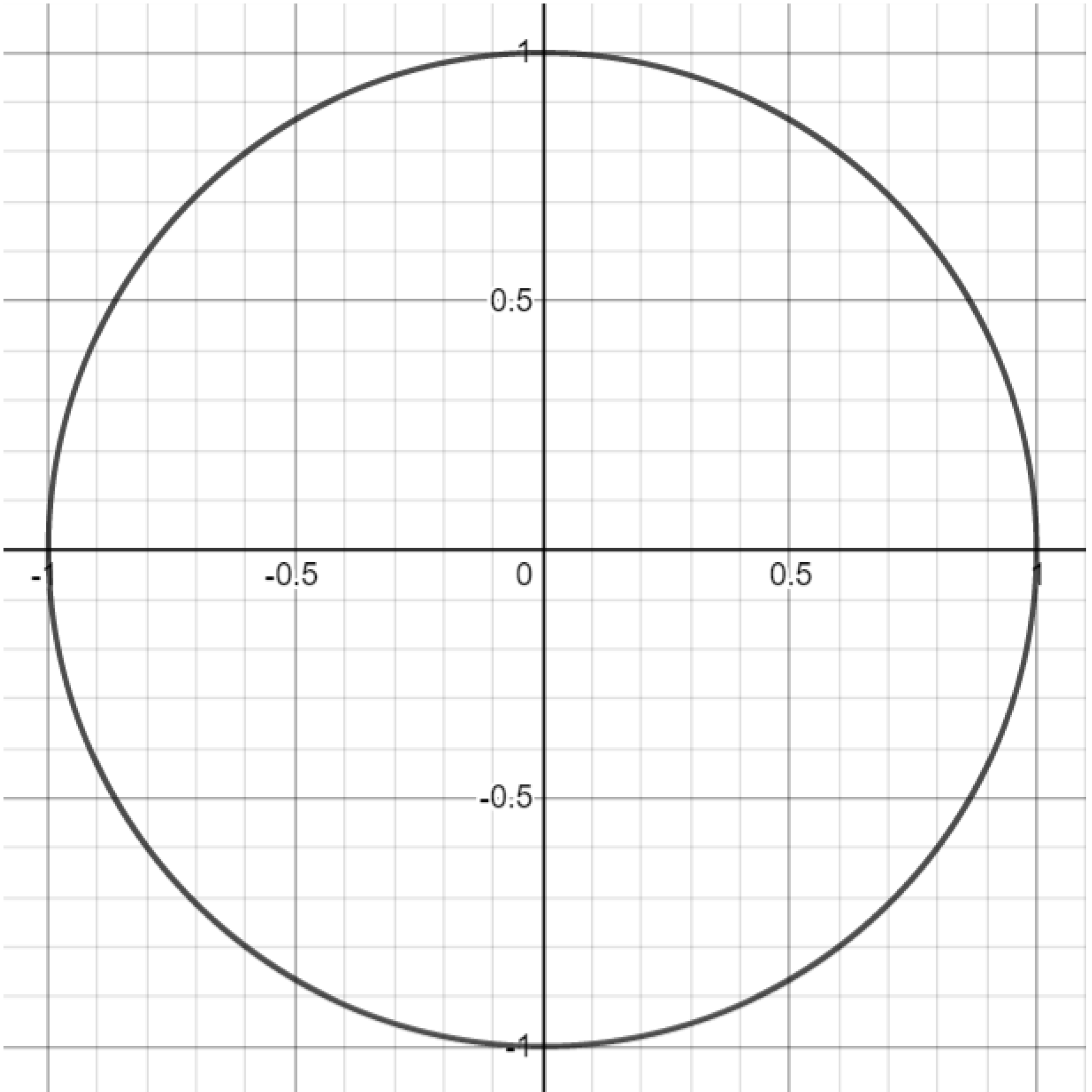
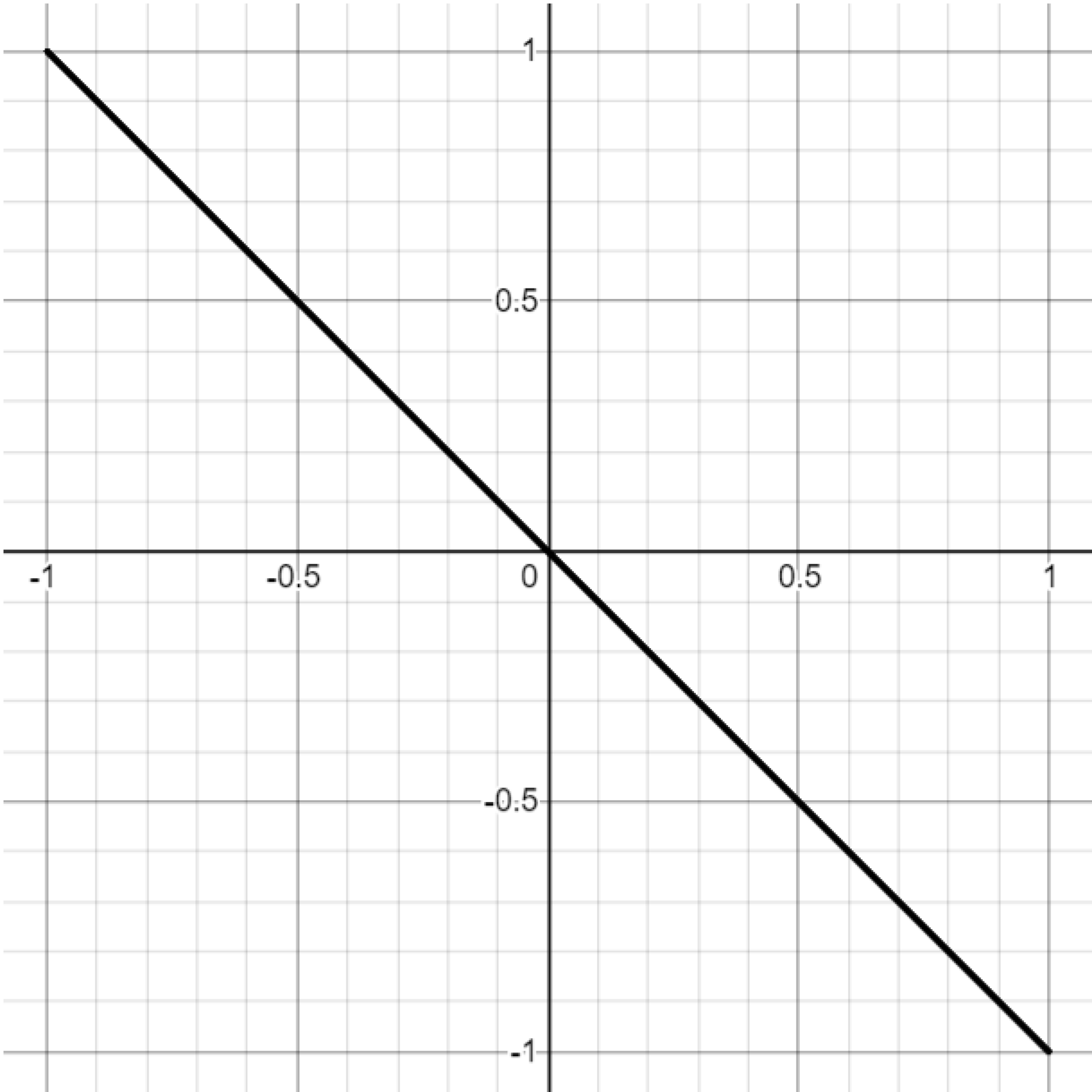
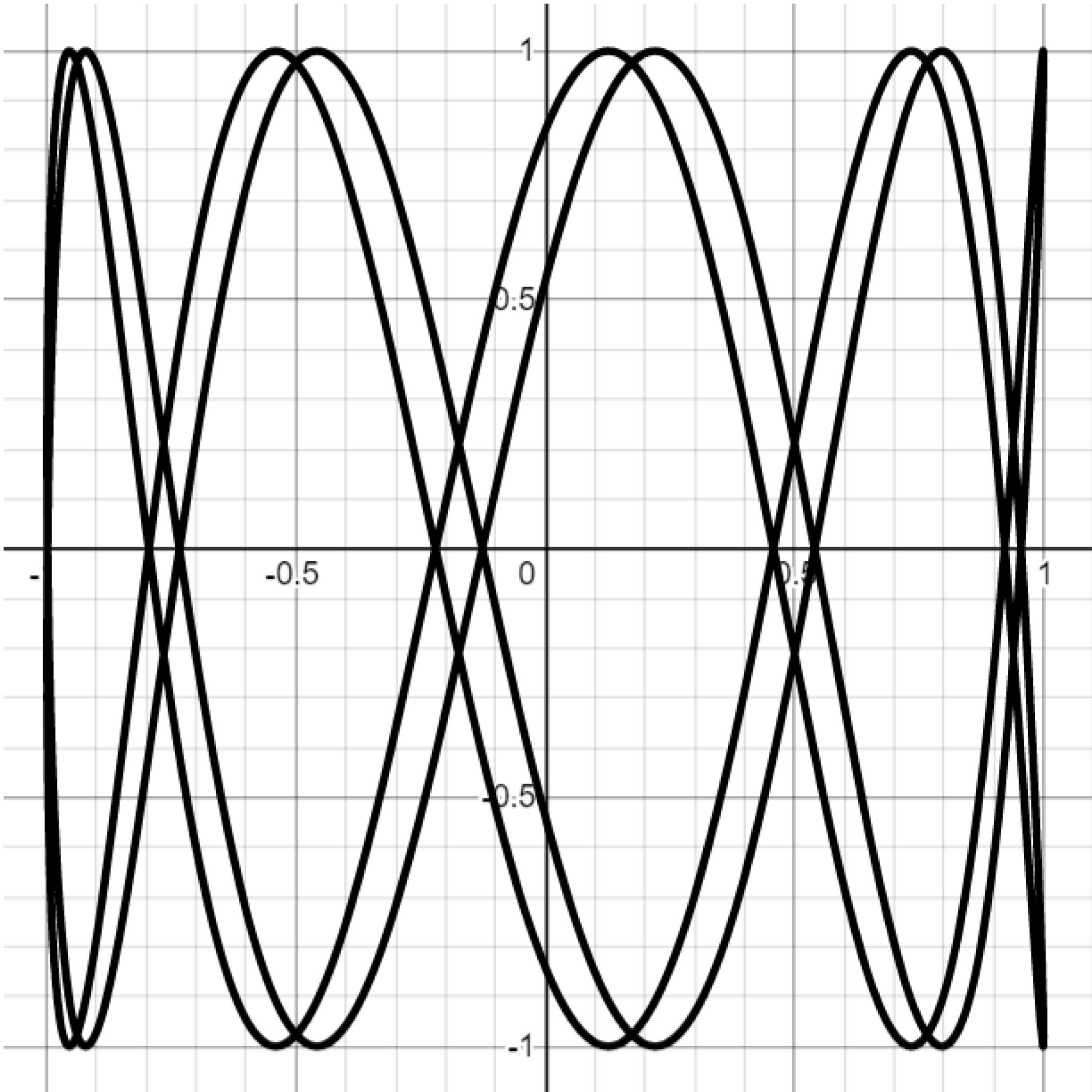
Exercise. Attempt to reproduce the graphs below by setting $b=\frac{\pi}{2}$ and varying the $a$ parameter in the Lissajous curve equations. You may have to play with the parameter a bit to get a sense of what it controls.

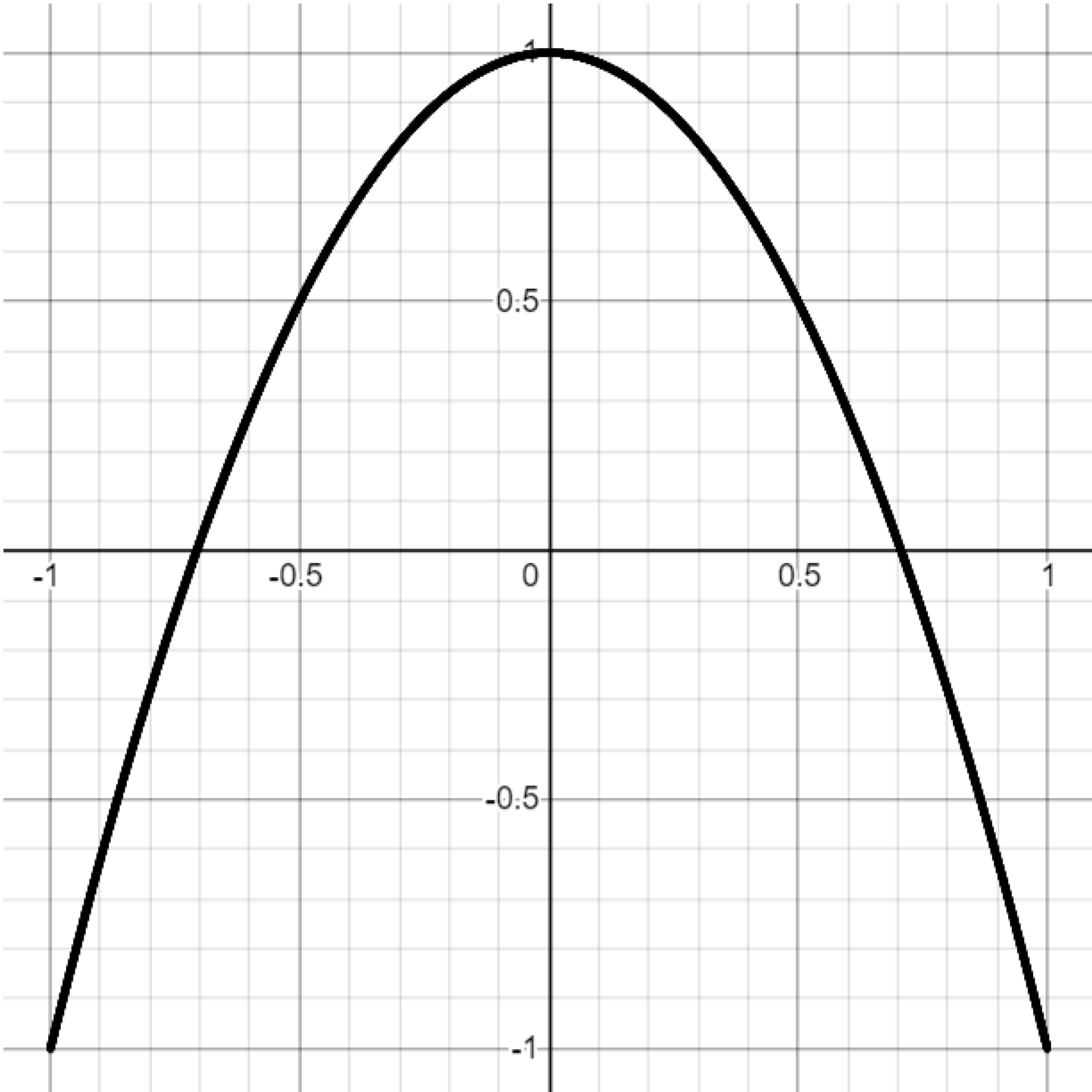
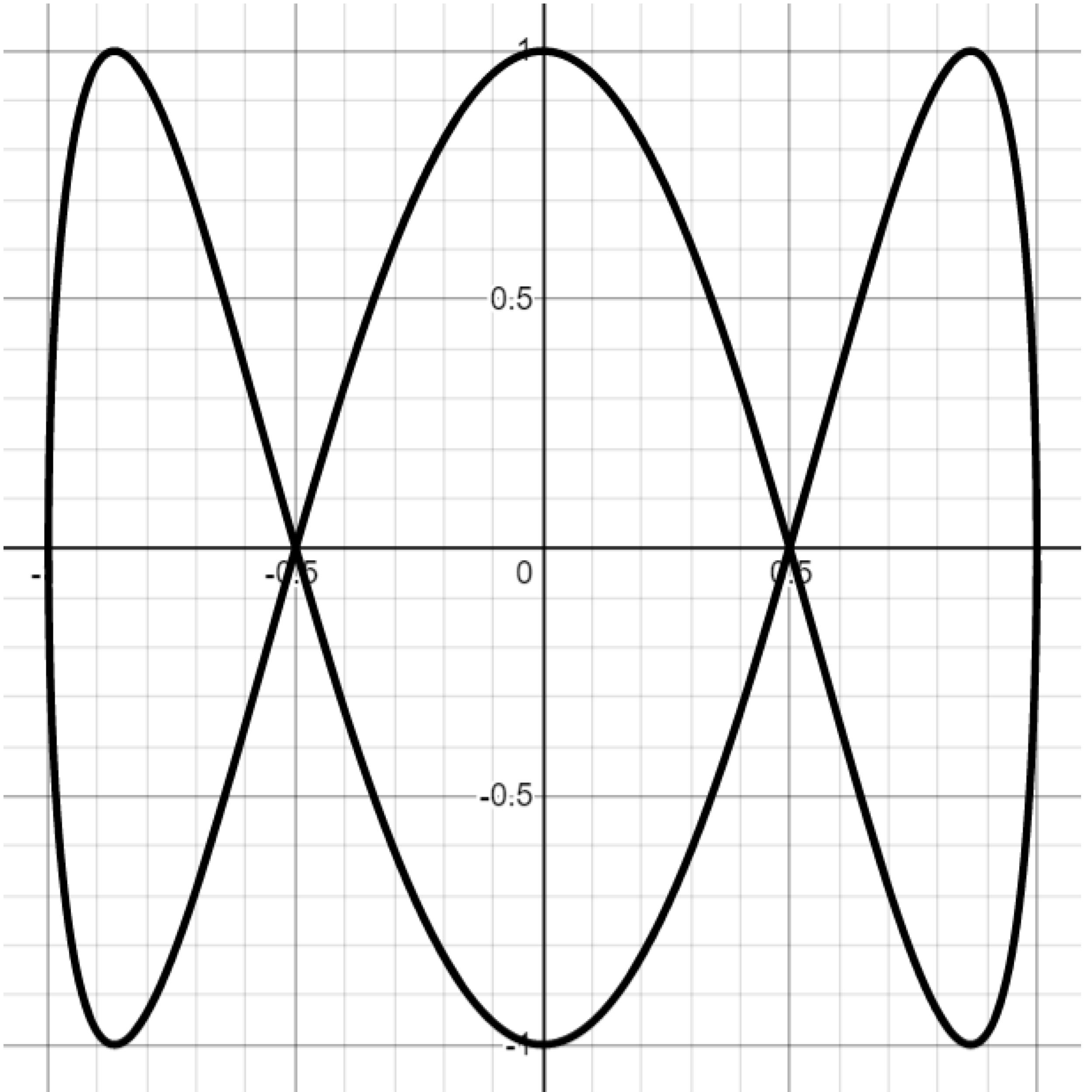
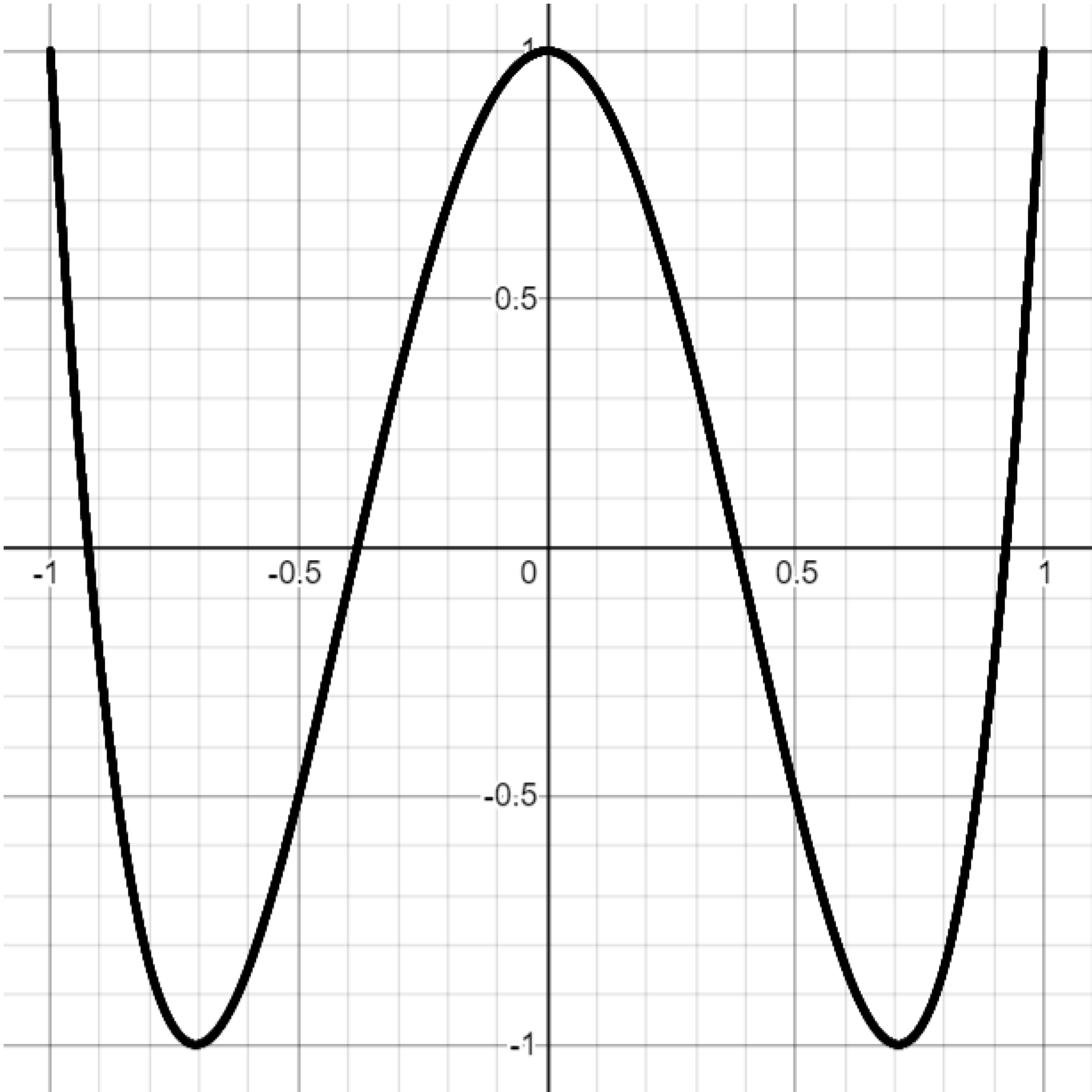
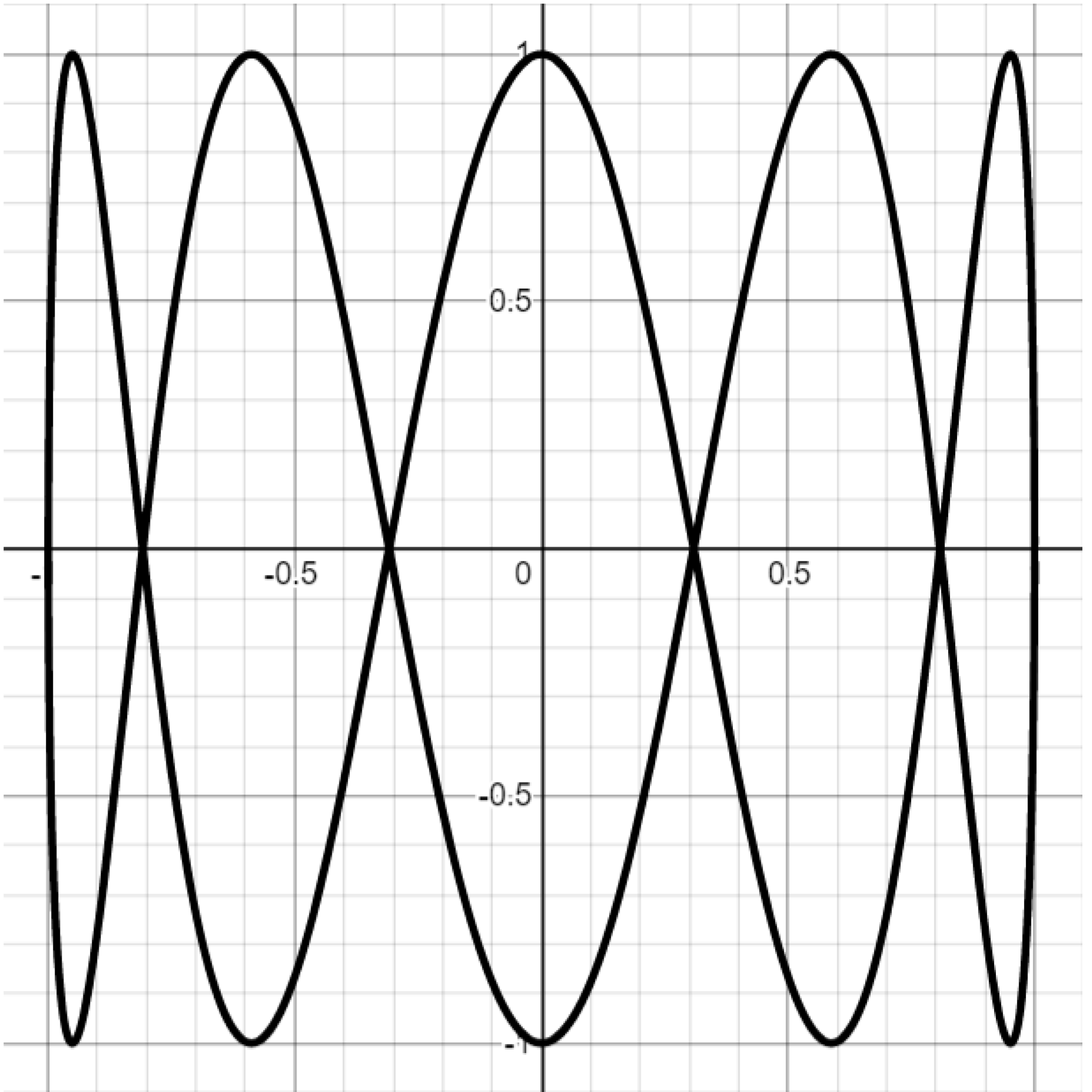
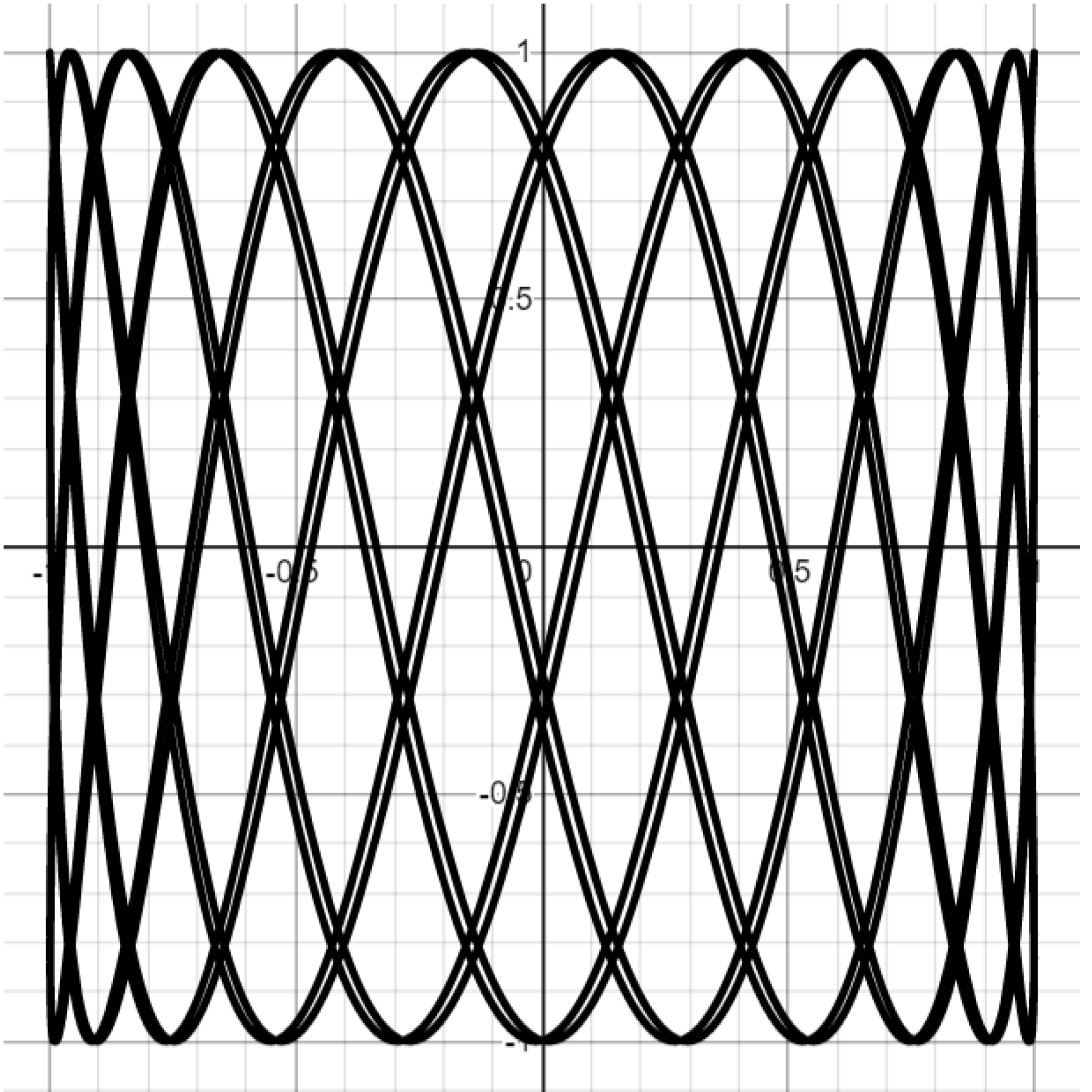
Challenge. Attempt to reproduce the Lissajous graphs below by setting $b=1$ and varying $a.$

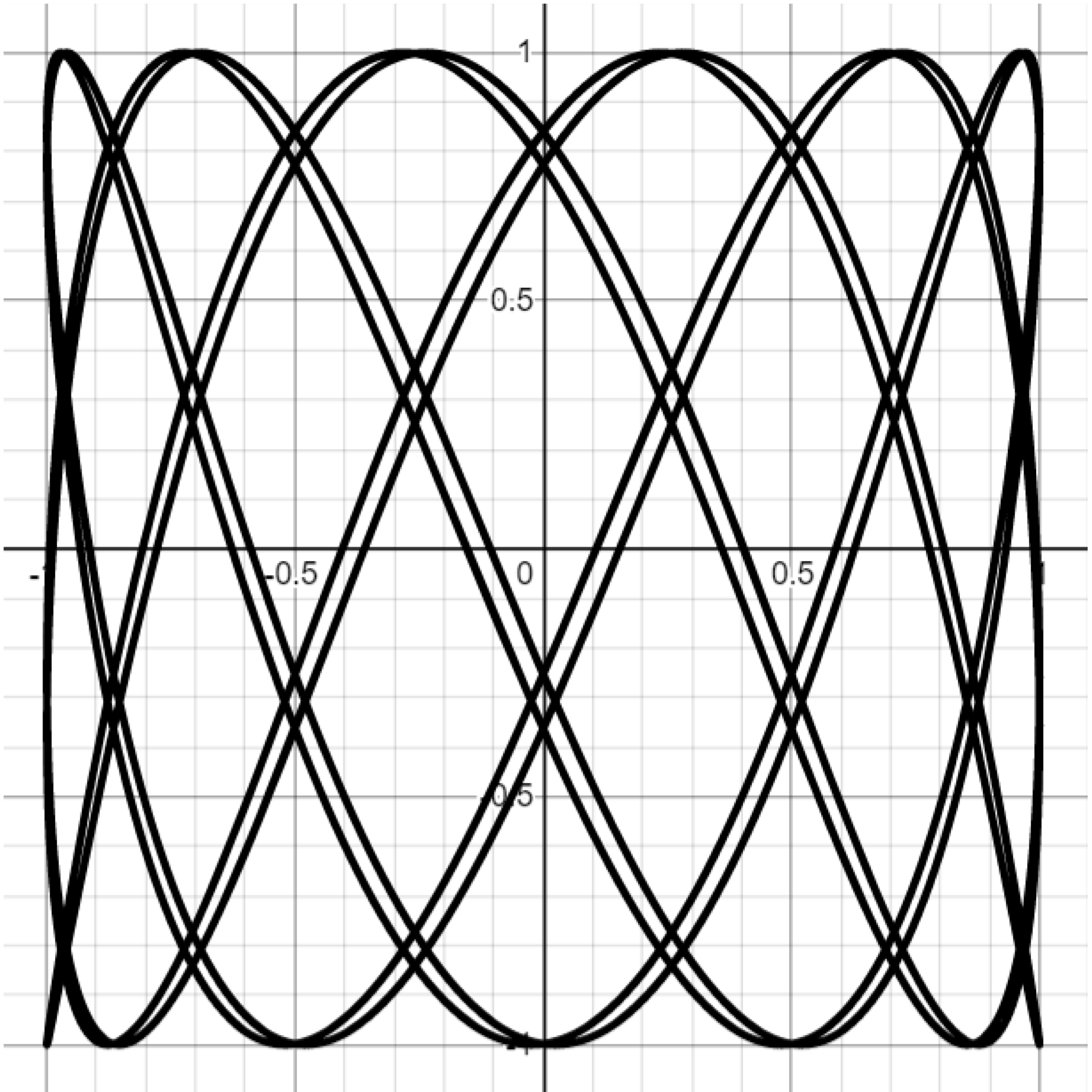
This post is part of a series.