Graphing Calculator Drawing: Euclidean Ellipses

by Justin Skycak (@justinskycak) on

Euclidean ellipses can be combined with sine wave shading to form three-dimensional shells.

This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Euclidean Ellipses. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-euclidean-ellipses/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Setup. Navigate to https://www.desmos.com/calculator. Be sure to sign in so that you can save your graph.

Demonstration - Circles. Observe the graph as you type each of the following inputs. In general, the graph of $(x-a)^2+(y-b)^2=r^2$ makes a circle with radius $r$ centered at the point $(a,b).$

$\begin{align*} &(x-0)^2+(y-0)^2=1^2 \\[10pt] &(x-2)^2+(y-3)^2 = 2^2 \\[10pt] &(x+5)^2+(y-2)^2=3^2 \end{align*}$


Demonstration - Ellipses. Observe the graph as you type each of the following inputs. In general, the graph of $\left( \frac{x-a}{A} \right)^2 + \left( \frac{y-b}{B} \right)^2 = 1$ makes an ellipse with horizontal radius \(A\) and vertical radius $B$ centered at the point $(a,b).$

$\begin{align*} &\left( \frac{x-0}{1} \right)^2 + \left( \frac{y-0}{2} \right)^2 = 1 \\[10pt] &\left( \frac{x-2}{2} \right)^2 + \left( \frac{y-3}{5} \right)^2 = 1 \end{align*}$


Demonstration - Shading. Observe the graph as you type each of the following inputs. In general, for large $v,$ the graph of $\left( \frac{x-a}{A} \right)^2 + \left( \frac{y+A\sin(vx)-b}{B} \right)^2 = 1$ shades vertically around the graph of $\left( \frac{x-a}{A} \right)^2 + \left( \frac{y-b}{B} \right)^2 = 1$ with thickness $2A.$

$\begin{align*} &\left( \frac{x-0}{1} \right)^2 + \left( \frac{y+0.1\sin(1000x)-0}{2} \right)^2 = 1 \\[10pt] &\left( \frac{x-2}{2} \right)^2 + \left( \frac{y+0.4\sin(1000x)-3}{5} \right)^2 = 1 \end{align*}$


Exercise. Use an absolute value function together with an ellipse to draw a cone.

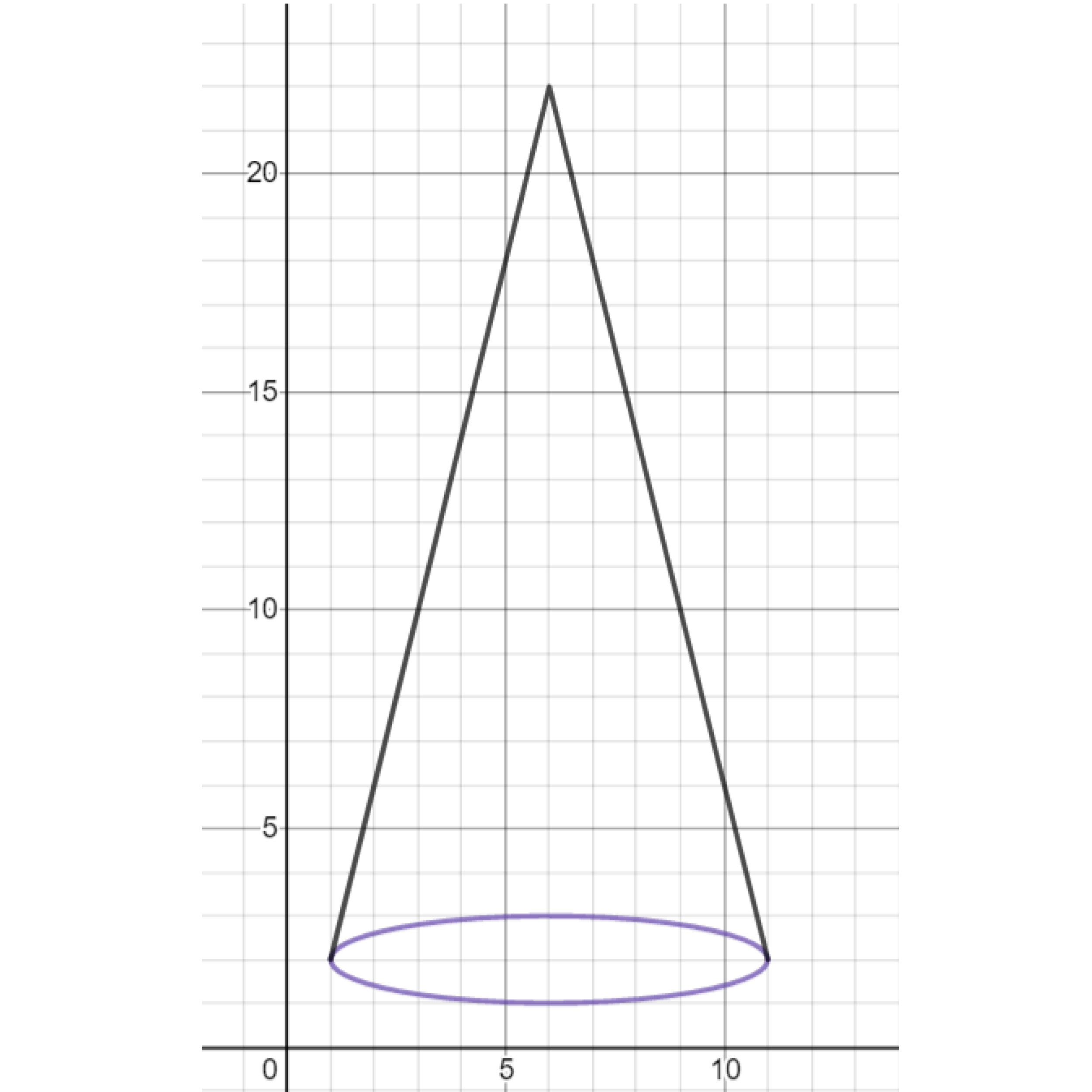
image


Exercise. Stack ellipses vertically on the cone.

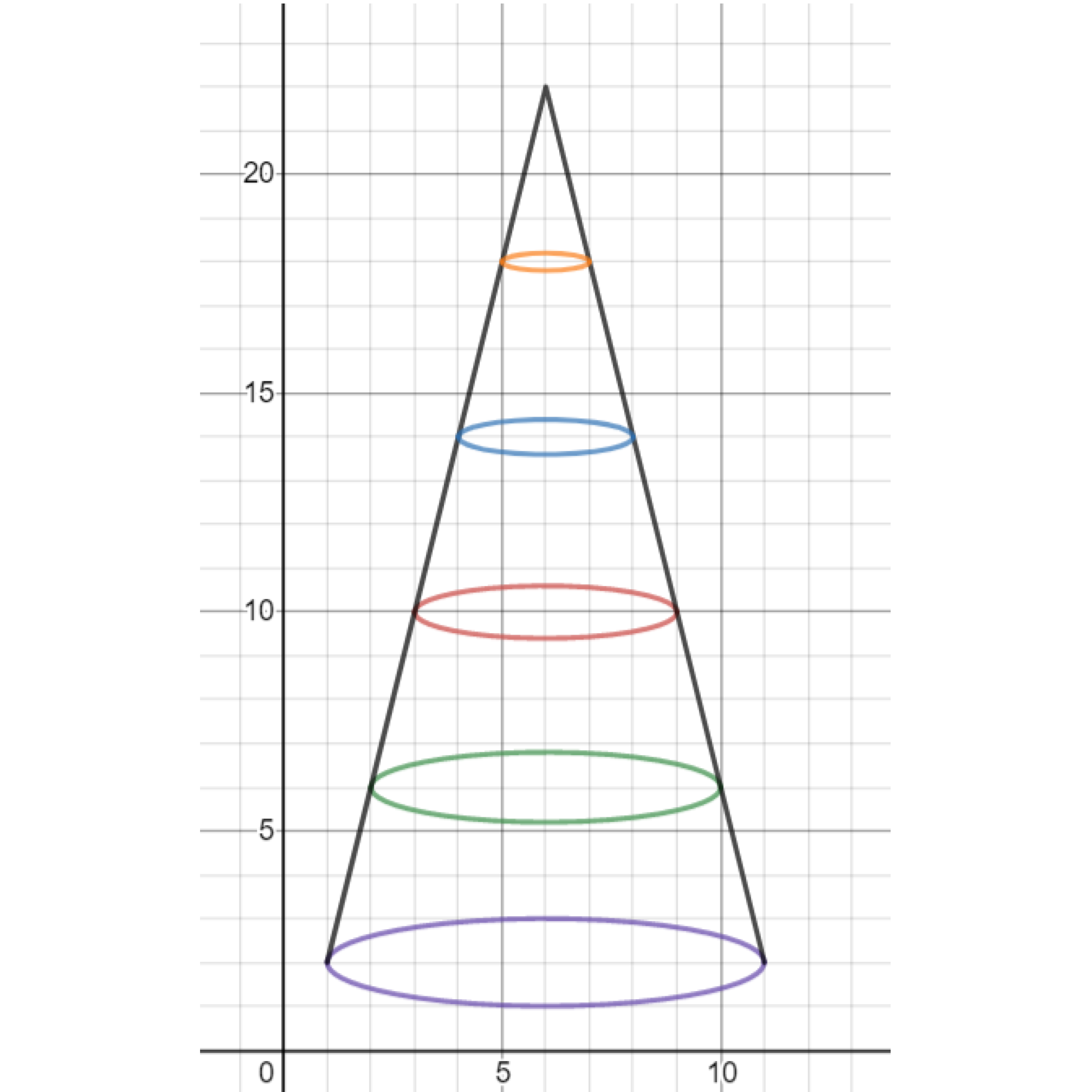
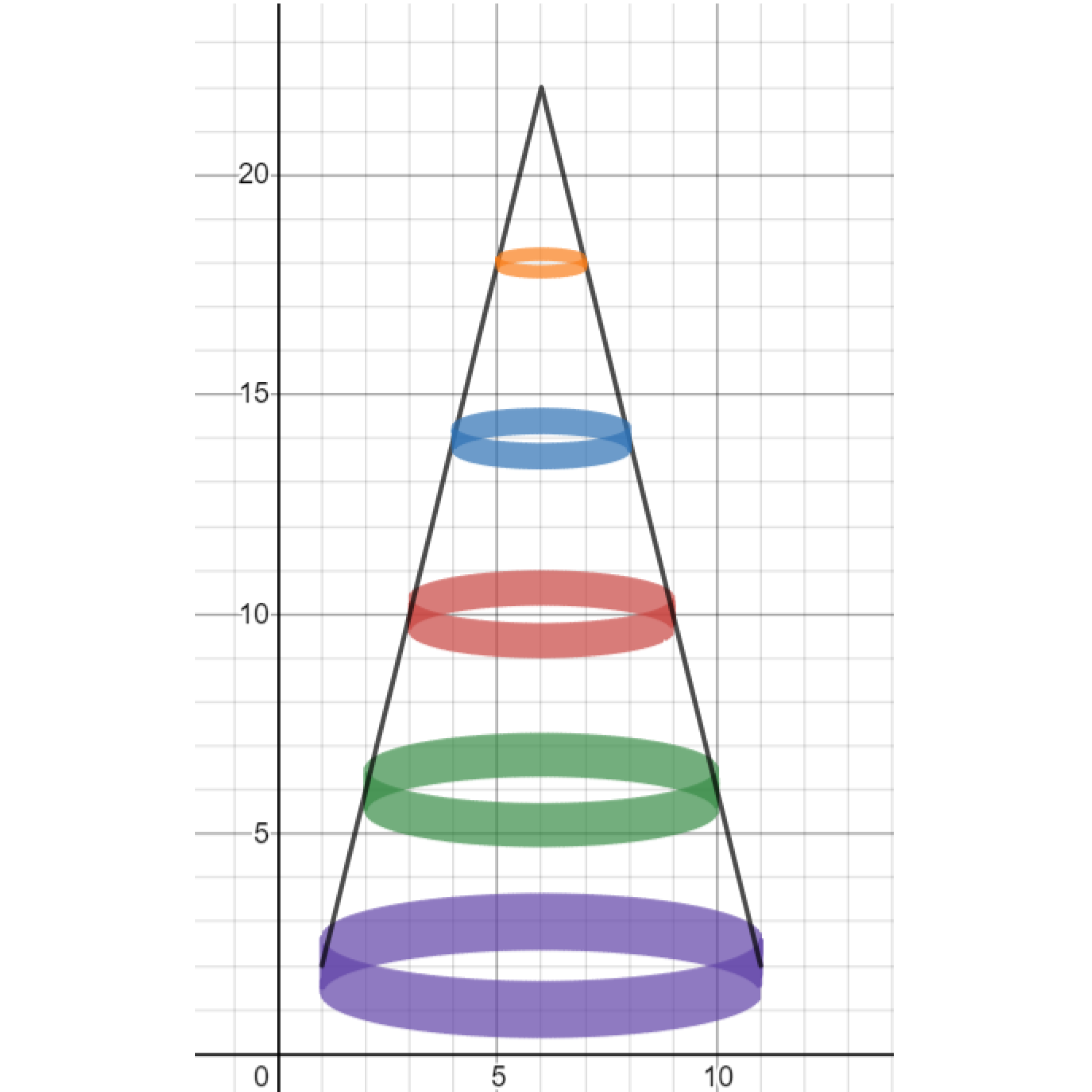
image


Exercise. Thicken the ellipses to form cylindrical shells.

image


Challenge. Try stacking cylindrical shells on the peaks of $y=\sin x.$

This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Euclidean Ellipses. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-euclidean-ellipses/


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.