Graphing Calculator Drawing: Absolute Value

by Justin Skycak (@justinskycak) on May 03, 2019

Absolute value can be used to draw a person.

This post is part of the book Graphing Calculator Drawing Exercises. Suggested citation: Skycak, J. (2019). Graphing Calculator Drawing: Absolute Value. In Graphing Calculator Drawing Exercises. https://justinmath.com/graphing-calculator-drawing-absolute-value/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Setup. Navigate to https://www.desmos.com/calculator. Be sure to sign in so that you can save your graph.

Demonstration - Absolute Value. Observe the graph as you type each of the following inputs. In general, an absolute value graph $y=m \vert x \vert$ makes a “V” shape, with the magnitude of $m$ controlling the slope of the V, and the sign of $m$ controlling whether the V opens upward or downward.

$\begin{align*} y&=5|x| \\[10pt] y&=1|x| \\[10pt] y&=0.1|x| \\[10pt] y&=-0.1|x| \\[10pt] y&=-1|x| \\[10pt] y&=-5|x| \end{align*}$

Demonstration - Shifts. Observe the graph as you type each of the following inputs. In general, the graph of $y=m \vert x-a \vert +b$ shifts the absolute value graph $y=m \vert x \vert$ so that the pointy part of the “V” occurs at the point $(a,b).$

$\begin{align*} y&=|x-1|+2 \\[10pt] y&=-2|x-1|-3 \\[10pt] y&=-0.5|x+3|-1 \\[10pt] y&=10|x+2|+1 \end{align*}$

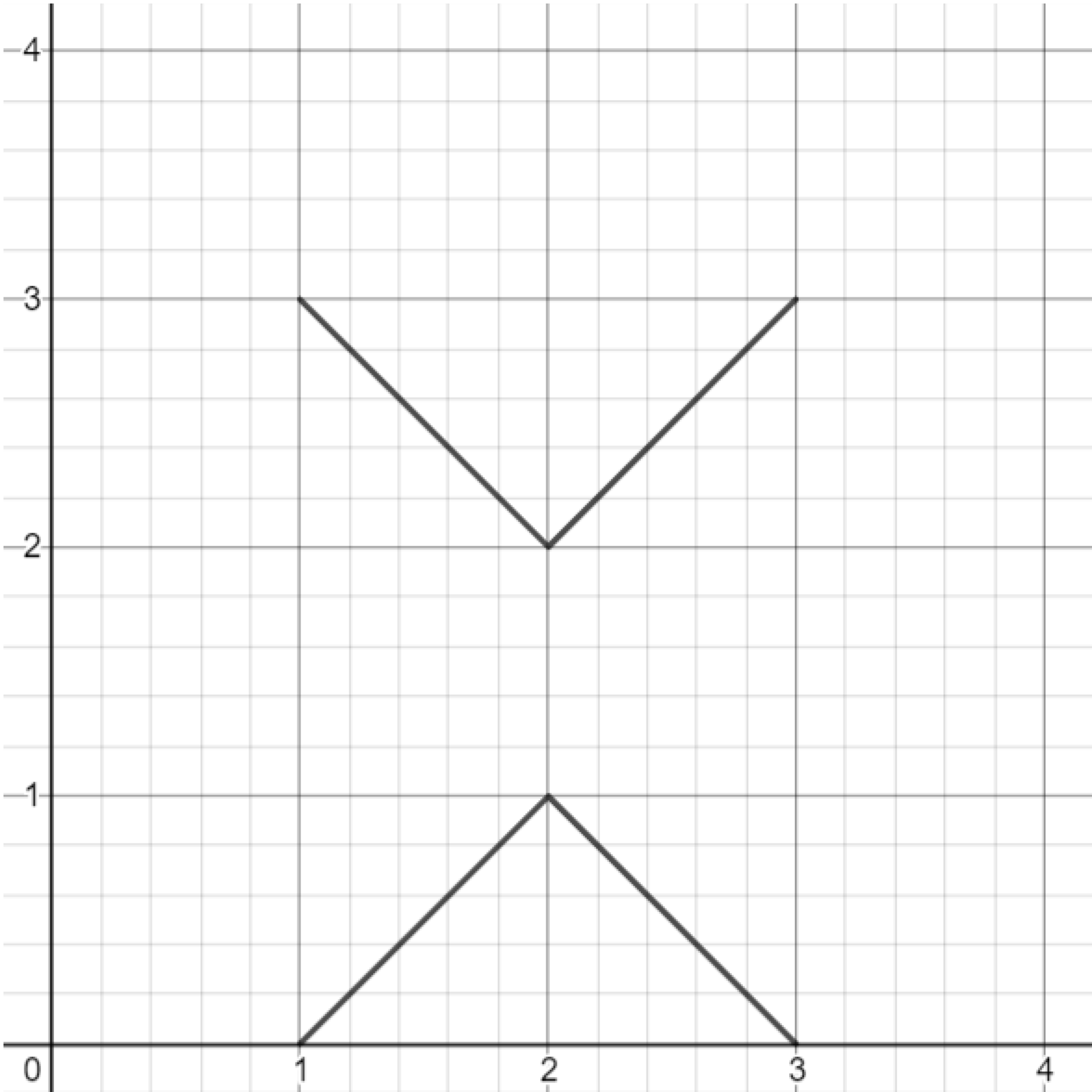
Exercise. Draw the two absolute value functions shown below. (Hint: Remember that you can limit the domain and range of your functions with parentheses, e.g. $y= \vert x \vert \lbrace -1 < x < 1 \rbrace$ or $y=\vert x \vert \lbrace y < 3 \rbrace.$)

Exercise. Draw more absolute value functions to create a person! (The person’s back will be a vertical line, but everything else can be made out of absolute value functions.)

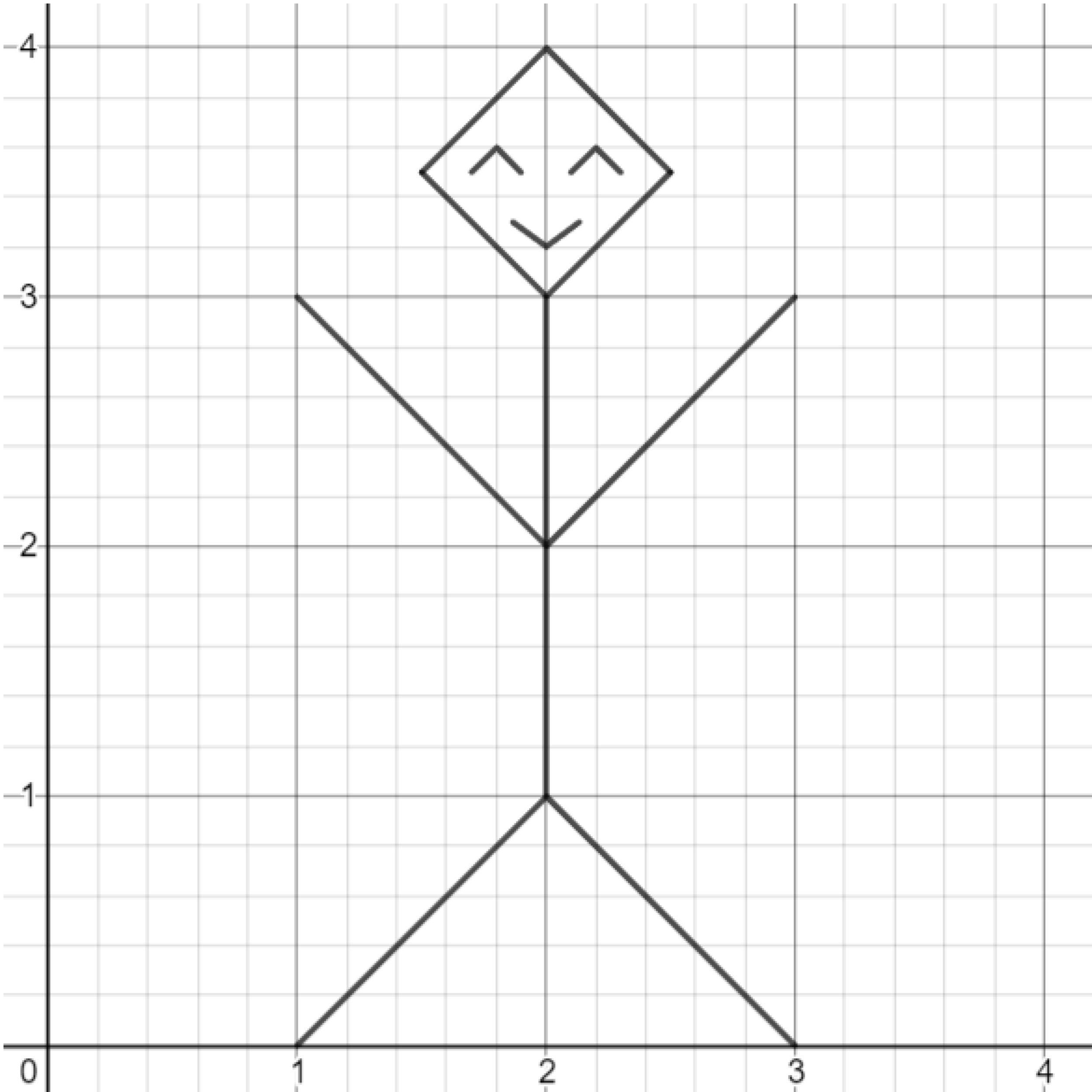
Challenge. Try to draw yourself, or your friend! You can include hair, shoes, ears, hands, clothes, etc.)

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.