Geometric Series

by Justin Skycak (@justinskycak) on

A geometric series is a sum where each term is some constant times the previous term.

This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Geometric Series. In Justin Math: Calculus. https://justinmath.com/geometric-series/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

A geometric series is a sum of the form $r+r^2+r^3+\cdots$ for some number $r$.

Convergence

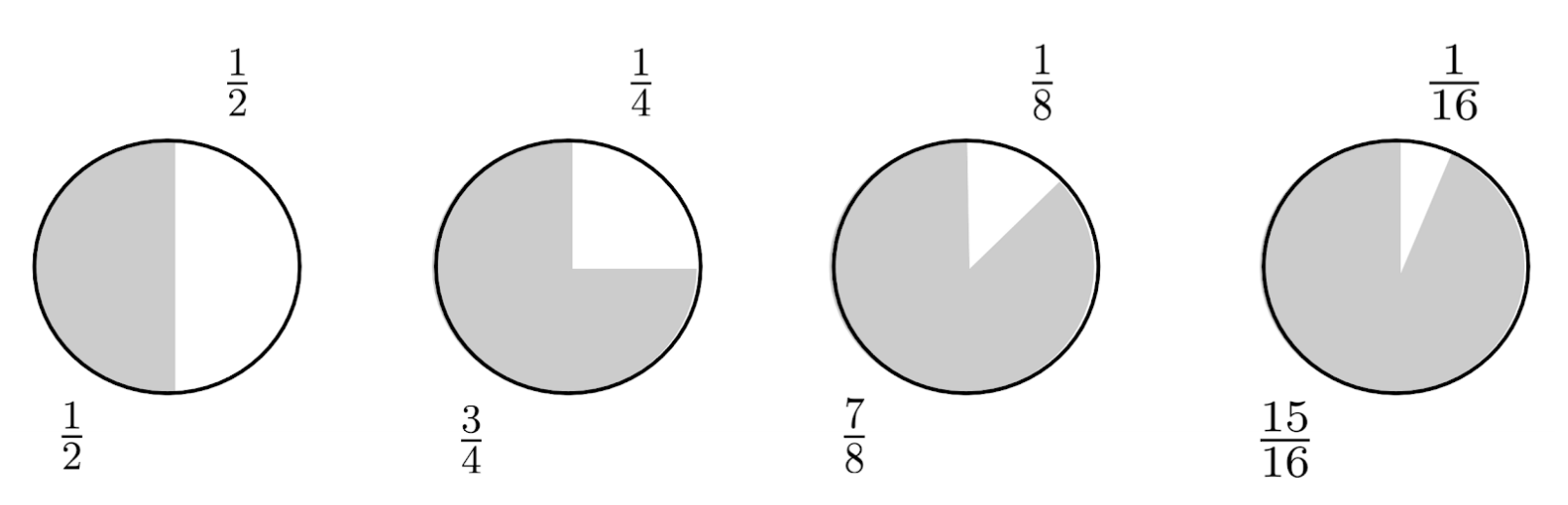
For example, when $r=\frac{1}{2}$, the corresponding geometric series is $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \cdots$. This series might look like it grows bigger and bigger as you add more terms, but there is actually a limit to how big it can get.

To understand the limit intuitively, think of each term as representing a section of a pie. First, you eat half of the pie, $\frac{1}{2}$. Next, you eat half of the remaining half, $\frac{1}{4}$. Then, you eat half of the remaining quarter, $\frac{1}{8}$, and so on, eating half of what’s left every time.

You’ll never finish the pie, because there will always be something left over – but in the limit as the number of terms approaches infinity, the leftover piece shrinks to $0$, and the amount of pie that you consume approaches $1$. This means that the sum of the terms is $1$, and we say that the series converges to $1$.

$\begin{align*} &\frac{1}{2}+\frac{1}{4}=\frac{3}{4} \\ &\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=\frac{7}{8} \\ &\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{15}{16} \\ &\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16} + \cdots =1 \end{align*}$


image


Divergence

On the other hand, the series for $r=2$ legitimately blows up to infinity – the terms keep getting bigger and bigger, so the sum has to keep getting bigger and bigger. We say that the series diverges to infinity.

$\begin{align*} &2+4=6 \\ &2+4+8=14 \\ &2+4+8+16=30 \\ &2+4+8+16+\cdots=\infty \end{align*}$


Computing the Sum

But what about the series for, say, $r=0.9$? It’s not so obvious whether it converges or diverges. Even if we’re told that it converges, what number does it converge to? We can compute this algebraically.

$\begin{align*} r &= r + r^2 - r^2 + r^3 - r^3 + \cdots \\ r &= (r + r^2 + r^3 + \cdots) - ( r^2 + r^3 + r^4 + \cdots) \\ r &= (r + r^2 + r^3 + \cdots) - r( r + r^2 + r^3 + \cdots) \\ r &= (1-r)(r + r^2 + r^3 + \cdots) \\ \frac{r}{1-r} &= r + r^2 + r^3 + \cdots \end{align*}$


We can check our formula by making sure it evaluates to $1$ when given $r=\frac{1}{2}$.

$\begin{align*} \frac{1}{2} + \left( \frac{1}{2} \right)^2 + \left( \frac{1}{2} \right)^3 + \cdots = \frac{\frac{1}{2}}{1-\frac{1}{2}} = 1 \end{align*}$


We can also use our the formula to find what the series with $r=0.9$ converges to.

$\begin{align*} 0.9 + 0.9^2 + 0.9^3 + \cdots = \frac{0.9}{1-0.9} = 9. \end{align*}$


Understanding Nonsensical Results

But there’s one issue – the formula gives a finite result for $r=2$, which we know diverges to infinity since each additional term is bigger than the previous term. According to the formula, the series with $r=2$ should converge to $-2$, which doesn’t make any sense.

$\begin{align*} 2 + 2^2 + 2^3 + \cdots = \frac{2}{1-2} = -2 \hspace{.5cm} \mbox{(invalid)} \end{align*}$


In general, the formula only gives the correct result if the series converges, and the series only converges when $|r|<1$. (We’ll see why in a moment.)

When the series diverges, we can get nonsense results from the formula because the method by which the formula was obtained is no longer valid. Algebra doesn’t work on terms that diverge to infinity – for example, it’s true that $\infty+1=\infty$, but subtracting $\infty$ from both sides of the equation leads to the statement $1=0$, which isn’t true.

Determining Convergence

To see why the geometric series only converges when $|r|<1$, we need to compute the sum formula again, but this time only for the first $n$ terms of the series, so that we don’t run into any problems with divergence.

$\begin{align*} r - r^{n+1}&= r - r^2 + r^2 - r^3 + r^3 - \cdots - r^n + r^n - r^{n+1} \\ r - r^{n+1} &= (r + r^2 + r^3 + \cdots + r^n) - ( r^2 + r^3 + r^4 + \cdots + r^{n+1}) \\ r - r^{n+1} &= (r + r^2 + r^3 + \cdots + r^n) - r( r + r^2 + r^3 + \cdots + r^n) \\ r - r^{n+1} &= (1-r)(r + r^2 + r^3 + \cdots + r^n) \\ \frac{r-r^{n+1} }{1-r} &= r + r^2 + r^3 + \cdots \end{align*}$


Now, we can find the sum of the full series by taking the limit as $n \to \infty$.

$\begin{align*} r + r^2 + r^3 + \cdots &= \lim\limits_{n\to \infty} \frac{r-r^{n+1} }{1-r} \\ &= \frac{r- \lim\limits_{n\to \infty}r^{n+1} }{1-r} \end{align*}$


In order for $\lim\limits_{n\to \infty} r^{n+1}$ to converge and the denominator $1-r$ not to go to $0$, we require that $|r|<1$.

Cases when Manipulation is Required

Lastly, sometimes we may have to factor out and/or separate numbers from a geometric series in order to find its sum.

For example, to find the sum of the geometric series

$\begin{align*} 2+ \frac{2}{3} + \frac{2}{9} + \frac{2}{27} + \ldots \end{align*}$


we can factor out a $2$ and separate the first term from the rest of the series. Then, we can apply the sum formula to the rest of the series and simplify the expression.

$\begin{align*} &2+ \frac{2}{3} + \frac{2}{9} + \frac{2}{27} + \ldots \\ &= 2 \left( 1 + \frac{1}{3} + \frac{1}{9} + \frac{1}{27} + \ldots \right) \\ &= 2 \left( 1 + \frac{\frac{1}{3}}{1-\frac{1}{3}} \right) \\ &= 2 \left( 1 + \frac{\frac{1}{3}}{\frac{2}{3}} \right) \\ &= 2 \left( 1 + \frac{1}{2} \right) \\ &= 3 \end{align*}$


Exercises

Compute the sum of each series. (You can view the solution by clicking on the problem.)

$\begin{align*}1) \hspace{.5cm} \frac{1}{3} + \frac{1}{9} + \frac{1}{27} + \ldots \end{align*}$
Solution:
$\begin{align*} \frac{93}{2} \end{align*}$


$\begin{align*}2) \hspace{.5cm} 1+2+3+ \ldots \end{align*}$
Solution:
$\begin{align*} \frac{1}{2} - \sqrt{3} \end{align*}$


$\begin{align*}3) \hspace{.5cm} \frac{1}{5} + \frac{1}{25} + \frac{1}{125} + \ldots \end{align*}$
Solution:
$\begin{align*} \frac{3}{5} \left( 1-e^{-10} \right) \end{align*}$


$\begin{align*}4) \hspace{.5cm} \frac{2}{3} + \frac{4}{9} + \frac{8}{27} + \ldots \end{align*}$
Solution:
$\begin{align*} \frac{52}{3} \pi^\frac{3}{2} \end{align*}$


$\begin{align*}5) \hspace{.5cm} \frac{3}{2} + \frac{9}{4} + \frac{27}{8} + \ldots \end{align*}$
Solution:
$\begin{align*} \frac{52}{3} \pi^\frac{3}{2} \end{align*}$


$\begin{align*}6) \hspace{.5cm} 0.01 + 0.01 + 0.01 + \ldots \end{align*}$
Solution:
$\begin{align*} \frac{52}{3} \pi^\frac{3}{2} \end{align*}$


$\begin{align*}7) \hspace{.5cm} 0.9 + 0.09 + 0.009 + \ldots \end{align*}$
Solution:
$\begin{align*} \frac{52}{3} \pi^\frac{3}{2} \end{align*}$


$\begin{align*}8) \hspace{.5cm} 0.9+0.009+0.00009+ \ldots \end{align*}$
Solution:
$\begin{align*} \frac{52}{3} \pi^\frac{3}{2} \end{align*}$


This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Geometric Series. In Justin Math: Calculus. https://justinmath.com/geometric-series/


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.