Exponential and Logarithmic Functions
Exponential functions have variables as exponents. Logarithms cancel out exponentiation.
This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Exponential and Logarithmic Functions. In Justin Math: Algebra. https://justinmath.com/exponential-and-logarithmic-functions/
Exponential functions have variables as exponents, e.g. $f(x)=2^x$.
Their end behavior consists of growing without bound to infinity in one direction, and decaying to a horizontal asymptote of $y=0$ in the other direction.
The size of the number that is exponentiated, called the base, governs which direction corresponds to which end behavior.
Exponential Growth
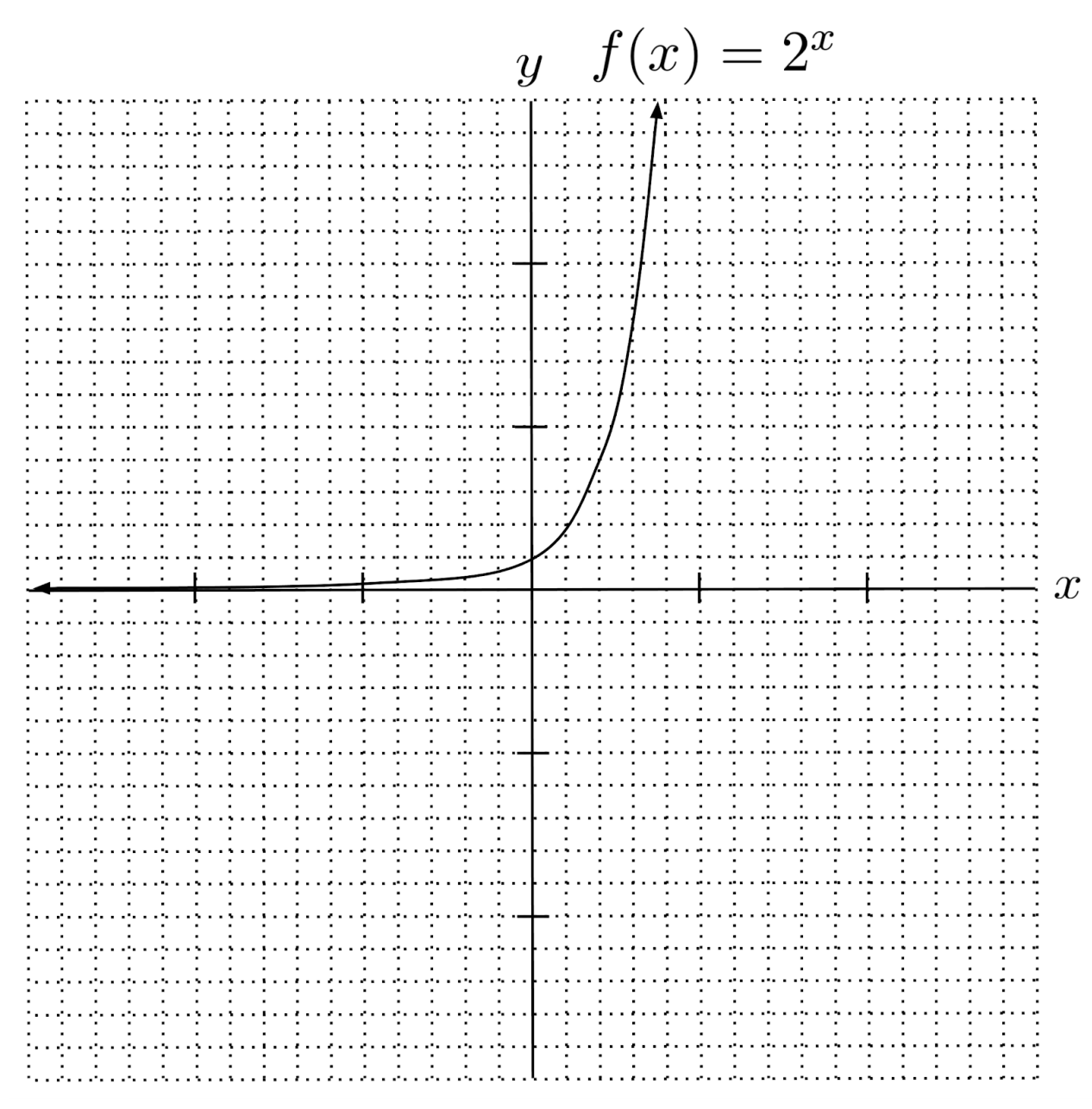
If the magnitude of the base is bigger than $1$, then as $x$ increases, the function is repeatedly multiplied by a number bigger than $1$ and consequently grows without bound to infinity. For this reason, such functions are called exponential growth functions.
By the same token, as $x$ decreases, the function is repeatedly divided by a number bigger than $1$ and consequently decays to a horizontal asymptote of $y=0$.
For example, for the exponential growth function $f(x)=x^2$, each unit increase in $x$ causes the output to be doubled, and each unit decrease in $x$ causes the output to be halved.
Exponential Decay
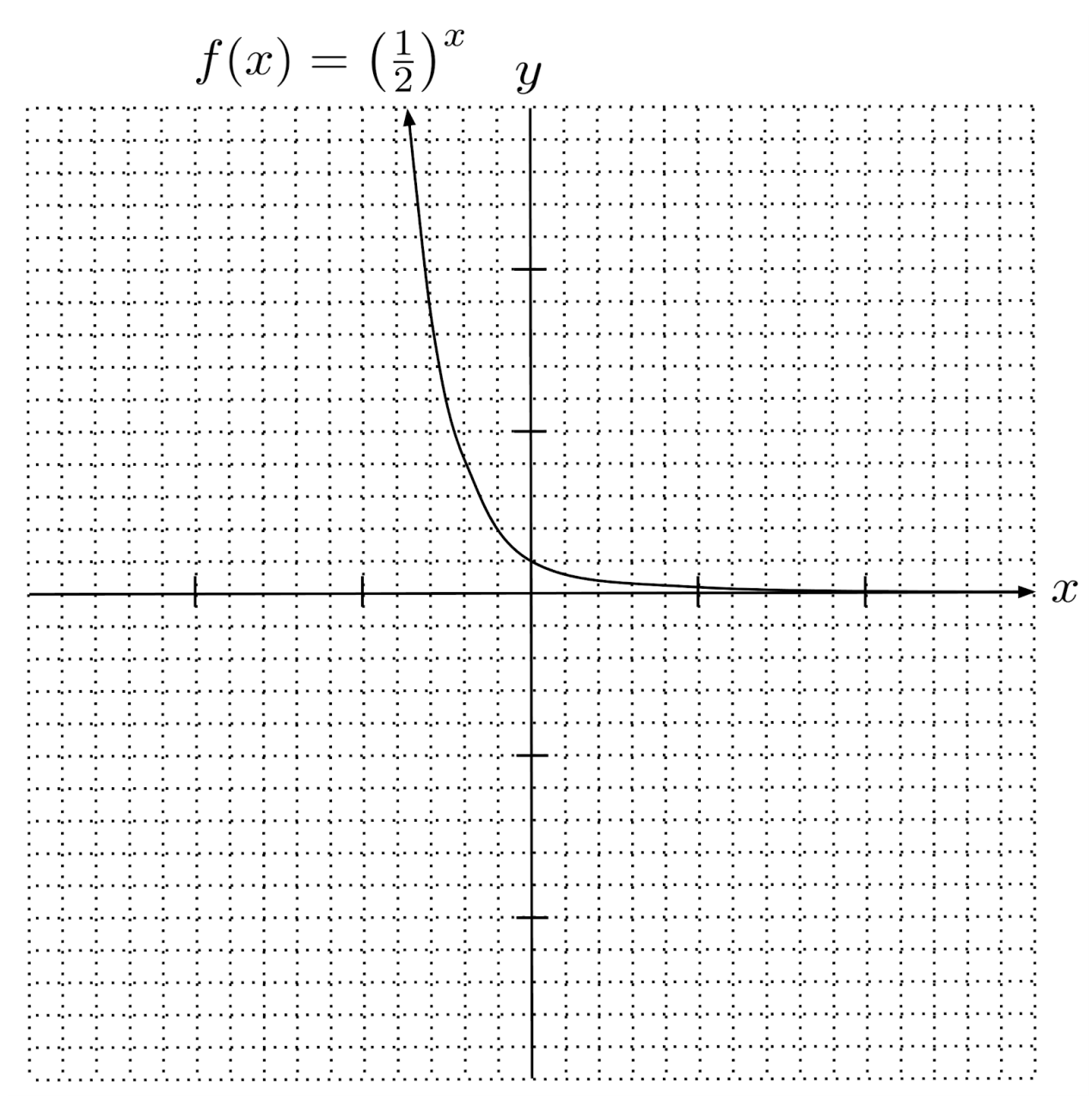
On the other hand, if the magnitude of the base is smaller than $1$, then as $x$ increases, the function is repeatedly multiplied by a number smaller than $1$ and consequently decays to a horizontal asymptote of $y=0$. For this reason, such functions are called exponential decay functions.
By the same token, as $x$ decreases, the function is repeatedly divided by a number smaller than $1$ and consequently grows without bound to infinity.
For example, for the exponential decay function $f(x) = \left( \frac{1}{2} \right)^x$, each unit increase in $x$ causes the output to be halved, and each unit decrease in $x$ causes the output to be doubled.
Logarithms
Equations involving exponential terms can be solved with the help of logarithmic functions, which cancel out exponentiation.
For example, the equation $2^x=5$ is solved by $x=\log_2 5$, the logarithm base-$2$ of $5$, which evaluates to roughly $2.32$ via calculator.
If your calculator does not allow you to input a base for a logarithm, you can compute $\log_2 5$ as $\frac{\log 5}{\log 2}$. This is called the change-of-base formula.
Logarithmic graphs look similar to square-root graphs, except they cross the x-axis at and extend downward towards an asymptote at $x=0$.
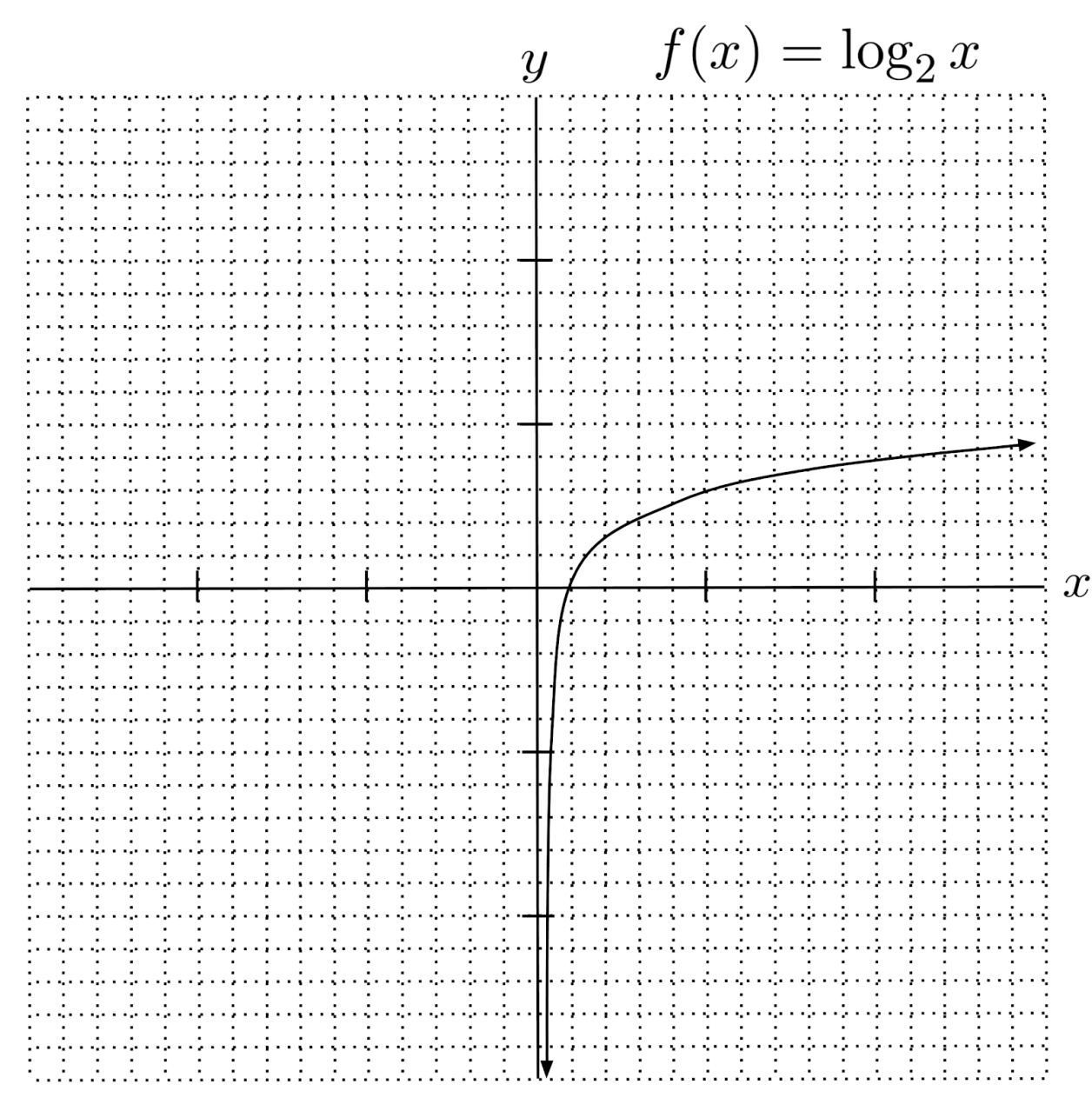
Logarithmic graphs cross the x-axis at $1$ because raising any number to the power of $0$ results in $1$. That is, any logarithm $x=\log_b 1$ solves the equation $b^x=1$, which we already know is solved by $x=0$.
Also, logarithmic graphs extend to negative infinity as $x$ approaches $0$, because a number (greater than one) gets smaller and smaller as its exponent gets more and more negative.
Lastly, the base of the logarithm tells us where the y-value is $1$ – that is, the function $f(x)=\log_b x$ has $f(b)=1$. This is because $\log_b b$ is the exponent we have to raise $b$ to, to get $b$.
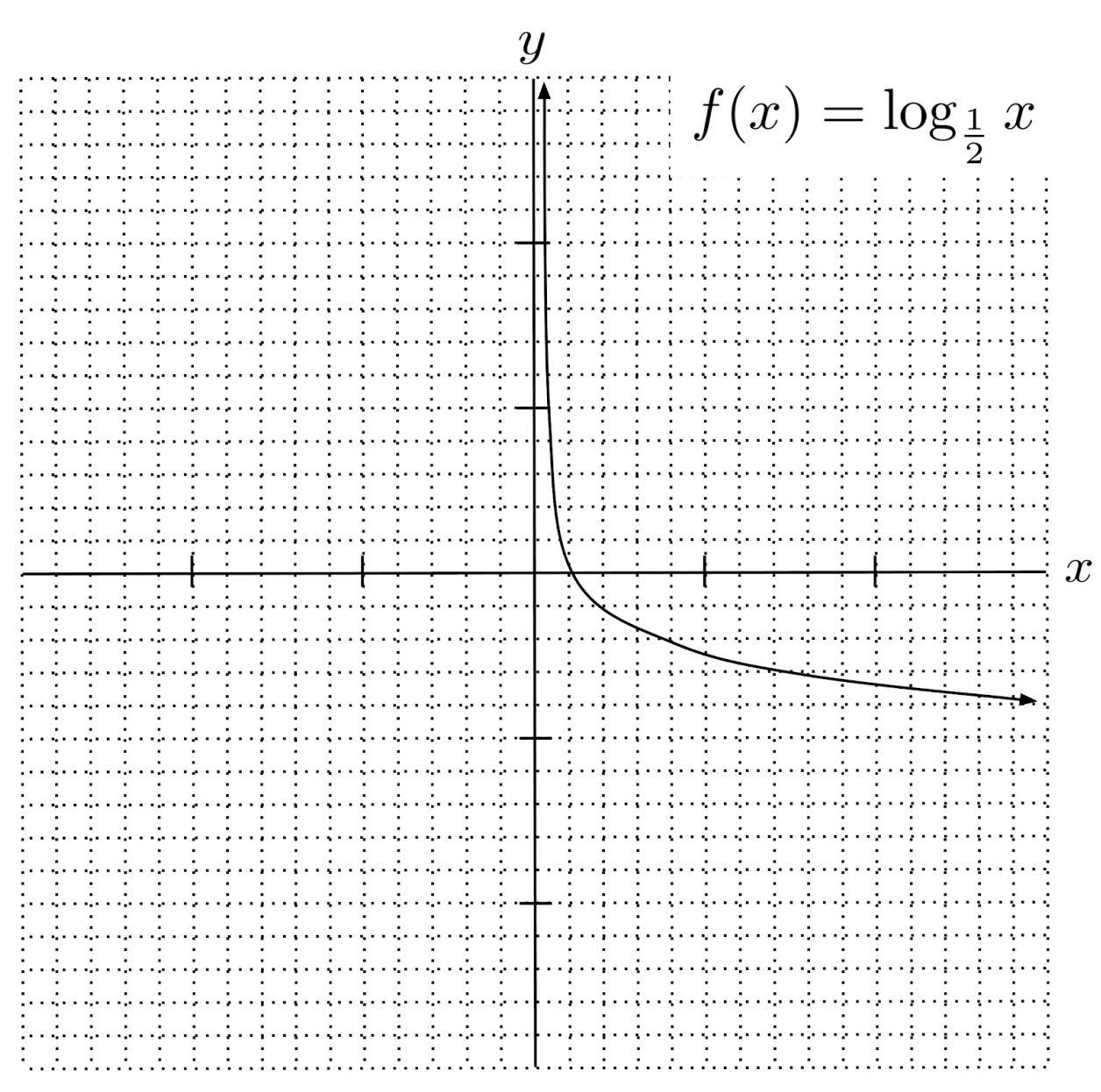
When the base of the logarithm is smaller than one, the graph flips over the x-axis.
In this case, the graph extends to positive infinity as $x$ approaches $0$, because a number smaller than $1$ gets closer and closer to $0$ as its exponent increases.
Likewise, as $x$ increases, the graph becomes more and more negative because a negative exponent is needed to flip the fractional base.
Properties of Logarithms
Expressions consisting of multiple logarithms of the same base can be simplified by using two properties of logarithms:
- Addition outside two logarithms with the same base turns into multiplication inside a single logarithm. For example, $\log_2 4 + \log_2 8 = \log_2 32$, and in general, $\log_b x + \log_b y = \log_b xy$.
- Multiplication outside two logarithms with the same base turns into exponentiation inside a single logarithm. For example, $3\log_2 4 = \log_2 4^3 = \log_2 64$, and in general, $a \log_b x = \log_b x^a$.
A particularly noteworthy consequence of the second rule is that negative outside a log turns into reciprocal inside the log:
Sometimes, logarithms of different bases can be converted to logarithms of the same base. For example, $\log_2 4$ is the same as $\log_4 16$. In general, $\log_{b^n} x^n = \log_b x$ provided both logarithms exist.
Below is an example of simplifying a logarithmic expression using all of the properties that we have discussed:
Exercises
Graph the following exponential functions. (You can view the solution by clicking on the problem.)
$1) \hspace{.5cm} f(x)=3^x$
Solution:
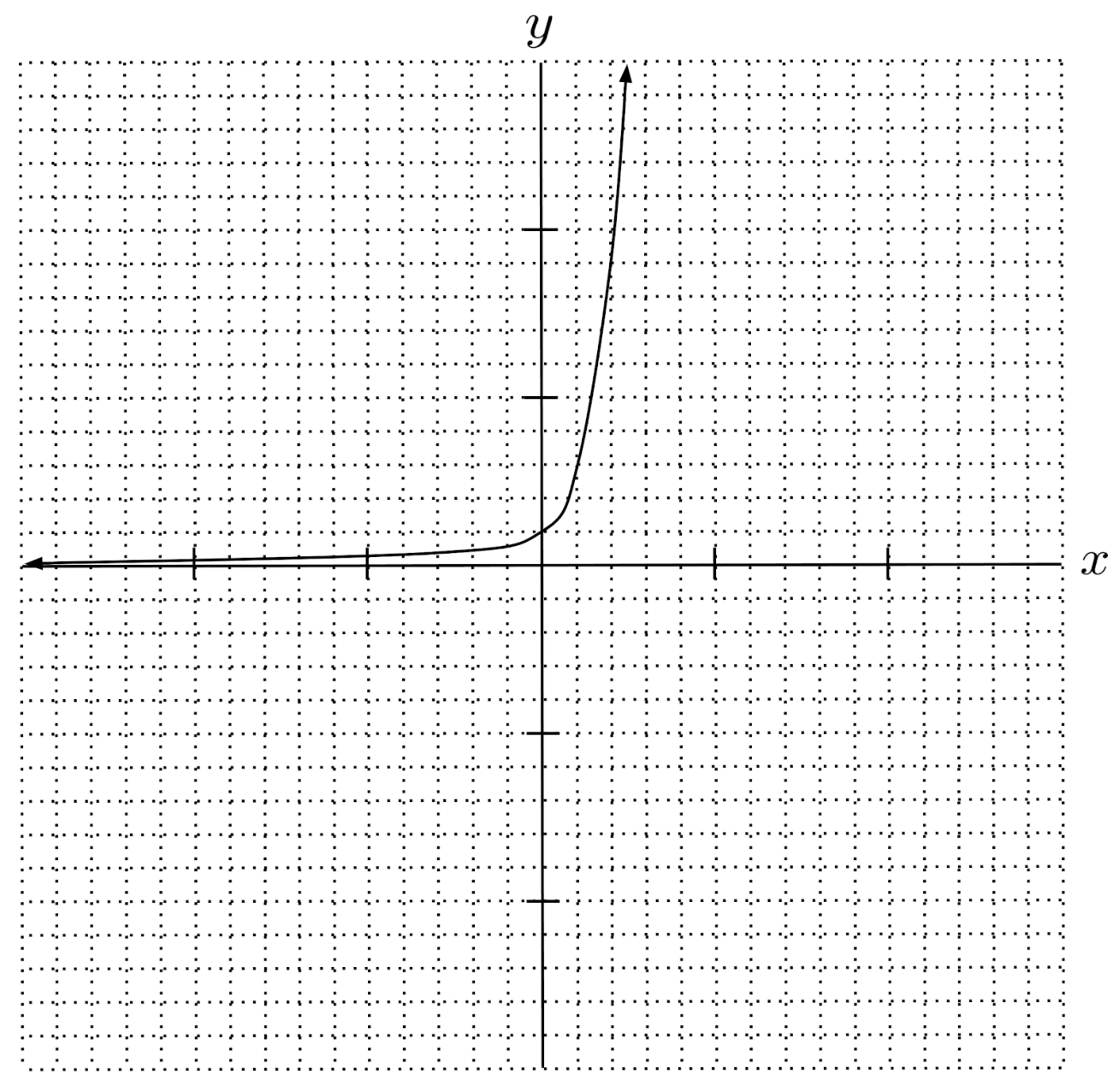
$2) \hspace{.5cm} f(x)=5^x$
Solution:
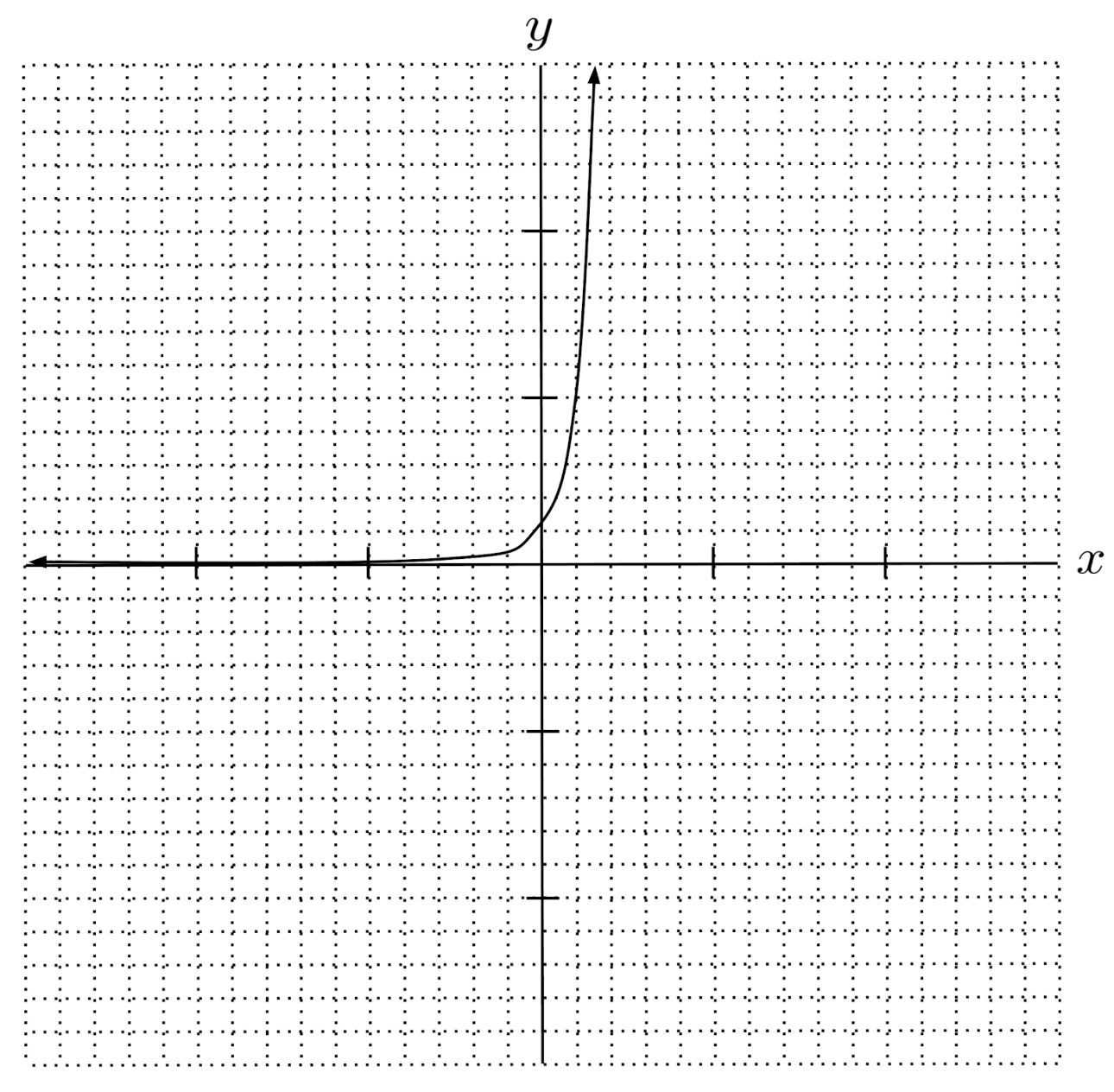
$3) \hspace{.5cm} f(x)= \left( \frac{1}{3} \right)^x$
Solution:
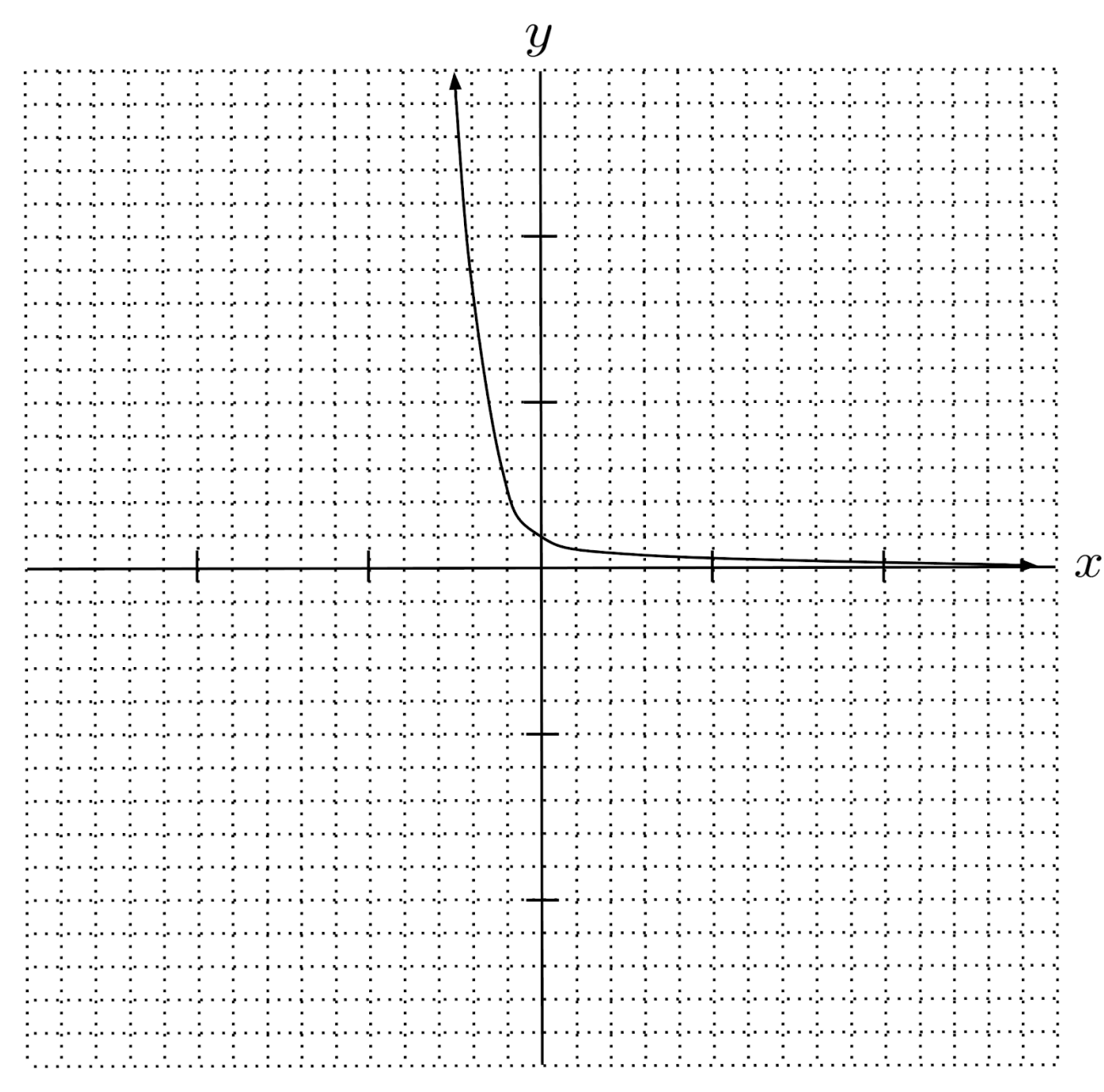
$4) \hspace{.5cm} f(x)= \left( \frac{1}{5} \right)^x$
Solution:
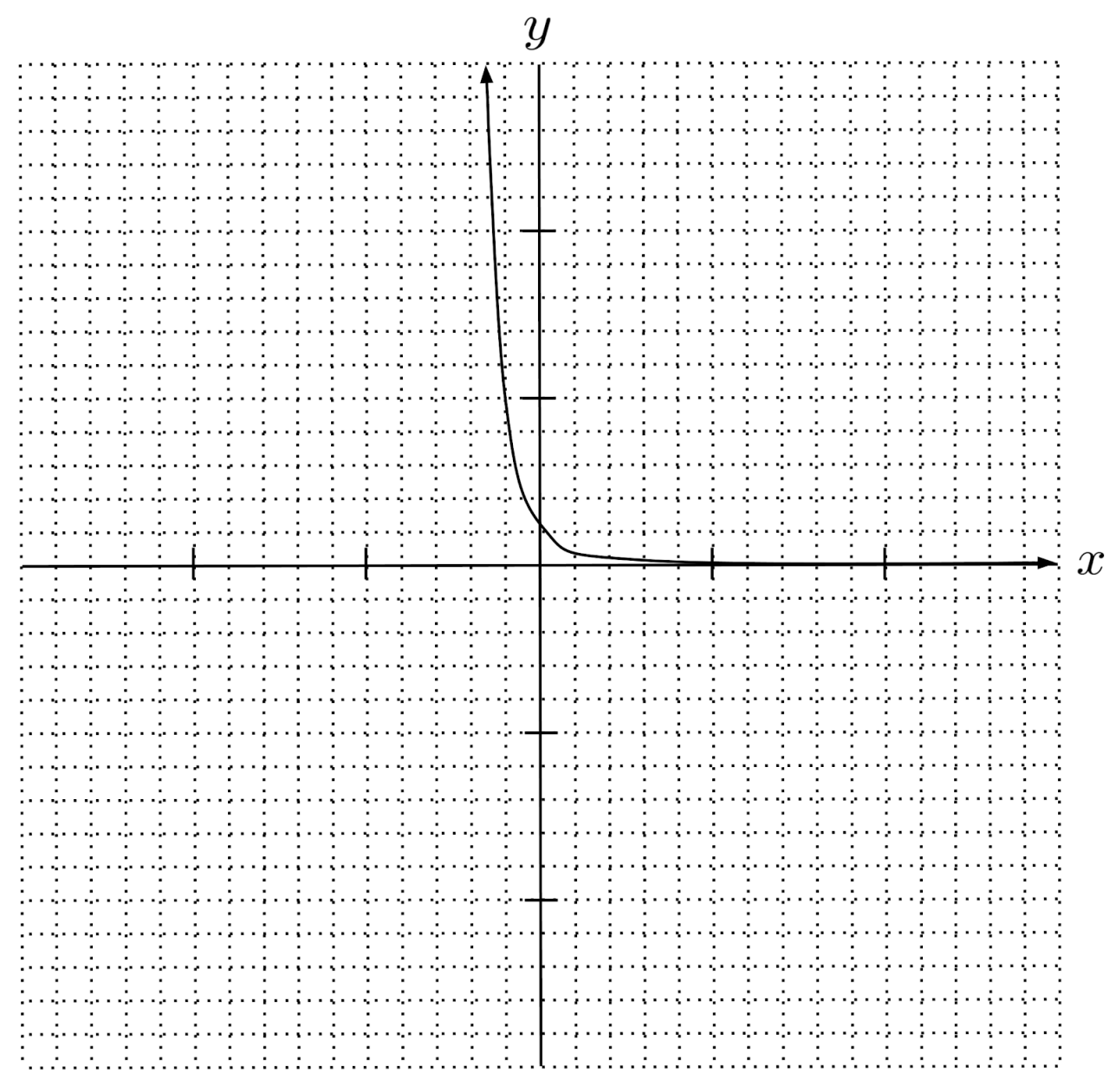
$5) \hspace{.5cm} f(x)= \left( \frac{3}{2} \right)^x$
Solution:
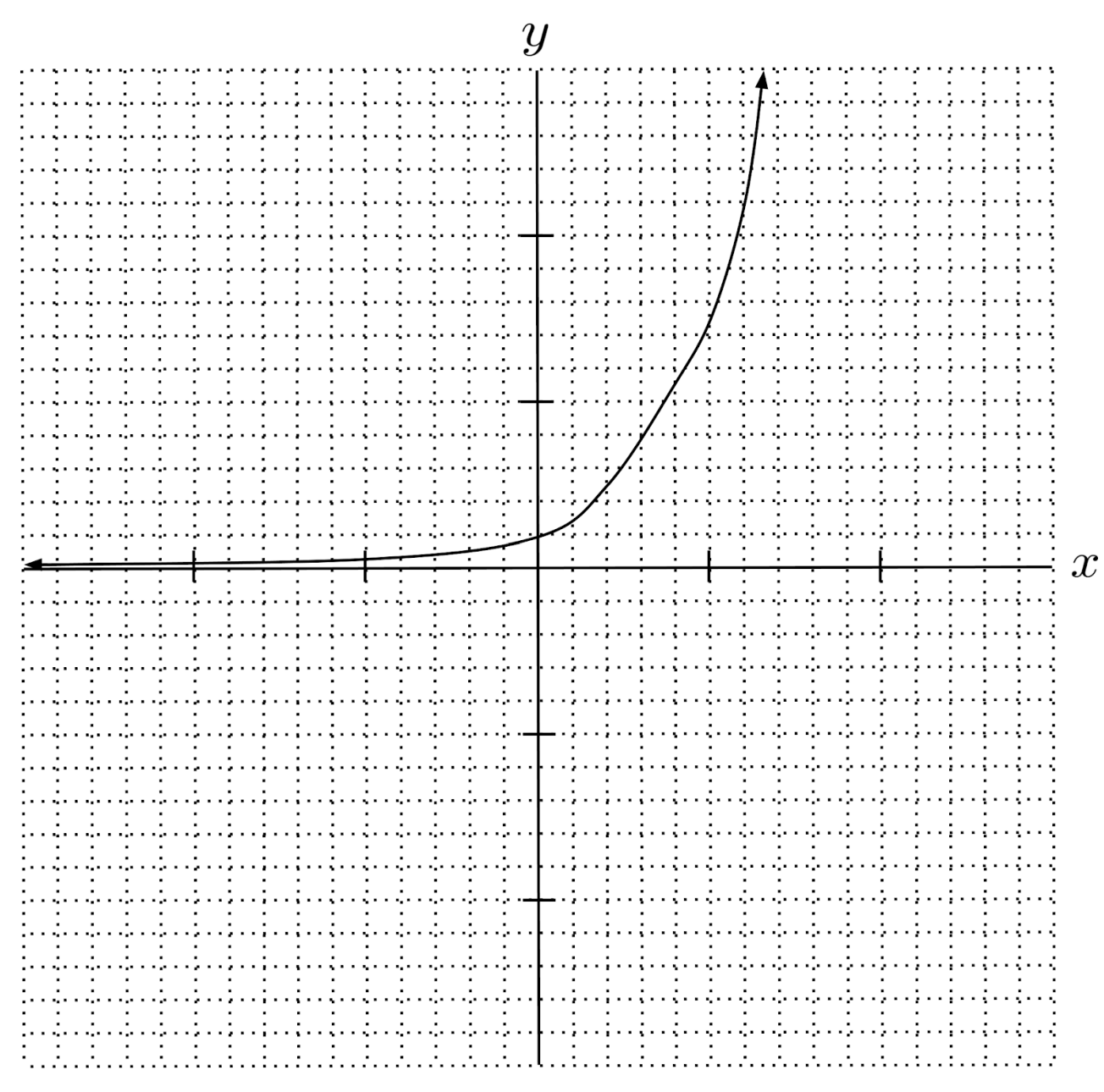
$6) \hspace{.5cm} f(x)= \left( \frac{2}{3} \right)^x$
Solution:
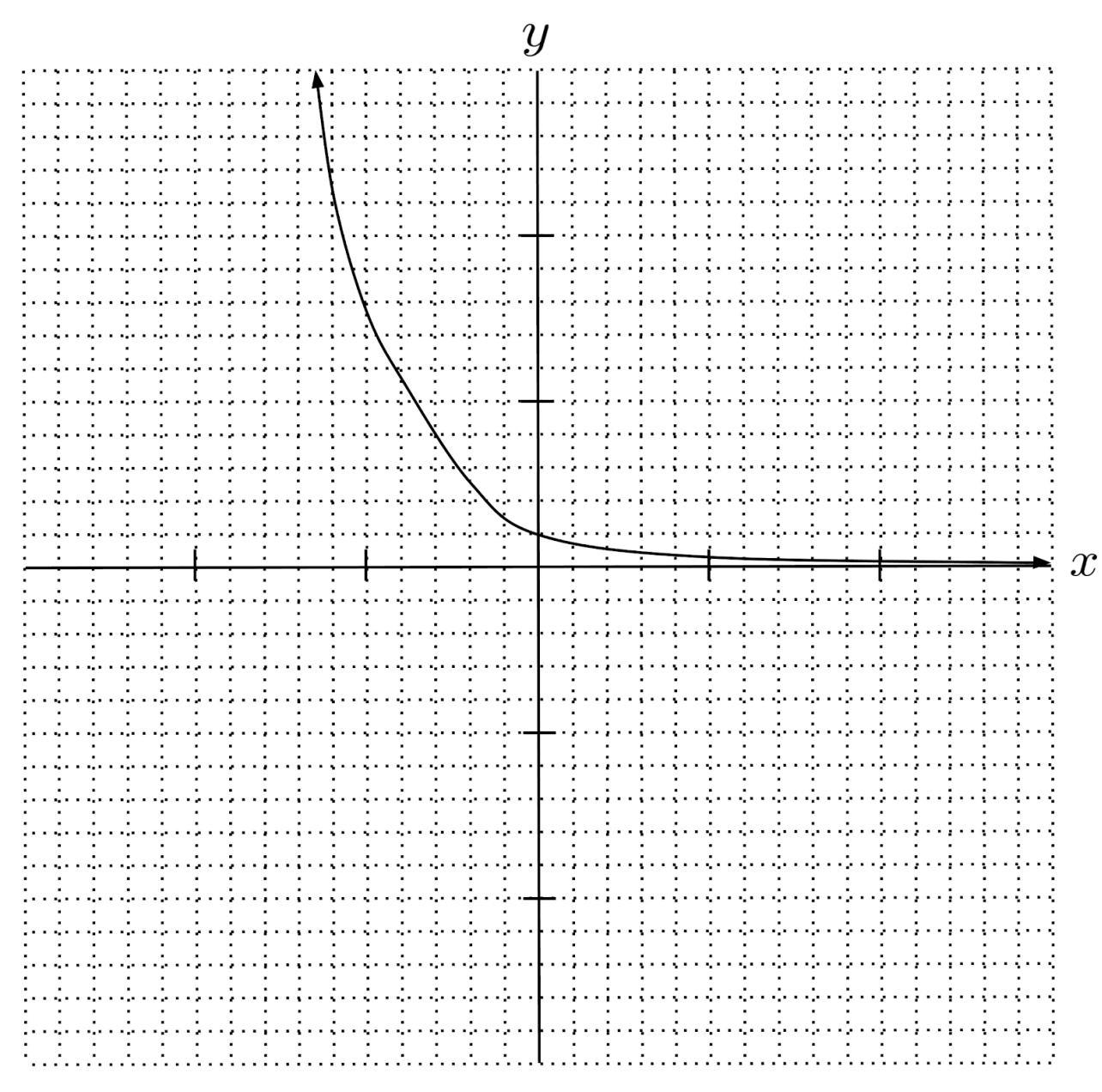
Use logarithms to solve the following exponential equations. (You can view the solution by clicking on the problem.)
$7) \hspace{.5cm} 3^x=10$
Solution:
$\log_3 10 \approx 2.096$
$8) \hspace{.5cm} 5^x=7$
Solution:
$\log_5 7 \approx 1.209$
$9) \hspace{.5cm} \left( \frac{1}{3} \right)^x=\frac{1}{10}$
Solution:
$\log_{\frac{1}{3}} \frac{1}{10} \approx 2.096$
$10) \hspace{.5cm} \left( \frac{1}{5} \right)^x = \frac{1}{2}$
Solution:
$\log_{\frac{1}{5}} \frac{1}{2} \approx 0.431$
$11) \hspace{.5cm} \left( \frac{3}{2} \right)^x = 9$
Solution:
$\log_{\frac{3}{2}} 9 \approx 5.419$
$12) \hspace{.5cm} \left( \frac{2}{3} \right)^x = \frac{1}{5}$
Solution:
$\log_{\frac{2}{3}} \frac{1}{5} \approx 3.969$
Graph the following logarithmic functions. Use logarithm rules to simplify the expression, if needed. (You can view the solution by clicking on the problem.)
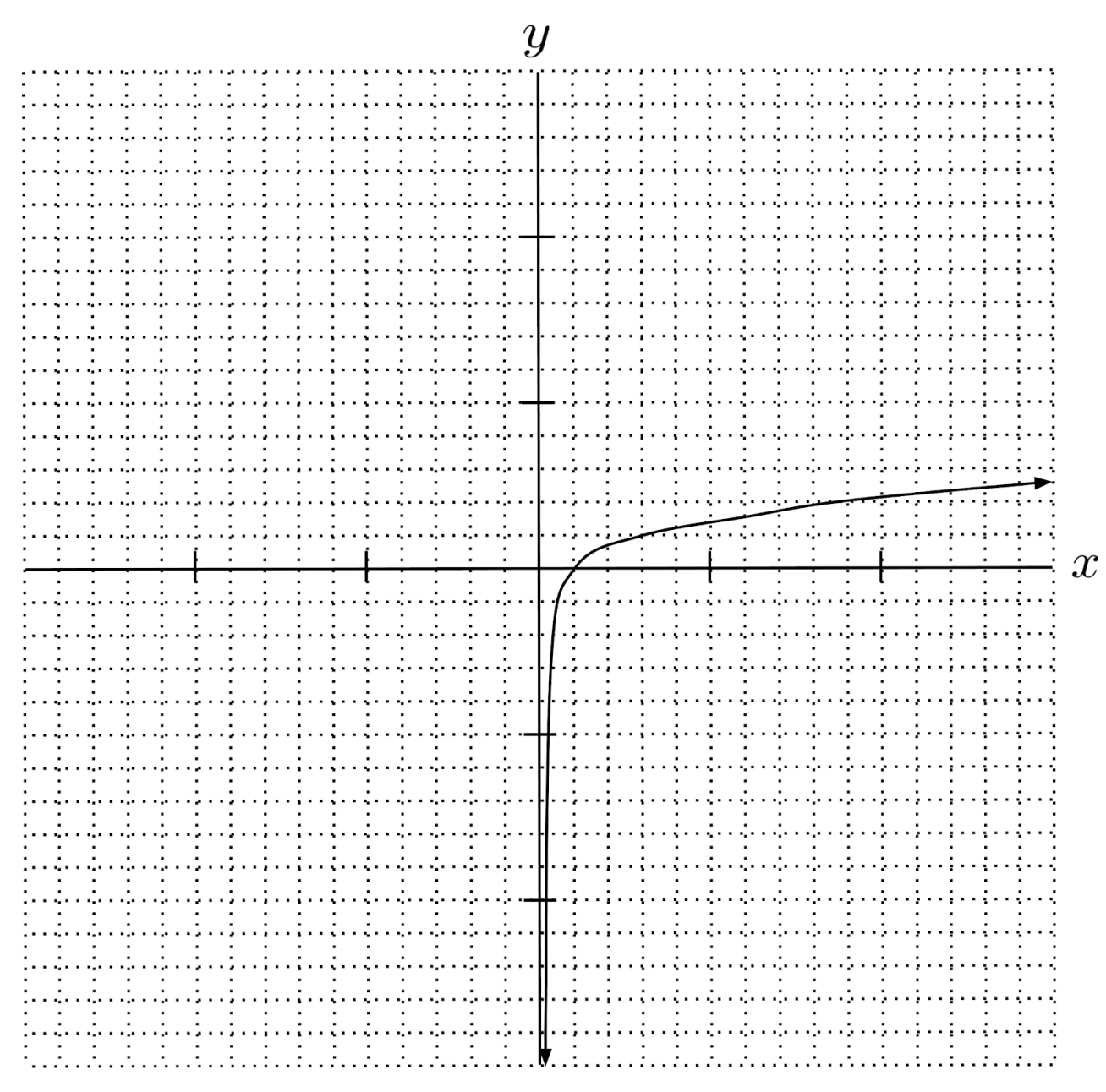
$13) \hspace{.5cm} f(x)=\log_3 x$
Solution:
$f(x) = \log_3 x$
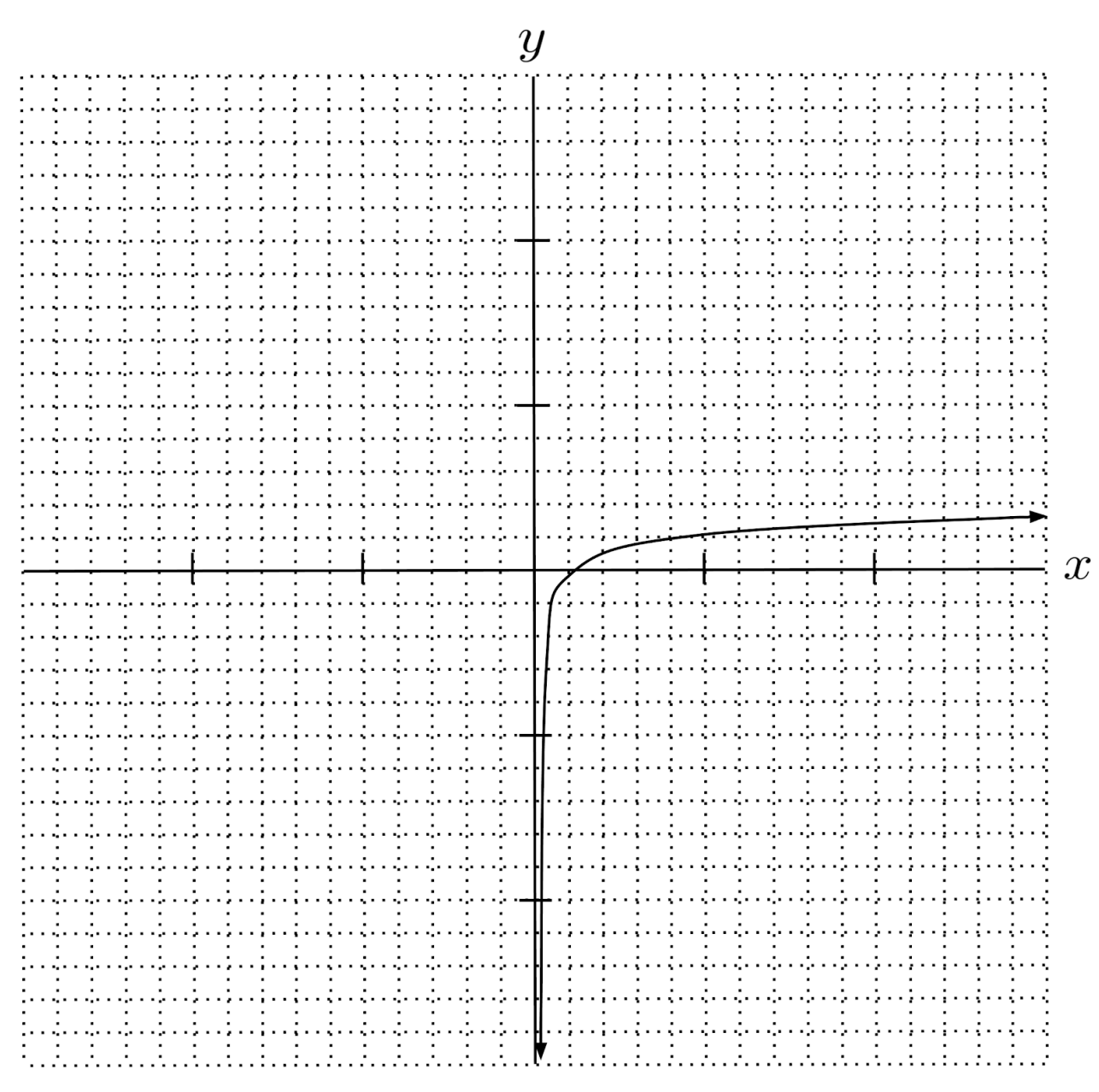
$14) \hspace{.5cm} f(x)= \log_5 x$
Solution:
$f(x) = \log_5 x$
$15) \hspace{.5cm} f(x)=\log_{\frac{1}{3}} x$
Solution:
$f(x) = \log_\frac{1}{3} x$
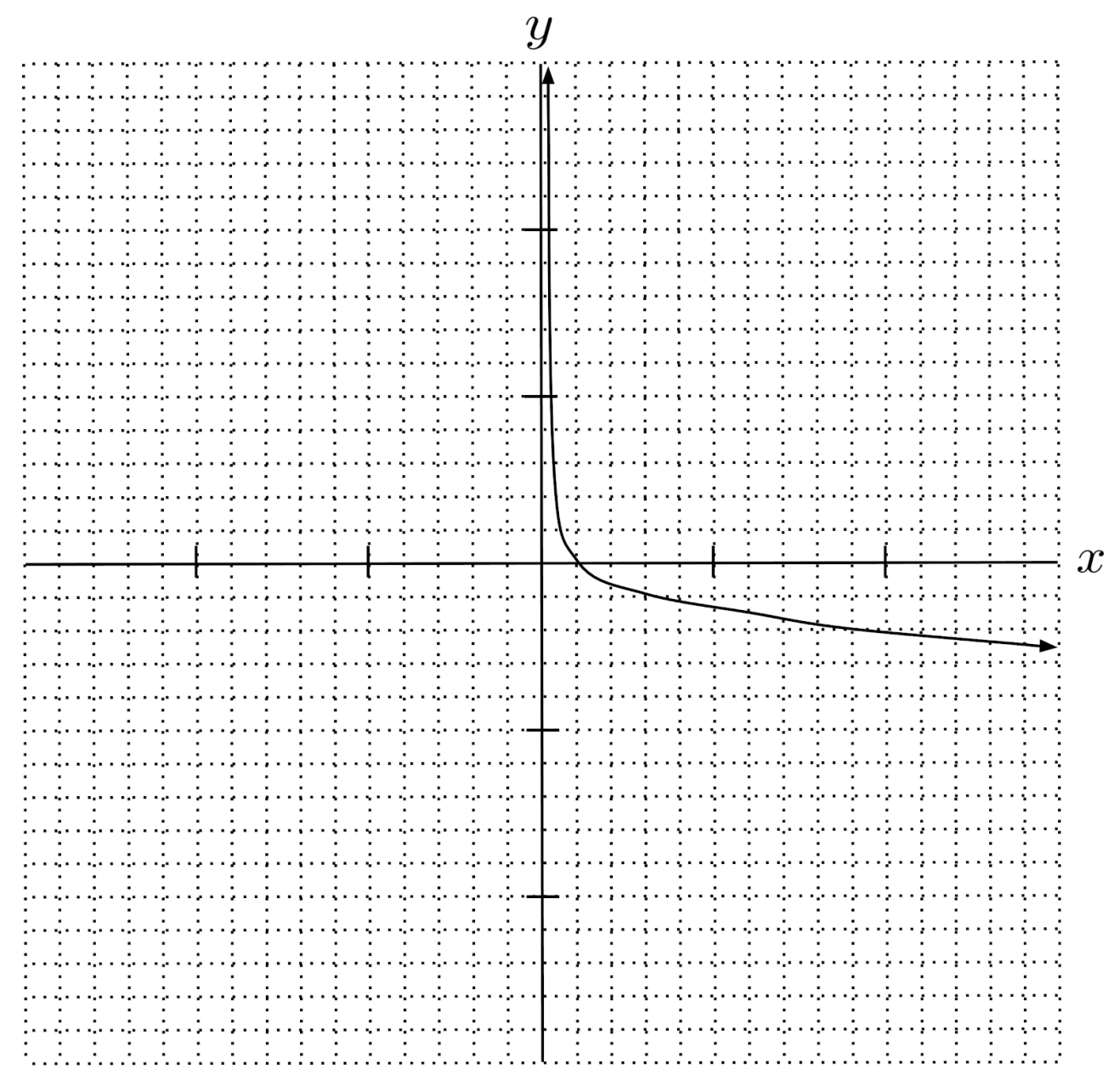
$16) \hspace{.5cm} f(x)=\log_{\frac{1}{5}} x$
Solution:
$f(x) = \log_\frac{1}{5} x$
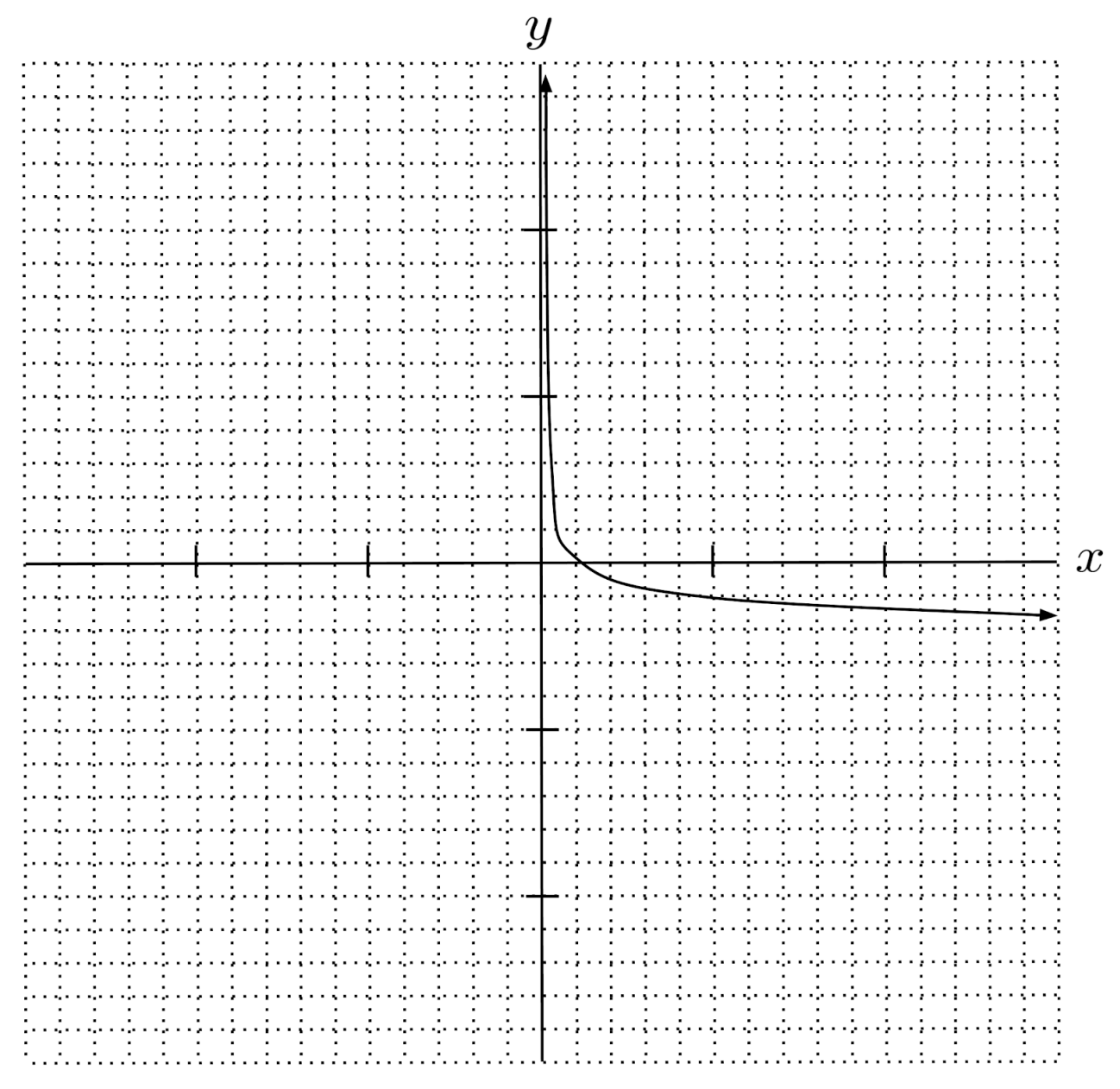
$17) \hspace{.5cm} f(x)= \log_2 \sqrt{x}$
Solution:
$f(x) = \log_4 x$
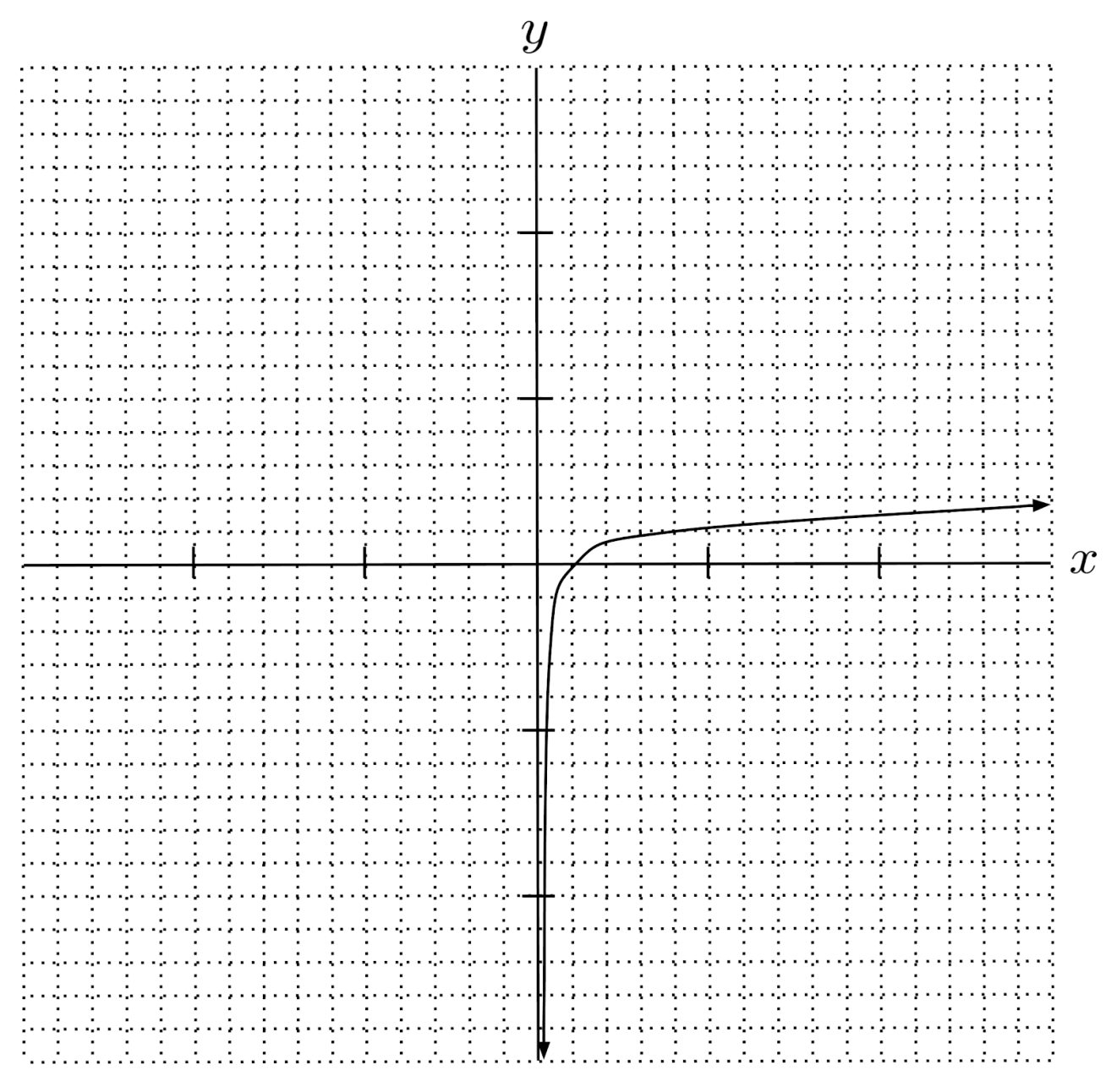
$18) \hspace{.5cm} f(x)= \log_{10} x^2 - \log_{10} x$
Solution:
$f(x) = \log_{10} x$
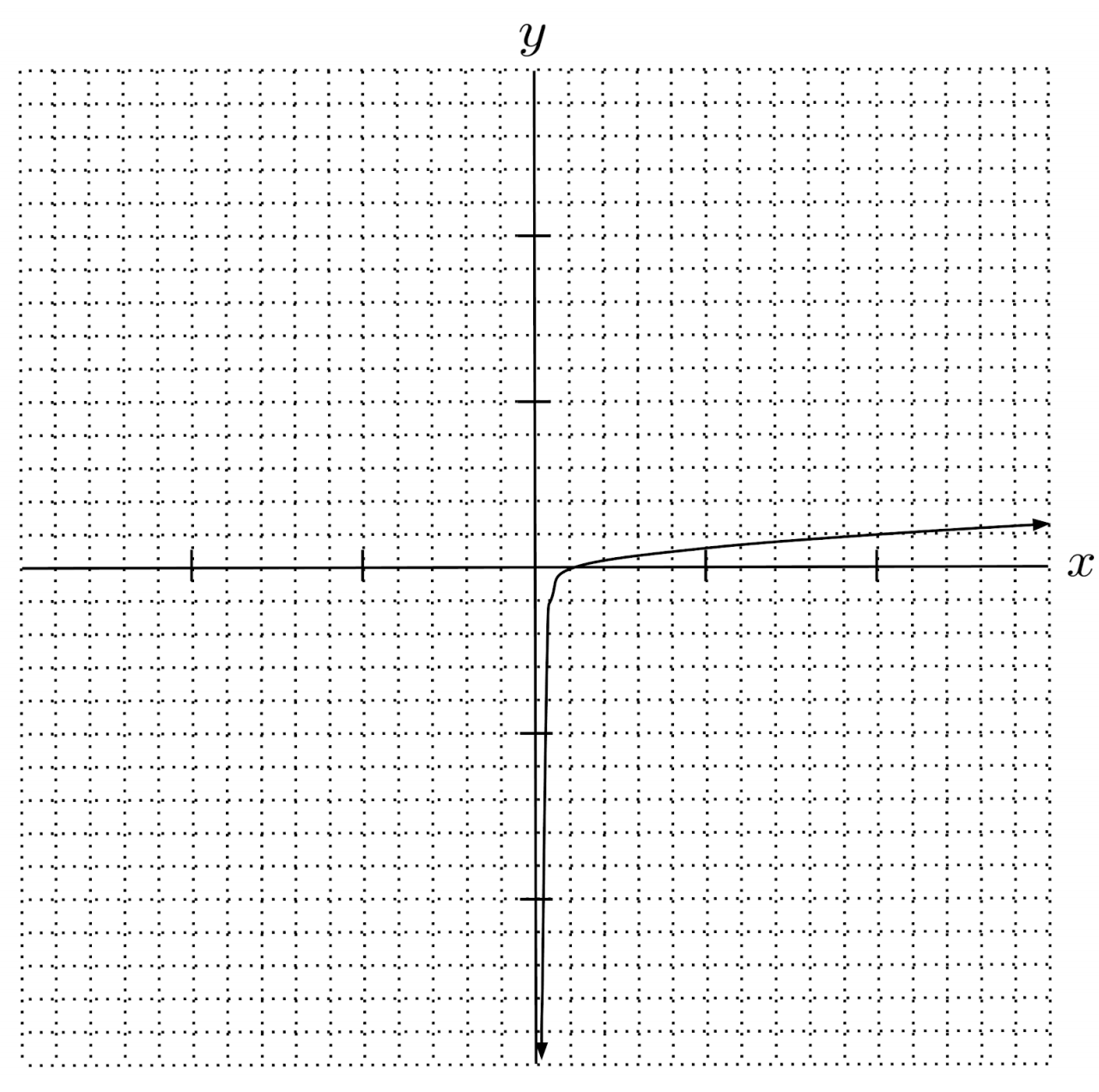
$19) \hspace{.5cm} f(x)=3 \log_3{1} + \frac{1}{2} \log_3{x}$
Solution:
$f(x) = \log_{9} x$
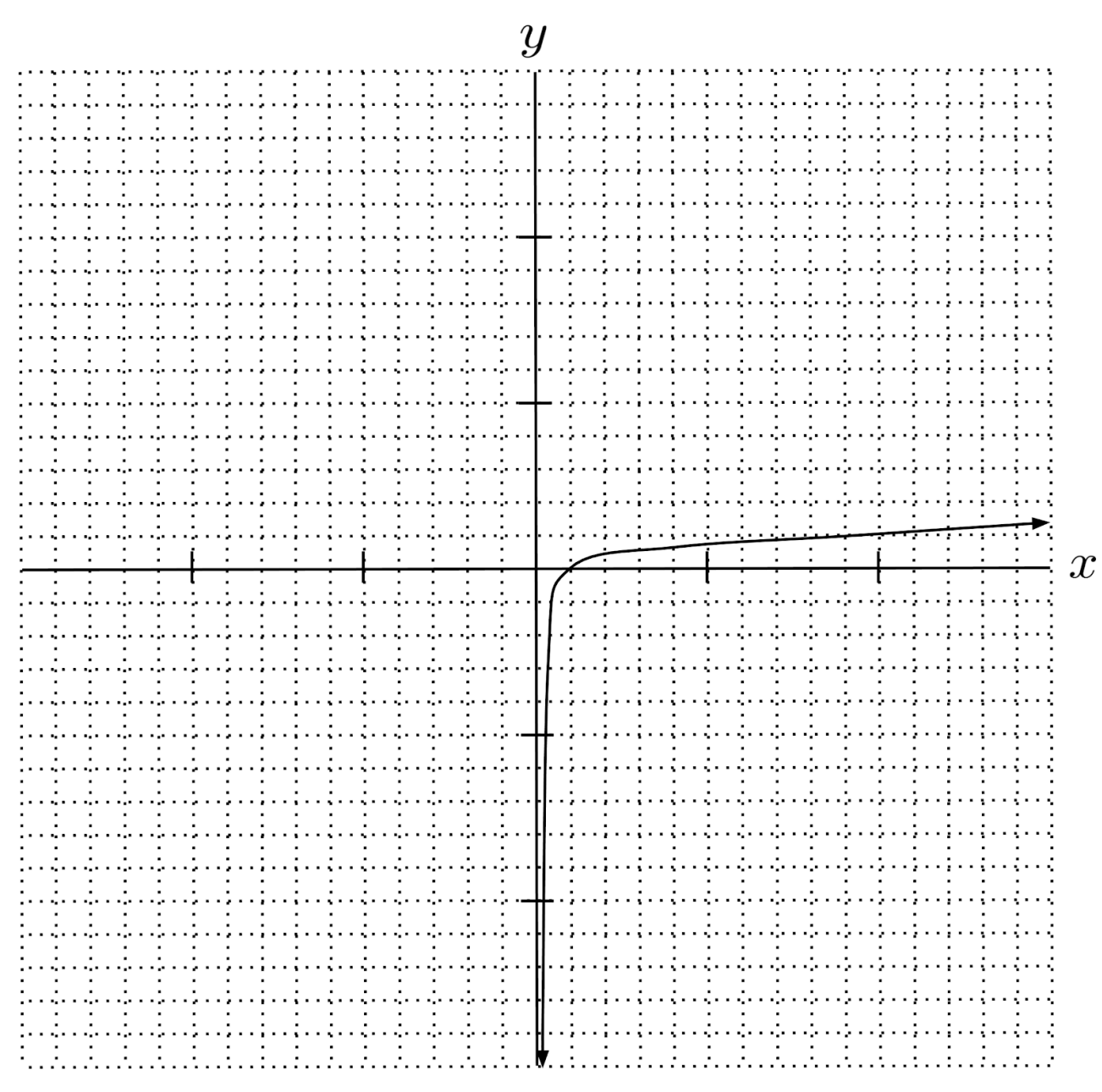
$20) \hspace{.5cm} f(x)=\log_2{x} - 2\log_4 \sqrt{x}$
Solution:
$f(x) = \log_4 x$
This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Exponential and Logarithmic Functions. In Justin Math: Algebra. https://justinmath.com/exponential-and-logarithmic-functions/