Evidence for the Existence of Dark Matter
Mass discrepancies in galaxies and clusters, cosmic background radiation, the structure of the universe, and big bang nucleosynthesis's impact on baryon density.
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.
Humans are extremely visually-oriented beings: for a great deal of us, seeing is believing. This may explain many astronomers’ skepticism when Swiss astronomer Fritz Zwicky discovered dark matter within the Coma cluster in 1933 [1,2].
However, the vast majority of scientists have come to accept the existence of dark matter as more recent studies have backed it with a plethora of evidence. Observations involving mass discrepancies in galaxies and clusters, cosmic background radiation, the structure of the universe, and the impact of big bang nucleosynthesis on baryon density all support the existence of dark matter.
Mass Discrepancies in Galaxies and Clusters
Galactic mass-to-light ratios can be calculated using the orbital velocity law ($M=\frac{rv^2}{G},$ where $M$ is the mass an object is orbiting, $r$ is the orbital radius of the orbiting object, $v$ is the object’s velocity, and $G$ is the universal gravitational constant) and the luminosity-distance formula ($L = 4 \pi r^2 b,$ where $r$ is the distance of the galaxy and $b$ is the apparent brightness of the galaxy) and have led to the conclusion that galactic matter is mostly dark and does not contribute luminosity.
To calculate a galaxy’s luminosity, the galaxy’s apparent brightness and distance from Earth are needed. A galaxy’s apparent brightness is calculated by simply measuring how bright it appears in the sky, and its distance can be determined from its velocity using Hubble’s law ($v = Hr,$ where $v$ is the galaxy’s velocity, $H$ is Hubble’s constant, and $r$ is the distance of the galaxy). The velocity can be calculated by analyzing the Doppler shifts of its light emissions: a redshifted spectrum indicates that the galaxy is moving away from us, a blueshifted spectrum indicates that the galaxy is moving toward us, and the magnitude of the spectral shift determines the magnitude of the galaxy’s velocity [1].
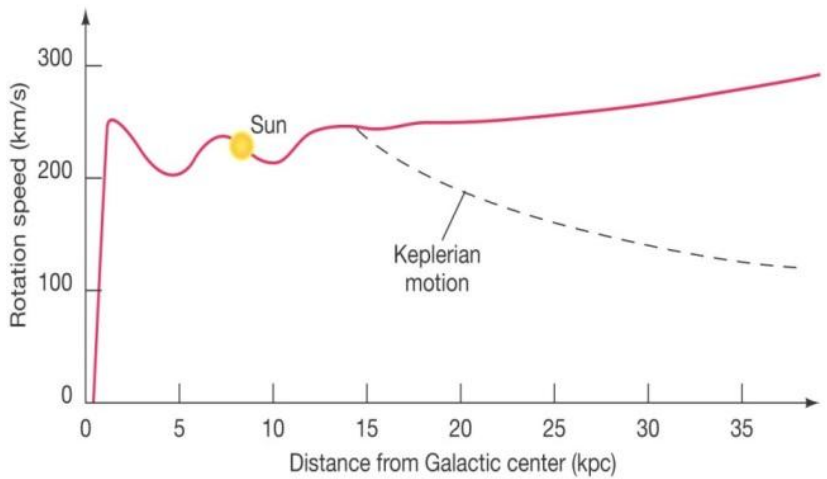
Figure 1: A rotation curve for the Milky Way galaxy. As the distance from the galactic center increases, the rotation speed slightly increases rather than decreases [3].
Because it gives the mass contained within an object’s orbit, using the orbital velocity law to calculate the mass of a galaxy requires scientists to measure the velocity and orbital radius of the farthest objects orbiting the galaxy. The outskirts of spiral galaxies are comprised of hydrogen gas, and Doppler shifts in the spectra of hydrogen gas can be analyzed to determine the gas’s velocity. Because the outskirts of spiral galaxies are very dark, the gas does not appear to orbit much more mass as its orbital radius increases. Therefore, its velocity should decrease as its orbital radius increases.
However, this is not the case: even as the radius grows, the velocity of the gas remains roughly constant (see Figure 1). This indicates that even in the dark outskirts, farther objects orbit significantly greater the amounts of mass [1]. Galactic mass-to-light ratios as high as 50 solar masses per solar luminosity imply there is a greater amount of mass in galaxies than can be accounted for by luminous matter.

Figure 2: An Einstein Ring photographed by the Hubble space telescope [5].
Another method used to determine the mass of objects in space is gravitational lensing. Gravitational lensing occurs when gravity forces light to bend around a massive object, and the amount of light distortion can be used to calculate the light-bending angle. Since the light-bending angle depends on the strength of the gravitational force bending the light, and gravitational force depends on mass, the light-bending angle can be used to calculate the mass of the lensing object.
There are several types of gravitational lensing that can be used to for this purpose, such as strong lensing, weak lensing, and flexion.
Strong lensing occurs when clusters and galaxies bend light to such an extent that it follows multiple paths around the lensing object. For example, an “Einstein Ring” forms when the background light comes from directly behind the gravitational lens (see Figure 2), and the radius of the ring is proportional to the square root of the mass of the lens. Even if the background light source is slightly off, the locations and distortions of the light can still be used to calculate the lensing object’s mass.
Weak lensing is caused by large-scale structures and although the light deflection is minimal, circular galaxies are often distorted enough that they appear as ellipses. The magnitude of distortion can be used to determine the total mass between the structure and the observer (many different clouds of dark matter contribute to the weak lensing effect, not just a single lens).
Flexion is caused by substructure and the outer areas of halos, and its amount of light distortion falls between that of strong and weak lensing. Although light is not deflected enough to make use of strong lensing mass calculation techniques and the observed area is on too small of a scale for weak lensing mass calculation techniques, there is a known relationship between mass and flexion distortion that can be used to mass the gravitational lens.
Recent studies hold the mass-luminosity ratio calculations in accord with those derived from the orbital velocity law [1], providing more significant evidence for the existence of dark matter.

Figure 3: Five Year Microwave Sky by WMAP. The color differences represent temperature fluctuations in cosmic background radiation [6].
Cosmic Background Radiation
A careful analysis of local antimatter can provide evidence for the existence of dark matter as well, since many dark matter candidates are capable of pair-annihilating. The resulting radiation [7] can be detected by cosmic ray detectors such as the Pamela telescope, which observed more positrons than initially expected in cosmic radiation, and the Fermi Large Area Telescope, which discovered an even larger excess [8]. The Fermi Gamma Ray Space Telescope detected unique gamma ray emissions coming from our galactic center, and the Wilkinson Microwave Astronomy Probe (WMAP) discovered higher levels of microwave radiation near the center of Milky Way as well [9]. These discoveries of radiation may be attributed to pair-annihilation, which could point toward dark matter.
Additionally, WMAP discovered temperature fluctuations of 0.0002 Kelvin in cosmic background radiation [10] (see Figure 3), which indicates differences in temperatures [11] and densities [12] of clumps of matter in early universe. Using such fluctuations, scientists were able to conclude that the ratio of nonbaryonic matter to baryonic matter in the universe is approximately 6 to 1 [11].
Structure of the Universe
Dark matter also plays an indispensable role in the structure of the universe. Although the universe is expanding, the space within galaxies tends to remain constant [1]. If baryonic matter had been the only type of matter, it would have been too hot to for these gravitationally bound systems to form in the time they did [13]. The gravity of dark matter would have been necessary to bring expanding matter together in this amount of time. It would have collected the first gas clouds, which would have condensed to form stars within the dark matter halos, thereby explaining the constant velocities of objects orbiting increasingly farther from the center of galaxies and clusters. The process would have then repeated with galaxies to form clusters, and it is expected to repeat with clusters to form super-clusters. This matches what we see in the universe, and scientists have evidence that super-clusters are already beginning to form [1].
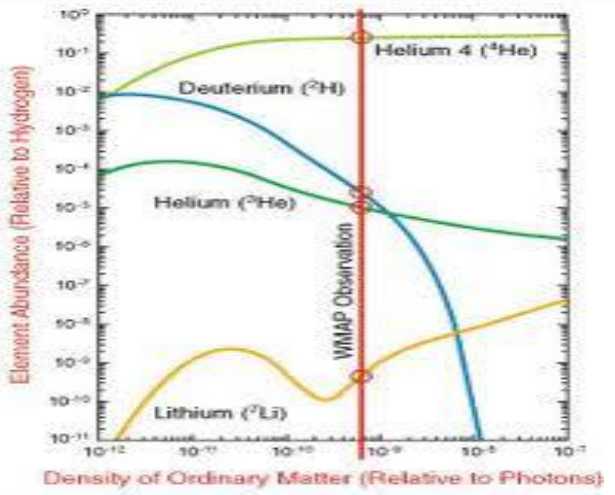
Figure 4: The abundance of elements created during the big bang is related to the density of ordinary matter in the universe [14].
Big Bang Nucleosynthesis
Lastly, dark matter is supported by the well-tested and largely accepted theory of big bang nucleosynthesis. According to the theory, the big bang produced large amounts of helium-4 and smaller amounts of deuterium, helium-3, and lithium-7. Deuterium was not produced often after the big bang because it is weakly bonded and is easily blasted apart by gamma rays, so the current amount of deuterium must be the lower limit to the amount of deuterium produced by the big bang. Knowing the cosmic background radiation temperature and that deuterium production during the big bang depended on the total amount of baryonic matter [15] (see Figure 4), big bang nucleosynthesis predicts that baryonic matter accounts for 4% of the universe’s critical density [16].
Since then, scientists have found that the total mass density of the universe is about 30% of the critical density [17]. This leaves a large amount of mass unaccounted for, which forms the basis of the Lambda-CDM model’s assertion that dark matter constitutes about 25% of the universe’s critical density [18].
Everywhere astronomers look, there is evidence for dark matter. Mass discrepancies in galaxies and clusters, cosmic background radiation, the structure of the universe, and big bang nucleosynthesis’s impact on baryon density all suggest that although we can’t directly see it, dark matter exists.
References
[1] Bennett, Jeffery, et al. The Cosmic Perspective. 3rd ed. San Francisco: Addison Wesley, 2004. 679-696. Print.
[2] Knill, Oliver. “Zwicky, Fritz.” (2006): 1. Web. 29 Sept 2012.
[3] Rotation Curve for the Milky Way Galaxy. 2010. Chart. University of Oregon Department of Physics: Astronomy 123. Web. 13 Oct 2012. (link)
[5] Einstein Ring Gravitational Lens. N.d. Photograph. HubbleSite. Web. 13 Oct 2012. (link)
[6] NASA/WMAP Science Team. Five Year Microwave Sky. N.d. Photograph. National Aeronautics and Space Administration. Web. 14 Oct 2012.
[7] Fry, Alexander. “Dark Matter Confronts Observations.” The Astronomist. N.p. 4 May 2010. Web. 29 Sept. 2012.
[8] Profumo, Stefano. “Fundamental Physics from the Sky: Cosmic Rays, Gamma Rays, and the Hunt for Dark Matter.” 18th International Symposium on Particles, Strings and Cosmology (PASCOS 2012) (2012): n.pag. ArXiv. Database. 29 Sept. 2012.
[9] Hooper, Dan, and Tim Linden. “Gamma Rays From The Galactic Center and the WMAP Haze.” Phys.Rev.D 83. (2011): n.pag. ArXiv. Database. 28 Sept. 2012.
[10] NASA/WMAP Science Team. “Fluctuations in the Cosmic Microwave Background.” National Aeronautics and Space Administration. N.p. 10 Dec. 2012. Web. 29 Sept. 2012.
[11] “Evidence for Dark Matter.” Chandra X-ray Observatory. N.p. 13 May 2012. Web. 29 Sept. 2012.
[12] NASA/WMAP Science Team. “The WMAP Achievement.” National Aeronautics and Space Administration. N.p. 16 April 2010. Web. 29 Sept. 2012.
[13] Massey, Richard, Thomas Kitching, et al. “The dark matter of gravitational lensing.” Rep. Prog. Phys. 73. (2010): n.pag. ArXiv. Database. 28 Sept. 2012.
[14] NASA/WMAP Science Team. Tests of Big Bang: The Light Elements. N.d. Chart. National Aeronautics and Space Administration.Web. 14 Oct 2012.
[15] Copi, Craig J., David N. Schramm, et al. “Big-Bang Nucleosynthesis and the Baryon Density of the Universe.” Science 267. (1995): 192-199. ArXiv. Database. 29 Sept. 2012.
[16] Grocutt, Emma. “What is Dark Matter?.” CFHTLenS. N.p., n.d. Web. 6 Oct 2012. (link)
[17] Chaisson, Eric and Steve McMillan. “Chapter Review.” Castle Rock. N.p. Web. 29 Sept. 2012. (link)
[18] Rees, Martin J. “Dark Matter: Introduction.” Phil.Trans.Roy.Soc.Lond. 361. (2003): 2427-2434. ArXiv. Database. 13 Oct 2012.
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.