Evaluating Limits

The limit of a function, as the input approaches some value, is the output we would expect if we saw only the surrounding portion of the graph.

This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Evaluating Limits. In Justin Math: Calculus. https://justinmath.com/evaluating-limits/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

The limit of a function $f(x)$, as $x$ approaches some value $a$, is the value we would expect for $f(a)$ if we saw only the portion of the graph around (but not including) $x=a$. If the resulting value is $L$, then we denote the limit as follows:

Limit vs Function Value

For example, for the function $f(x)=x^2$, the limit as $x\to 2$ is the same as the actual value of the function, which is $4$.

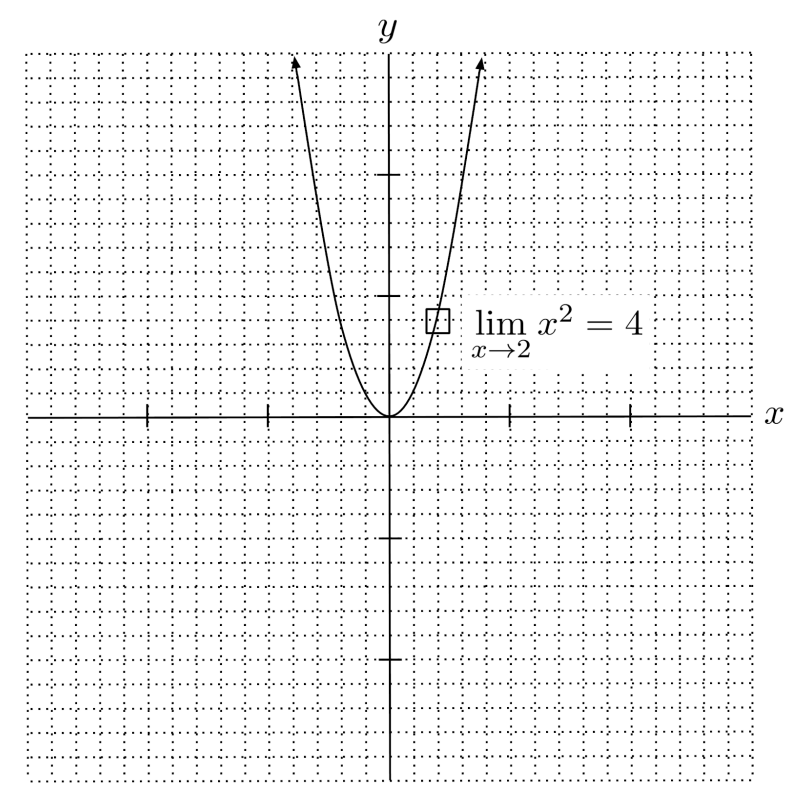
On the other hand, for the function

the limit as $x \to 2$ is not the same as the actual value of the function: the limit is $4$, while the actual value of the function is $f(x)=2$.

Remember, the limit is the value we would expect if we only saw the surrounding parts of the graph – and in this graph, the surrounding y-values get closer and closer to $4$ as the x-value gets closer and closer to $2$.

Based on this, we expect that the y-value is $4$, so we say the limit is $4$, even though our expectation here is incorrect. The limit is still $4$, and it is different from the actual function value $f(2)=1$.

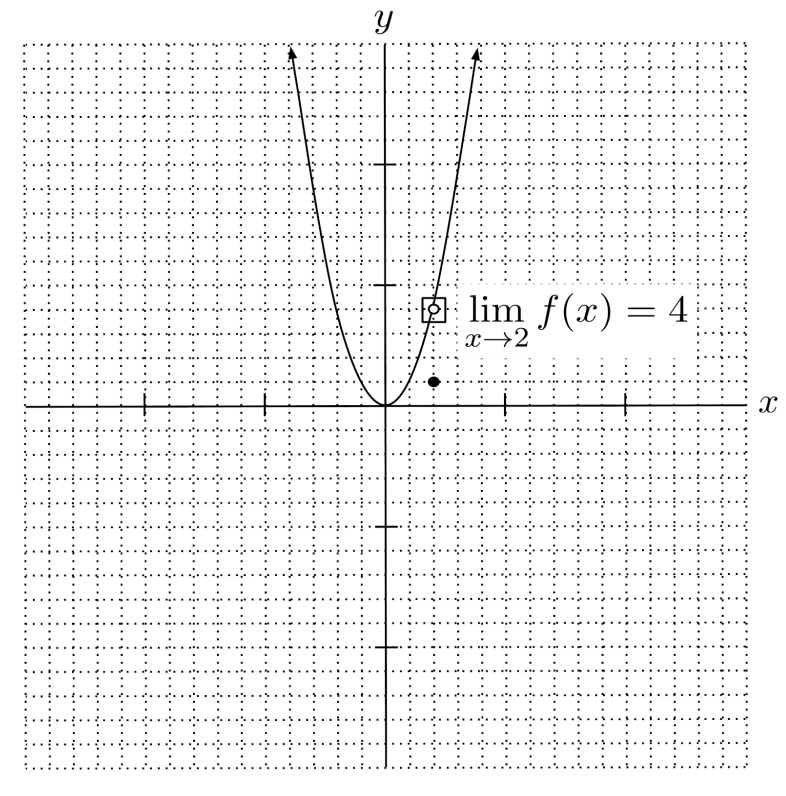
Continuity

Most of the functions we’re familiar with from algebra are continuous, meaning that the actual output value $f(a)$ is the same as the limit as $x\to a$.

However, for discontinuous functions such as some piecewise functions and rational functions, the limit as $x\to a$ might be different from the actual output value $f(a)$.

If a function can be drawn in a single stroke, then it is continuous, and the limits are the same as the function values. However, if you need to pick up your pen at some point while drawing the function, then the function is discontinuous, and some limits might be different from the actual function values.

Existence of Limits

Sometimes, limits don’t even exist. For example, for the function

the limit comes out to different values, depending on whether we approach $x\to -1$ from the left (denoted $x \to -1^-$) or the right (denoted $x \to -1^+$).

• • Coming from the left, we are on the piece $f(x)=-x-3$, so the limit is $-(-1)-3=-2$.
• • Coming from the right, we are on the piece $f(x)=x+4$, so the limit is $-1+4=3$.

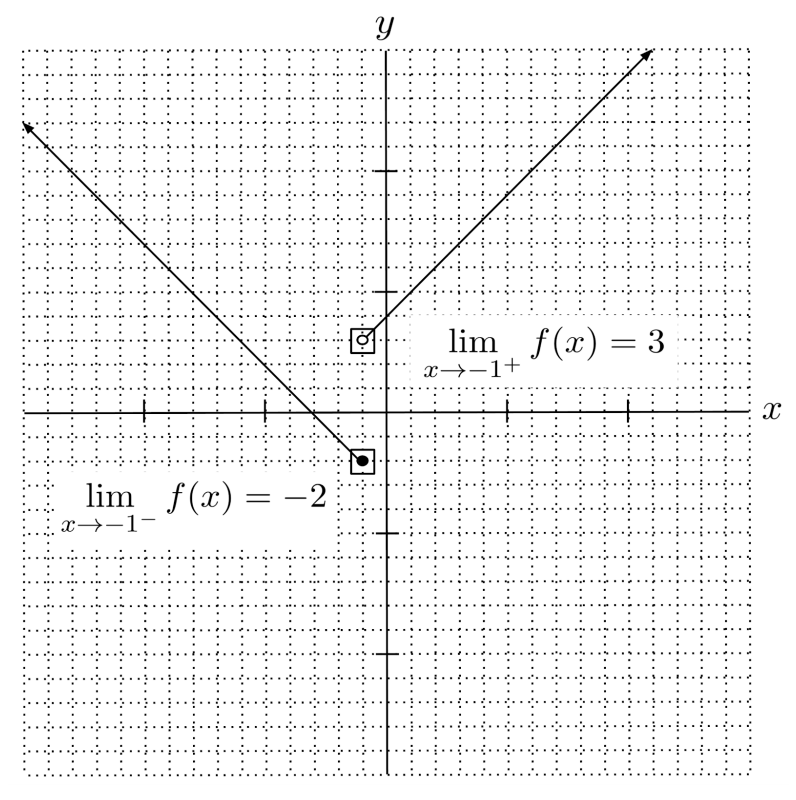
In general, a limit exists when its left and right limits are equal, and does not exist if its left and right limits are not equal.

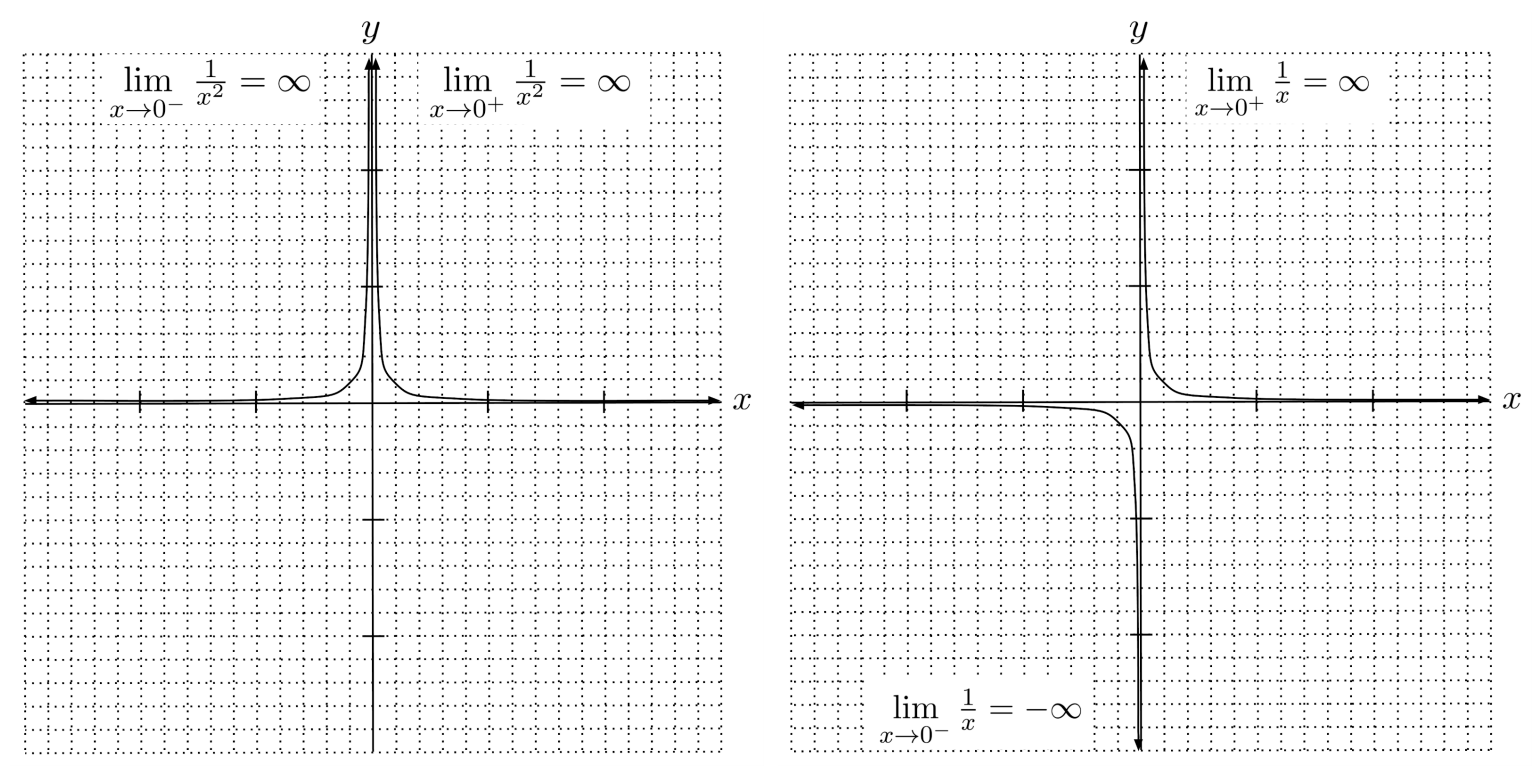
For example, for the function $f(x)=\frac{1}{x^2}$, we have $\lim\limits_{x\to 0} f(x) = \infty$ because $\lim\limits_{x \to 0^-} f(x)=\infty$ and $\lim\limits_{x \to 0^+} f(x)=\infty$.

On the other hand, for the function $f(x)=\frac{1}{x}$, we have that $\lim\limits_{x \to 0} f(x)$ does not exist because $\lim\limits_{x \to 0^-} f(x)=-\infty$ while $\lim\limits_{x \to 0^+} f(x)= \infty$.

Limits at Infinity

One exception to the rule that left and right limits must be equal is limits at infinity, i.e. limits with $x \to \infty$ or $x \to -\infty$. In this case, it doesn’t make sense to talk about a limit in more than one direction, because we can’t choose numbers greater than $\infty$, and we can’t choose numbers more negative than $-\infty$. As a consequence, limits with $x \to \infty$ are just taken as left limits ($x \to \infty^-$), and limits with $x \to -\infty$ are just taken as right limits ($x \to -\infty^+$).

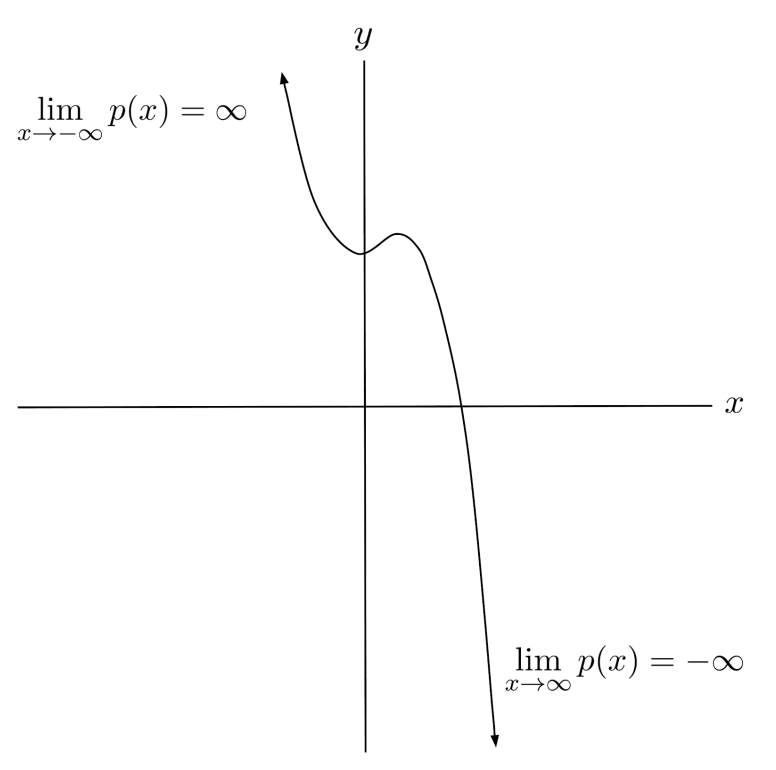
Limits at infinity can be thought of in terms of end behavior and horizontal asymptotes. For example, the polynomial $p(x)=-x^3+x^2+5$ has end behavior $p(x) \to -\infty$ as $x \to \infty$, and $p(x) \to \infty$ as $x \to -\infty$. Its limits at infinity are then $\lim\limits_{x \to \infty} p(x) = -\infty$, and $\lim\limits_{x \to -\infty} p(x) = \infty$.

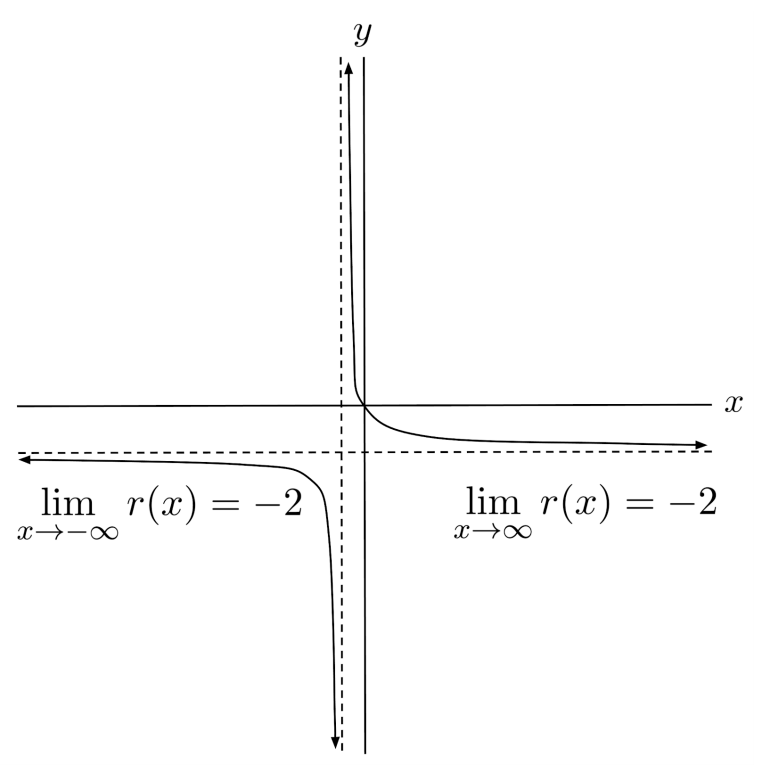
On the other hand, the end behavior of the rational function $r(x) = \frac{-2x}{x+1}$ consists of a horizontal asymptote $y=-2$. As a result, its limits at infinity are $\lim\limits_{x \to \infty} r(x)=-2$, and $\lim\limits_{x \to -\infty} r(x) = -2$.

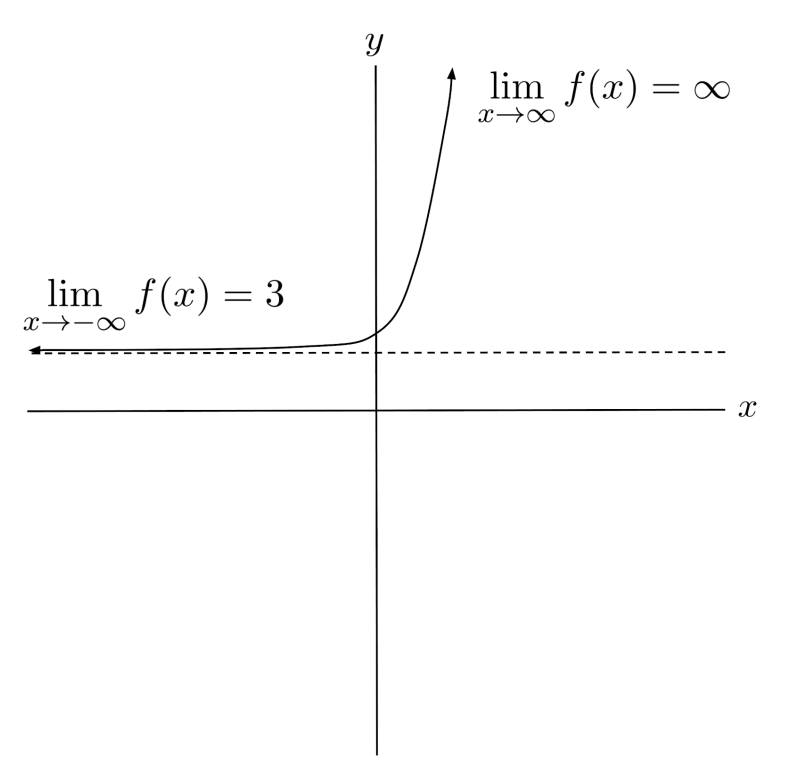
The exponential function $f(x)=2^x+3$ has mixed end behavior: it blows up to infinity as $x \to \infty$, and settles down towards an asymptote $y=3$ as $x \to -\infty$. Consequently, its limits at infinity are $\lim\limits_{x \to \infty} f(x) = \infty$, and $\lim\limits_{x \to -\infty} f(x) = 3$.

Indeterminate Form

Some limits like the one below can be difficult to think about graphically, because the function itself is difficult to graph.

At first sight, it’s not clear how the function behaves as $x$ approaches $0$. We can’t evaluate the function at $x=0$ because it is undefined there, and it’s not easy to see what happens as $x \to 0^+$ or $x \to 0^-$, since both the numerator and denominator go to $0$. (Therefore, we say that the limit is indeterminate in its current form.)

Thankfully, algebraic tricks can often be used to simplify difficult limits into easier limits. In this case, if we multiply the numerator and denominator by the conjugate of the numerator, then we can simplify the limit to a point where we are able to evaluate the function at $x=0$.

Similarly, to solve indeterminate limits where the numerator and denominator are both polynomials, we can often simplify the limit by factoring and canceling common factors:

Estimating Limits Numerically

Another trick for evaluating limits is thinking about them numerically. We can try substituting a number for $x$ that is close to the intended limit in each direction, and doesn’t make computations too hard.

For example, to evaluate the limit

numerically, we can approximate the left and right limits by substituting $x=-2.001$ and $x=-, respectively.

Both the left and right limits are approximately $-5$, so we would estimate the limit to be $-5$. Indeed, this matches the result we found earlier.

One caveat to numerical evaluation is that it always results in decimal approximations, and if the actual limit value is irrational, it can be difficult to find the exact value of the limit.

In a simple case, we might be able to recognize that an approximation of $1.4142$ actually corresponds to the value $\sqrt{2}$. However, in a trickier case, we might not be able to recognize that an approximation of $1.1547$ actually corresponds to the value $\frac{2}{\sqrt{3}}$.

Exercises

Evaluate the indicated limits. If the limit does not exist, list the left and right limits separately (if applicable). (You can view the solution by clicking on the problem.)

This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Evaluating Limits. In Justin Math: Calculus. https://justinmath.com/evaluating-limits/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.