Educational resources commonly address slant asymptotes. Why not general polynomial asymptotes?

Answer: It's not very useful (not in practice, not in theory).

Cross-posted from here.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

The Question

Back in 2018, I wrote a post about asymptotes of rational functions in which I addressed not only horizontal and slant/oblique asymptotes, but also the general case of “polynomial asymptotes.” Fast-forward over 5 years later, the post gets plenty of traffic from the query “polynomial asymptote” because apparently polynomial asymptotes are not covered anywhere else! (Below is a snippet of the post that describes what I mean by “polynomial asymptotes.”)

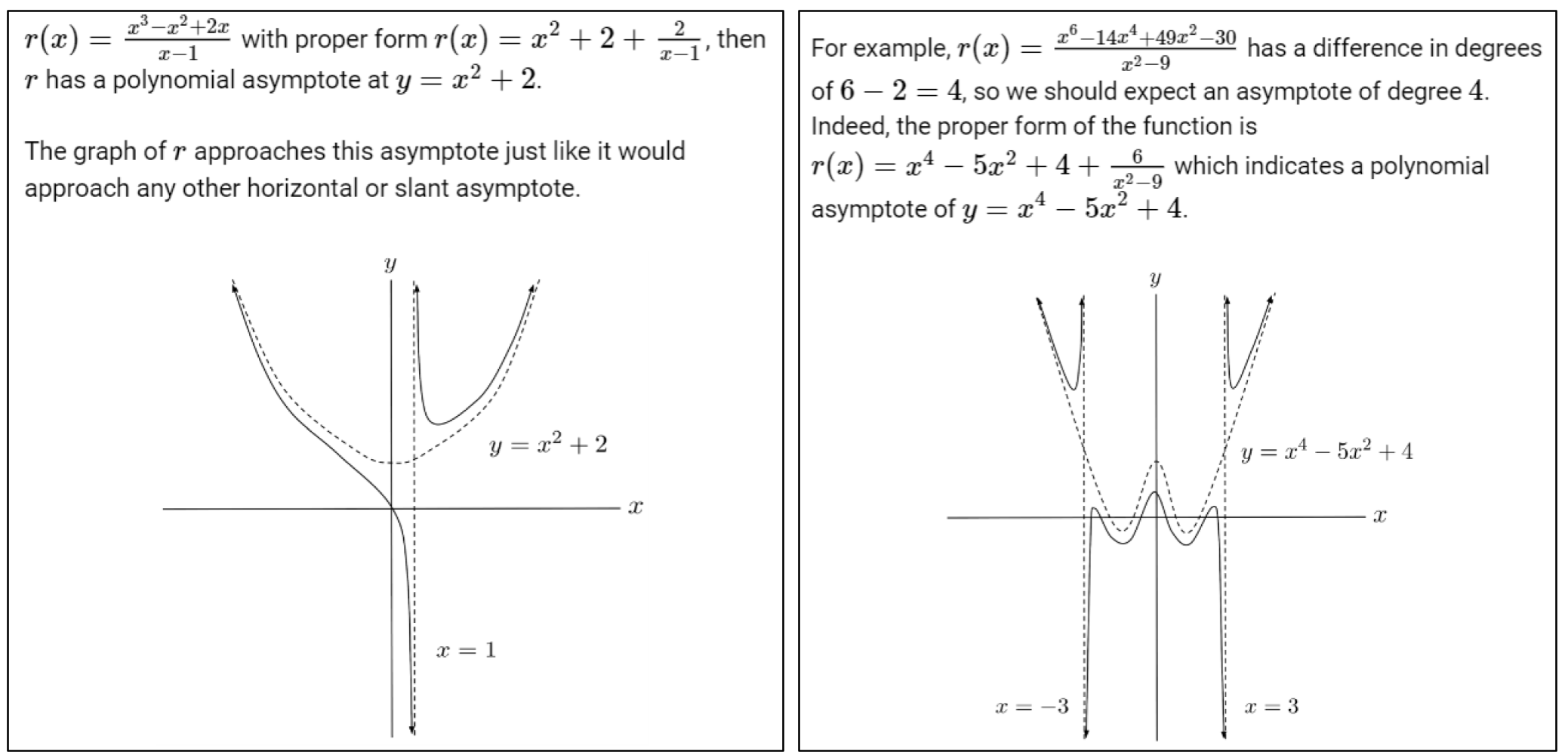
It struck me as really weird that polynomial asymptotes are not covered elsewhere. They are a natural generalization of slant asymptotes, they help develop intuition about why graphs of rational functions look like they do, and they don’t require any more advanced computation techniques –- it’s still just polynomial long division (or even synthetic division if your divisor is linear).

Why are polynomial asymptotes not normally covered by resources that teach slant asymptotes?

Falsified Hypotheses

Below are some explanations that sounded initially sounded promising, but upon deeper analysis, turned out not to be true.

• Maybe it's because people just refer to "slant asymptotes" in the most general sense, not just lines but also polynomials of degree greater than 1. False. Resources that talk about slant asymptotes generally say that "a slant asymptote occurs when the degree of the numerator is 1 more than the degree of the denominator." So I don't think that's the case.
• Maybe it's because polynomial asymptotes are just one special case in general asymptotic analysis. False. In the context of rational functions, polynomial asymptotes fully describe the general case -- they're not just a special case. And by this reasoning, it should also be uncommon to address slant/oblique asymptotes, which are actually special cases.

Accepted Hypothesis: It's Not Very Useful

It’s not very useful in practice. In practice, sketching a general polynomial is not that much easier than sketching a general rational function. And often we only care about behavior for large x, which we can easily determine by just dividing the highest-degree term of the numerator by the highest-degree term of the denominator.

It’s not very useful in theory. There’s actually not much theory that builds on polynomial asymptotes, whereas there is more theory that builds on related topics of little-o and big-O notation. So if you start with polynomial asymptotes and follow that line of thought deeper, you end up at little-o and big-O notation, for which polynomial asymptotes are not actually a prerequisite.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.