Distance and Shortest Paths in Unweighted Graphs
Using traversals to understand spatial relationships between nodes in graphs.
This post is part of the book Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. Suggested citation: Skycak, J. (2022). Distance and Shortest Paths in Unweighted Graphs. In Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. https://justinmath.com/distance-and-shortest-paths-in-unweighted-graphs/
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.
The distance between two nodes in a graph is the fewest number of edges that must be crossed to travel from one node to the other. A path between two nodes is a sequence of nodes that can be traversed to get from one node to the other, traveling along edges. The shortest path is the path with the shortest distance.
Demonstration
Below is a demonstration of distances and shortest paths in a particular graph.
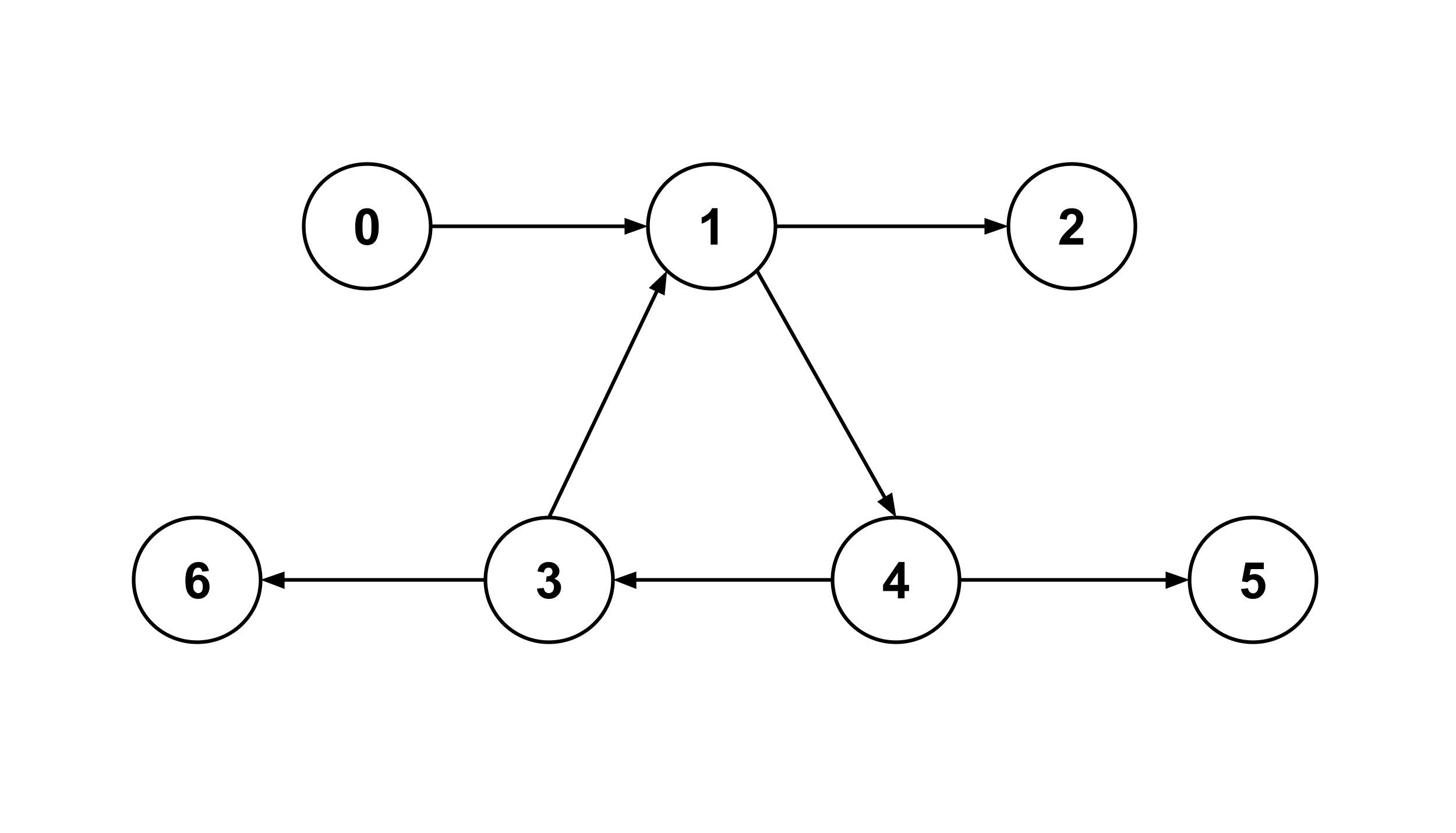
>>> graph.calc_distance(0,3)
3
>>> graph.calc_distance(3,5)
3
>>> graph.calc_distance(0,5)
3
>>> graph.calc_distance(4,1)
2
>>> graph.calc_distance(2,4)
False
>>> graph.calc_shortest_path(0,3)
[0, 1, 4, 3]
>>> graph.calc_shortest_path(3,5)
[3, 1, 4, 5]
>>> graph.calc_shortest_path(0,5)
[0, 1, 4, 5]
>>> graph.calc_shortest_path(4,1)
[4, 3, 1]
>>> graph.calc_shortest_path(2,4)
False
Implementation
The key to implementing these methods is to first create a method graph.set_distance_and_previous(idx) that does a breadth-first traversal from the node at the given index and sets the attributes node.distance and node.previous for each node encountered during the traversal.
- Start at the node whose index is
idx. - In the breadth-first traversal, you'll end up visiting all the children of that node, those children's children, and so on.
- Whenever you add a child to the queue, set the child's
previousattribute to be the parent node that the child is coming from, and set the child'sdistanceattribute to be one more than that parent's distance. - When this is all done, each node's
distanceattribute will represent its distance from the initial starting node, and each node'spreviousattribute will represent the node that comes before it if you're traveling to it on the shortest path.
Note that this will require you to write a Node class and create an instance for every node in your graph. It’s best to do this at the very beginning when you first initialize the graph.
When you run graph.calc_distance(from_idx, to_idx) or graph.calc_shortest_path(from_idx, to_idx), the first step will always be to run graph.set_distance_and_previous(from_idx). Once you have the distance and previous attributes set, you can use them to easily compute distances and shortest paths between nodes:
calc_distance(from_idx, to_idx)- simply return thedistanceattribute of the "to" node.calc_shortest_path(from_idx, to_idx)- Start at the "to" node and repeatedly go to the previous node until you get to the "from" node.
- Keep track of all the nodes you visit (this is the shortest path in reverse).
- Return the path in order from the "from" node to the "to" node. (You'll have to reverse the reversed path that you found in the previous step.)
Exercises
Extend your Graph class to include the methods calc_distance and calc_shortest_path. As always, be sure to write tests.
This post is part of the book Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. Suggested citation: Skycak, J. (2022). Distance and Shortest Paths in Unweighted Graphs. In Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. https://justinmath.com/distance-and-shortest-paths-in-unweighted-graphs/
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.