Derivatives of Non-Polynomial Functions

by Justin Skycak (@justinskycak) on January 07, 2019

There are convenient rules the derivatives of exponential, logarithmic, trigonometric, and inverse trigonometric functions.

This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Derivatives of Non-Polynomial Functions. In Justin Math: Calculus. https://justinmath.com/derivatives-of-non-polynomial-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

In this chapter, we introduce rules for the derivatives of exponential, logarithmic, trigonometric, and inverse trigonometric functions. Although it’s possible to compute each derivative using the difference quotient, it will take a long time to compute derivatives during calculus problems if we have to start from scratch with the difference quotient process every time – so it’s advantageous to remember the derivative rules. The derivative rules are to calculus, what the multiplication table is to arithmetic.

Natural Logarithm

We start with the natural logarithm, which has the derivative $(\ln x)’=\frac{1}{x}$. To see where this formula comes from, we can start by writing and simplifying the difference quotient for $\ln x$.

$\begin{align*} (\ln x)' &= \lim\limits_{\Delta x \to 0} \frac{\ln (x+\Delta x) - \ln x}{\Delta x} \\ &= \lim\limits_{\Delta x \to 0} \frac{1}{\Delta x} \left( \ln (x+\Delta x) - \ln x \right) \\ &= \lim\limits_{\Delta x \to 0} \frac{1}{\Delta x} \ln \left( \frac{x+\Delta x}{x} \right) \\ &= \lim\limits_{\Delta x \to 0} \frac{1}{\Delta x} \ln \left( 1+\frac{\Delta x}{x} \right) \\ &= \lim\limits_{\Delta x \to 0} \ln \left[ \left( 1+\frac{\Delta x}{x} \right)^\frac{1}{\Delta x} \right] \\ &= \ln \left[ \lim\limits_{\Delta x \to 0} \left( 1+\frac{\Delta x}{x} \right)^\frac{1}{\Delta x} \right] \end{align*}$

Does the limit inside the natural log look familiar? Remember that the constant $e$ can be written as the following limit:

$\begin{align*} e = \lim\limits_{u\to 0} (1+u)^\frac{1}{u} \end{align*}$

If we substitute $u=\frac{\Delta x}{x}$ and simplify/rearrange, then we can come up with an expression for the limit inside the natural log. (The limit as $\frac{\Delta x}{x} \to 0$ can be thought of as $\Delta x \to 0x$, which is the same as $\Delta x \to 0$.)

$\begin{align*} e &= \lim\limits_{\frac{\Delta x}{x} \to 0} \left( 1+\frac{\Delta x}{x} \right)^\frac{1}{\frac{\Delta x}{x} } \\ e &= \lim\limits_{\Delta x \to 0} \left( 1+\frac{\Delta x}{x} \right)^\frac{1}{\frac{\Delta x}{x} } \\ e &= \lim\limits_{\Delta x \to 0} \left( 1+\frac{\Delta x}{x} \right)^\frac{x}{\Delta x} \\ e &= \left[ \lim\limits_{\Delta x \to 0} \left( 1+\frac{\Delta x}{x} \right)^\frac{1}{\Delta x} \right]^x \\ e^\frac{1}{x} &= \lim\limits_{\Delta x \to 0} \left( 1+\frac{\Delta x}{x} \right)^\frac{1}{\Delta x} \end{align*}$

Substituting this expression into the natural log, we find that $(\ln x)’ = \frac{1}{x}$.

$\begin{align*} (\ln x)' &= \ln \left[ \lim\limits_{\Delta x \to 0} \left( 1+\frac{\Delta x}{x} \right)^\frac{1}{\Delta x} \right] \\ &= \ln \left( e^\frac{1}{x} \right) \\ &= \frac{1}{x} \end{align*}$

Knowing this, we can use the chain rule to find the derivative of any natural log function.

$\begin{align*} \left( \ln ( 2x^2+x ) \right)' = \frac{1}{2x^2+x} (2x^2+x)' = \frac{4x+1}{2x^2+x} \end{align*}$

$\begin{align*} \left( (\ln x)^2 \right)' = 2(\ln x)(\ln x)' = 2(\ln x) \left( \frac{1}{x} \right) = \frac{2\ln x}{x} \end{align*}$

General Logarithms

To differentiate a logarithmic function other than the natural logarithm, we can use the change-of-base formula to rewrite the logarithmic function in terms of natural logarithms.

For example, to find the derivative of $\log_2 x$, we can convert it into $\frac{\ln x}{\ln 2}$ and then take the derivative.

$\begin{align*} \left( \log_2 x \right)' = \left( \frac{\ln x}{\ln 2} \right)' = \frac{1}{\ln 2} \left( \ln x \right)' = \frac{1}{\ln 2} \left( \frac{1}{x} \right) = \frac{1}{x \ln 2} \end{align*}$

In general, performing this procedure on any function of the form $\log_a x$ where $a$ is a constant, we find that $(\log_a x)’ = \frac{1}{x \ln a}$.

Exponential Functions

Next, we cover exponential functions. The exponential function $e^x$ is very elegant in calculus, because its derivative is simply itself, $(e^x)’=e^x$.

To see why this is, we can start with the equation $f(x)=e^x$, then take the logarithm and derivative of both sides, and finally solve for $f’(x)$.

$\begin{align*} f(x)&=e^x \\ \ln f(x) &= x \\ \left( \ln f(x) \right)' &= (x)' \\ \frac{1}{f(x)} f'(x) &= 1 \\ f'(x) &= f(x) \\ f'(x) &= e^x \end{align*}$

Now that we know the derivative of $e^x$, we can use the chain rule to find the derivative of any exponential function.

$\begin{align*} \left( e^{x^2} \right)' = e^{x^2} (x^2)' = e^{x^2} (2x) \\ \left( \sqrt{e^x} \right)' = \left( (e^x)^\frac{1}{2} \right)' = \left( e^{\frac{1}{2}x} \right)' = \frac{1}{2}e^{\frac{1}{2}x} \end{align*}$

If we want to take the derivative of an exponential function whose base is not $e$, we can rewrite the exponential function so that its base is $e$, and then differentiate using the chain rule. For example, since $2 = e^{\ln 2}$, we see that

$\begin{align*} 2^x = \left( e^{\ln 2} \right)^x = e^{(\ln 2)x}. \end{align*}$

Now that we have a function which has base $e$, we can use the chain rule to find the derivative.

$\begin{align*} \left( 2^x \right)' = \left( e^{(\ln 2)x} \right)' = e^{(\ln 2)x} \ln 2 \end{align*}$

Using the fact that $2^x = e^{(\ln 2)x}$, we can simplify the result a bit to look like the original function.

$\begin{align*} \left( 2^x \right)' = e^{(\ln 2)x} \ln 2 = 2^x \ln 2 \end{align*}$

In general, performing this procedure on any function of the form $a^x$ where $a$ is a constant, we find that $(a^x)’ = a^x \ln a$.

Trigonometric Functions

Now, let’s talk about trig functions. Their derivatives are shown below.

$\begin{align*} \begin{matrix} (\sin x)' = \cos x & \hspace{.5cm} & (\cos x)' = -\sin x \\ (\tan x)' = \sec^2 x & & (\cot x)' = -\csc^2 x \\ (\sec x)' = \sec x \tan x & & (\csc x)' = -\csc x \cot x \end{matrix} \end{align*}$

To see why the derivative of sine is cosine, consider a section of the unit circle, where $y=\sin \theta$. If we increase $\theta$ by an infinitesimally small amount $d\theta$, the additional arc length $d\theta$ matches the hypotenuse of a triangle that has a leg $dy$ adjacent to an angle $\theta$. In this triangle, we have $\cos \theta = \frac{dy}{d\theta} = (\sin \theta)’$.

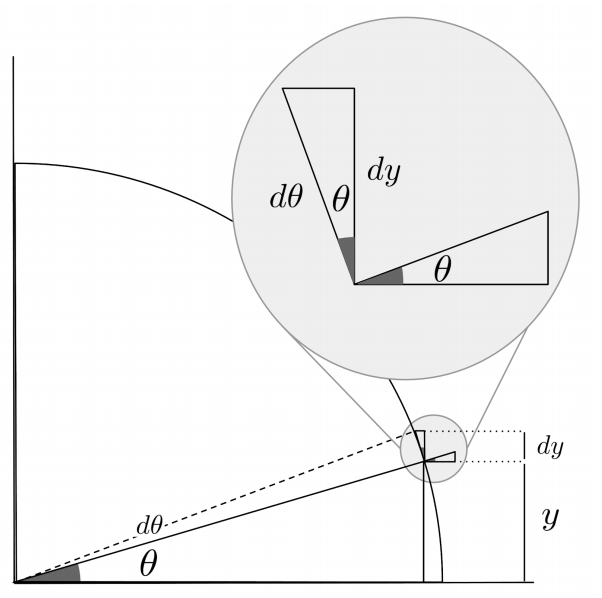
Furthermore, we can use the derivative of sine in conjunction with the identities $\cos x = \sin \left( \frac{\pi}{2} - x \right)$ and $\sin x = \cos \left( \frac{\pi}{2} - x \right)$ to compute the derivative of cosine.

$\begin{align*} \cos x &= \sin \left( \frac{\pi}{2} - x \right) \\ (\cos x)' &= \left[ \sin \left( \frac{\pi}{2} - x \right) \right]' \\ &= \cos \left( \frac{\pi}{2} - x \right) \left( \frac{\pi}{2} - x \right)' \\ &= \cos \left( \frac{\pi}{2} - x \right) (-1) \\ &= (\sin x)(-1) \\ &= -\sin x \end{align*}$

The fundamental trig derivatives are $(\sin x)’=\cos x$ and $(\cos x)’ = -\sin x$; all the other trig derivatives come from using them.

For example, to see that $(\sec x)’ = \sec x \tan x$, we express $\sec x$ as $\frac{1}{\cos x}$, take the derivative using the chain rule, and simplify.

$\begin{align*} (\sec x)' &= \left( \frac{1}{\cos x} \right)' \\ &= -\frac{1}{\cos^2 x} (\cos x)' \\ &= -\frac{1}{\cos^2 x} (\cos x)' \\ &= -\frac{1}{\cos^2 x} (-\sin x) \\ &= \frac{\sin x}{\cos^2 x} \\ &= \frac{1}{\cos x} \cdot \frac{\sin x }{\cos x} \\ &= \sec x \tan x \end{align*}$

Mnemonics

However, it will take a long time to compute derivatives if we have to start from scratch with the above process every time, so it’s advantageous to remember the table of trig derivatives.

To make it easier to remember the table, think about three key trends in the table: functions have buddies, “co” functions turn negative, and derivatives of functions other than $\sin$ and $\cos$ have two terms.

More precisely, the functions $\sin$ and $\cos$ are buddies because the derivative of $\sin$ contains $\cos$ and the derivative of $\cos$ contains $\sin$. Likewise, $\sec$ and $\tan$ are buddies because the derivative of $\sec$ contains $\tan$ and the derivative of $\tan$ contains $\sec$, and $\csc$ and $\cot$ are buddies because the derivative of $\csc$ contains $\cot$ and the derivative of $\cot$ contains $\csc$.

“Co” functions include $\cos$, $\csc$, and $\cot$, and each of their derivatives has a negative sign, whereas the other functions do not have a negative sign in their derivatives.

Lastly, if we think of squared terms as two terms being multiplied together, then $\sin$ and $\cos$ are the only functions whose derivatives consist of a single term. For example, the derivative of $\sec$ is the product of two terms $\sec$ and $\tan$, and the derivative of $\tan$ is $\sec^2$ which can be interpreted as the product of two terms $\sec$ and $\sec$. On the other hand, the derivative of $\sin$ is just a single term, $\cos$.

Just as we did for exponential and logarithmic derivatives, we can use the chain rule to take the derivative of any trig function.

$\begin{align*} \left( \sin ( \ln x ) \right)' = \cos \left( \ln x \right) \left( \ln x \right)' = \frac{\cos \left( \ln x \right)}{x} \\ \left( \sec^2 x \right)' = \left( 2\sec x \right) \left( \sec x \right)' = 2\sec^2 x \tan x \end{align*}$

Inverse Trigonometric Functions

Now that we know the derivatives of trig functions, we can use them to find the derivatives of inverse trig functions, which are shown below.

$\begin{align*} (\arcsin x)' = \frac{1}{\sqrt{1-x^2}} \\ (\arccos x)' = -\frac{1}{\sqrt{1-x^2}} \\ (\arctan x)' = \frac{1}{1+x^2} \end{align*}$

To see where these derivatives come from, we can proceed in the same way as earlier when we used the logarithmic function to find the derivative of the exponential function. We start with the equation $f(x)=\arcsin x$, then take the $\sin$ and derivative of both sides, and finally solve for $f’(x)$.

$\begin{align*} f(x) &= \arcsin x \\ \sin f(x) &= x \\ (\sin f(x))' &= (x)' \\ (\cos f(x)) f'(x) &= 1 \\ f'(x) &= \frac{1}{\cos f(x)} \\ f'(x) &= \frac{1}{\cos (\arcsin x)} \end{align*}$

To simplify the denominator, we solve for $\cos \theta$ in the identity $\sin^2 \theta + \cos^2 \theta = 1$ with $\theta = \arcsin x$.

$\begin{align*} \sin^2 \theta + \cos^2 \theta &= 1 \\ \cos^2 \theta &= 1-\sin^2 \theta \\ \cos \theta &= \pm \sqrt{1-\sin^2 \theta} \end{align*}$

We only need to consider the positive root because $\cos$ is always nonnegative on the range of $\arcsin$, which is $\left( -\frac{\pi}{2}, \frac{\pi}{2} \right]$. Substituting $\theta = \arcsin x$, our expression simplifies.

$\begin{align*} \cos \left( \arcsin x \right) &= \sqrt{1-\sin^2 \left( \arcsin x \right)} \\ \cos \left( \arcsin x \right) &= \sqrt{1-x^2} \end{align*}$

Substituting the above identity in the denominator of our derivative expression, we obtain the final result.

$\begin{align*} f'(x) &= \frac{1}{\cos (\arcsin x)} \\ f'(x) &= \frac{1}{\sqrt{1-x^2}} \end{align*}$

The rest of the inverse trig derivatives can be computed by the same process. Now, we can use the chain rule to take the derivative of any inverse trig function.

$\begin{align*} \left( \arctan ( e^x ) \right)' = \frac{1}{1+(e^x)^2} (e^x)' = \frac{e^x}{1+e^{2x} } \\ \left( (\arcsin x)^2 \right)' = 2(\arcsin x)(\arcsin x)' = \frac{2 \arcsin x}{\sqrt{1-x^2}} \end{align*}$

Exercises

Compute the derivative of each function. (You can view the solution by clicking on the problem.)

$\begin{align*}1) \hspace{.5cm} f(x)= \frac{1}{\ln x} \end{align*}$

Solution:
$\begin{align*} f'(x)= -\frac{1}{x(\ln x)^2} \end{align*}$

$\begin{align*}2) \hspace{.5cm} f(x)= e^{1+\tan x} \end{align*}$

Solution:
$\begin{align*} f'(x)= \sec^2(x)e^{1+\tan x} \end{align*}$

$\begin{align*}3) \hspace{.5cm} f(x)= 2^{\sin x}\end{align*}$

Solution:
$\begin{align*} f'(x)= (\ln 2) 2^{\sin x} \cos x \end{align*}$

$\begin{align*}4) \hspace{.5cm} f(x)= \arctan \left( \frac{1}{x} \right) \end{align*}$

Solution:
$\begin{align*} f'(x)= -\frac{1}{x^2+1} \end{align*}$

$\begin{align*}5) \hspace{.5cm} f(x)= \ln \left( \cos x^2 \right) \end{align*}$

Solution:
$\begin{align*} f'(x)= -2x \tan x^2 \end{align*}$

$\begin{align*}6) \hspace{.5cm} f(x)= \log_3 \left( \sin 2x \right) \end{align*}$

Solution:
$\begin{align*} f'(x)= \frac{2}{\ln 3} \cot 2x \end{align*}$

$\begin{align*}7) \hspace{.5cm} f(x)= \arccos \left( \log_5 x \right) \end{align*}$

Solution:
$\begin{align*} f'(x)= - \frac{1}{x \sqrt{ (\ln 5)^2 - (\ln x)^2 }} \end{align*}$

$\begin{align*}8)\hspace{.5cm} f(x) = \sin^2(x) \cos^3(x) \end{align*}$

Solution:
$\begin{align*} f'(x)= \left( \sin x \cos^2 x \right) \left( 2\cos^2 x - 3 \sin^2 x \right) \end{align*}$

$\begin{align*}9) \hspace{.5cm} f(x) = \frac{1+e^x}{1-e^x} \end{align*}$

Solution:
$\begin{align*} f'(x)= \frac{2e^x}{(1-e^x)^2} \end{align*}$

$\begin{align*}10) \hspace{.5cm} f(x) = \frac{\arcsin x}{\arccos x} \end{align*}$

Solution:
$\begin{align*} f'(x) = \frac{\arcsin x + \arccos x}{\sqrt{1-x^2} \arccos^2 x} \end{align*}$

$\begin{align*}11) \hspace{.5cm} f(x) = \arctan \left( \frac{x}{1+e^x} \right) \end{align*}$

Solution:
$\begin{align*} f'(x) = \frac{1+e^x-xe^x}{1+x^2+2e^x+e^{2x} } \end{align*}$

$\begin{align*}12) \hspace{.5cm} f(x) = \arccos(x) \arcsin^2(x) \end{align*}$

Solution:
$\begin{align*} f'(x) = \frac{ \arcsin(x) (2\arccos x- \arcsin x) }{ \sqrt{1-x^2} } \end{align*}$

$\begin{align*}13) \hspace{.5cm} f(x) = \frac{e^x}{(\ln x)^2} \end{align*}$

Solution:
$\begin{align*} f'(x) = \frac{ e^x (x \ln x - 2) }{x (\ln x)^3 } \end{align*}$

$\begin{align*}14) \hspace{.5cm} f(x) = \frac{\ln (\sin x)}{e^x} \end{align*}$

Solution:
$\begin{align*} f'(x) = \frac{ \cot x - \ln (\sin x) }{ e^x } \end{align*}$

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.