Cognitive Science of Learning: Interleaving (Mixed Practice)

by Justin Skycak (@justinskycak) on February 20, 2024

Interleaving (or mixed practice) involves spreading minimal effective doses of practice across various skills, in contrast to blocked practice, which involves extensive consecutive repetition of a single skill. Blocked practice can give a false sense of mastery and fluency because it allows students to settle into a robotic rhythm of mindlessly applying one type of solution to one type of problem. Interleaving, on the other hand, creates a "desirable difficulty" that promotes vastly superior retention and generalization, making it a more effective review strategy. But despite its proven efficacy, interleaving faces resistance in classrooms due to a preference for practice that feels easier and appears to produce immediate performance gains, even if those performance gains quickly vanish afterwards and do not carry over to test performance.

This post is part of the book The Math Academy Way (Working Draft, Jan 2024). Suggested citation: Skycak, J., advised by Roberts, J. (2024). Cognitive Science of Learning: Interleaving (Mixed Practice). In The Math Academy Way (Working Draft, Jan 2024). https://justinmath.com/cognitive-science-of-learning-interleaving/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

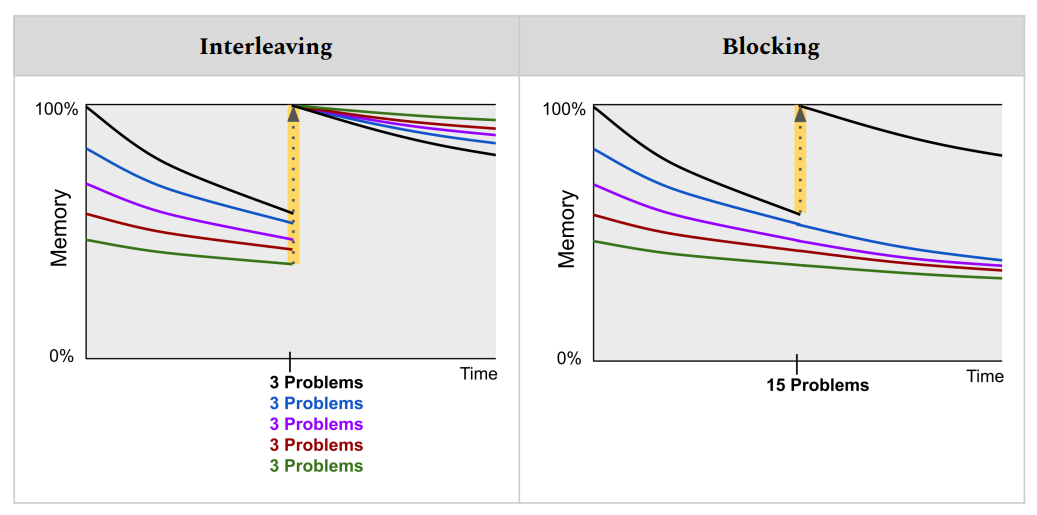
In a traditional classroom, homework assignments usually focus on a single topic. For instance, if a student learns how to subtract multi-digit whole numbers during class, then their homework might contain 15 review problems to practice that skill. This is called blocked practice or blocking, in which a single skill is practiced many times consecutively.

While some initial amount of blocking is useful when first learning a skill, blocking is very inefficient for building long-term memory afterwards during the review stage. Instead of putting those 10 review problems on a single review assignment, it would be more effective to spread them out over multiple review assignments that each cover a broad mix of previously-learned topics.

For instance, one of those assignments might have the following breakdown of problems:

(3 problems) Subtracting Multi-Digit Whole Numbers
(3 problems) Adding One-Digit Decimals
(3 problems) Converting One-Digit Decimals Into Fractions
(3 problems) Converting Improper Fractions Into Mixed Numbers
(3 problems) Solving Word Problems Using Multi-Digit Addition

This strategy is called interleaving (also known as varied practice or mixed practice).

Benefits of Interleaving

Efficiency

One benefit of interleaving is that it provides minimum effective doses of review for a handful of different topics, whereas blocked practice only hits a single topic and wastes most of the review effort in the realm of diminishing returns. As Rohrer & Pashler (2007) describe in a paper titled Increasing Retention without Increasing Study Time:

"Our results suggest that a single session devoted to the study of some material should continue long enough to ensure that mastery is achieved but that immediate further study of the same material is an inefficient use of time. ... The continuation of study immediately after the student has achieved error-free performance is known as overlearning. ... [W]hile overlearning often increases performance for a short while, the benefit diminishes sharply over time.
...
Because overlearning requires more study time than not overlearning, the critical question is how the benefits of overlearning compare to the benefits resulting from some alternative use of the same time period. ... [D]evoting this study time to the review of materials studied weeks, months, or even years earlier will typically pay far greater dividends than the continued study of material learned just a moment ago.

In essence, overlearning simply provides very little bang for the buck, as each additional unit of uninterrupted study time provides an ever smaller return on the investment of study time."

As quoted elsewhere:

"...[O]verlearning has the deficiencies of massed practice, and when the choice presents itself, our results suggest that overlearning will typically represent an inefficient use of study time." -- Pashler et al. (2007)
"...[A] typical mathematics assignment consists of many problems relating to the same skill or concept, yet evidence suggests that students receive little long-term benefit from working more than several problems of the same kind in immediate succession (e.g., Lyle, Bego, Hopkins, Hieb, & Ralston, 2020)." -- Rohrer & Hartwig (2020)

This can be visualized on forgetting curves (shown below), and it suggests an effective method to select topics for interleaved review: simply choose those topics whose spaced repetitions are due (or are closest to being due).

Discrimination and Category Induction Learning

Another benefit of interleaving is that, in addition to helping students practice carrying out solution techniques, it also enhances other types of learning that are necessary components of true mastery (see Rohrer, 2012 for a review):

(discrimination learning) matching problems with the appropriate solution techniques -- for instance, the equations $x^2 + 3x + 2 = 0$ and $x + 3x + 2 = 0$ look similar but require wildly different solution techniques.
(category induction learning) recognizing general features that distinguish problems requiring different solution techniques

As Taylor & Rohrer (2010) elaborate:

"When practice problems are blocked, however, students can successfully solve a set of practice problems without learning how to pair a problem with the skill. Indeed, because all of the problems relate to the topic -- typically the one presented in the immediately preceding lesson -- students can choose the appropriate procedure for each practice problem before they read the problem. While this reduces the difficulty of the practice problems, students are effectively relying on a crutch. Unfortunately for students, this weakness is exposed when these same kinds of problems appear on a cumulative exam, standardized test, or during a subsequent research career.

By contrast, interleaved practice gives students an opportunity to practice pairing each kind of problem with the appropriate procedure. Far from being limited to statistics courses, the difficulty of pairing a problem with the appropriate procedure or concept is ubiquitous in mathematics.

For example, the notorious difficulty of word problems is due partly to the fact that few word problems explicitly indicate which procedure or concept is appropriate. For example, the word problem, 'If a bug crawls eastward for 8 m and then crawls northward for 15 m, how far is it from its starting point'? requires students to infer the need for the Pythagorean Theorem. However, no such inference is required if the word problem appears immediately after a block of problems that explicitly indicate the need for the Pythagorean theorem (e.g. if the legs of a right triangle have lengths 8 and 15 m, what is the length of its hypotenuse?). Thus, blocked practice can largely reduce the pedagogical value of a word problem.

As a final example, it should be noted that blocked practice may facilitate students' failure to discriminate between different kinds of problems even when these kinds of problems are not superficially similar. In elementary school, for example, students are ordinarily taught to find both the greatest common factor of two integers and the least common multiple of two integers. Thus, the instructions for these two kinds of problems are easily distinguished from each other ('Find the greatest common factor ...' vs. 'Find the least common multiple ...'). However, if the practice problems of each kind are blocked, students can ignore the instruction and instead focus solely on the information that varies from problem to problem (i.e. the pair of integers). Students can then solve problems by merely repeatedly performing the same procedure without giving much thought to why it is appropriate."

Experimental Support

The benefits of interleaving are supported by numerous studies across a wide variety of domains including math, other academic subjects, raw cognitive tasks, motor skills, and even sports practice (see Rohrer, 2012 for a review). As summarized elsewhere by Rohrer (2009):

"Experiments have shown that test scores can be dramatically improved by the introduction of spaced practice or mixed practice, which are the two defining features of mixed review. Moreover, neither spacing nor mixing requires an increase in the number of practice problems, meaning that both features increase efficiency as well as effectiveness. ... Its effects on mathematics learning deserve greater consideration by teachers and researchers."

While blocking leads to more rapid gains in performance (which makes it useful when first learning a skill), interleaving promotes vastly superior retention and generalization (which makes it a more effective review strategy). As Rohrer, Dedrick, & Stershic (2015) clarify elsewhere:

"...[A] small block of problems might be optimal, especially at the outset of an assignment given immediately after students are introduced to that kind of problem, perhaps because it gives students an opportunity to focus on the execution of a strategy (e.g., procedural steps and computation). Yet students who work more than a few problems of the same kind in immediate succession are likely to receive sharply diminishing returns on their additional effort (e.g., Rohrer & Taylor, 2006; Son & Sethi, 2006)."

It’s hard to overstate how beneficial interleaving is, especially in the context of mathematics. Taylor & Rohrer (2010) found that simply interleaving practice problems, as opposed to blocking them, doubled test scores. This phenomenon was observed again by Rohrer, Dedrick, & Stershic (2015) using different, older students and more advanced math problems. As summarized by Scientific American (Pan, 2015):

"The three-month study involved teaching 7th graders slope and graph problems. Weekly lessons, given by teachers, were largely unchanged from standard practice. Weekly homework worksheets, however, featured an interleaved or blocked design. When interleaved, both old and new problems of different types were mixed together. Of the nine participating classes, five used interleaving for slope problems and blocking for graph problems; the reverse occurred in the remaining four.

Five days after the last lesson, each class held a review session for all students. A surprise final test occurred one day or one month later. The result? When the test was one day later, scores were 25 percent better for problems trained with interleaving; at one month later, the interleaving advantage grew to 76 percent."

As Rohrer, Dedrick, & Stershic (2015) elaborate further, students whose practice was interleaved also demonstrated vastly superior retention of the tested material through a delay period:

"...[A]part from its superiority to blocked practice, interleaved practice provided near immunity against forgetting, as the 30-fold increase in test delay reduced test scores by less than a tenth (from 80% to 74%).
...
Another reason for the large effects of interleaving observed here and elsewhere is that interleaved mathematics practice inherently guarantees that students space their practice. That is, in addition to the juxtaposition of different kinds of problems within an assignment, problems of the same kind are spaced across assignments."

Desirable Difficulty: Why Interleaving is Underused

It is natural to ask, then: why is interleaving so rarely leveraged in classrooms? The answer is all too familiar. In addition to deviating from traditional teaching convention, interleaving has been shown to suffer from the same misconception that plagues active learning: interleaving produces more learning by increasing cognitive activation, but students often mistakenly interpret extra cognitive effort as an indication that they are not learning as well, when in fact the opposite is true (Kornell & Bjork, 2008). Consider the following concrete example (Brown, Roediger, & McDaniel, 2014, pp.65):

"In interleaving, you don't move from a complete practice set of one topic to go to another. You switch before each practice is complete. A friend of ours describes his own experience with this:

'I go to a hockey class and we're learning skating skills, puck handling, shooting, and I notice that I get frustrated because we do a little bit of skating and just when I think I'm getting it, we go to stick handling, and I go home frustrated, saying, 'Why doesn't this guy keep letting us do these things until we get it?''

This is actually the rare coach who understands that it's more effective to distribute practice across these different skills than polish each one in turn. The athlete gets frustrated because the learning's not proceeding quickly, but the next week he will be better at all aspects, the skating, the stick handling, and so on, than if he'd dedicated each session to polishing one skill."

Blocking, on the other hand, creates a more comfortable sense of fluent learning which artificially improves practice performance by reducing cognitive activation. When practicing a single skill many times consecutively, students settle into a robotic rhythm of mindlessly applying one type of solution to one type of problem. The mindlessness is quite literal: in a study that measured “mind-wandering” during practice, people were found to mind-wander much more while blocking than while interleaving (Metcalfe & Xu, 2016). But the artificially improved practice performance tricks students into thinking that they are learning better, even though the effect quickly vanishes afterwards and does not actually carry over to test performance.

As summarized by Rohrer (2009):

"A feature that decreases practice performance while increasing test performance has been described by Bjork and his colleagues as a desirable difficulty, and spacing and mixing are two of the most robust ones. As these researchers have noted, students and teachers sometimes avoid desirable difficulties such as spacing and mixing because they falsely believe that features yielding inferior practice performance must also yield inferior learning."

In the literature, a practice condition that makes the task harder, slowing down the learning process yet improving recall and transfer, is known as a desirable difficulty. As Rohrer & Hartwig (2020) elaborate:

"Both spacing and interleaving are instances of a phenomenon known as a desirable difficulty (Bjork, 1994) -- the focus of this forum. A desirable difficulty is a learning method that, when compared to an alternative, makes practice more difficult while nevertheless improving scores on a subsequent test (e.g., Bjork & Bjork, 2014; Bjork, 2018; Bjork & Bjork, 2019; Bjork & Kroll, 2015; Schmidt & Bjork, 1992)."

Many types of cognitive learning strategies introduce desirable difficulties – for instance, Bjork & Bjork (2011) list a few more:

"Such desirable difficulties (Bjork, 1994; 2013) include varying the conditions of learning, rather than keeping them constant and predictable; interleaving instruction on separate topics, rather than grouping instruction by topic (called blocking); spacing, rather than massing, study sessions on a given topic; and using tests, rather than presentations, as study events."

However, as Rohrer & Hartwig (2020) explain, the idea of desirable difficulties can be counterintuitive:

"That difficulties can be desirable is not intuitive. In fact, many people mistakenly assume that the degree of fluency achieved during practice is a good marker of a strategy's long-term efficacy (Bjork, Dunlosky, & Kornell, 2013). Indeed, many difficulties are undesirable in that they impede not only practice performance but also test scores, as might be true for students who do homework while watching television."

Furthermore, as Robert Bjork (1994) explains, the typical teacher is incentivized to maximize the immediate performance and/or happiness of their students, which biases them against introducing desirable difficulties:

"Recent surveys of the relevant research literatures (see, e.g., Christina & Bjork, 1991; Farr, 1987; Reder & Klatzky, 1993; Schmidt & Bjork, 1992) leave no doubt that many of the most effective manipulations of training -- in terms of post-training retention and transfer -- share the property that they introduce difficulties for the learner.
...
If the research picture is so clear, why then are ... nonproductive manipulations such common features of real-world training programs? ... [T]he typical trainer is overexposed, so to speak, to the day-to-day performance and evaluative reactions of his or her trainees. A trainer, in effect, is vulnerable to a type of operant conditioning, where the reinforcing events are improvements in the [immediate] performance and/or happiness of trainees.

Such a conditioning process, over time, can act to shift the trainer toward manipulations that increase the rate of correct responding -- that make the trainee's life easier, so to speak. Doing that, of course, will move the trainer away from introducing the types of desirable difficulties summarized in the preceding section."

What’s more, most educational organizations operate in a way that exacerbates this issue:

"The tendency for instructors to be pushed toward training programs that maximize the performance or evaluative reaction of their trainees during is exacerbated by certain institutional characteristics that are common in real-world organizations.

First, those responsible for training are often themselves evaluated in terms of the performance and satisfaction of their trainees during training, or at the end of training.

Second, individuals with the day-to-day responsibility for training often do not get a chance to observe the post-training performance of the people they have trained; a trainee's later successes and failures tend to occur in settings that are far removed from the original training environment, and from the trainer himself or herself.

It is also rarely the case that systematic measurements of post-training on-the-job performance are even collected, let alone provided to a trainer as a guide to what manipulations do and do not achieve the post-training goals of training.

And, finally, where refresher or retraining programs exist, they are typically the concern of individuals other than those responsible for the original training."

Micro- and Macro-Interleaving

Macro-Interleaving

Interleaving is usually practiced within review and quiz tasks, where students interleave individual practice problems within the learning task. Lessons, on the other hand, involve minimal doses of blocked practice as this is more appropriate when a student is first learning new information.

However, by breaking up a curriculum into a massive number of bite-size, atomic lessons, it is possible to implement some degree of interleaving by doing a breadth-first (as opposed to depth-first) learning path through those lessons. I call this macro-interleaving, as opposed to micro-interleaving (which entails interleaving practice problems within a single learning task).

Most resources don’t leverage macro-interleaving. For instance, when learning calculus in a typical school, a class might spend a month on limits, then a month on derivative rules, then a month on integration techniques, then a month on sequences and series – essentially, macro-blocking. The class spends all their time on one unit at a time before declaring it “done” and moving to the next one. To leverage macro-interleaving, it would be better to split up every hour-long class into 15 minutes learning one bite-size topic in each of the 4 categories.

Micro-Interleaving

On the surface, it may appear that micro-interleaving is not fully leveraged when lessons (blocked practice) provide implicit spaced repetition credit towards component skills in need of micro-interleaved review. Shouldn’t every topic receive micro-interleaved review before appearing on a quiz?

However, this is actually the optimal solution to a crucial tradeoff.

If you want to micro-interleave the problem types within every single topic before seeing them on quizzes, then you have to do an explicit review on every single topic before seeing it on the quiz.
And if you have to do an explicit review on every single topic, then pretty soon you're going to have way too many reviews and your progress is going to grind to a halt because you're spending all your time reviewing instead of learning new material (this is a common complaint about spaced repetition systems).

So, you have to make a decision: should you

fully micro-interleave everything before quizzes, or
give up a little bit of micro-interleaving to enable spaced repetition optimizations leading to much faster progress through new material?

If you want to maximize your learning efficiency, the rate at which your learning effort gets transformed into educational progress, then option 2 is better.

Furthermore, in option 2, when engaging in repetition compression, very little micro-interleaving is actually being given up. Reviews micro-interleave not only the problem types in the original lesson, but also the component (prerequisite) skills – and reviews are specifically chosen to cover as many component skills as possible that you need practice on, so you’ll actually get an outsized dose of micro-interleaving compressed into each review.

References

Bjork, E. L., & Bjork, R. A. (2011). Making things hard on yourself, but in a good way: Creating desirable difficulties to enhance learning. Psychology and the real world: Essays illustrating fundamental contributions to society, 2(59-68).

Bjork, R. A. (1994). Memory and metamemory considerations in the training of human beings. In J. Metcalfe and A. Shimamura (Eds.), Metacognition: Knowing about knowing (pp.185-205).

Brown, P. C., Roediger III, H. L., & McDaniel, M. A. (2014). Make it stick: The science of successful learning. Harvard University Press.

Kornell, N., & Bjork, R. A. (2008). Learning concepts and categories: Is spacing the “enemy of induction”?. Psychological science, 19(6), 585-592.

Metcalfe, J., & Xu, J. (2016). People mind wander more during massed than spaced inductive learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 42(6), 978.

Pan, S. C. (2015). The interleaving effect: mixing it up boosts learning. Scientific American, 313(2).

Pashler, H., Rohrer, D., Cepeda, N. J., & Carpenter, S. K. (2007). Enhancing learning and retarding forgetting: Choices and consequences. Psychonomic bulletin & review, 14(2), 187-193.

Rohrer, D. (2009). Research commentary: The effects of spacing and mixing practice problems. Journal for Research in Mathematics Education, 40(1), 4-17.

Rohrer, D. (2012). Interleaving helps students distinguish among similar concepts. Educational Psychology Review, 24, 355-367.

Rohrer, D., Dedrick, R. F., & Stershic, S. (2015). Interleaved practice improves mathematics learning. Journal of Educational Psychology, 107(3), 900.

Rohrer, D., & Hartwig, M. K. (2020). Unanswered questions about spaced interleaved mathematics practice. Journal of Applied Research in Memory and Cognition, 9(4), 433.

Rohrer, D., & Pashler, H. (2007). Increasing retention without increasing study time. Current Directions in Psychological Science, 16(4), 183-186.

Taylor, K., & Rohrer, D. (2010). The effects of interleaved practice. Applied cognitive psychology, 24(6), 837-848.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.