CheckMySteps: A Web App to Help Students Fix their Algebraic Mistakes

by Justin Skycak (@justinskycak) on May 28, 2019

A prototype web app to automatically assist students in self-correcting small errors and minor misconceptions.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Abstract. It is inefficient for mathematics educators to manually search student work for technical mistakes. To this end, a prototype web app, CheckMySteps, has been implemented to automatically assist students in self-correcting small errors and minor misconceptions. Students enter their steps line-by-line as they solve equations or simplify expressions, and each line is checked against the previous line for mistakes. If a mistake is detected, then an example input is chosen to demonstrate the discrepancy, and feedback is generated regarding common misconceptions which may potentially form the basis of the mistake.

See below for a talk on this project:

Introduction

Many students struggle in mathematics due to technical misconceptions [1,4] in solving equations and simplifying expressions, such as forgetting to FOIL when multiplying expressions, or forgetting to divide both terms of the numerator in a fraction.

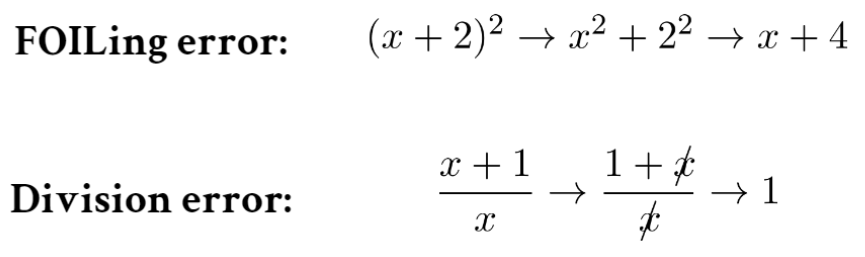
As a result, mathematics educators spend significant time and effort engaged in a repetitive process of searching student work for these misconceptions, demonstrating that they are indeed incorrect, and explaining how to correct them. This is an inefficient process, because students are sometimes able to correct their own misconceptions when given a generic explanation of their error. An extreme case of student self-correction is so-called “silly” mistakes, where the student understands a concept but makes a careless error on a question they would normally answer correctly. Students especially skilled at self-correction are sometimes even able to teach themselves new concepts, if given some guidance on what their error might be. In any case, a teacher’s time is best spent explaining misconceptions that cannot be self-corrected.

It was the goal of this project to develop a web application that automatically assists students in self-correcting small errors and minor misconceptions, thus enabling teachers to focus their time on explaining major misconceptions that cannot be self-corrected by students.

CheckMySteps

A prototype web app, CheckMySteps, was implemented as a notebook environment where students enter their steps line-by-line as they solve equations or simplify expressions (see Figure 1). Each line is checked against the previous line for mistakes, and if a mistake is detected, then an example input is chosen to demonstrate the discrepancy. Furthermore, a list of potential mistakes is displayed, which classifies the student’s mistake as a potential violation of some algebraic rule(s) and informs the student of the correct interpretation of the algebraic rule(s).

Figure 1. Screenshot of CheckMySteps interface, with sample input.

System Design

Deployment

CheckMySteps is deployed on Heroku as a Flask application. The front-end of CheckMySteps leverages an array of MathQuill [12] math fields to receive input from the user. The user is able to type math symbols using LaTeX or other intuitive key combinations (such as “<” followed by “=” to make “≤”).

The back-end of CheckMySteps leverages Sympy [14] to process mathematical expressions. An equation is processed as a pair of mathematical expressions, and is solved by setting the difference equal to zero. A set of logically joined equations (delimited by “and” or “or”) is processed using the solutions of each component equation, taking the intersection or union as appropriate. The input “no solution” is interpreted as an equation having the solution of the empty set.

Step Checking

To check whether a step in simplifying expressions is correct, the difference between the post-step and pre-step expressions is computed and simplified. The step is deemed correct if the difference simplifies to zero, and incorrect otherwise. In the event of an incorrect step, a counterexample is chosen by substituting integers [0, 1, 2, …, 9, -1, -2, …, -9, 10, 11, …, 99, -10, -11, …, -99] into the difference expression, until it evaluates to a nonzero number.

To check whether a step in solving an equation is correct, solution sets of the post-step and pre-step equations are computed. The step is deemed correct if the solution sets are identical, and incorrect otherwise. In the event of an incorrect step, a counterexample is chosen from the symmetric difference of the two solution sets.

Mistake Classification

To generate the list of potential mistakes for an incorrect step, ad-hoc mistake classification rules were used to select relevant entries from a master list of potential mistake classes and feedback descriptions.

Student mistakes in algebra often come from weakness in the fundamentals of arithmetic [4], and overgeneralizing simple rules to situations where they do not apply [1]. As such, mistake classes were chosen as arising from arithmetic weaknesses and overgeneralization of simple rules, such as distribution rules. The choices of mistake classes were also guided by several reports [5,10,11,13] detailing common algebra mistakes that educators experience in practice when working with students.

Each mistake classification rule was defined on two lines of input: the line preceding the algebraic step (called the previous line), and the line following the algebraic step (called the current line). Mistake classification rules leveraged not only the written content of these two lines, but also each line’s solution set, and the difference expression of the two lines.

For lines consisting of expressions, the difference expression was defined as the current expression minus the previous expression. For a single equation, the difference expression was defined as the left-hand side of the equation minus the right-hand side of the equation. For lines consisting of equations, the difference expression of the two equations was defined as the difference expression of the current equation, minus the difference expression of the previous equation.

More information about the potential mistakes module is provided in the appendices. Appendix 1 justifies the use of ad-hoc rules for mistake classification in CheckMySteps. Appendix 2 contains the master list of mistake classes, classification rules, and feedback descriptions used in CheckMySteps.

Validation

Mistake classification rules were validated by first manually generating example(s) for each mistake class, and then verifying that the corresponding mistake class was triggered when each example was given as input. These examples are provided along with the mistake class information in Appendix 2.

To test the general coverage of the mistake classes used, an undergraduate tutor unfamiliar with CheckMySteps was asked to generate a sample of steps containing algebraic errors based on their experiences with real-life students. These steps were supplied as input to CheckMySteps, and in 10 out of the 14 steps, CheckMySteps detected a relevant mistake class and supplied relevant feedback. The sample of erroneous steps and the relevant mistake classes detected by CheckMySteps are provided in Appendix 3.

Future Work

CheckMySteps can be improved by implementing more granular mistake classes. For example, the “Negative Sign” mistake class is triggered whenever a negative sign has been incorrectly dropped or added from one step to the next, but it does not discriminate between dropping a negative sign and adding a negative sign – both variations of the mistake are lumped into the same class. A granular set of mistake classes, where variations of similar mistakes are separated into individual classes, would provide the user with more specific information surrounding their mistake.

CheckMySteps can also be improved by implementing location-specific feedback when mistake classes are triggered, which highlights the specific term(s) in the equation or expression where the mistake occurred. A simple way to pinpoint the relevant terms in some cases may be to match terms in the difference expression with terms in the lines preceding and following the erroneous step.

Lastly, CheckMySteps can be improved by better handling equations that cannot be solved using standard algebraic techniques. Computing the solution sets of such inputs can require excessive or indefinite computation time, thus making CheckMySteps susceptible to time-out issues. Fortunately, though, such equations do not appear on algebra homeworks, where the aim is to practice solving equations that can be solved using standard algebraic techniques.

References

[1] Bagni, G. T. (2000). ‘Simple’ Rules and General Rules in Some High School Students’ Mistakes. Journal für Mathematik-Didaktik, 21(2), 124-138.

[2] Brown, J. S., & Burton, R. R. (1978). Diagnostic models for procedural bugs in basic mathematical skills. Cognitive science, 2(2), 155-192.

[3] Brown, J. S., & VanLehn, K. (1980). Repair theory: A generative theory of bugs in procedural skills. Cognitive science, 4(4), 379-426.

[4] Brown, G., & Quinn, R. J. (2006). Algebra students’ difficulty with fractions: An error analysis. Australian Mathematics Teacher, The, 62(4), 28.

[5] Dawkins, P. (2017). Common Math Errors - Algebra Errors. Paul’s Online Notes. (link)

[6] Erabadda, B., Ranathunga, S., & Dias, G. (2017, July). Automatic Identification of Errors in Multi-Step Answers to Algebra Questions. In Advanced Learning Technologies (ICALT), 2017 IEEE 17th International Conference on (pp. 215-219). IEEE.

[7] Gonzalez, C. S., Guerra, D., Sanabria, H., Moreno, L., Noda, M. A., & Bruno, A. (2010). Automatic system for the detection and analysis of errors to support the personalized feedback. Expert Systems with Applications, 37(1), 140-148.

[8] Hoppe, H. U. (1994). Deductive error diagnosis and inductive error generalization for intelligent tutoring systems. Journal of Interactive Learning Research, 5(1), 27.

[9] Huang, Z., & Tokuda, N. (1996). A syntactical approach to diagnosing multiple bugs in an intelligent tutoring system. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 26(2), 280-285.

[10] Schechter, E. (2009). The Most Common Errors In Undergraduate Mathematics. (link)

[11] Scofield, T. (2003). Top Algebra Errors Made By Calculus Students. (link)

[12] Seoul-Oh, H., & Adkisson, J. (2016). MathQuill. (link)

[13] Steig, J. (1999). Common Mistakes in Algebra. (link)

[14] Meurer, A., et al. (2019). Sympy: symbolic computing in Python. PeerJ Computer Science, 103(3)

Appendix 1: Justification of Ad-Hoc Rules

In the past, math learning systems have approached the problem of error diagnosis through the use of procedural networks [2], whose nodes represent granular steps in a problem-solving procedure, and whose edges reflect how the steps may be arranged in sequence. By including edges that correspond to underlying procedural bugs, the problem of diagnosing an error reduces to the problem of identifying the path through the network. Furthermore, knowledge of common misconceptions is not a vital prerequisite to using procedural networks: potential procedural bugs can be generated systematically by deleting node(s) from the network and introducing buggy edges to traverse any breaks in connectivity [3].

Procedural networks work well for modeling errors in arithmetic, because arithmetic is represented by a procedural network that is finite and acyclic. In such a network, there are finitely many buggy procedural paths and they can all be enumerated easily. Student errors can then be classified according to the bug that best predicts the student’s answers.

On the other hand, procedural networks offer less of an advantage for modeling errors in algebra, because algebra is represented by a procedural network that is infinite and permits cycles. There are often multiple procedures by which one can solve an algebra problem, and there are always infinitely many valid manipulations that one may perform on an algebraic equation or expression (though many of them may be unhelpful in traveling towards a solution). As a result, the procedural network for algebra contains infinitely many buggy procedural paths, and thus fails to simplify the problem of error diagnosis.

An alternative to procedural networks is ad-hoc error diagnosis [6,7,8,9], where a set of common errors are chosen using domain knowledge, and an error detector is hand-crafted for each individual error. Ad-hoc rules are often tailored to particular forms of algebraic input, such as linear or quadratic equations, and can achieve error classification accuracy comparable to that of human teachers within their domain of intended input [6]. However, as a result of being tailored to particular forms of input, ad-hoc rules tend not to generalize well to arbitrary algebraic input, such as equations containing rational and non-polynomial terms.

Appendix 2: Mistake Classes, Examples, Detection Rules, and Feedback Descriptions

Each mistake class is listed below, together with feedback for the mistake, an example of the mistake, and a rule for detecting the mistake. Any particular mistake detection and feedback can be observed, for example, by entering the provided mistake example as input into CheckMySteps.

Distribution of Exponentiation: Exponentiation distributes over all terms of a product or quotient, but cannot be distributed over a sum or difference.

Mistake Example: $(x+2)^2 \rightarrow x^2+4$
Detection Rule: Previous line has parentheses followed by exponent.

Distribution of Multiplication: Multiplication distributes over all terms of a sum or difference, but only to a single term of a product, and only to the first term of a quotient.

Mistake Example: $2(x+1) \rightarrow 2x+1$
Detection Rule: Previous line has parentheses and Distribution of Exponentiation has not been triggered.

Exponent of 0: Raising anything to the power of 0 gives a result of 1.

Mistake Example: $x^0 \rightarrow 0$
Detection Rule: Difference expression evaluates to 1 or -1 and previous line has a zero exponent.

Self-Division: Dividing anything by itself gives a result of 1.

Mistake Example: $\frac{x}{x} \rightarrow 0$
Detection Rule: Difference expression evaluates to 1 or -1 and previous line contains division and Exponent of 0 has not been triggered.

Square Root of Square: Taking the square root of a squared expression results in the absolute value of that expression.

Mistake Example: $\sqrt{x^2} \rightarrow x$
Detection Rule: Difference expression evaluates to $x-\sqrt{x^2}.$

Negative Exponent: A negative exponent $x^{-n}$ is equivalent to the fraction $\frac{1}{x^n}.$

Mistake Example: $x^{-2} \rightarrow -x^2$
Detection Rule: Previous line contains negative exponent.

Consecutive Exponentiation: When an exponentiated expression is exponentiated once more, the exponents are multiplied.

Mistake Example: $\left( x^2 \right)^3 \rightarrow x^5$
Detection Rule: Previous line contains consecutive exponentiation.

Multiplication with Common Bases: When an exponentiated term is multiplied by another exponentiated term that shares the same base, the exponents are added.

Mistake Example: $\left( x^2 \right) \left( x^3 \right) \rightarrow x^6$
Detection Rule: Previous line contains at least 2 exponents and Consecutive Exponentiation has not been triggered.

Negative Sign: Check for any dropped or unnecessary negative signs.

Mistake Example: $x+1=0 \rightarrow x=1$
Detection Rule: A nonzero current solution is the negative of a previous solution.

Arithmetic: Check for any mistakes in simple arithmetic.

Mistake Example: $x+5=13 \rightarrow x=9$
Detection Rule: Difference expression is constant.

Positive or Negative Root: If $x^2 = a,$ then $x = \pm \sqrt{a}.$

Mistake Example: $x^2=1 \rightarrow x=1$
Detection Rule: Previous line is an equation that contains an exponent, and a nonzero current solution is the negative of a previous solution.

Division by Variable: Dividing by a variable $x$ can cause you to lose a solution $x=0.$ Try factoring out the variable instead.

Mistake Example: $x^2=x \rightarrow x=1$
Detection Rule: Previous line has a solution 0 but current line does not have a solution 0.

Multiplication by Variable: Multiplying by a variable $x$ can cause you to introduce an invalid solution $x=0.$ Try factoring out a $\frac{1}{x}$ instead.

Mistake Example: $\frac{1}{x}=0 \rightarrow x=0$
Detection Rule: Current line has a solution 0 but previous line does not have a solution 0.

Partial Cancellation within Fraction: A factor cannot be cancelled out from the numerator and denominator of a fraction unless every term contains that factor.

Mistake Example: $\frac{x+2}{x} \rightarrow 2$
Detection Rule: Difference expression contains a fraction.

Distribution/Factoring of Root: Roots distribute over products and quotients, but not sums nor differences. Terms cannot be factored out of a root, but roots can be distributed over multiplication.

Mistake Example: $\sqrt{x+2} \rightarrow \sqrt{x}+\sqrt{2}$$, $$\sqrt{2x} \rightarrow 2\sqrt{x}$
Detection Rule: Difference expression contains at least one root.

Distribution/Factoring of Absolute Value: Absolute value distributes over products and quotients, but not sums nor differences. Negative terms cannot be factored out of an absolute value, but absolute value can be distributed over multiplication.

Mistake Example: $\vert x+2 \vert \rightarrow \vert x \vert + \vert 2 \vert,$ $\vert -2x \vert \rightarrow -2 \vert x \vert$
Detection Rule: Difference expression contains at least one absolute value.

Distribution/Factoring of Sine: Sine does not distribute over sums, nor differences, nor products, nor quotients, nor exponents. Terms cannot be factored out of sine.

Mistake Example: $\sin(x+2) \rightarrow \sin(x) + \sin(2),$ $\sin(2x) \rightarrow \sin(2)\sin(x),$ $\sin(x^2) \rightarrow \sin(x)^2,$ $\sin(2x) \rightarrow 2\sin(x)$
Detection Rule: Difference expression contains at least one sine.

Distribution/Factoring of Cosine: Cosine does not distribute over sums, nor differences, nor products, nor quotients, nor exponents. Terms cannot be factored out of cosine.

Mistake Example: $\cos(x+2) \rightarrow \cos(x) + \cos(2),$ $\cos(2x) \rightarrow \cos(2)\cos(x),$ $\cos(x^2) \rightarrow \cos(x)^2,$ $\cos(2x) \rightarrow 2\cos(x)$
Detection Rule: Difference expression contains at least one cosine.

Distribution/Factoring of Tangent: Tangent does not distribute over sums, nor differences, nor products, nor quotients, nor exponents. Terms cannot be factored out of cosine.

Mistake Example: $\tan(x+2) \rightarrow \tan(x) + \tan(2),$ $\tan(2x) \rightarrow \tan(2)\tan(x),$ $\tan(x^2) \rightarrow \tan(x)^2,$ $\tan(2x) \rightarrow 2\tan(x)$
Detection Rule: Difference expression contains at least one tangent.

Distribution/Factoring of Logarithm: Logarithms do not distribute over sums, nor differences, nor products, nor quotients, nor exponents. Terms cannot be factored out of logarithms. However, multiplication inside logarithms can be converted to addition outside logarithms through the rule $\log(ab) = \log(a) + \log(b).$

Mistake Example: $\log(x+2) \rightarrow \log(x) + \log(2),$ $\log(2x) \rightarrow \log(2)\log(x),$ $\log(x^2) \rightarrow \log(x)^2,$ $\log(2x) \rightarrow 2\log(x)$
Detection Rule: Difference expression contains at least one logarithm.

Distribution/Factoring of Natural Log: Natural log does not distribute over sums, nor differences, nor products, nor quotients, nor exponents. Terms cannot be factored out of natural logs. However, multiplication inside natural log can be converted to addition outside logarithms through the rule $\ln(ab) = \ln(a) + \ln(b).$

Mistake Example: $\ln(x+2) \rightarrow \ln(x) + \ln(2),$ $\ln(2x) \rightarrow \ln(2)\ln(x),$ $\ln(x^2) \rightarrow \ln(x)^2,$ $\ln(2x) \rightarrow 2\ln(x)$
Detection Rule: Difference expression contains at least one natural log.

The following additional exclusion rules were introduced, based on the empirical results of testing the mistake example cases above:

If Self-Division or Multiplication by Variable or Square Root of Square or Positive or Negative Root has been triggered, exclude Distribution of Multiplication.
If Multiplication by Variable has been triggered, exclude Partial Cancellation within Fraction.

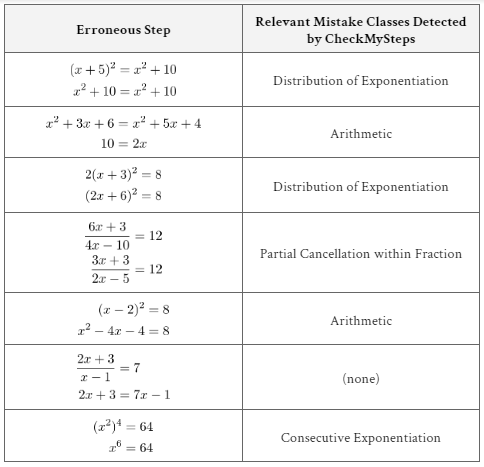
Appendix 3: External Sample of Algebraic Mistakes

The algebraic errors generated by an undergraduate tutor for the purposes of validation are provided in the table below, together with the relevant mistake classes detected by CheckMySteps. In 10 out of the 14 steps, CheckMySteps detected a relevant mistake class and supplied relevant feedback.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.