Building an Iron Man Suit: A Physics Workbook

by Justin Skycak (@justinskycak) on

A workbook I created to explain the math and physics behind an Iron Man suit to a student who was interested in the comics / movies.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Choosing the Right Metal

What metal do we need?

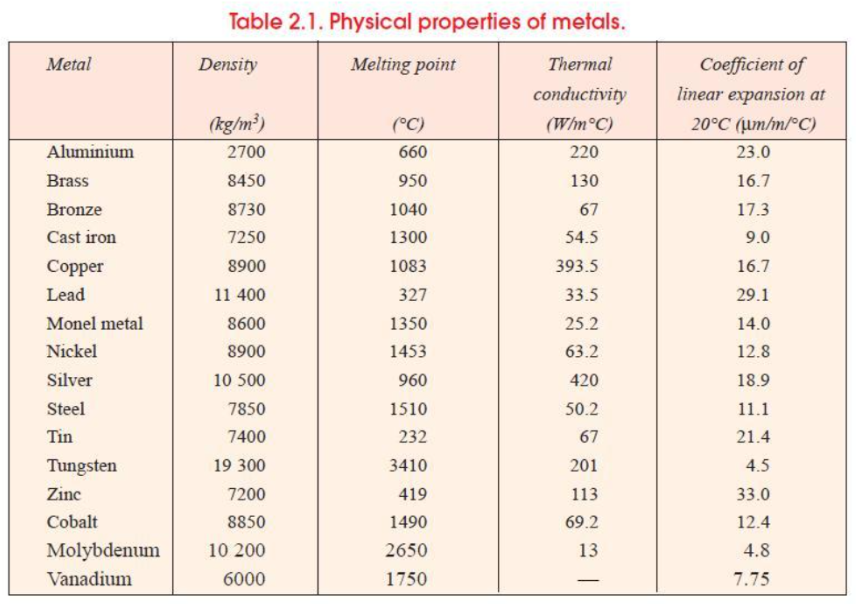
image
Source: A Textbook of Machine Design (2005)


  1. We are looking for a light metal. Let’s compare densities.
  • a. What is the median metal density?
  • b. What is the first quartile metal density?
  • c. Which metals have a density that is less than the first quartile metal density?

  1. We also want a metal that can withstand temperatures up to $1000$ degrees Celsius. Of the metals you listed in 1c, which ones meet this criterion?

  2. Thermal expansion could cause the suit to malfunction at high temperatures. Of the metals you listed in 2, which ones have a coefficient of linear expansion that is less than $10?$

  3. Here are some questions about the metal you chose. If a question is unclear, assume it refers to the question that preceded it.

  • a. Suppose we have $1 \textrm{ m}^3$ of that metal. How many kilograms is this?
  • b. How many $\textrm{cm}^3$ are there in a $\textrm{m}^3?$ (Think about how many $\textrm{cm}$ there are in a $\textrm{m},$ and about how many $\textrm{cm}^2$ there are in a $\textrm{m}^3.$)
  • c. Suppose we have $500 \textrm{ cm}^3$ of that metal. How many kilograms is this?
  • d. What volume of metal would we need to have $10 \textrm{ kg}$ of metal?
  • e. What volume of metal would we need to have $500 \textrm{ kg}$ of metal?
  • f. There are $1,000,000 \textrm{ \mu m}$ in $1 \textrm{ m}.$ What percent of $1 \textrm{ m}$ is $1 \textrm{ \mu m}?$
  • g. If our metal, originally at $20$ degrees Celsius, is heated to $900$ degrees Celsius, by what percent does its length expand? (an increase of $1$ degree Celsius corresponds to the percent length increase you found in question 4f.)
  • h. By what percent does its volume expand?
  • i. By what percent does its density increase?
  • j. If our metal was originally $0.5 \textrm{ m}$ long, what would its new length be?
  • k. If our metal was originally a cube with side length $0.5 \textrm{ m},$ what was its original volume? What is its new volume (after heating)?
  • l. What is the new density?
  • m. Suppose we found a cube of metal at $500$ degrees Celsius with side length $1 \textrm{ m}.$ What would its side length be at $20$ degrees Celsius?
  • n. What would its volume be at $20$ degrees Celsius?
  • o. What would its density be at $20$ degrees Celsius?
  • p. What is its density at $500$ degrees Celsius?
  • q. Suppose we do not want the length of our metal to expand by more than $0.001 \%.$ What is the maximum temperature to which we can heat our metal?

Choosing the Right Paint Ratio

If we’re going to build an Iron Man suit, we’ve got to paint it the right colors. So… let’s figure out a few paint-mixing problems.

image


See that yellow on the mask? We’re going to mix a bit of red paint into yellow paint to make it. For each of the combinations below, calculate the percent of brown paint in the mixture.

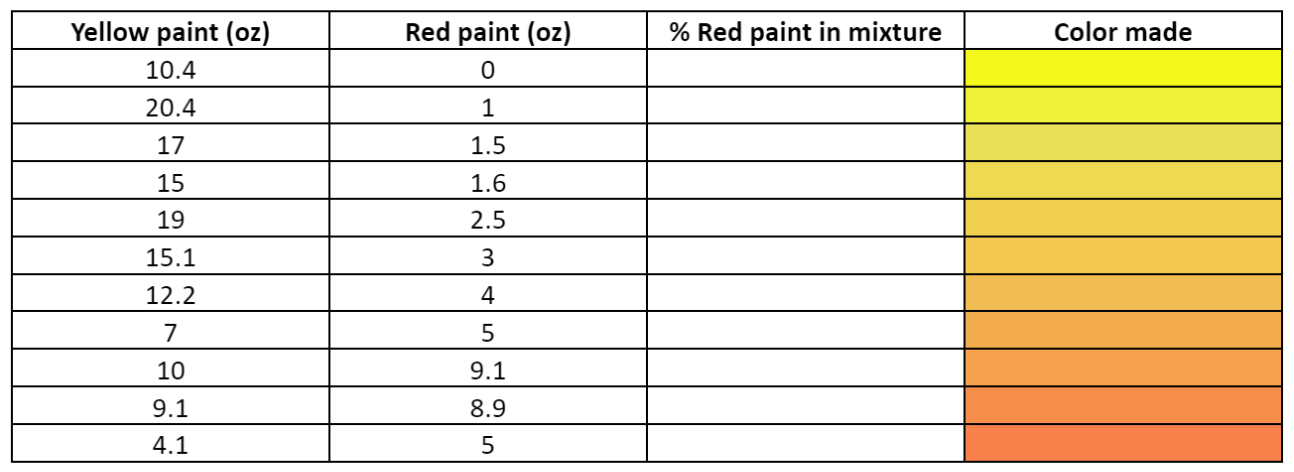
image


  1. What color do you think best matches the mask color?

  2. What percent red paint corresponds to the color you chose?

  3. Suppose we have 16 oz of yellow paint. How many oz of red paint must we mix in to make the color?

  4. Suppose we have 32 oz of yellow paint. How many oz of red paint must we mix in to make the color?

  5. How much of each color should we use if we want to make 16 oz TOTAL of paint?

  6. How much of each color should we use if we want to make 32 oz TOTAL of paint?

  7. How many cups of red paint do we need per cup of yellow paint? (1 cup = 16 oz)

  8. How many cups of yellow paint do we need per cup of red paint?

  9. Suppose we mix 1 cup of red paint with 9 cups of yellow paint. Is this mixture too red or too yellow? How much red or yellow paint should we add to fix the mixture?

  10. Suppose we mix 3 gallons of red paint with 30.1 gallons of yellow paint. Is this mixture too red or too yellow? How much red or yellow paint should we add to fix the mixture?

  11. Suppose we mix 1.5 fishtanks of red paint with 12 fishtanks of yellow paint. Is this mixture too red or too yellow? How much red or yellow paint should we add to fix the mixture?

  12. Suppose we mix 1.7 Pacific Oceans of red paint with 15 Pacific Oceans of yellow paint. Is this mixture too red or too yellow? How much red or yellow paint should we add to fix the mixture?

Ok… We’re almost done…

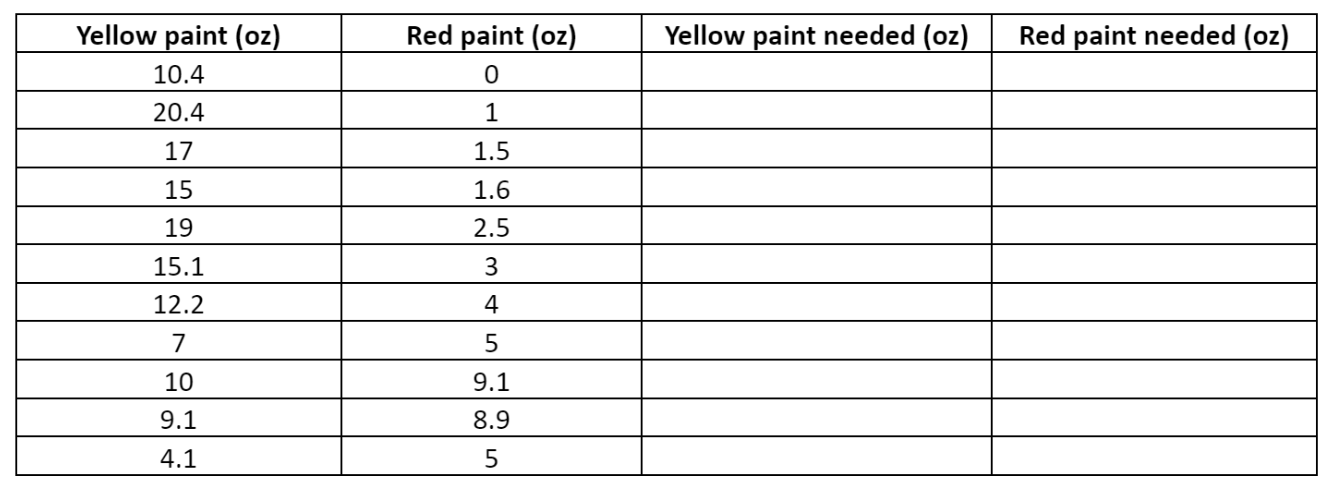
We don’t want to waste paint. How much red paint, or how much yellow paint, must we add to each of the mixtures in the table to turn each mixture into your chosen color?

image


Testing the Suit's Flight Ability

Now, we’re going to test our Iron Man suit’s maximum flight time (from a single thrust).

We’ll use the equation for projectile motion,

$\begin{align*} y(t) = y_0 + v_0 t - \dfrac{g}{2}t^2. \end{align*}$


In this equation:

  • $y(t)$ is the height of the projectile in terms of time $t$
  • $y_0$ is the initial height of the projectile
  • $v_0$ is the initial upward velocity of the projectile
  • $g = 9.81 \textrm{ m/s}^2$ is the acceleration due to gravity near the surface of the Earth
image


Suppose we test our suit from ground level $(y_0 = 0),$ and suppose that our suit can attain an initial upward velocity of $20 \textrm{ m/s}$ off a single thrust $(v_0 = 20).$

  1. What are the zeroes of our quadratic equation?

  2. Which is the nontrivial zero (which zero represents the time we are interested in finding)?

  3. How long does it take before our Iron Man suit hits the ground?

  4. How long does it take before our Iron Man suit reaches its maximum height? (hint: think vertex!)

  5. You should notice something peculiar about your answers to 3 and 4. Why are they related this way? (hint: symmetry!)

  6. What is the range of our function $y(t)?$ Can you write it in interval notation?

  7. For our function to make sense in the context of this test, we need to restrict the range. How should we restrict the range? Can you write this in interval notation? (hint: can we have a negative height in this situation?)

Now, answer the same questions again, this time supposing that we test our suit from the top of a $50 \textrm{ m}$ cliff $(y_0 = 50).$ Assume that the initial upward velocity stays the same and the suit lands at the bottom of the cliff.

  1. What are the zeroes of are quadratic equation?

  2. Which zero makes sense in context of the problem?

  3. How long does it take before our Iron Man suit hits the ground?

  4. How long does it take before our Iron Man suit reaches its maximum height? (hint: think vertex!)

  5. You should notice that the previous two answers are not related in the same fashion as they were when we started at ground level. Why not?

  6. What is the range of our function $y(t)?$ Can you write it in interval notation?

  7. For our function to make sense in the context of this test, we need to restrict the range. How should we restrict the range? Can you write this in interval notation? (hint: again, can we have a negative height in this situation?)

Cutting the Mask

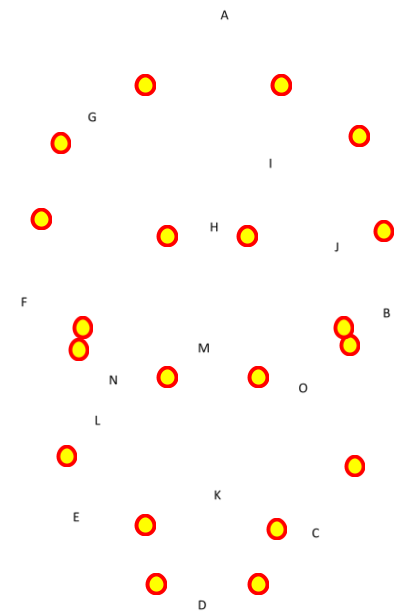
Here we have… THE IRON MAN MASK!

But there’s one problem: how does one turn a drawing of an Iron Man mask into an actual metal copy?

In order to cut the pieces needed for the mask, we have to express the cuts as equations that a computer can follow. For each of the segments/curves in the mask, write an equation that closely follows the cut lines.

Tip: You can code this entire mask only using lines and parabolas.

Tip: Draw gridlines, label points, and then use the points as a guide for your equations.

image



Want to get notified about new posts? Join the mailing list and follow on X/Twitter.