Breadth-First and Depth-First Traversals

by Justin Skycak (x.com/justinskycak) on February 01, 2022

Graphs show up all the time in computer science, so it's important to know how to work with them.

This post is part of the book Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. Suggested citation: Skycak, J. (2022). Breadth-First and Depth-First Traversals. In Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. https://justinmath.com/breadth-first-and-depth-first-traversals/

Want to get notified about new posts? Join the mailing list.

Graphs show up all the time in computer science, so it’s important to know how to work with them. For example, consider the following graph:

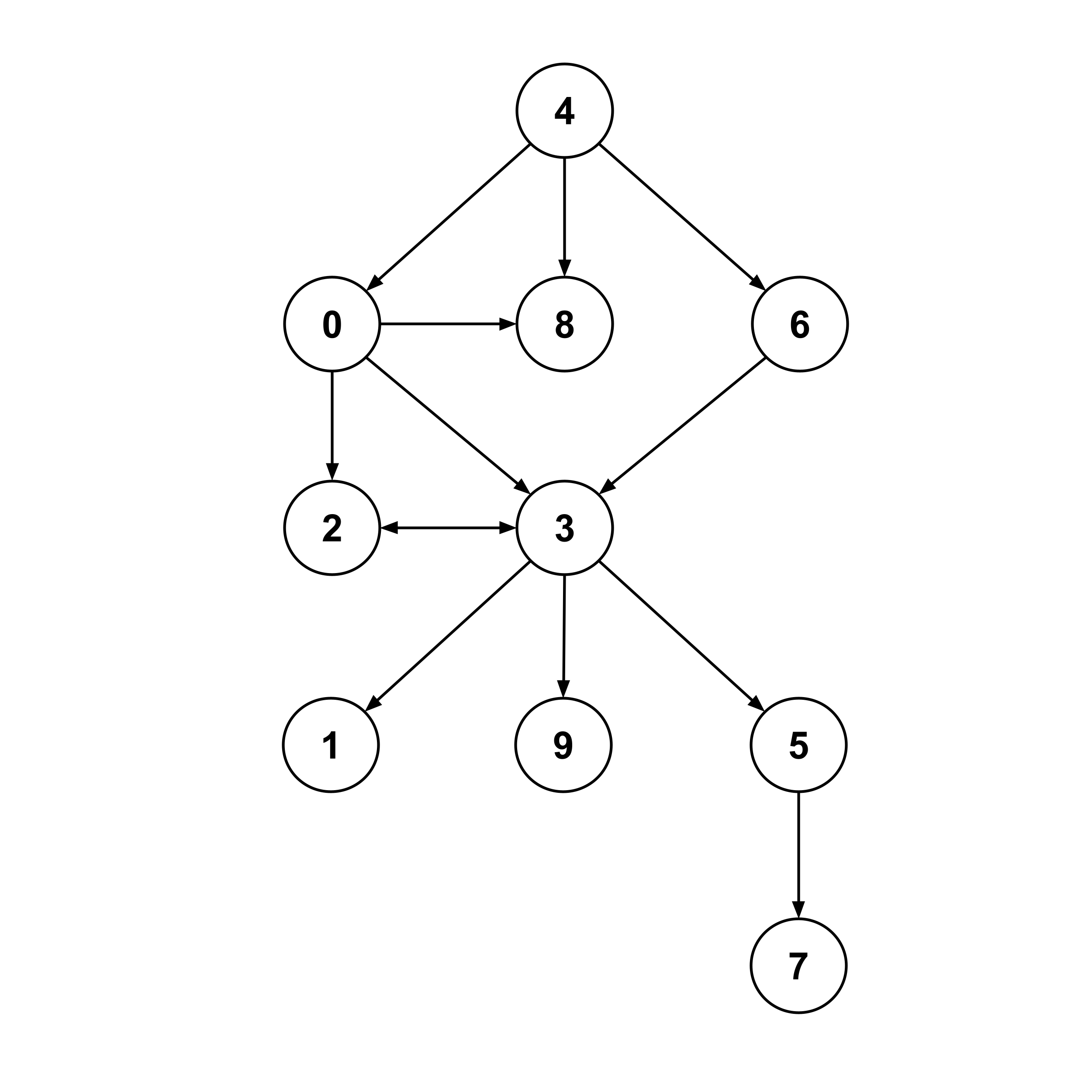
At its core, this graph is just a list of edges. Each edge $(a,b)$ represents a connection from node $a$ to node $b.$


edges = [
    (0,2), (0,3), (0,8),
    (2,3),
    (3,1), (3,2), (3,5), (3,9),
    (4,0), (4,6), (4,8),
    (5,7),
    (6,3)
]

Graph Class

When working with graphs, it’s usually convenient and efficient to parse edges into a Graph class that handles operations behind the scenes.


>>> graph = Graph(edges)

>>> graph.get_child_ids(3)
[1, 2, 9, 5]

>>> graph.get_parent_ids(3)
[0, 2, 6]

>>> graph.get_child_ids(4)
[0, 8, 6]

>>> graph.get_parent_ids(4)
[]

>>> graph.get_child_ids(7)
[]

>>> graph.get_parent_ids(7)
[5]

Breadth-First and Depth-First Traversals

In addition to getting the children or parents of a particular node in the graph, it’s common to need to traverse though the graph in various ways. The two most common types of traversals are breadth first and depth first.

A breadth-first traversal starts at a node and then visits its children, its grandchildren, its great-grandchildren, and so on. Intuitively, it proceeds outward from the root node in broad layers.


>>> graph.get_ids_breadth_first(4)
[4, 0, 8, 6, 2, 3, 1, 9, 5, 7]

# Note: there are other valid breadth-first traversals
# that would also be fine. For example:
[4, 8, 6, 0, 3, 2, 9, 5, 1, 7]

On the other hand, a depth-first traversal goes down the entire family tree of a single child before going down the family tree of another child. Intuitively, it proceeds outward from the root node in deep spikes.


>>> graph.depth_first(4)
[4, 0, 2, 3, 1, 9, 5, 7, 8, 5]

# Note: there are other valid depth-first traversals
# that would also be fine. For example:
[4, 8, 6, 3, 1, 5, 7, 9, 2, 0]

Implementation via Queues and Stacks

Take a moment to make sure you understand the examples above before reading on.

Breadth-first and depth-first traversals are simple to implement using queues and stacks (respectively), which are list-like data structures that follow specific conventions regarding the order in which items can be loaded and unloaded.

In a queue, the first item loaded becomes the first item unloaded (i.e. first-in-first-out, just like a line at the grocery store).
In a stack, the first item loaded becomes the LAST item unloaded (i.e. first-in-last-out, just like a stack of paper).

To generate a breadth-first traversal, the following algorithm can be used:


queue = [rootNode]
visited = {rootNode: True}
traversal = [rootNode]

while queue not empty:
    unload node from queue
    for each child of node:
        if child has not been visited:
            load child to queue and traversal
            record visit

Below is a concrete walkthrough showing how the algorithm above generates a breadth-first traversal from root node 4.


queue = [4], visited = {4:T}, traversal = [4]

unload 4 --> queue = []
- child 0 has not been visited, so visit it
    queue = [0]
    visited = {0:T,4:T}
    traversal = [4,0]
- child 8 has not been visited, so visit it
    queue = [0,8]
    visited = {0:T,4:T,8:T}
    traversal = [4,0,8]
- child 6 has not been visited, so visit it
    queue = [0,8,6]
    visited = {0:T,4:T,6:T,8:T}
    traversal = [4,0,8,6]

unload 0 --> queue = [8,6]
- child 2 has not been visited, so visit it
    queue = [8,6,2]
    visited = {0:T,2:T,4:T,6:T,8:T}
    traversal = [4,0,8,6,2]
- child 3 has not been visited, so visit it
    queue = [8,6,2,3]
    visited = {0:T,2:T,3:T,4:T,6:T,8:T}
    traversal = [4,0,8,6,2,3]

unload 8 --> queue = [6,2,3]
- (no children)

unload 6 --> queue = [2,3]
- child 3 has already been visited, so skip it

unload 2 --> queue = [3]
- (no children)

unload 3 --> queue = []
- child 1 has not been visited, so visit it
    queue = [1]
    visited = {0:T,1:T,2:T,3:T,4:T,6:T,8:T}
    traversal = [4,0,8,6,2,3,1]
- child 9 has not been visited, so visit it
    queue = [1,9]
    visited = {0:T,1:T,2:T,3:T,4:T,6:T,8:T,9:T}
    traversal = [4,0,8,6,2,3,1,9]
- child 5 has not been visited, so visit it
    queue = [1,9,5]
    visited = {0:T,1:T,2:T,3:T,4:T,5:T,6:T,8:T,9:T}
    traversal = [4,0,8,6,2,3,1,9,5]

unload 1 --> queue = [9,5]
- (no children)

unload 9 --> queue = [5]
- (no children)

unload 5 --> queue = []
- child 7 has not been visited, so visit it
    queue = [7]
    visited = {0:T,1:T,2:T,3:T,4:T,5:T,6:T,7:T,8:T,9:T}
    traversal = [4,0,8,6,2,3,1,9,5,7]

unload 7 --> queue = []
- (no children)

queue is empty --> nothing left to unload --> DONE
Final traversal: [4,0,8,6,2,3,1,9,5,7]

Generating a depth-first traversal is almost exactly the same. The only difference is that we use a stack instead of a queue. A concrete example illustrating the difference between a stack and a queue is given below.

With a queue, we load on the right and unload on the left. For example, given a queue [1,2], loading 3 gives [1,2,3]. If we unload, the unloaded element is 1 and the remaining queue is [2,3].
With a stack, we load on the right and unload on the right. For example, given a stack [1,2], loading 3 gives [1,2,3]. If we unload, the unloaded element is 3 and the remaining stack is [1,2].

Time Complexity

Because breadth-first and depth-first traversals both visit each node once and only once, they both have time complexity $O(n)$ where $n$ is the number of nodes in the graph.

Exercises

Implement a Graph class with all the methods described above, and make sure to test it on several different types of graphs. You can use the graph shown here as one of your test cases, but you should also test several significantly different cases (e.g. cycles, an instance of two arrows pointing the opposite way, a disconnected graph, etc).

Want to get notified about new posts? Join the mailing list.