Applications of Calculus: Optimization via Gradient Descent

Calculus can be used to find the parameters that minimize a function.

This post is part of the series Connecting Calculus to the Real World.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

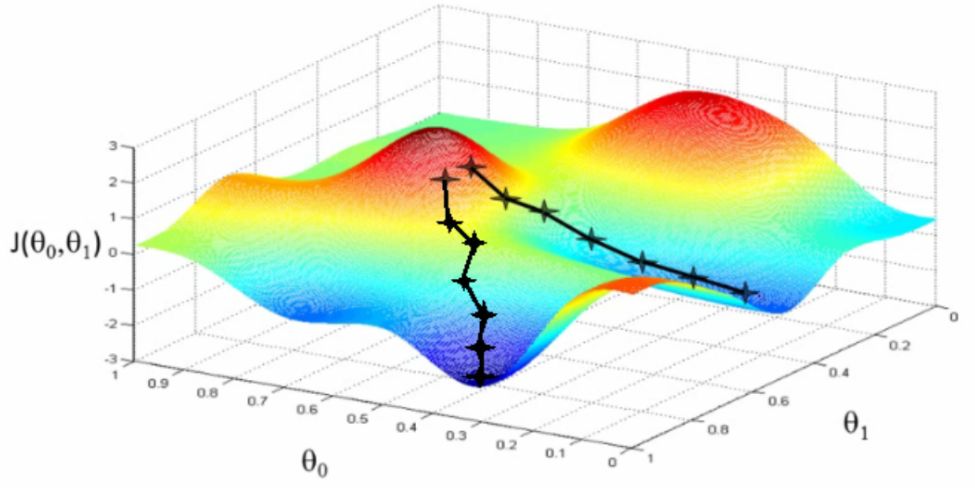
In technology and engineering, we are often faced with the task to optimize some function that represents a system’s performance as a function of the parameters of its components. However, the function to be optimized is often so complicated that you can’t solve it with pencil and paper, and it may even contain too many variables to graph on your computer.

Fortunately, the concept of the derivative makes it possible to optimize many of these equations.

For multivariable functions, the derivative is called the gradient. Optimization problems are normally stated as finding the parameters that minimize a function, and we can use the gradient to “descend” down the landscape of the function into its lowest points. (if you want to maximize instead, you can turn it into a minimization problem by tacking on a negative.)

The method of gradient descent starts with an initial guess at the parameters, which places you somewhere on a “mountain” in the function’s graph. Your goal is to get down from the mountain, into a valley, but there is a heavy fog that makes it impossible to see around you. Since you can’t see where the valley is, you have to figure out how to guess the correct direction to go by looking only at the ground you stand on.

The key is to pay attention to the gradient, or steepness. If you take a step forward and you notice that your forward foot lands higher, then you’re probably going up the mountain, so you shouldn’t continue in that direction. If you take a step forward and your forward foot lands lower, then you’re probably going down the mountain, so you should continue. And if you keep on taking steps down the mountain, you’ll eventually reach the bottom.

This is the method of gradient descent: descend down the path where the gradient is the steepest.

This post is part of the series Connecting Calculus to the Real World.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.