A Visual, Inductive Proof of Sharkovsky’s Theorem

by Justin Skycak (@justinskycak) on January 01, 2015

Many existing proofs are not accessible to young mathematicians or those without experience in the realm of dynamic systems.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

The proof of Sharkovsky’s Theorem for the special case of odd periods, found in Burns and Hasselblatt’s The Sharkovsky Theorem: A Natural and Direct Proof, is presented along with extensive visual diagrams to ease the reading. The special case of Sharkovsky’s Theorem for odd periods is then used to prove the general case of Sharkovsky’s Theorem.

Introduction

Many physical systems can be described mathematically as dynamical systems, objects whose state changes over time according to an update function. It is often useful to know about the periodicity of points in the system as they are iterated by the update function. For example, if a state is mapped back to itself by the update function, then the state is an equilibrium of the network. Similarly, if we know whether a state will eventually map to itself, we can determine whether the system is undergoing a predictable state cycle or its behavior is aperiodic.

A familiar example of a periodic point of a function $f$ is a fixed point, a point $p$ such that $f(p) = p.$ Generally speaking, fixed points of $f$ are periodic points of period $1.$ A periodic point of period $2$ is a point $p$ such that $(f \circ f)(p) = p.$ To ease notation, we denote $f \circ f$ by $f^2.$ Then a periodic point of period $3$ is a point $p$ such that $f^3(p) = p,$ where $f^3$ means $f \circ f \circ f,$ and so on. In general, we have the following definition:

Definition. Let $f$ be a function and let $p$ be a point for which $f^m(p)$ is defined. If $f^m(p) = p,$ then $p$ is a periodic point of period $m$ with respect to $f.$

Unfortunately, there is ambiguity when we speak about the period of a periodic point. If $p$ is a point of period $m$ for $f,$ then $p$ is also a point of period $2m$ because

$\begin{align*} f^{2m}(p) = f^m(f^m(p)) = f^m(p) = p. \end{align*}$

In general, we see that $p$ is a periodic point of period $km$ for any $k \in \mathbb{N}.$ That is, the set of periods of $p$ is a superset of $\lbrace km : k \in \mathbb{N} \rbrace.$ However, if $a \in \mathbb{N}$ is a factor of $m,$ then it is possible (but not necessary) that $p$ is also a point of period $\frac{m}{a}.$ Thus, there may be other periods of $p$ that are not of the form $km.$ This ambiguity is removed by the following definition:

Definition. Suppose that $p$ is a periodic point of period $m$ with respect to a function $f.$ If $p$ has no period that is less than $m,$ then $m$ is the minimal period of $p.$ Accordingly, we say that $p$ is a point of minimal period $m.$

Remark. If the minimal period of $p$ is $m,$ then the set of periods of $m$ is precisely $\lbrace km : k \in \mathbb{N} \rbrace.$

It has long been known that for a continuous function, existence of a periodic point of period $2$ implies existence of a periodic point of period $1$ (a fixed point). This is an immediate consequence of the intermediate value theorem, as will be shown in a later discussion. From later studies (Leibenzon 1953; Coppel 1955; Myshkis, Lepin 1957) of periodic points of continuous functions, it was found that for a continuous function, existence of a point of period greater than two implies existence of a periodic point of period $2$ and thus a fixed point as well (Sharkovsky 2008).

These discoveries of fixed points suggested that there was an ordering $\succ$ of periods for periodic points: if $m > 2,$ then $ m \succ 2 \succ 1.$ Indeed, Ukranian athematician Oleksandr Sharkovsky discovered (Sharkovsky, 1964) the entire ordering, which is now known as the Sharkovsky ordering.

Since Sharkovsky’s discovery, many novel and modified proofs, such as those in (Ho, Morris 1981; Du 2004; Du 2007; Burns, Hasselblatt 2011) of Sharkovsky’s Theorem have emerged. However, many of the proofs are not accessible to young mathematicians or those without experience in the realm of dynamic systems. The goal of this paper is to present a specific case of the proof of Sharkovsky’s Theorem (as found in Burns and Hasselblatt, 2011) in a clear fashion, with extensive use of visual aids. Then, we will use the special case to inductively prove the full Sharkovsky’s Theorem.

Preliminary Lemmas

Before we begin the proof of Sharkovsky’s Theorem, we must introduce some preliminary lemmas and definitions that comprise the foundation of the proof.

Throughout the paper, we will assume that $f$ is a continuous function from one compact interval to another compact interval, and we will assume that $I$ and $J$ are compact intervals.

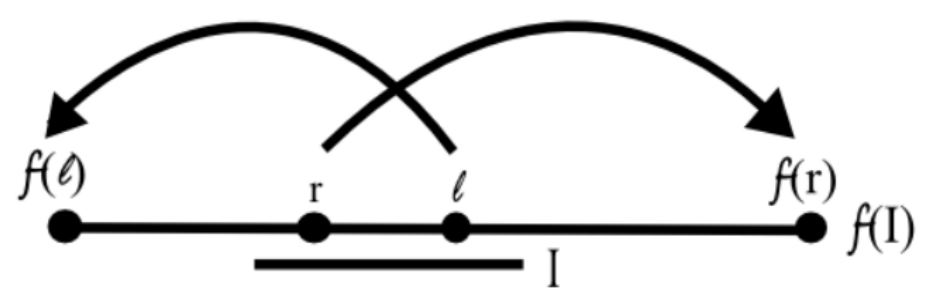
Lemma 1. If $f(I) \supset I,$ then $f$ has a fixed point in $I.$

Proof. Choose $\ell, r \in I$ such that $f(\ell), f(r)$ are, respectively, the left and right endpoints of $f(I).$ We have that $f(\ell) - \ell < 0$ and $f(r) - r > 0,$ so by the intermediate value theorem, there is a point $p \in I$ such that $f(p) - p = 0.$ Thus, $f(p) = p,$ and $p$ is a fixed point of $f$ in $I.$ ■

Definition. If $f(I) \supset J,$ then we write $I \to J.$ If

$\begin{align*} J_0 \to J \to \cdots \to J_{n-1}, \end{align*}$

then we call $( J_i)_{i=0}^{n-1}$ an admissible sequence under $f.$ We call a cyclic admissible sequence

$\begin{align*} J_0 \to J_1 \to \cdots \to J_{n-1} \to J_0 \end{align*}$

an $n$-loop and denote it more compactly by $(\to J_i)_{i=0}^{n-1}.$

Furthermore, if $f(I) = J,$ then we write $I \rightarrowtail J.$ If

$\begin{align*} J_0 \rightarrowtail J_1 \rightarrowtail \cdots \rightarrowtail J_{n-1}, \end{align*}$

then we call $(J_i)_{i=0}^{n-1}$ an exact sequence under $f.$ We call a cyclic exact admissible sequence

$\begin{align*} J_0 \rightarrowtail J_1 \rightarrowtail \cdots \rightarrowtail J_{n-1} \end{align*}$

an exact $n$-loop and denote it more compactly by $(\rightarrowtail J_i)_{i=0}^{n-1}.$

Lemma 2. If $I \to J,$ then there is an interval $K \subset I$ such that $K \rightarrowtail J.$

Proof. To see this, consider the graph of $f$ over $I.$ We seek an arc (a continuous curve) in the graph whose projection onto $f(I)$ is exactly $J.$

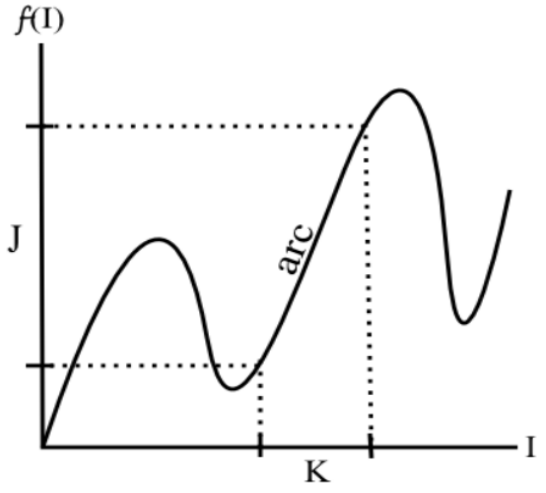
Let $J = [a, b].$ Because $f(I) \supset J,$ we know that the sets $f^{-1}(a)$ and $f^{-1}(b)$ are nonempty, so we can choose

$\begin{align*} x = \inf \left( f^{-1}(a) \cup f^{-1}(b) \right) \end{align*}$

as the leftmost point of $I$ that maps to an endpoint of $J.$

If $x \in f^{-1}(a),$ then we choose

$\begin{align*} y = \inf \lbrace p \in f^{-1}(b) : p > x \rbrace. \end{align*}$

Otherwise, if $x \in f^{-1}(b),$ then we choose

$\begin{align*} y = \inf \lbrace p \in f^{-1}(a): p > x \rbrace. \end{align*}$

Then $y$ is the first point to the right of $x$ that maps to the other (opposite $f(x)$) endpoint of $J.$ Choose $K = [x, y].$ By the intermediate value theorem, then, $f(K) = J.$ ■

Definition. We say that a point $p$ follows the $n$-loop $(\to J_i)_{i=0}^{n-1}$ or the exact $n$-loop $(\rightarrowtail J_i)_{i=0}^{n-1}$ if $f^{i}(p) \in J_i$ for $i = 0,1, \ldots, n-1.$

Lemma 3. If $(\to J_i)_{i=0}^{n-1}$ then there is a periodic point of $f$ that follows the loop.

Proof. By the previous lemma, for $i=0,1,\ldots,n-2$ we can choose a $K_i \subset J_i$ so that $K_i \rightarrowtail J_{i+1},$ and we can choose $K_{n-1} \subset J_{n-1}$ so that $K_{n-1} \rightarrowtail J_0.$

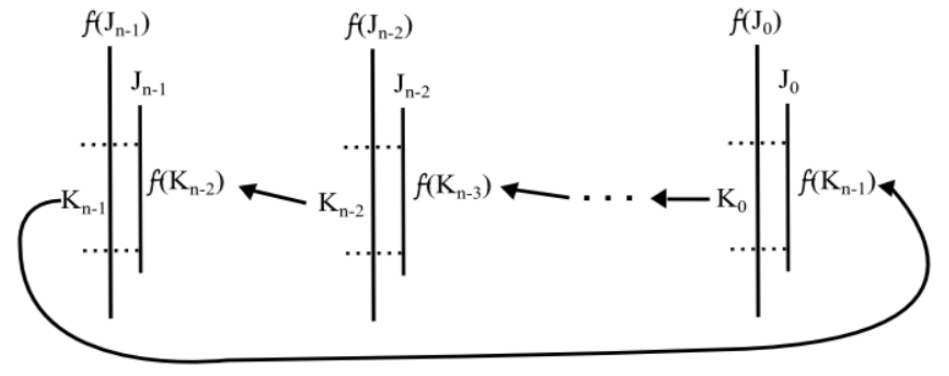
Because $f$ is continuous, we can shrink each interval $K_i$ to an interval $K_i’$ so that $K_i \rightarrowtail K_{i+1}$ for $i = 0,1,\ldots, n-2$ and $K_{n-1} \rightarrowtail K_0.$

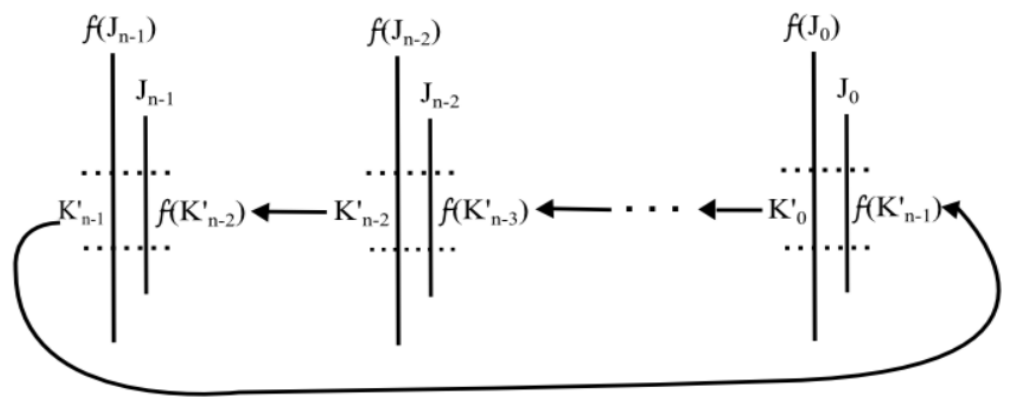
We have that $(\rightarrowtail K_i’)_{i=0}^{n-1}.$ Then $f^n(K_0’) \supset K_0’,$ so by Lemma 1 $f^n$ has a fixed point $p \in K_0’.$ This means $p$ is a periodic point of period $n$ for $f.$ Furthermore, because $(\rightarrowtail K_i’)_{i=0}^{n-1}$ is an exact admissible sequence, $p$ follows the exact $n$-loop $(\rightarrowtail K_i’)_{i=0}^{n-1}.$ ■

Definition. We say that an $n$-loop is elementary if every point that follows it has period $n.$

Corollary 4. For every elementary $n$-loop under $f,$ there is a periodic point of period $n$ that follows the loop.

Proof. This is a direct result from previous definition being applied to Lemma 3. ■

Sharkovsky's Theorem for Odd Periods

Definition. Take the word “odd” to mean

$\begin{align*} 3 \succ 5 \succ 5 \succ 7 \succ \cdots. \end{align*}$

The Sharkovsky ordering is

$\begin{align*} \textrm{odd} \succ 2 \cdot \textrm{odd} \succ 2^2 \cdot \textrm{odd} \succ 2^3 \cdot \textrm{odd} \succ \cdots \succ 2^3 \succ 2^2 \succ 2 \succ 1. \end{align*}$

Theorem 5. Sharkovsky’s Theorem. If $f$ has a periodic point of minimal period $m$ and $m \succ \ell,$ then $f$ has a periodic point of minimal period $\ell.$

We seek to prove the special case of Sharkovsky’s period when $m$ is odd. Our strategy is to find an elementary $\ell$-loop for each $\ell \prec m$ and then apply Corollary 4.

Definition. Let $\mathscr{O}$ be the set of points in an $m$-cycle of $f.$ From this point on, define $I = [p, q]$ where $p$ is the rightmost point of $\mathscr{O}$ such that $f(p) > p$ and $q$ is the point of $\mathscr{O}$ that is immediately right of $p.$ We define $\mathscr{O}_x$ as the set of points of $\mathscr{O}$ that are between $c$ and $x,$ inclusive, and we say that $x \in \mathscr{O}$ switches sides if $x$ and $f(x)$ are on opposite sides of $c.$

We will prove Sharkovsky’s Theorem for odd periods by considering the case when not all points of a cycle switch sides. Whenever a cycle has odd minimal period, it follows that not all points switch sides – otherwise, there would be a smaller minimal period, which is contradictory.

Proposition 6. If an $m$-cycle $\mathscr{O}$ (with $m \geq 2$) contains a point that does not switch sides, then there are elementary $\ell$-loops of $\mathscr{O}$ for each $\ell \prec m.$

Proof. We will first construct a sequence $(x_i)_{i=0}^k$ in $\mathscr{O}$ that “spirals out as fast as possible.” We construct this sequence recursively.

As an initial condition, choose $x_0$ and $x_1$ as endpoints of $I$ so that $f(x_1) \neq x_0.$ This means our starting arrangement is one of the following:

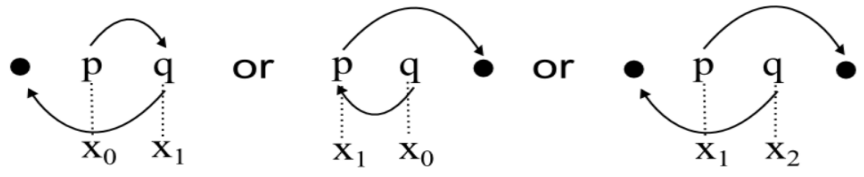
As the recursive step, for $i \geq 1,$ if all points of $\mathscr{O}_{x_i}$ switch sides, then choose $x_{i+1}$ as the point of $f(\mathscr{O}_{x_i})$ that is farthest from $c.$ Otherwise, if some point of $\mathscr{O}_{x_i}$ does not switch sides, the construction terminates and $x_{i+1}$ is defined. An example construction is shown below:

Note that this construction ensures that all the even-indexed terms are on one side of $c$ and all the odd-indexed terms are on the other side.

Lemma 7. Whenever $x_{i+2}$ is defined, $x_{i+2}$ is farther from $c$ than $x_i$ is.

Proof. The case of $i=0$ is clear, so assume $i \geq 1.$ All points of $\mathscr{O}_{x_i}$ and $\mathscr{O}_{x_{i+1}}$ switch sides, so

$\begin{align*} f(\mathscr{O}_{x_i}) \subset f(\mathscr{O}_{x_{i+1}}) \end{align*}$

and

$\begin{align*} f(\mathscr{O}_{x_{i+1}}) \subset f(\mathscr{O}_{x_{i+2}}). \end{align*}$

Then

$\begin{align*} f^2(\mathscr{O}_{x_i}) \subset f(\mathscr{O}_{x_{i+1}}) \subset \mathscr{O}_{x_{i+2}}. \end{align*}$

Since $f$ is one-to-one on $\mathscr{O},$ we have that $\vert \mathscr{O}_{x_{i+2}} \vert \leq \vert \mathscr{O}_{x_i} \vert,$ so our construction necessitates that $\vert x_{i+2} \vert \leq \vert x_i \vert.$ However, we must have $x_{i+1} \neq x_i;$ otherwise, $m$ could not be the minimal period. Thus, $\vert x_{i+2} \vert > \vert x_i \vert.$ ■

Corollary 8. The points of $(x_i)_{i \geq 1}$ are all distinct, and thus the sequence terminates with $x_k$ for some $k \leq m - 1.$

Proof. This is a direct result from the previous lemma. ■

Definition. We say that $J$ is an $\mathscr{O}$-interval if its endpoints are points of $\mathscr{O}.$

Our goal is to construct a sequence $(J_i)_{i=1}^k$ of $\mathscr{O}$-intervals having an $\ell$-loop for each $\ell \prec k,$ and then shrink the intervals to make the loops elementary. Then, we can apply Corollary 4, and we will be finished.

Note that finding an $\ell$-loop for each $\ell \prec k$ is equivalent to finding a $1$-loop and an $\ell$-loop for each even $\ell \leq k$ and for each $\ell \geq k + 2.$

We construct the sequence $(J_i)_{i=1}^k$ as follows: for $1 \leq i \leq k$ and choose $J_i$ as the shortest $\mathscr{O}$-interval that contains $\mathscr{O}_{x_i} \cup I.$ Then $J_1 = I$ and, by Lemma 7, $J_{k-1} \supset J_{k-3} \supset \cdots$ and $J_{k-2} \supset J_{k-4} \supset \cdots.$

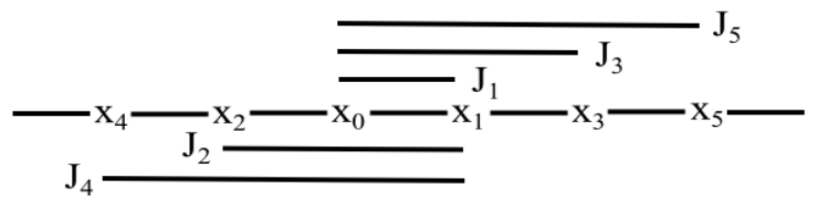
Lemma 9. With our choices of $J_i,$ we have that

(1) $J_1 \to I,$

(2) $J_i \to J_{i+1}$ for $1 \leq i \leq k-1,$ and

(3) $J_k \to J_{k+1}.$

Proof.

(1) $J_1 = I.$

(2) Let $I_i = [x_0, f^{-1}(x_i)]$ or $[f^{-1}(x_i), x_1]$ as appropriate. Then $f(I_i) = J_{i+1}.$ But $J_i \supset I_i,$ so $f(J_i) = J_{i+1}.$

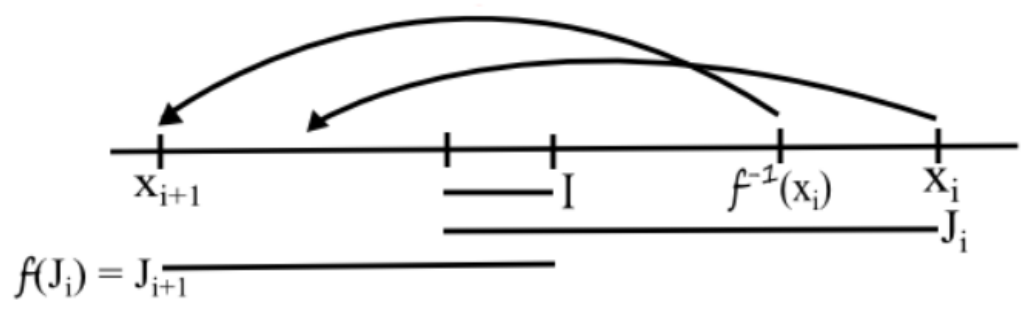
(3) Since $\mathscr{O}_{x_{k-2}} \subset \mathscr{O}_{x_k},$ we have that $f^{-1}(x_{k-2}) \in J_k.$ Because $x_k$ is defined, we know $f^{-1}(x_{k-2})$ switches sides and maps to $x_{k-2}.$ But because the sequence terminates at $x_k,$ we have that $x_k$ does not switch sides. Then $f(J_k)$ contains both $x_{k-1}$ and $f(x_k),$ which are on opposite sides of $c.$

■

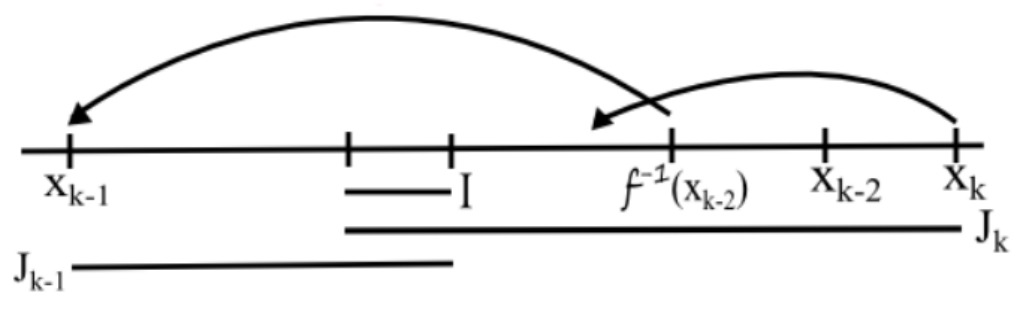
For $0 \leq i \leq k-1,$ we shrink $J_i$ to $I_i$ as in the proof of (2) in the previous lemma. We choose $I_k$ as $[f^{-1}(x_{k-2}), x_k]$ or $[x_k, f^{-1}(x_{k-2})]$ as appropriate.

Then $I_i \subset J_i$ for $1 \leq i \leq k$ and $I_1 = J_1 = I.$

Lemma 10. With our choices of $I_i,$ we have that

(1’) $f(I_1) \supset J_1 = I_1,$

(2’) $f(I_i) \supset J_{i+1} = I_{i+1},$ and

(3’) $f(I_k) \supset J_{k+1} \supset I_{i+1}.$

Proof. The previous arguments for (1), (2), and (3) can be used to prove (1’), (2’), and (3’). ■

Note that $I_i \cap \textrm{Int}(I_k) = \emptyset$ for $1 \leq i \leq k-1.$ Also note that $f(I_k)$ contains $I$ and all intervals on the opposite side of $I.$

(1’), (2’), and (3’) can be summarized by the following diagram:

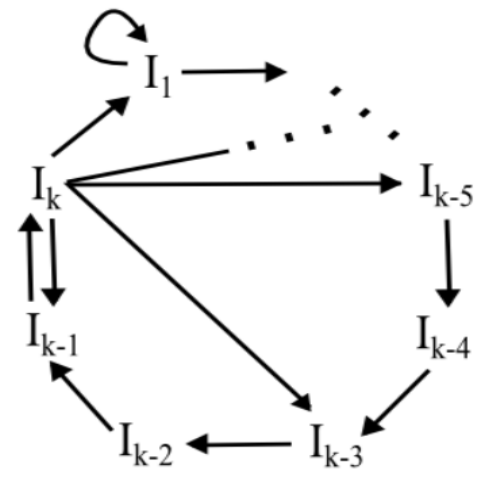
We see that we have several loops:

(A) $I_1 \to I_1$

(B) $I_k \to I_{k - \ell + 1} \to I_{k - \ell + 2} \to$ $\cdots$ $\to I_{k - 1} \to I_k$ for even $\ell \leq k.$

(C) $I_k \to I_1 \to I_1 \to$ $\cdots$ $\to I_1 \to I_2 \to I_3 \to$ $\cdots$ $\to I_{k-1} \to I_k$ with arbitrarily many (say, $j$) occurrences of $I_1$

Lemma 11. A loop $(\to J_i)_{i=0}^{n-1}$ of $\mathscr{O}$-intervals is elementary if it is not followed by any point of $\mathscr{O}$ and $Int(J_0)$ is disjoint from each of $J_1, \ldots, J_{n-1}.$

Proof. Suppose that $p$ is a point that follows the loop. We know that $p \notin \mathscr{O},$ so $p \in \textrm{Int}(J_0).$ But for $1 \leq i \leq n-1$ we have $f^i(p) \notin \textrm{Int}(J_0),$ so $f^i(p) \neq p.$ Thus, $p$ has period $n.$ Therefore, the loop is elementary. ■

Recall that we’ve already shown that $\textrm{Int}(J_k)$ is disjoint from the others. Thus, to prove that the loops (A), (B), and (C) are elementary, we need only show that they cannot be followed by any point of $\mathscr{O}.$

Indeed, (A) has length $1 < m,$ and (B) has length $\ell \leq k \leq m - 1,$ so neither (A) nor (B) can be followed by a point of $\mathscr{O}.$

Loop (C) is slightly more complicated. When $j=1,$ (C) has length $k \leq m-1.$ When $j=2$ and $k \leq m-2,$ (C) has length $k+1 \leq m-1.$ When $j>2,$ (C) has at least $3$ repetitions of $I_1,$ but there are only $2$ points of $\mathscr{O}$ in any $\mathscr{O}$-interval, so (C) cannot be followed by a point of $\mathscr{O}.$

The single case we have left open is when $j = 2$ and $k \geq m - 1.$ However in this case, (C) has length $m,$ and we already know that each point of the $\mathscr{O}$-cycle is a periodic point with period $m.$

(A) has length $1,$ (B) can be made to have any even length $\ell \leq k,$ and (C) can be made to have all lengths $\ell \geq k$ except possibly $m$ itself. Furthermore, (A), (B), and (C) are all elementary loops. Thus, there are elementary loops for each $\ell \prec m.$ ■

However, note that our proof has yielded periods beyond those specified by Sharkovsky’s Theorem. We’ve proven the following extension of Sharkovsky’s Theorem for odd periods:

Theorem 12. (Extension of Sharkovsky’s Theorem for Odd Periods). Suppose that $f$ has a periodic point of minimal period $m.$ Then $f$ has periodic points with the following periods: $1,$ every even $\ell < m,$ and every $\ell \geq m.$

In the next section, we use the extension of Sharkovsky’s Theorem for odd periods to prove Sharkovsky’s Theorem for all periods.

Sharkovsky's Theorem: The General Case

Because every even number can be expressed as the product of a power of $2$ and an odd number, we can prove Sharkovsky’s Theorem for even periods by proving the following:

Theorem 13. Suppose that $f$ has a periodic point of minimal period $2^k m,$ where $m$ is odd, and $\ell \prec 2^k m,$ then $f$ has a periodic point of minimal period $\ell.$

Proof. We use the following lemma to prove the theorem.

Lemma 14. Suppose that $p$ is a point of minimal period $m$ for $f^2.$ Then there is a point of minimal period $2m$ for $f.$ Furthermore, $f$ has a point of period $1.$

Proof. We break the first part of the proof into two cases.

(Case 1) Suppose that $m$ is odd. We know that $p$ has a minimal period of either $m$ or $2m$ under $f.$ If $p$ has a minimal period of $2m$ under $f,$ then the case is proven. Alternatively, if $p$ has a minimal period of $m$ under $f,$ then by Sharkovsky’s Theorem for odd periods we know that there is another point with minimal period $2m$ under $f.$

(Case 2) Suppose that $m$ is even. Suppose, seeking contradiction, that the minimal period of $p$ under $f$ is $m.$ Because $m$ is even, we know that $m = 2j$ for some $j \in \mathbb{N}.$ Since $f^m(p) = p,$ we have that $f^{2j}(p) = p.$ But this means $(f^2)^j(p) = p,$ so the minimal period of $p$ under $f^2$ is at most $j.$ But $j < m,$ and we know that $p$ has minimal period $m$ for $f^2.$ We’ve reached contradiction; $p$ cannot have minimal period $m$ under $f.$ Thus, $p$ has minimal period $m$ under $f.$

By Sharkovsky’s Theorem for odd periods, we know that $f^2$ has a point of minimal period $1,$ so $f$ has a point, say $x,$ of minimal period $2.$ Let $I$ be the interval with endpoints $x$ and $f(x).$ Then $f(I) \supset I,$ so $f$ has a fixed point in $I.$ Thus, $f$ also has a point of period $1.$ ■

Lemma 15. Suppose that $p$ is a point of minimal period $2m,$ where $m$ is odd, for $f.$ Then $f$ has a point of minimal period $\ell$ for each $\ell \prec 2m.$

Proof. We know that $f^2$ has a point of odd minimal period $m.$ Applying the extension of Sharkovsky’s Theorem for odd periods, we have that $f^2$ has points with minimal period $1,$ every even $\ell < m,$ and every $\ell \geq m.$ By the Lemma 14, then, $f$ has points with minimal period $1, 2,$ every $\ell < 2m$ such that $\ell \textrm{ mod } 4 = 0,$ and every even $\ell \geq 2m.$ ■

Theorem 13 is a direct result of repeated application of Lemma 15. Hence, Sharkovsky’s Theorem is proven. ■

Acknowledgements

I thank Professor Jeffrey Diller for introducing me to Sharkovsky’s Theorem and discussing the intracies of its proof with me.

References

Burns, K., Hasselblatt, B.: The Sharkovsky Theorem: A Natural Direct Proof. The American Mathematical Monthly 118(3), 229-244 (2011).

Coppel, W.A.: The solution of equations by iteration, Proc. Cambridge Philos. 51, 41-43 (1955).

Du, B.S.: A simple proof of Sharkovsky’s theorem. Amer. Math. Monthly, 111, 595-599 (2004).

Du, B.S.: A simple proof of Sharkovsky’s theorem revisited. Amer. Math. Monthly, 114, 152-155 (2007).

Ho, Chung Wu; Morris, Charles. A graph-theoretic proof of Sharkovsky’s theorem on the periodic points of continuous functions. Pacific J. Math., 96(2), 361-370 (1981).

Leibenzon, Z.L.: Investigation of certain properties of a continuous point transformation of an interval onto itself which have application in the theory of nonlinear oscillations (in Russian), Akad. Nauk SSSR, Prikl. Mat. Meh. 17, 351-360 (1953).

Myshkis, A.D., Lepin, A.Ya.: Existence of an invariant set, consisting of two points, for certain continuos maps of an interval into itself (in Russian), Uchen. Zap. Belorus. Univ., Ser. Fiz.-Mat. 32, 29-32 (1957).

Sharkovsky, A.N.: Coexistence of cycles of continuous mapping of the line into itself. Ukrainian Math. J., 16, 61-71 (1964).

Sharkovsky, A.N.: Sharkovsky ordering. Scholarpedia, 3(5), 1680 (2008).

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.