A Game-Theoretic Analysis of Social Distancing During Epidemics

by Justin Skycak (@justinskycak) on May 01, 2016

In a simplified problem framing, we investigate the (game-theoretical) usefulness of limiting the number of social connections per person.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

In a simplified problem framing, we investigate the improvement of homogeneous maximization over the maxmin strategy, i.e. the (game-theoretical) usefulness of limiting the number of social connections per person.

Problem Statement

Suppose that there is a contagious delayed-onset fatal disease on a social network. Each person is either susceptible or immune, and biostatisticians are able to infer the prior probability $0 < p < 1$ of immunity and update it to

$\begin{align*} p_{\delta} = \dfrac{p}{1 - \delta} \end{align*}$

as the fractional death toll $\delta$ of the population grows. (In the rest of the paper we will assume that $0 < p_{\delta} < 1.$) Although the biostatisticians may share this information with the public, immunity tests are not commercially available, so no agent knows its type or any other agent’s type.

In response to epidemics, people often engage in social distancing, in which they avoid exposure to disease by avoiding physical contact with others. However, although complete isolation guarantees safety from exposure, people rarely isolate themselves completely because they value not only their health but also their economic interactions and contact with family and friends.

How many social ties should health officials advise people to keep, and how much improvement will their advice (assuming that people follow it) offer over the result that will occur if they do not offer any advice?

Game Setup

In the social network, each node (person) controls its number $k \geq 0$ of connections (physical contacts) with others. Its health is given by $h \in \lbrace 0, 1 \rbrace,$ where $h = 1$ if it survives the epidemic and $h = 0$ if not. A node’s utility is given by

$\begin{align*} u = h f_{\lambda} (k) \end{align*}$

where

$\begin{align*} f_{\lambda}(k) = \begin{cases} k & k \leq \lambda \\ \lambda & k > \lambda \end{cases} \end{align*}$

represents a node’s value of social connections as a linear function which is thresholded at $\lambda > 0.$

The expected utility of a node playing strategy $k$ (i.e. a node with $k$ connections) is

$\begin{align*} u(k) = h(k) f(k), \end{align*}$

where

$\begin{align*} h(k) = E(h \vert k) \end{align*}$

is the expected health, or equivalently, the probability of survival. We will assume that health officials advise nodes to make the number of connections that would maximize utility on a homogeneous network, while in the absence of advice, each node would play the maxmin strategy.

No Advice: Maxmin

Lemma 1. Let $k_m$ be the maxmin strategy. Then

$\begin{align*} f'(k_m) = \ln(1/p_{\delta}) f_{\lambda}(k_m). \end{align*}$

Proof. In the worst case, when a player’s neighbors have links to everyone else, each neighbor will be infected unless it is immune. In this worst case, the expected health of a player with $k$ social ties is $p_{\delta}^k,$ so the expected utility is $p_{\delta}^k f_{\lambda}(k).$ Differentiating, we have

$\begin{align*} \frac{d}{dk} \left[ p_{\delta}^k f_{\lambda}(k) \right] = p_{\delta}^k \left[ f_{\lambda}'(k) + \ln(p_{\delta}) f_{\lambda}(k) \right]. \end{align*}$

Since $p_{\delta} > 0,$ if $k = k_m$ maximizes the worst-case payoff, then

$\begin{align*} f'(k_m) &= -\ln(p_{\delta}) f_{\lambda}(k) \\ &= \ln(1/p_{\delta}) f_{\lambda}(k). \end{align*}$

■

Proposition 2. The maxmin strategy is given by

$\begin{align*} k_m = \dfrac{1}{\ln(1/p_{\delta})} \leq \lambda. \end{align*}$

Proof. If $k_m > \lambda,$ then to have $f_{\lambda}’(k_m) = \ln(1/p_{\delta}) f_{\lambda}(k)$ would require $p_{\delta} = 1$ or $\lambda = 0,$ a contradiction. Hence $k_m \leq \lambda.$ Then $f_{\lambda}(k_m) = k_m$ and $f_{\lambda}’(k_m) = 1,$ so $1 = \ln(1/p_{\delta}) k_m.$ ■

Proposition 2. If all players play a strategy $k,$ then $h(k)$ can be linearly approximated by

$\begin{align*} \hat{h}(k) := \begin{cases} 1 - \left( \frac{1 - p_{\delta}}{\eta} \right) & k \leq \eta \\ p_{\delta} & k > \eta, \end{cases} \end{align*}$

where $5 \lesssim \eta \lesssim 10.$

Proof. Since

$\begin{align*} P(\textrm{infected}) = P(\textrm{not immune}) P(\textrm{some neighbor infected}), \end{align*}$

we have

$\begin{align*} 1 - h(k) = (1 - p_{\delta})(1 - h(k)^k). \end{align*}$

Then $h(k) \geq p_{\delta}$ with near-equality whenever $k$ is not very small ($5 \lesssim \eta \lesssim 10$ for a numerically reasonable cutoff $\eta$). Noting that $h(0) = 1$ (isolation prevents exposure), we use linear approximation between the two points $(0,1),(\eta,p_{\delta})$ of the form $(k,h(k)).$ ■

Remark. The approximation takes advantage of a network effect: if each node has more than a few $(\eta)$ connections, then each node’s chance of infection is nearly as large as if it were connected to every other node in the network.

Proposition 4. If all players play the maxmin strategy $k_m$ and the expected utility is approximated by

$\begin{align*} \hat{u}(k) := \hat{h}(k) f_{\lambda}(k), \end{align*}$

then

$\begin{align*} \hat{u}(k_m) := \begin{cases} \left( 1 - \frac{1 - p_{\delta}}{\eta \ln(1/p_{\delta})} \right) \frac{1}{\ln(1/p_{\delta})} & p_{\delta} \leq e^{-1/\eta} \\ \frac{p_{\delta}}{\ln(1/p_{\delta})} & p_{\delta} > e^{-1/\eta}. \end{cases} \end{align*}$

(Using $5 \lesssim \eta \lesssim 10$ we have $0.8 \lesssim e^{-1/\eta} \lesssim 0.9.$)

Proof. Recall that $k_m = \frac{1}{\ln(1/p_{\delta})} \leq \lambda.$ Substituting $k_m = \frac{1}{\ln(1/p_{\delta})}$ in the expression for $\hat{h}(k_m)$ in Proposition 3 and multiplying by $f(k_m) = k_m = \frac{1}{\ln(1/p_{\delta})}$ yields the conclusion. ■

Advice: Homogeneous Maximization

Lemma 5. If $k$ maximizes $u$ given some belief about others’ strategies and

$\begin{align*} \min \lbrace \eta, \lambda \rbrace \leq k \leq \max \lbrace \eta, \lambda \rbrace, \end{align*}$

then $k = \lambda.$

Proof. We check three cases:

If $\min \lbrace \eta, \lambda \rbrace = \max \lbrace \eta, \lambda \rbrace,$ then $k = \lambda = \eta.$
If $\eta < \lambda,$ then $u$ is increasing on $[\eta,\lambda]$ because $h$ is (to good approximation) constant and $f$ is increasing.
If $\lambda < \eta,$ then $u$ is decreasing on $[\lambda, \eta]$ because $h$ is decreasing and $f$ is constant.

■

Lemma 6. If $k$ maximizes $u$ given some belief about others’ strategies and $k \geq \max \lbrace \eta, \lambda \rbrace,$ then $k = \lambda.$

Proof: For $k \geq \max \lbrace \eta, \lambda \rbrace,$ $f$ is constant; although $h$ is nearly constant, it is still strictly decreasing (albeit asymptotically to $p_\delta$). Consequently, if $k \geq \max \lbrace \eta, \lambda \rbrace,$ then $u(k)$ is maximized at $k = \lambda.$ ■

Proposition 7. If $k$ maximizes $u$ given some belief about others’ strategies, then $k \leq \lambda.$

Proof. From Lemmas 5 and 6, we know that if $k$ maximizes $u$ given some belief about others’ strategies and $k \geq \min\lbrace \eta, \lambda \rbrace,$ then $k = \lambda.$ The result follows. ■

Proposition 8. The homogeneous maximization strategy $\hat{k_M}$ with respect to $\hat{u}$ is given by

$\begin{align*} \hat{k_M} = \dfrac{\eta}{2(1 - p_\delta)} \leq \eta, \end{align*}$

provided that $p_\delta \leq \frac{1}{2}.$

Proof. From Proposition 7 we know that $\hat{k_M} \leq \lambda.$ Consequently, $\hat{u}(k)$ need only be maximized on $0 \leq k \leq \lambda.$ When $k \leq \lambda$ we have $f(k) = k,$ so $\hat{u}(k) = \hat{h}(k)k,$ and thus

$\begin{align*} \hat{u}'(k) &= \hat{h}'(k)k + \hat{h}(k) \\[5pt] &= \begin{cases} 1 - 2 \left( \frac{1 - p_\delta}{\eta} \right) k & k \leq \eta \\ p_\delta & k > \eta. \end{cases} \end{align*}$

We require $\hat{u}’(\hat{k_M}) = 0,$ but $p_\delta > 0,$ so we must have $\hat{k_M} \leq \eta$ with $0 = 1 - 2 \left( \frac{1 - p_\delta}{\eta} \right) k.$ Then $\hat{k_M} = \frac{\eta}{2(1 - p_\delta)} \leq \eta.$ Since $\frac{\eta}{2(1 - p_\delta)} \leq \eta,$ we must have $p_\delta \leq \frac{1}{2}.$ ■

Proposition 9. If all players play $\hat{k_M},$ then the approximate utility is given by

$\begin{align*} \hat{u}( \hat{k_M} ) = \dfrac{\eta}{4(1 - p_\delta)} \end{align*}$

provided $p_\delta \leq \frac{1}{2}.$

Proof. Recall that

$\begin{align*} \hat{k_M} = \dfrac{\eta}{2(1 - p_\delta)} \leq \eta, \lambda \end{align*}$

provided that $p_\delta \leq \frac{1}{2}.$ Then

$\begin{align*} f(\hat{k_M}) = \hat{k_M} = \dfrac{\eta}{2(1 - p_\delta)} \end{align*}$

and

$\begin{align*} \hat{h}(\hat{k_M}) = 1 - \left( \dfrac{1 - p_\delta}{\eta} \right) \hat{k_M} = \dfrac{1}{2}. \end{align*}$

■

Usefulness of Advice

Below are plots of $\hat{k_M}$ (upper) and $k_m$ (lower) for $0 < p_\delta \leq 0.5,$ using $\eta = 7.5.$

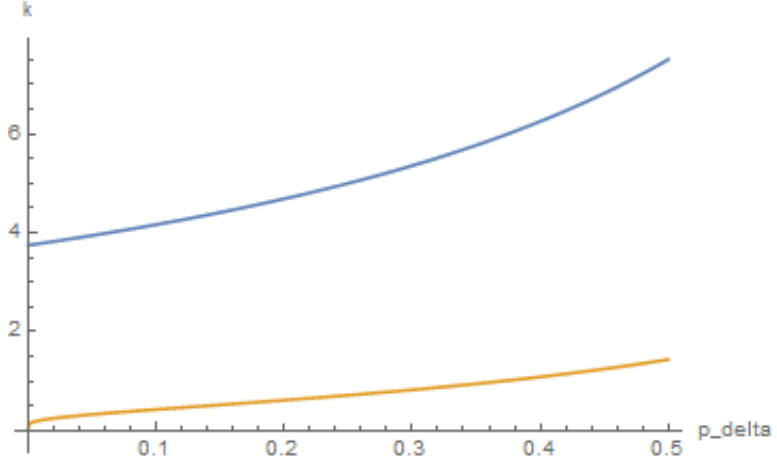
While the maxmin strategy encourages near-isolation as $p_\delta$ becomes small, the homogeneous maximization strategy always permits several connections.

Below are plots of $\hat{u}(\hat{k_M})$ (upper) and $\hat{u}(k_m)$ (lower) for $0 < p_\delta \leq 0.5,$ using $\eta = 7.5.$

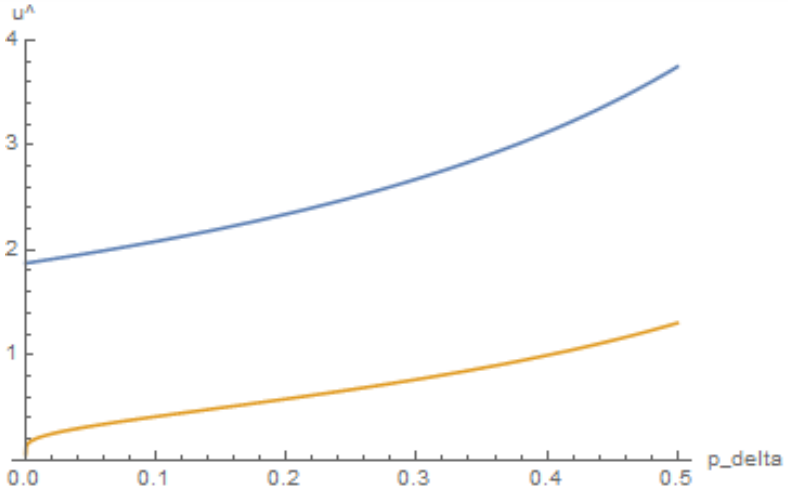
The maxmin strategy’s payoff vanishes as $p_\delta \to 0,$ while the homogeneous maximization strategy’s payoff is roughly maintained.

Below is a plot of $\dfrac{\hat{u}(\hat{k_M})}{\hat{u}(k_m)}$ for $0 < p_\delta \leq 0.5,$ using $\eta = 7.5.$

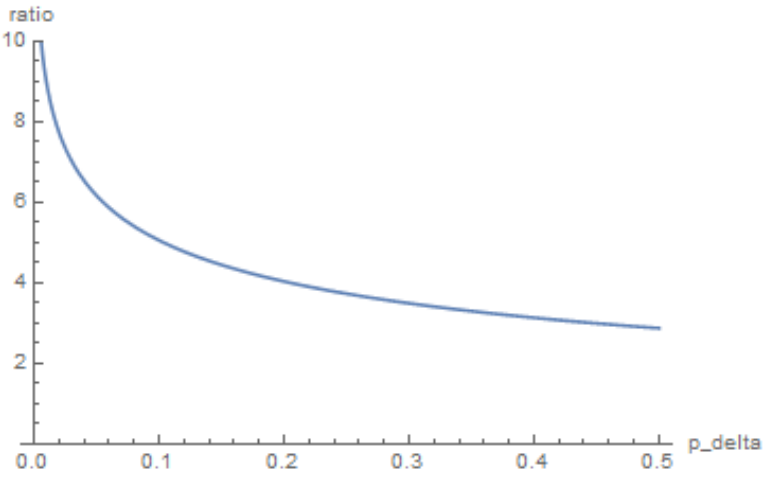
We see that the improvement of homogeneous maximization over maxmin becomes exponentially larger as the probability of immunity becomes smaller. Hence, advice is useful, and extremely useful when very few people are immune to the disease.

Future Work & Comparison to Other Models

Using a differential game theory model, Reluga (2010) found that social distancing is most useful for moderately transmissible diseases. It my model, it was assumed that transmission across social links was certain. It would be interesting to include a variable transmission probability in my model.

Maharaj and Kleczkowski (2012) studied an SIR (spread-infect-recover) model in which decreasing social links resulted in an economic cost. It would be interesting to extend my model to nonfatal diseases and compare results.

Read, Earnes, and Edmunds (2008) investigated the different forms of social contact and suggested that epidemiological models of close contact infection diseases ought to focus on stable social connections, while epidemics of casual contact transmission are well-modeled by random mixing. My model assumes that all social connections are stable. It would be interesting to extend my model to include random mixing as well.

One last idea is to have nodes represent families rather than individuals. Families tend to have close contact ties, and it is unlikely that they would separate in any epidemic. This could plausibly be accomplished by assigning each node a number which represents the number of people in the family. The question would then be whether families should choose a set number of ties with other families, or whether families should limit the total number of family members of the families with which they interact.

References

[1] Reluga, T. C. (2010). Game theory of social distancing in response to an epidemic.

[2] Maharaj, S., & Kleczkowski, A. (2012). Controlling epidemic spread by social distancing: Do it well or not at all. BMC public health, 12(1), 679.

[3] Read, J. M., Eames, K. T., & Edmunds, W. J. (2008). Dynamic social networks and the implications for the spread of infectious disease. Journal of The Royal Society Interface, 5(26), 1001-1007.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.