Trigonometric Functions

Trigonometric functions represent the relationship between sides and angles in right triangles.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Trigonometric Functions. In Justin Math: Algebra. https://justinmath.com/trigonometric-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Trigonometric functions represent the relationship between sides and angles in right triangles.

There are three main “trig” functions: sine, cosine, and tangent, and a mnemonic often used to remember what they represent is SohCahToa:

• • The SINE of an angle is the ratio of the lengths of the OPPOSITE side and the HYPOTENUSE.
• • The COSINE of an angle is the ratio of the lengths of the ADJACENT side and the HYPOTENUSE.
• • The TANGENT of an angle is the ratio of the lengths of the OPPOSITE side and the ADJACENT side.

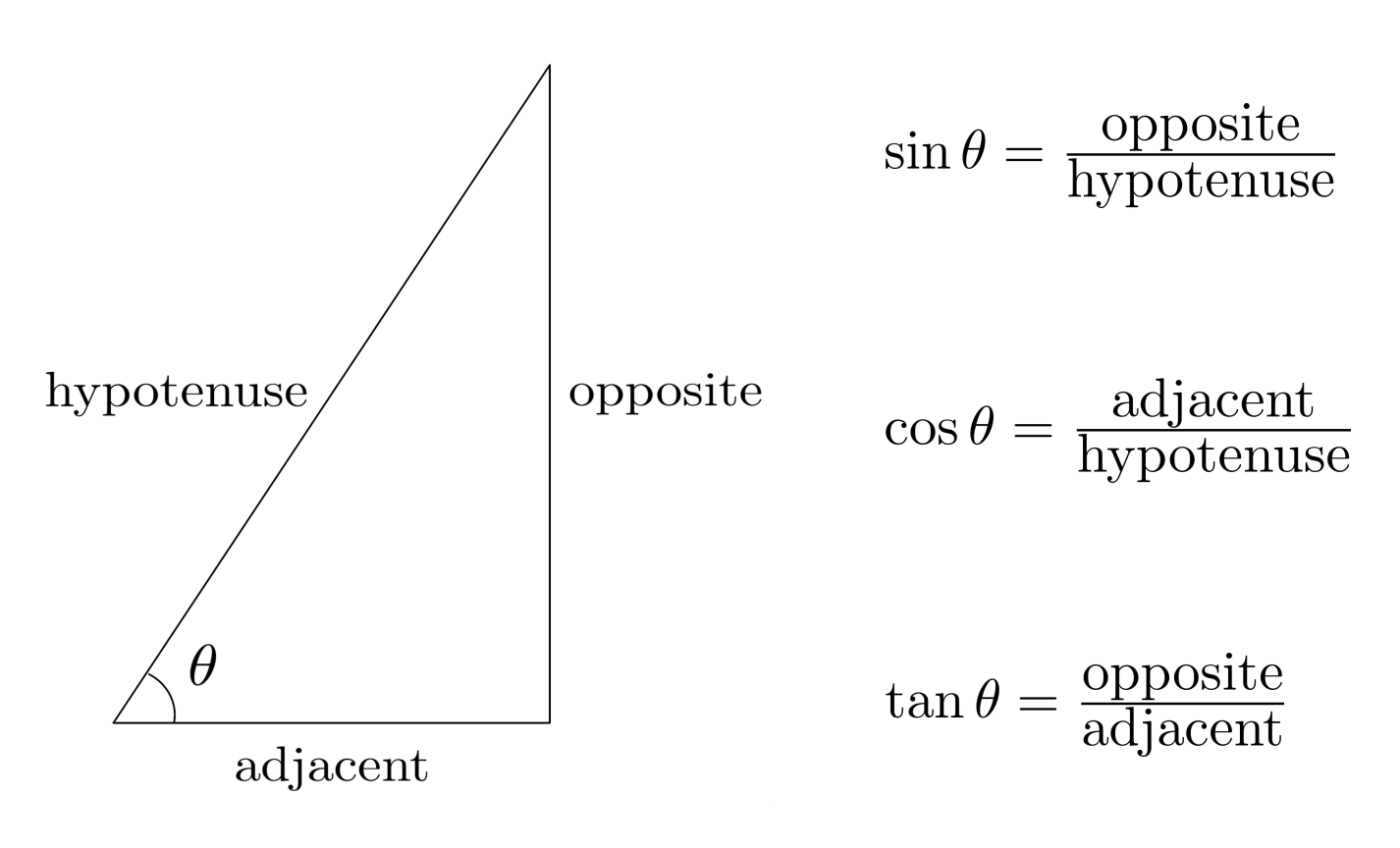
For example, in the triangle below, we have $\sin \theta = \frac{4}{5}$, $\cos \theta = \frac{3}{5}$, and $\tan \theta = \frac{4}{3}$.

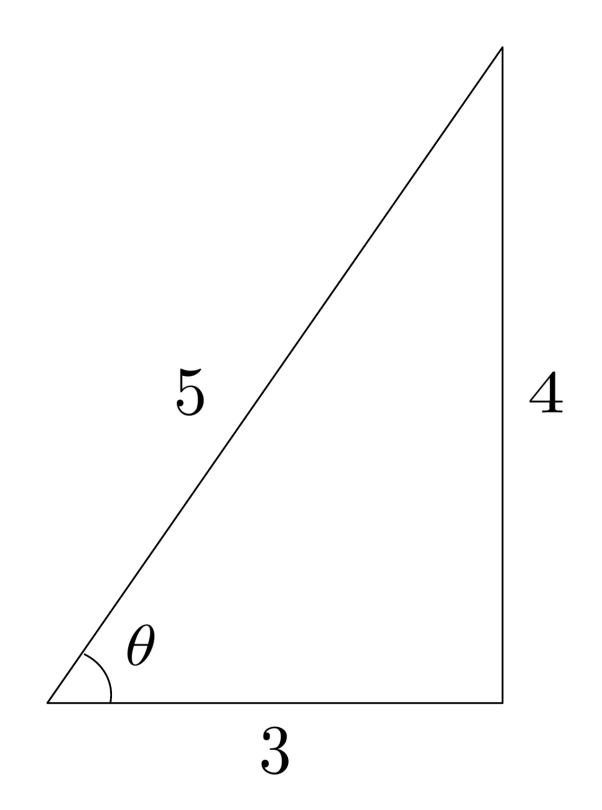
Solving for a Side

Trig functions can be used to solve for unknown side lengths in right triangles. For example, if we know that an angle is $25^\circ$, the opposite side has a length of $10$, and we want to find the hypotenuse, we can set up and solve an equation using sine.

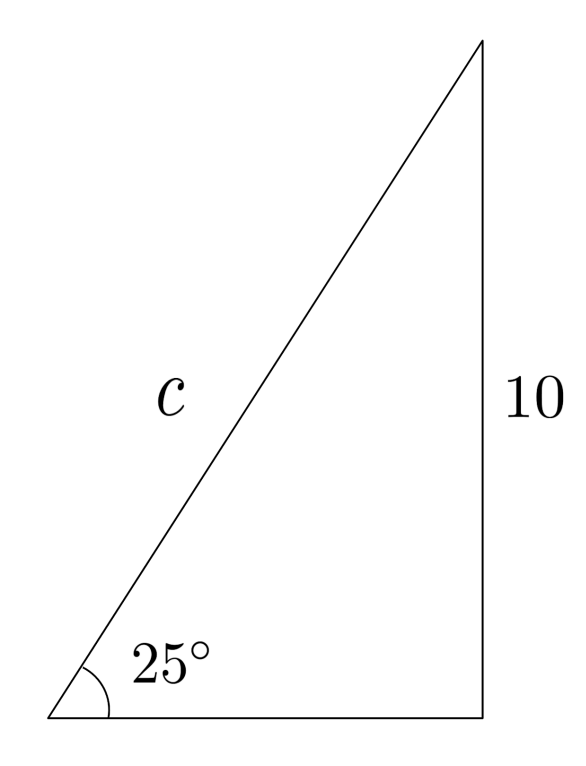
To find the remaining side, we can use any of three methods: Pythagorean theorem, cosine, or tangent.

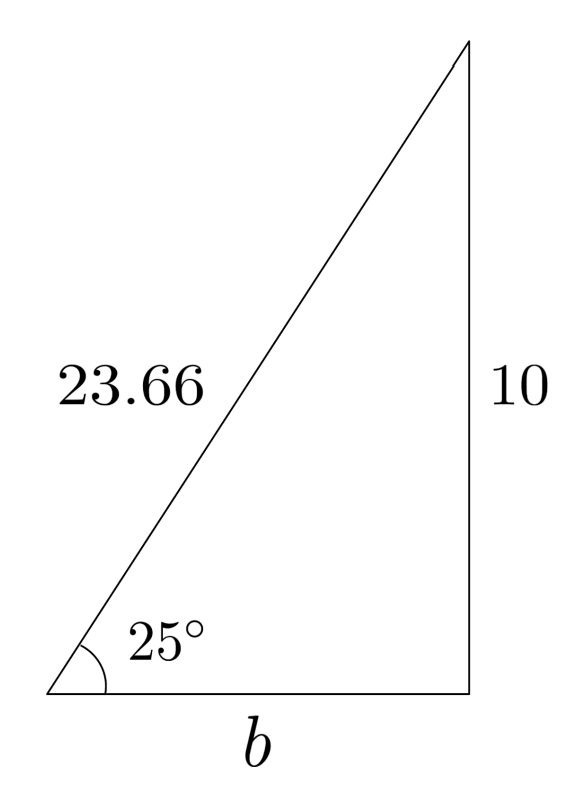
No matter which technique we use, we will end up with the same result (though if we use our approximation of $c \approx 23.66$, we might be slightly off due to rounding error).

Solving for an Angle

Similarly, using inverse trig functions, we can solve for unknown angles in right triangles.

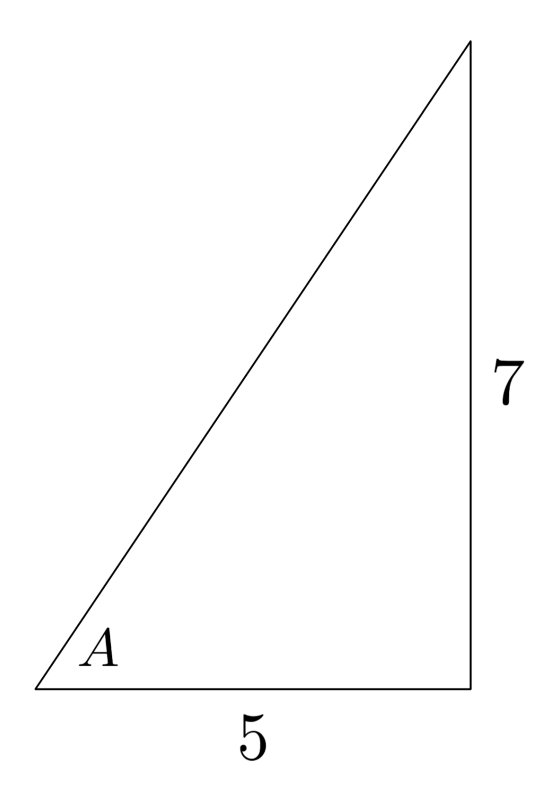
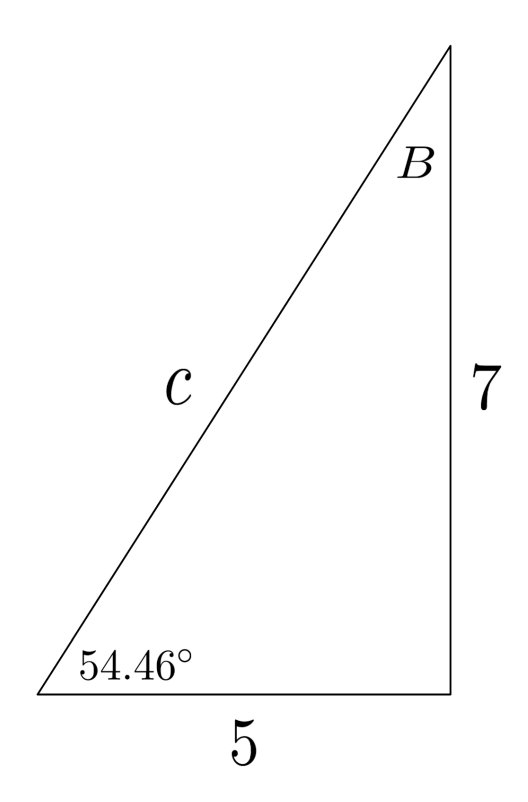
For example, if we know that the adjacent side is $5$ and the opposite side is $7$, we can set up an equation with tangent and then use inverse tangent to find the angle.

The Unit Circle

To find the remaining angle, we can use any of three methods: sum of degrees in a triangle, tangent, or Pythagorean theorem followed by sine or cosine. Regardless of which method we choose, we will end up with the same result.

To gain a better understanding of trig functions, we can imagine putting a triangle inside of a circle on the coordinate plane.

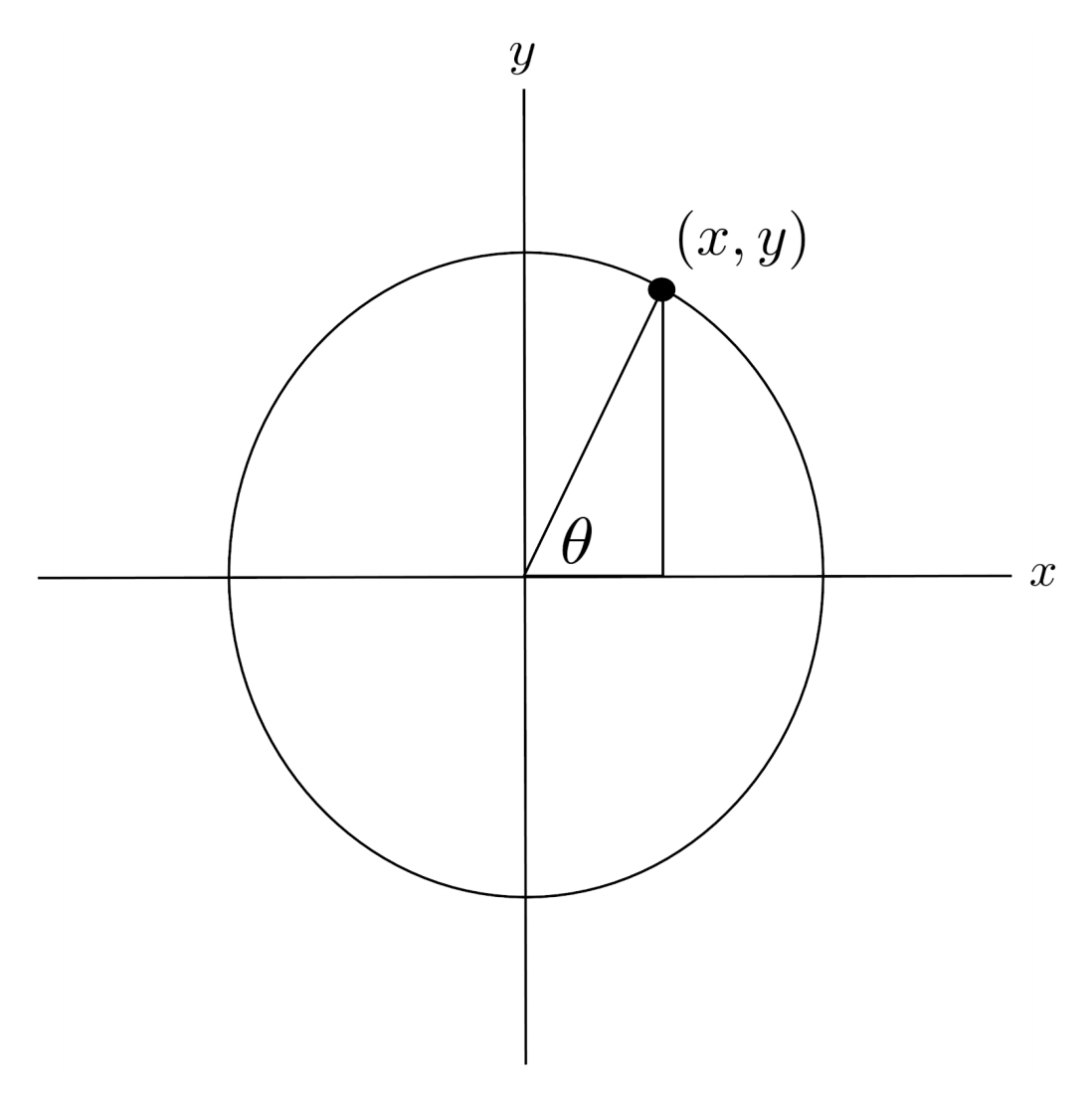
The coordinates of the corner point $(x,y)$ on the circle then tell us the other two sides of the triangle: the horizontal side has length $x$ and the vertical side has length $y$. If we make the circle have radius $1$, then the hypotenuse of the triangle is $1$, and we have

and our point $(x,y)$ can be written as $(\cos \theta, \sin \theta)$.

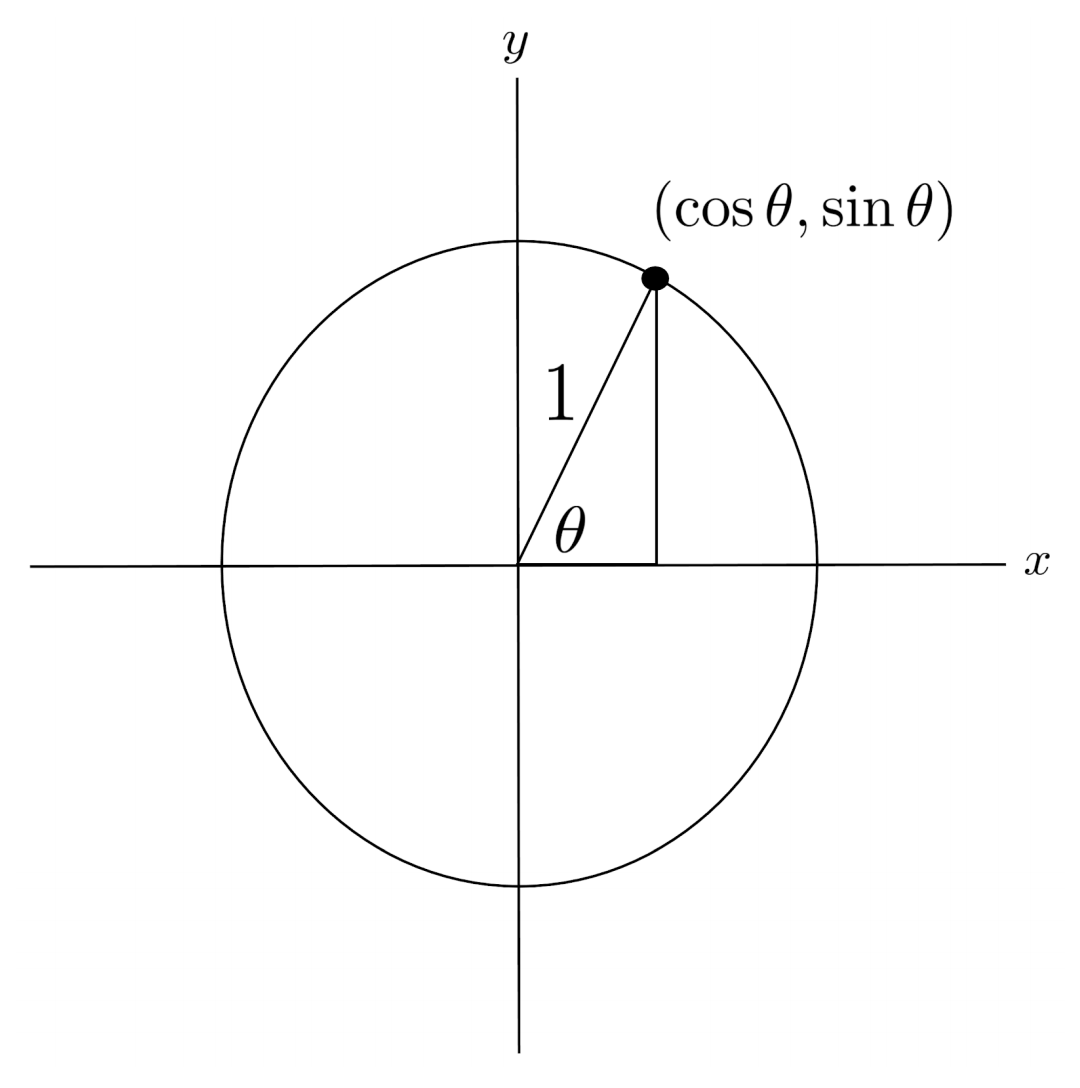
Immediately, we notice two important things. First, using the Pythagorean theorem on the triangle, we see that

This is a handy equation that can be useful in simplifying trigonometric expressions. For example, the expression $(\sin \theta + \cos \theta)^2 + (\sin \theta - \cos \theta)^2$ is actually just equivalent to $2$.

Second, angles repeat every $360^\circ$, since going $360^\circ$ around the circle brings us back to the starting point of $0^\circ$.

That means, for example, that $\sin 390^\circ$ and $\sin -330^\circ$ are both equivalent to $\sin 30^\circ$.

Special Angles

For most angles, a calculator is needed to compute the corresponding trig function values. However, at particular angle measures, the trig functions have simple, exact values:

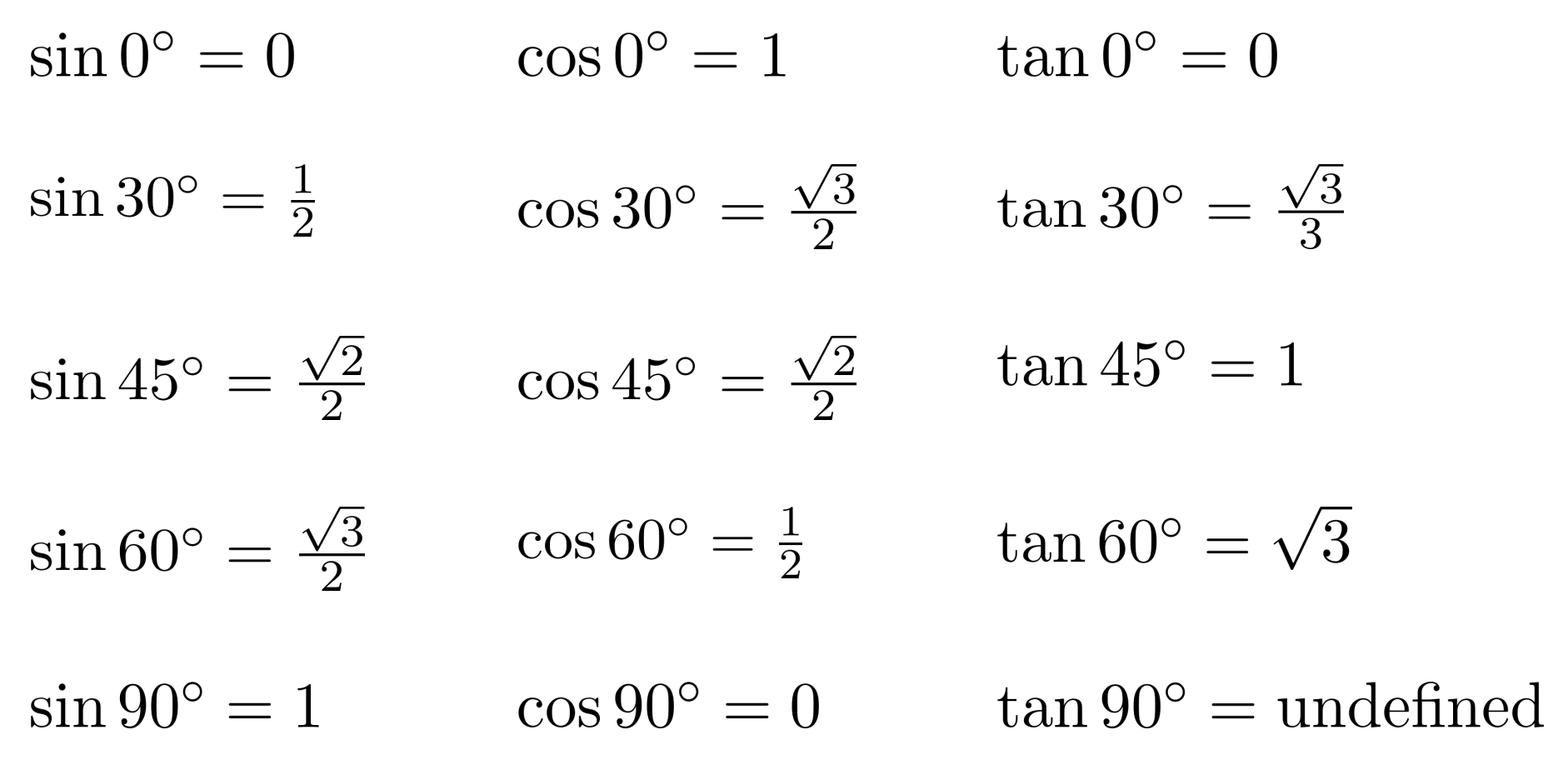
We can remember which values correspond to which angles and which trig functions by thinking about them visually in the unit circle and mentally pairing $\frac{ \sqrt{3}}{2}$ with $\frac{1}{2}$.

• • At $30^\circ$, the x-coordinate is bigger than the y-coordinate, so the x-coordinate must be $\frac{\sqrt{3}}{2}$ and the y-coordinate must be $\frac{1}{2}$.
• • At $60^\circ$, this is reversed. At $45^\circ$, the x-coordinate and y-coordinate are the same, so they both are $\frac{\sqrt{2}}{2}$.
• • At $0^\circ$, we're on the x-axis, so the x-coordinate is $1$ and the y-coordinate is $0$.
• • At $90^\circ$, we're on the y-axis, so the y-coordinate is $1$ and the x-coordinate is $0$.

To get tangent, we can just take the ratio of the y-coordinate to the x-coordinate.

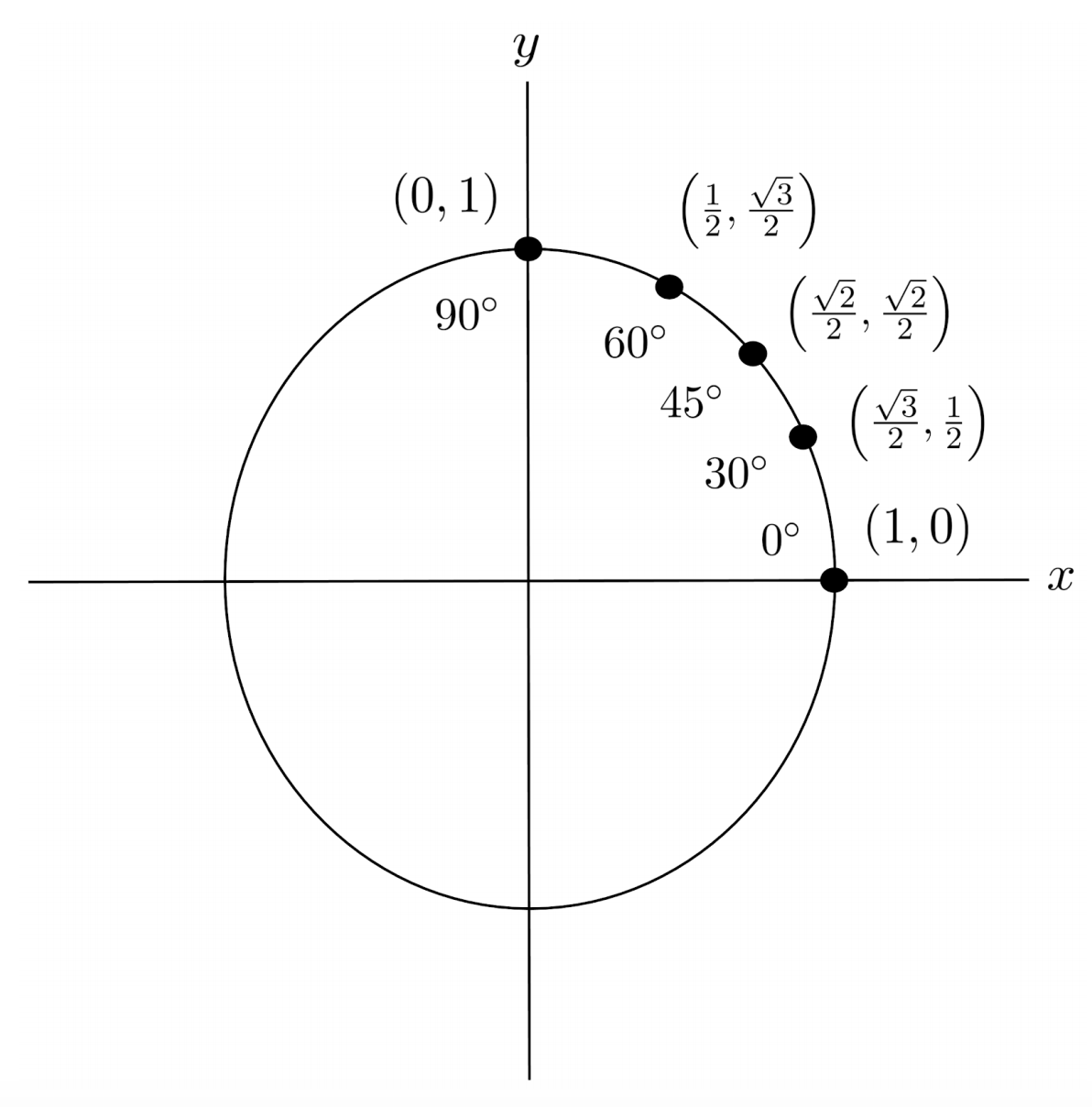
Using symmetry, we can label angles in the other three quadrants of the circle.

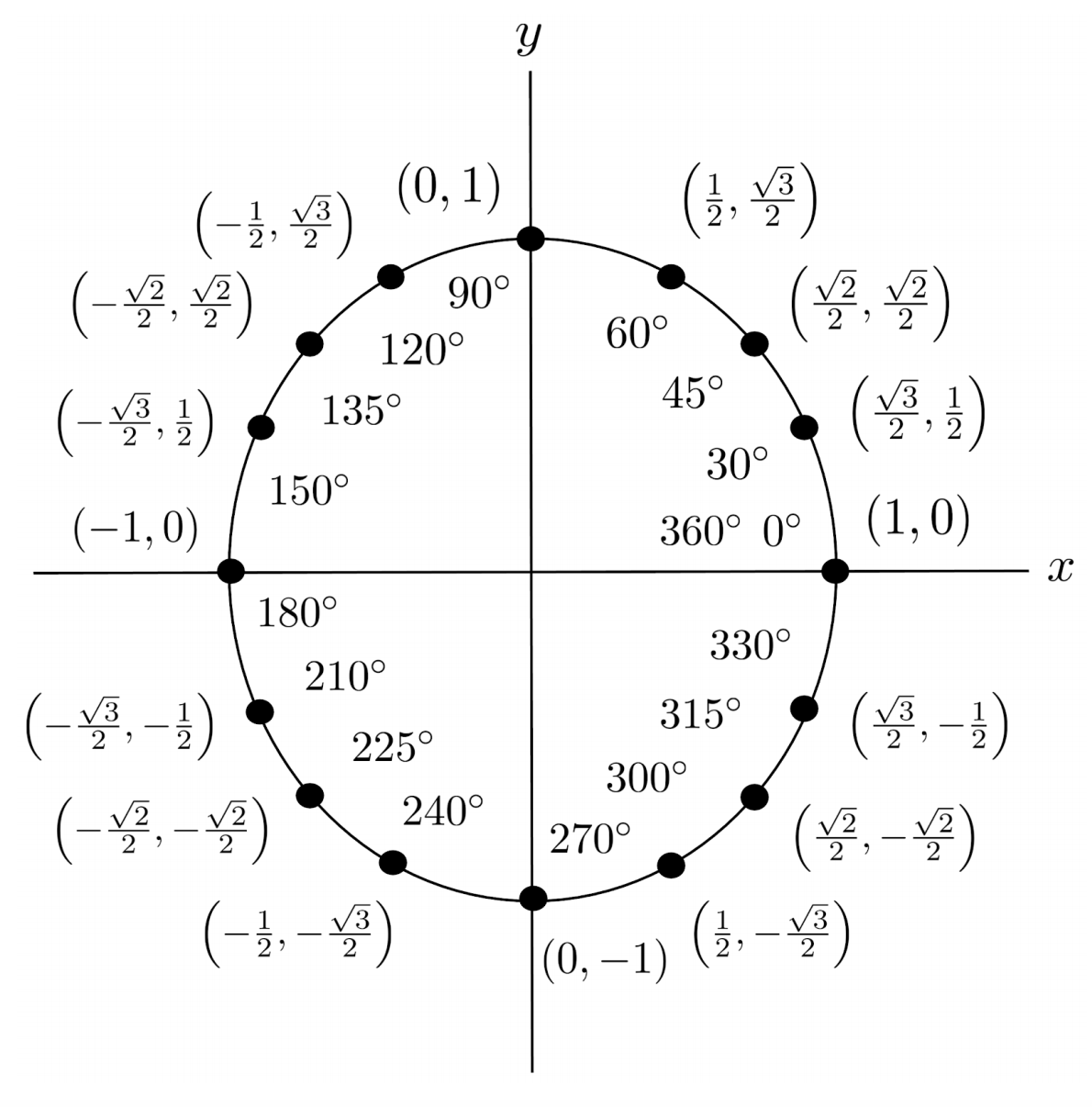
Derivation of Special Angles

You might be wondering where the values $\frac{1}{2}$, $\frac{\sqrt{2}}{2}$, and $\frac{\sqrt{3}}{2}$ come from in the first place.

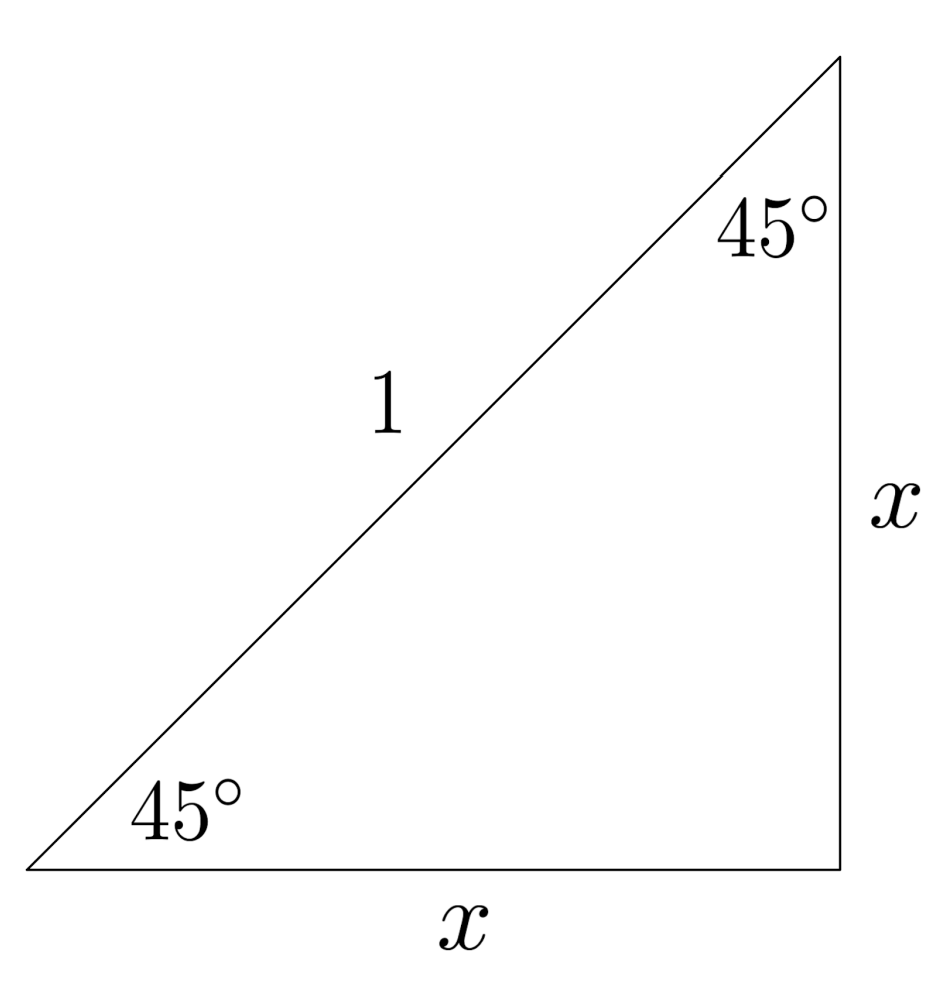
To see where $\frac{\sqrt{2}}{2}$ comes from, we can construct a right triangle with a hypotenuse of $1$ and an angle of $45^\circ$.

The other angle must also be $45^\circ$, so the triangle’s two legs must be equal in length, and we can use the Pythagorean theorem to discover that the length of each leg is $\frac{ \sqrt{2}}{2}$.

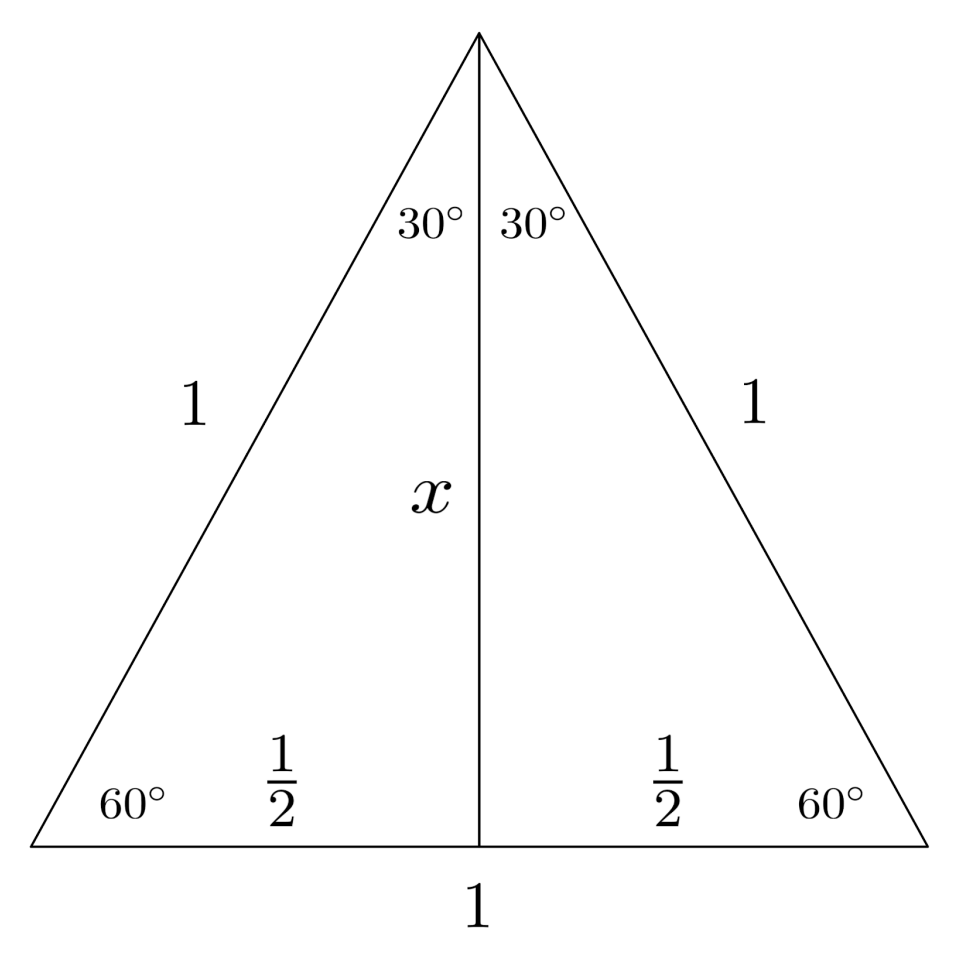
Likewise, to see where $\frac{1}{2}$ and $\frac{\sqrt{3}}{2}$ come from, we can construct a right triangle with a hypotenuse of $1$ and an angle of $60^\circ$.

The other angle must be $30^\circ$, which is exactly half – consequently, we can combine two of these triangles to form an equilateral triangle whose side lengths are all equal to the hypotenuse of $1$.

The shortest sides of the two triangles together make up a side of the equilateral triangle, which we know has length $1$, so the shortest sides of the two triangles must each be $\frac{1}{2}$. Using the Pythagorean theorem, we find that the length of the other leg is $\frac{\sqrt{3}}{2}$.

Graphs

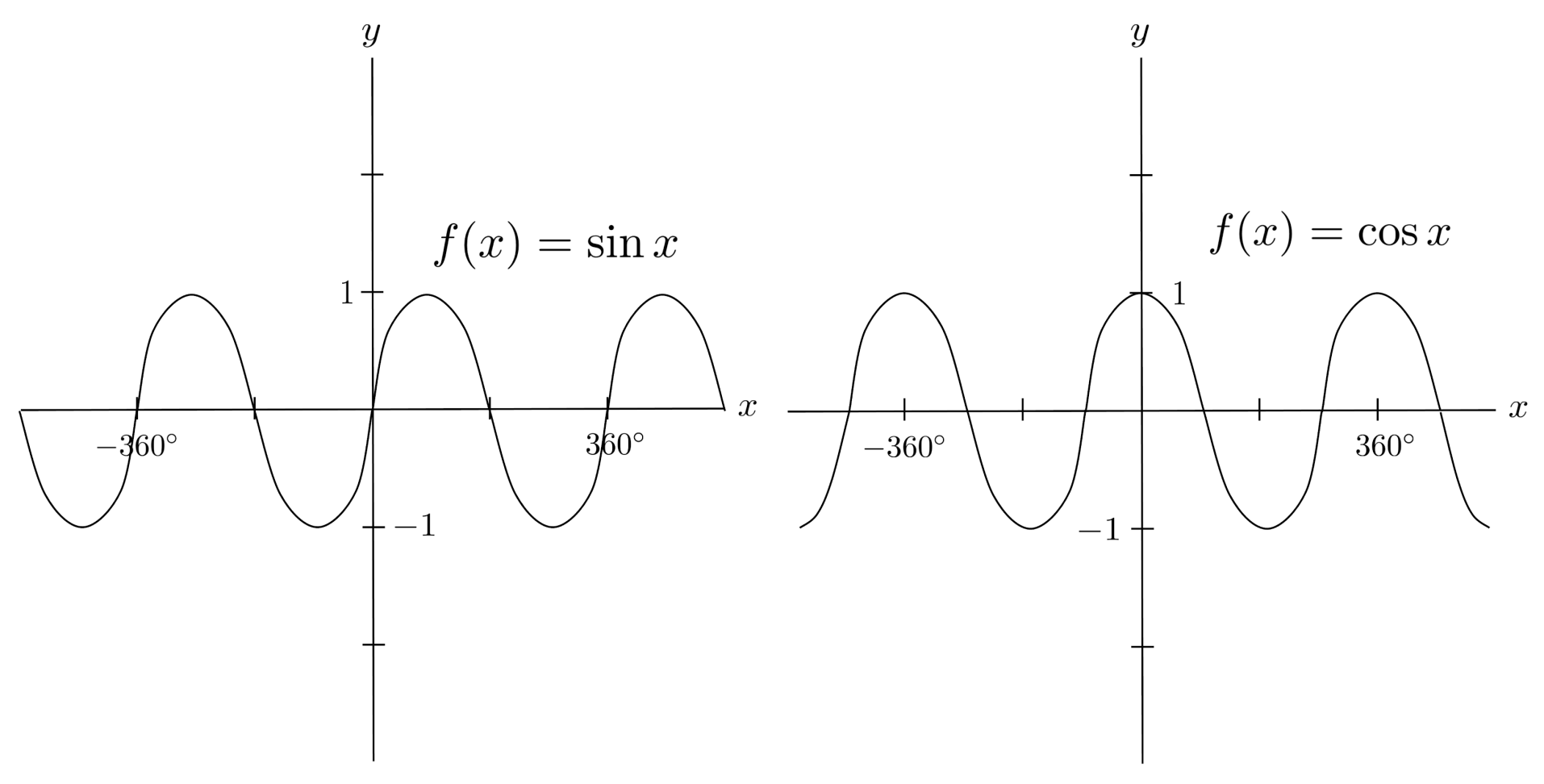
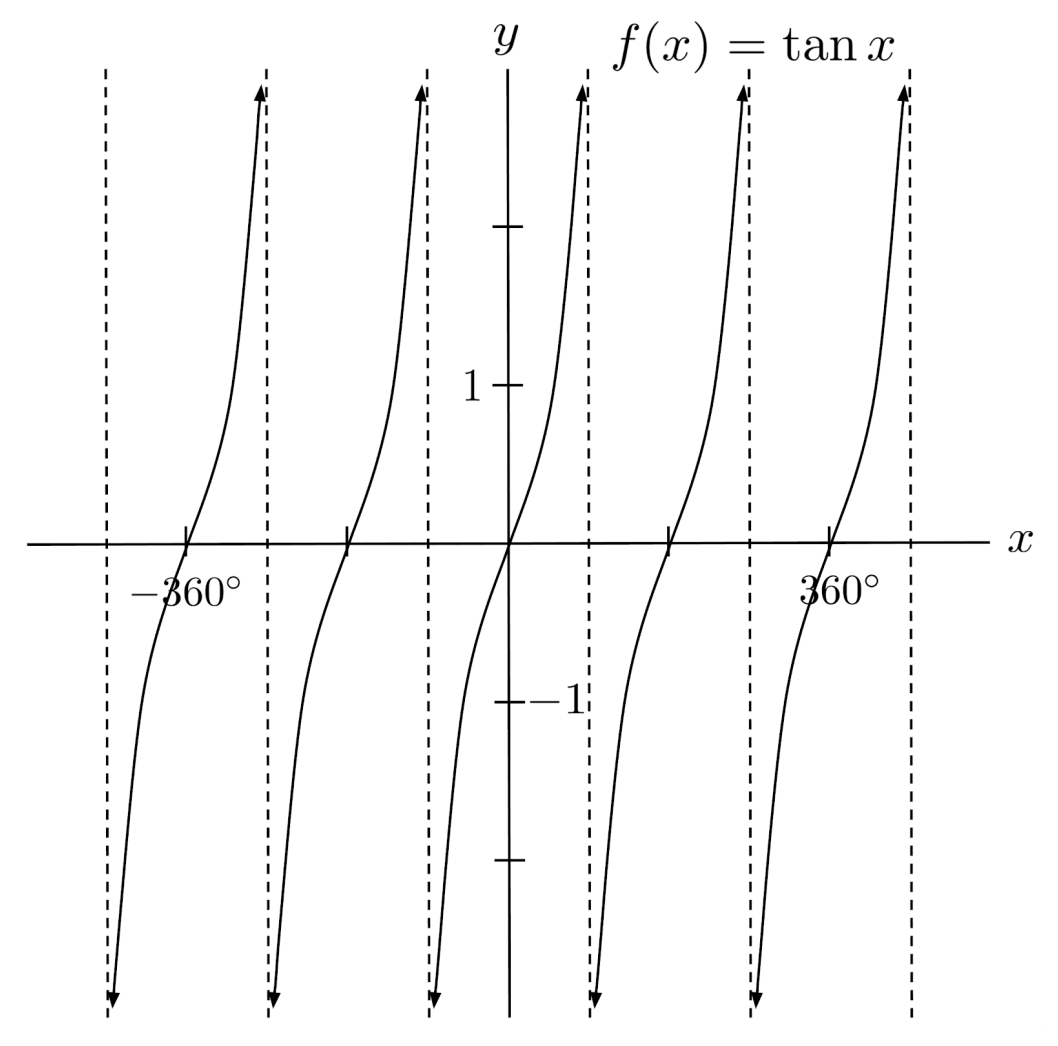
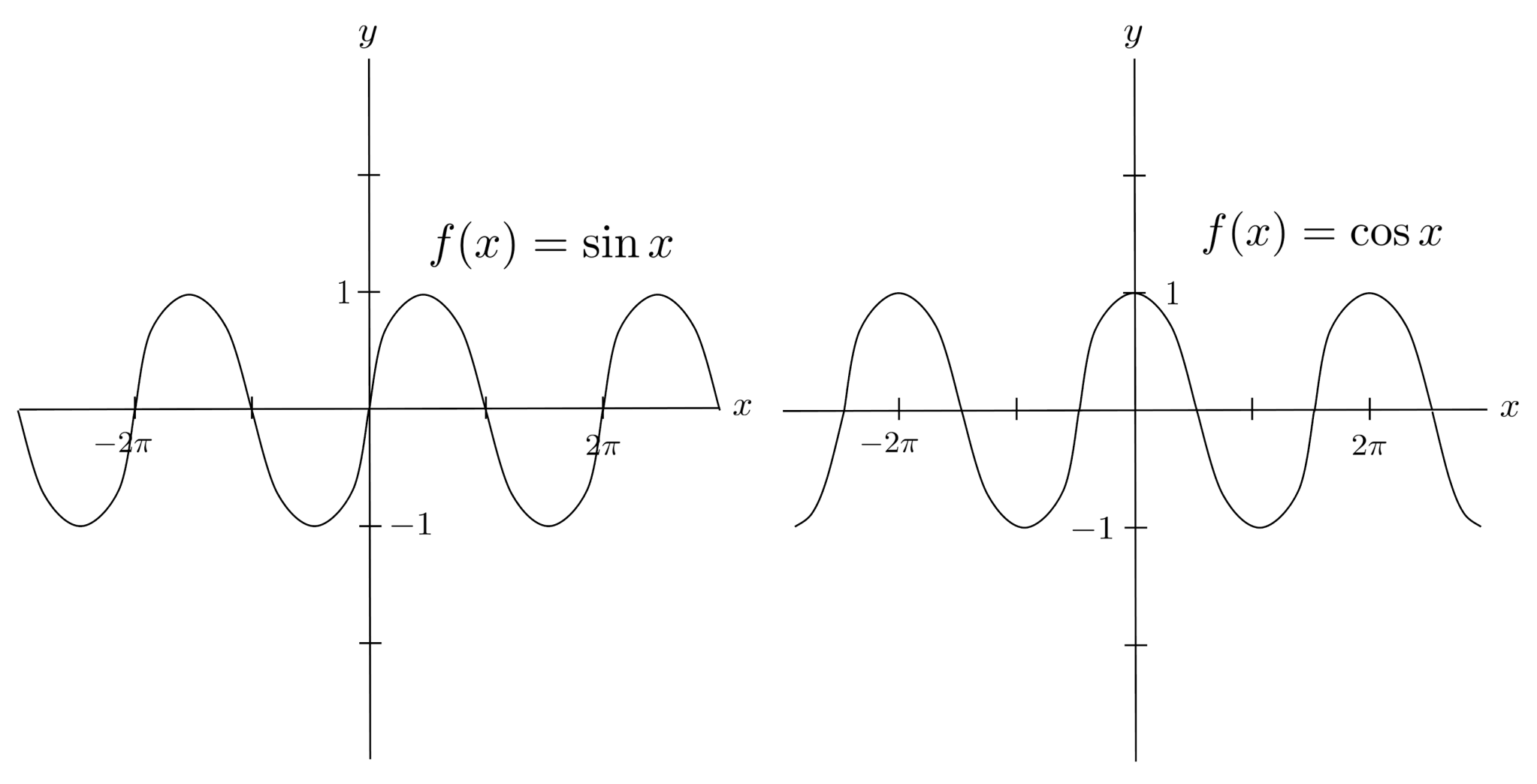
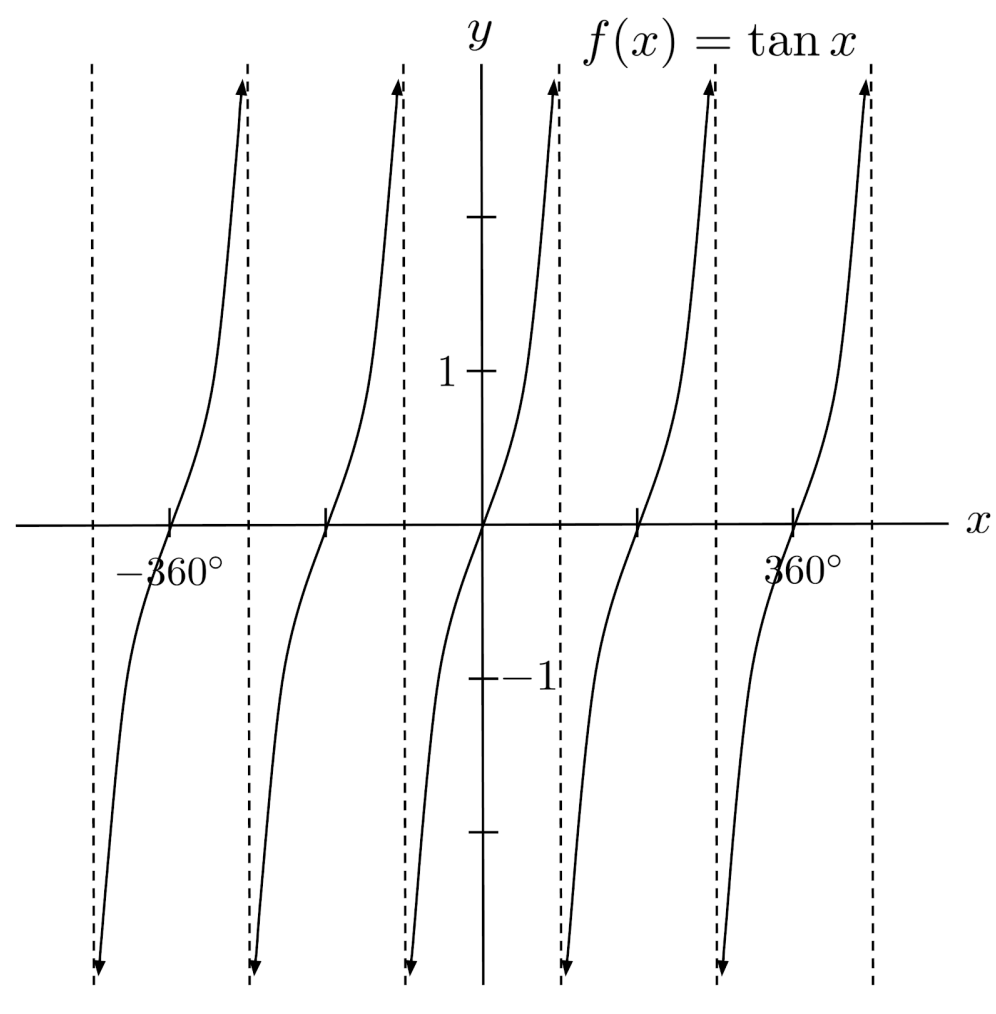
The graphs of sine, cosine, and tangent are drawn below. They repeat every $360^\circ$, since $360^\circ$ is one full revolution around the unit circle and thus brings us full-circle back to the starting point.

Tangent actually repeats twice every $360^\circ$ (or once every $180^\circ$) because it goes from positive to negative from the first to second quadrant, and again positive to negative from the third to fourth quadrant.

To make sense of the shapes of the graphs, try to trace out the trig function values while following around the unit circle.

Radians

The standard way to measure angles is actually not in degrees – rather, it is in radians. One radian is equivalent to the angle whose arc is equal to one radius of a circle.

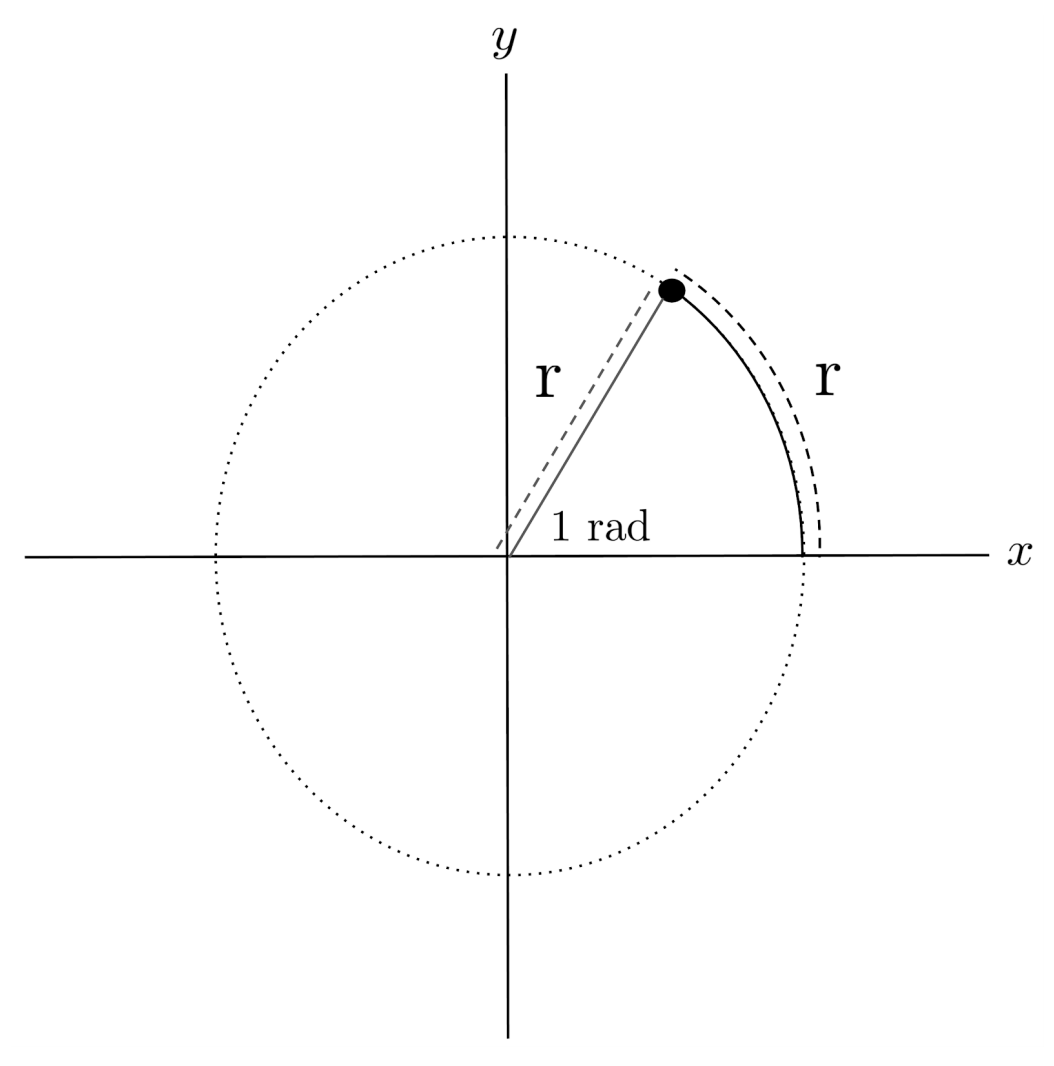
Since the full arc length (circumference) of the circle is $2\pi$ times the radius, a full $360^\circ$ around the circle is equivalent to $2\pi$ radians.

Below is a copy of the unit circle, using radians instead of degrees.

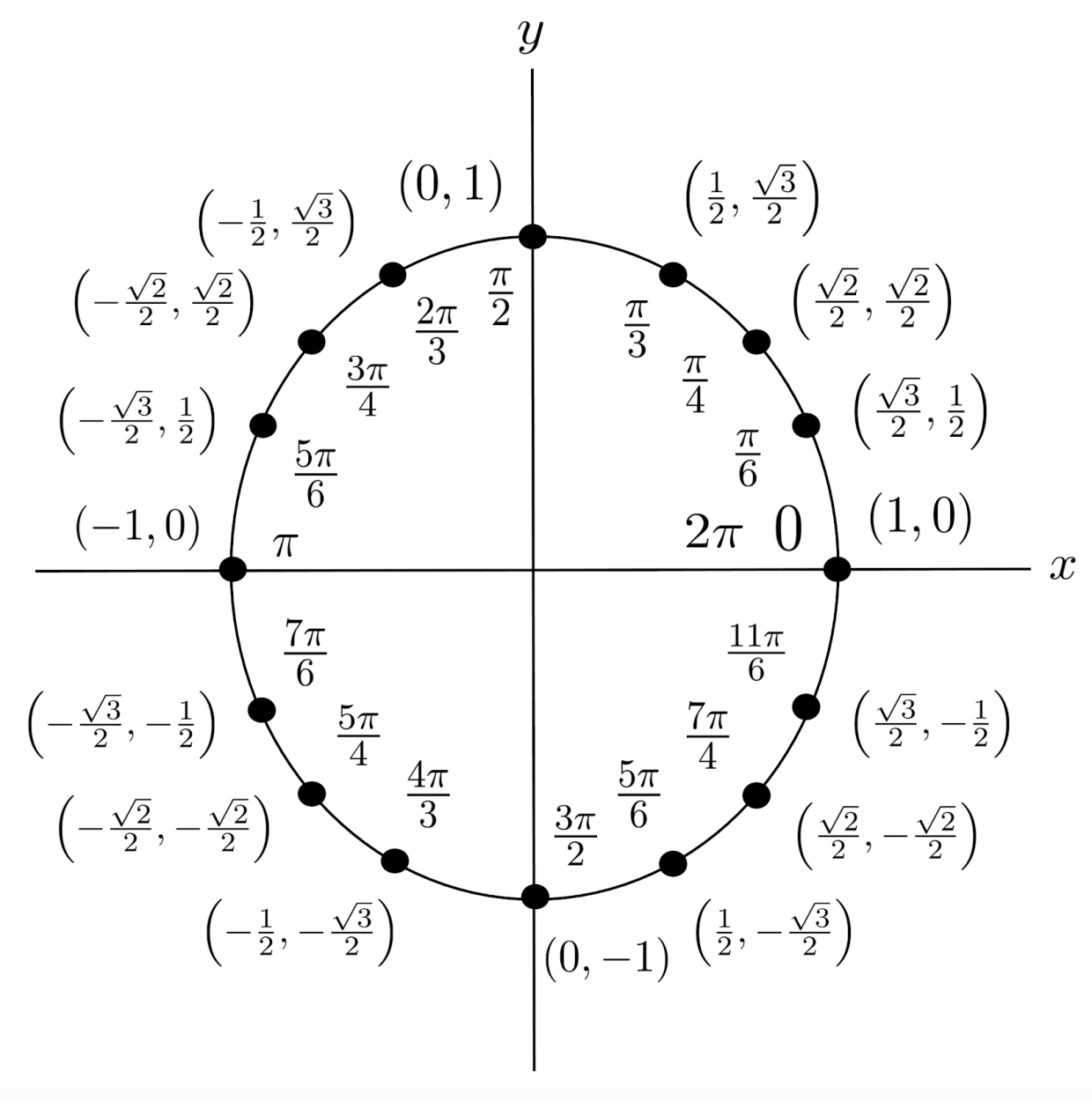
The trig functions are graphed in terms of radians below. Nothing changes, except for the units of the x-axis.

Reciprocal Trigonometric Functions

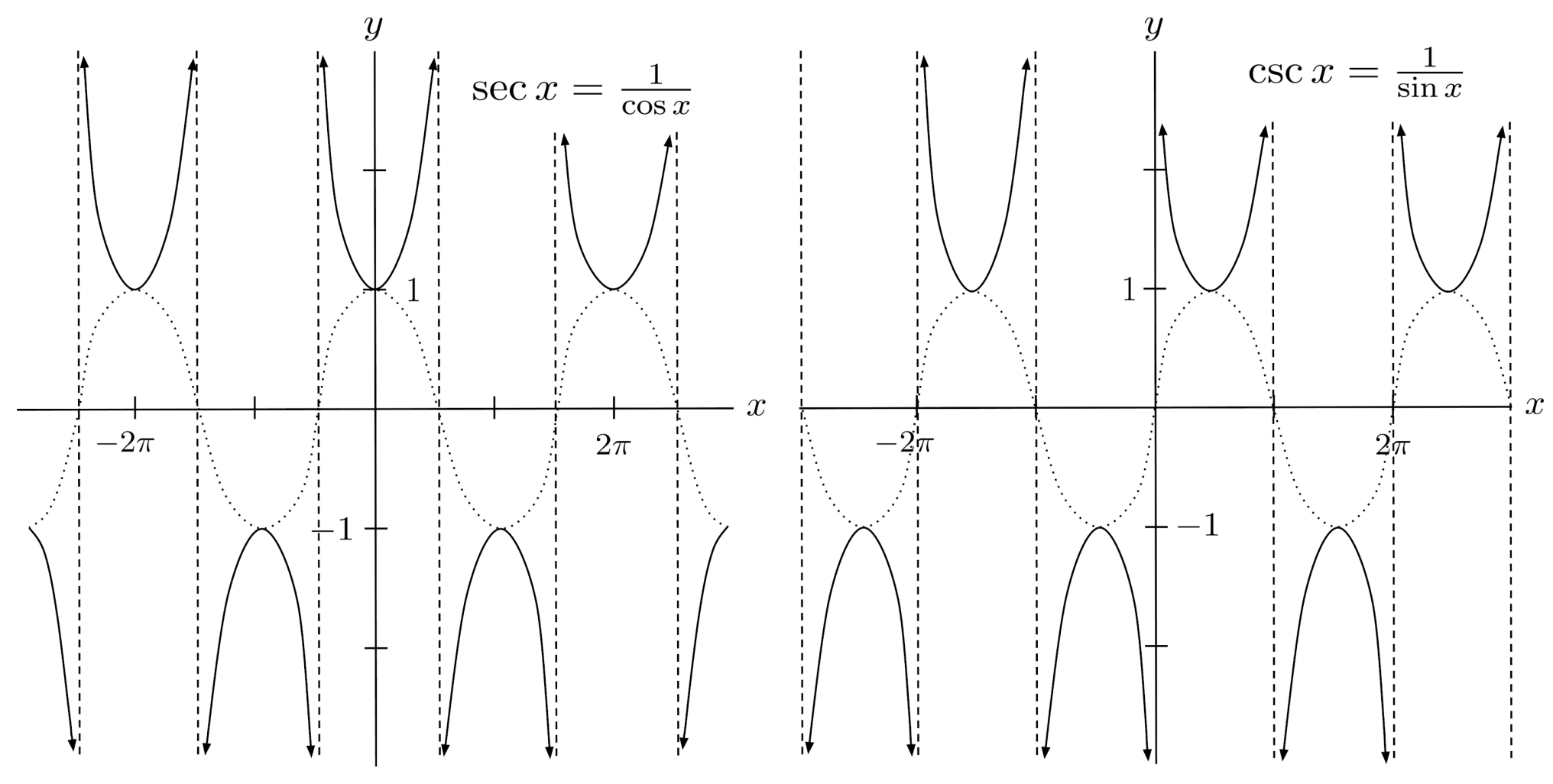
There are three other trig functions: secant, cosecant, and cotangent. They are just the reciprocals of cosine, sine, and tangent.

Consequently, they can be understood by thinking about the properties of cosine, sine, and tangent. We will not explore them further, but we include their graphs below.

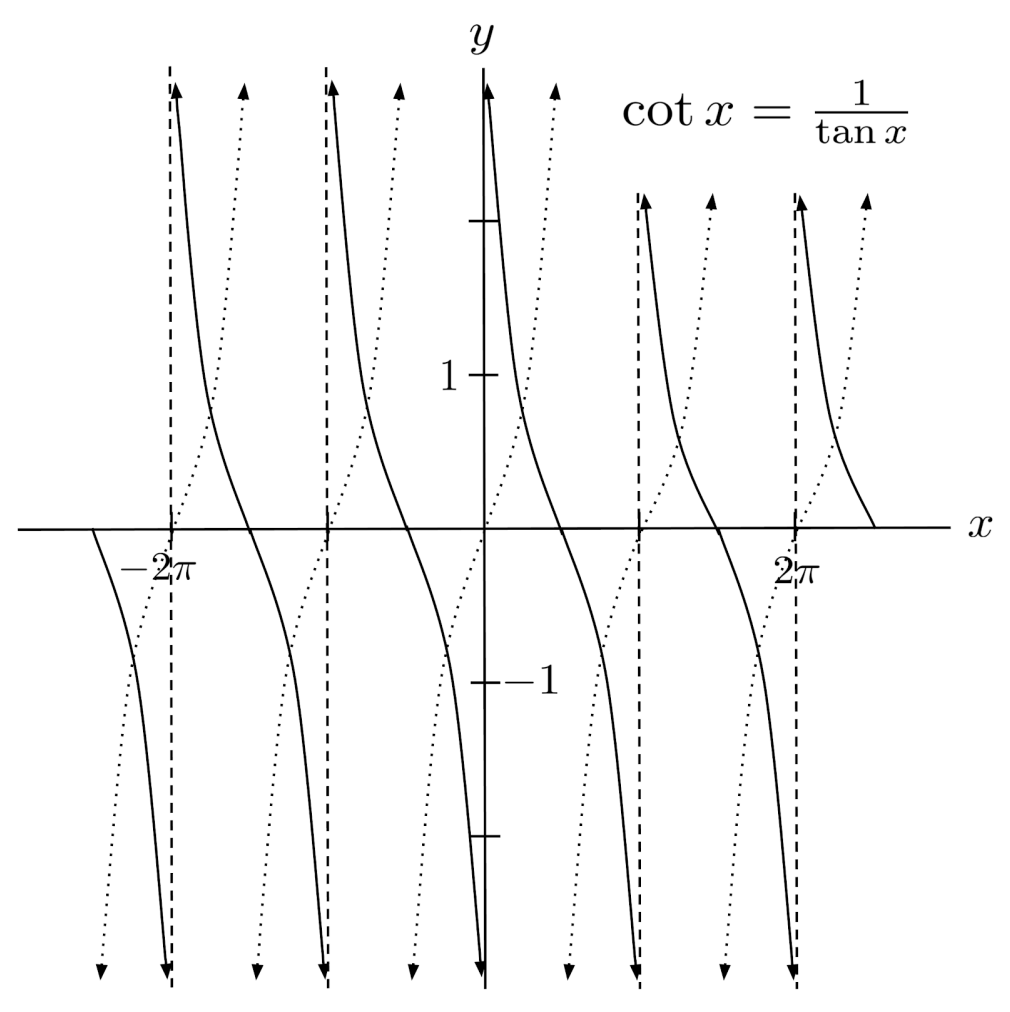
Exercises

Use trigonometry to find the missing sides and angles of the triangles. (You can view the solution by clicking on the problem.)

$1)$

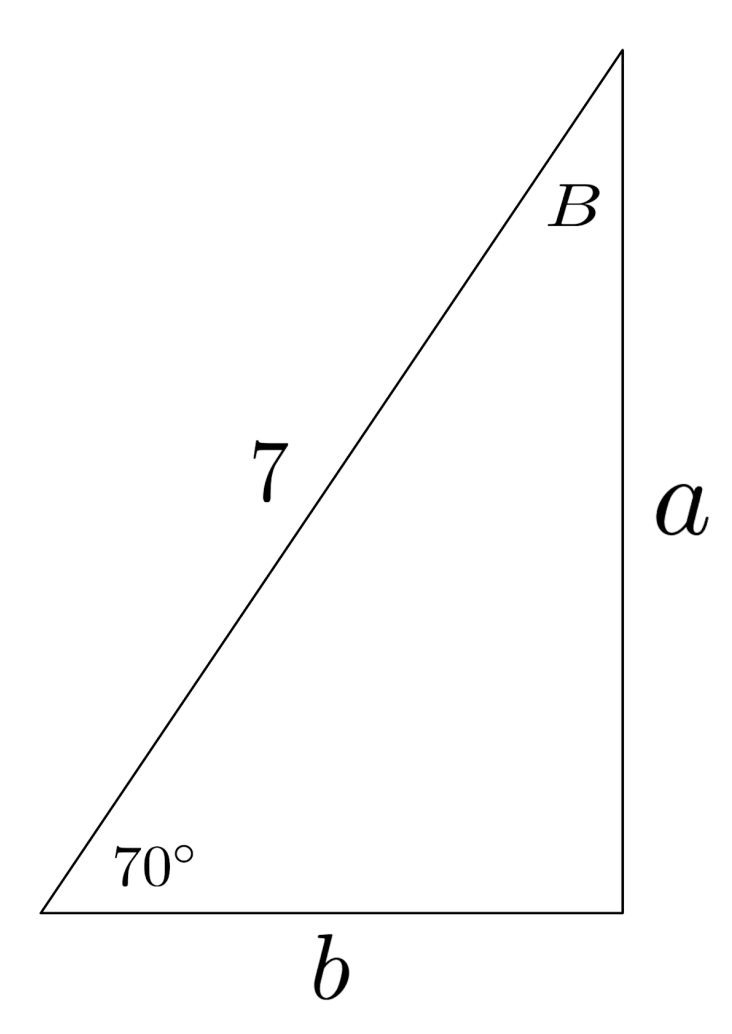
Solution:
$a \approx 6.58$
$b \approx 2.39$
$B = 20^\circ$

$2)$

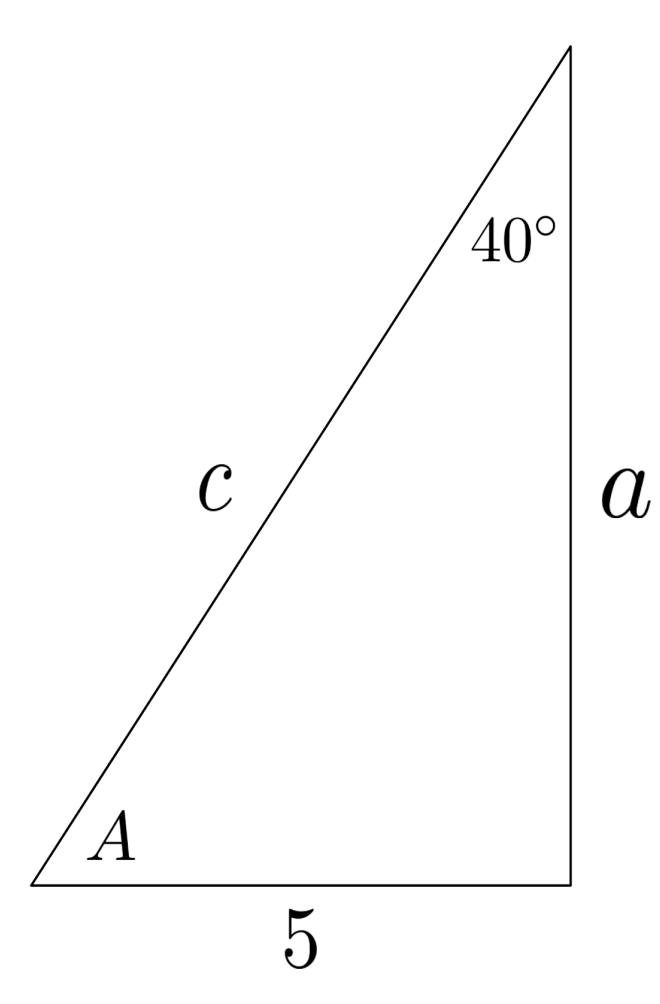
Solution:
$a \approx 5.96$
$c \approx 7.78$
$A = 50^\circ$

$3)$

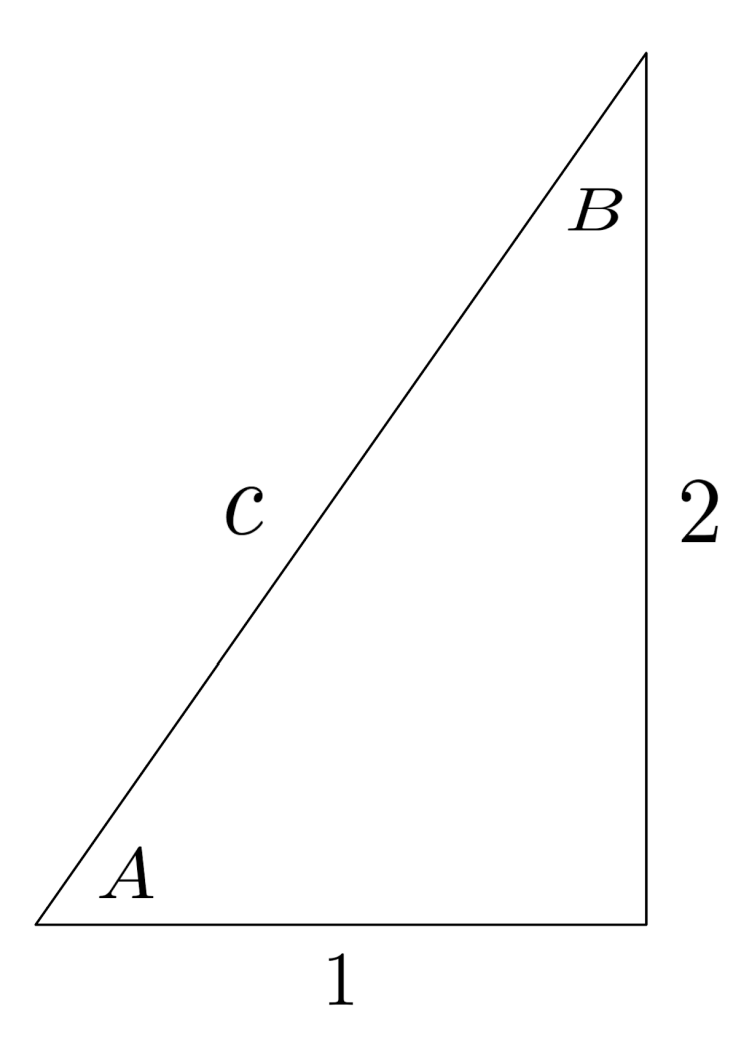
Solution:
$c = \sqrt{5} \approx 2.24$
$A \approx 63.43^\circ$
$B \approx 26.57^\circ$

$4)$

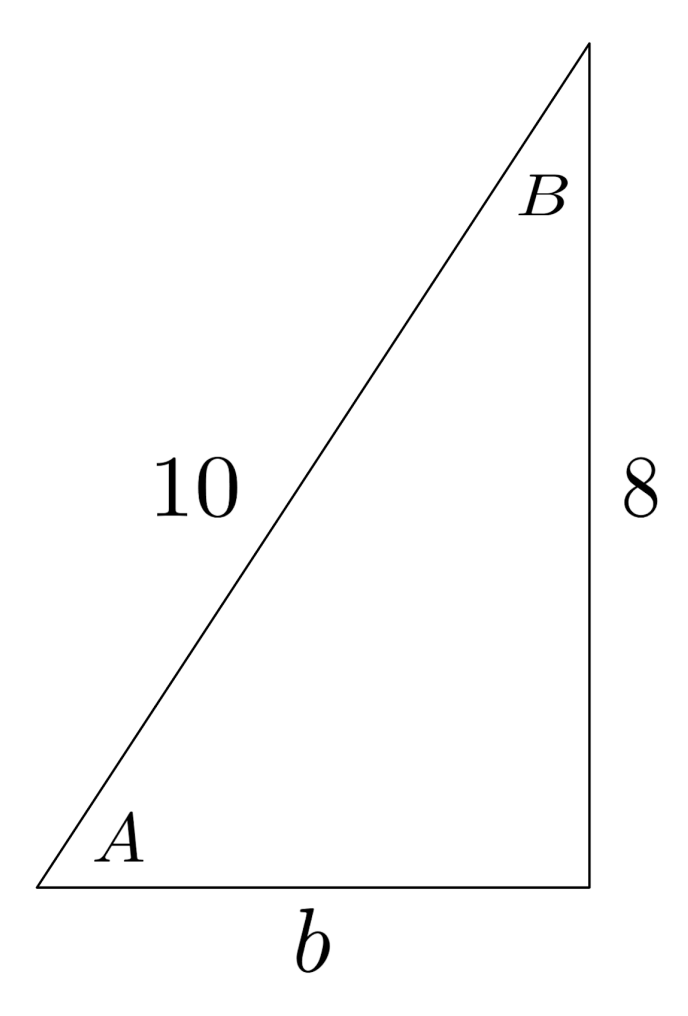
Solution:
$b = 6$
$A \approx 53.13^\circ$
$B \approx 36.87^\circ$

Use the unit circle to find the exact values of the following trigonometric expressions.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Trigonometric Functions. In Justin Math: Algebra. https://justinmath.com/trigonometric-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.