Standard Form of a Quadratic Equation

Quadratic equations are similar to linear equations, except that they contain squares of a single variable.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Standard Form of a Quadratic Equation. In Justin Math: Algebra. https://justinmath.com/standard-form-of-a-quadratic-equation/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Quadratic equations are similar to linear equations, except that they contain squares of a single variable.

For example, the equations below are quadratic equations:

On the other hand, the equations below are not quadratic equations. (A quadratic equation must contain the square of one variable, but cannot contain squares of multiple different variables, and cannot contain other operations not found in linear equations, such as square roots.)

Graphing

As a consequence of the squared variable, the shape of the graph of a two-variable quadratic equation is a parabola.

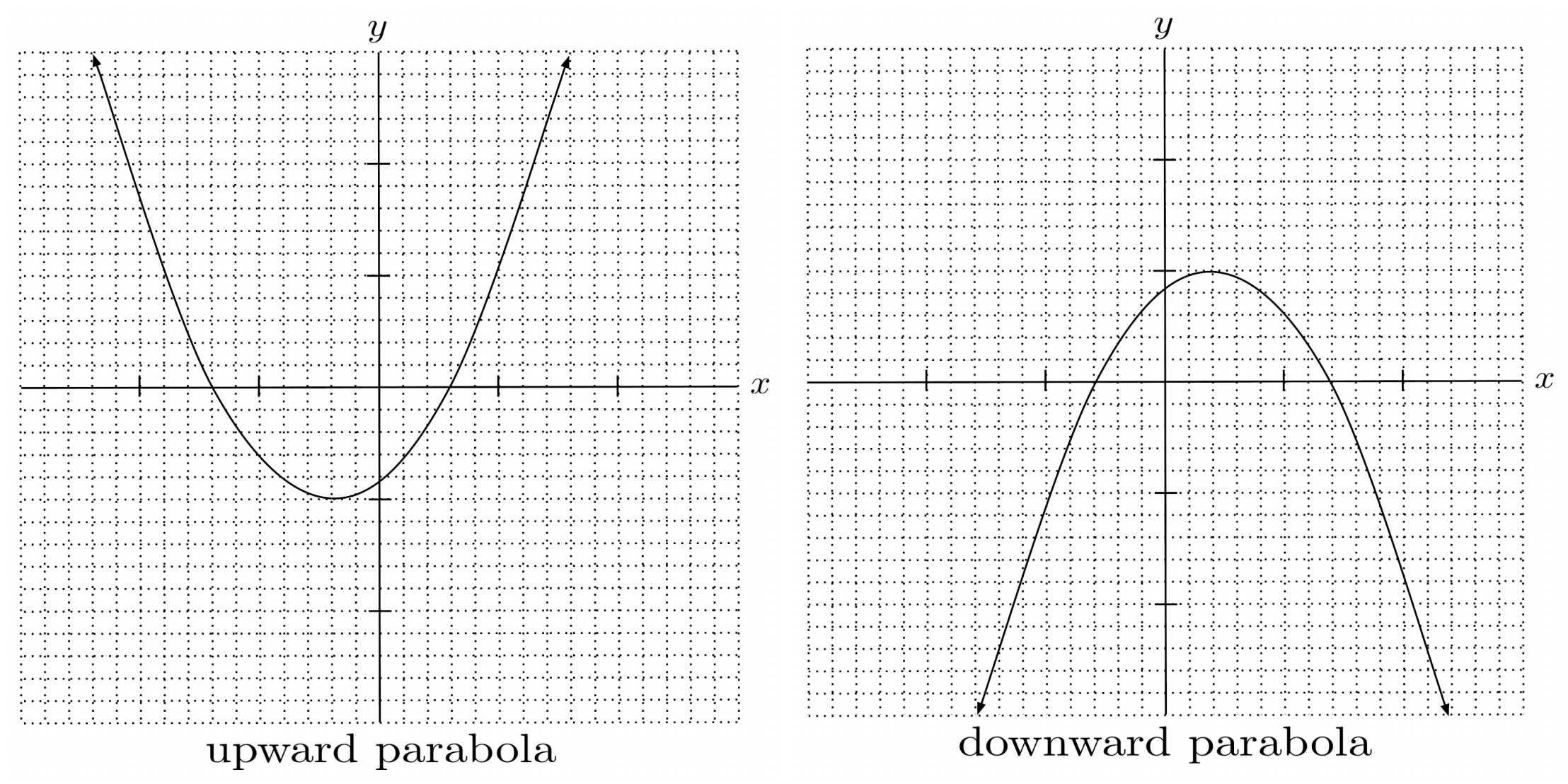
To tell whether the graph of a quadratic equation is an upward or downward parabola, it is helpful to arrange the quadratic equation into standard form, which is given by

where $a$, $b$, and $c$ are constants and called coefficients. The coefficient on the $x^2$ term, which is given by $a$, is often called the leading coefficient because it is the leftmost coefficient when terms in the standard equation are ordered properly.

Keep in mind that some coefficients may be zero – for example, the quadratic equation $y=3x^2+1$ has $b=0$ because it can be written as $y=3x^2+0x+1$.

If the leading coefficient, $a$, is positive, then the parabola opens upward. Otherwise, if the leading coefficient is negative, then the parabola opens downward.

To remember this, you might think of a positive leading coefficient causing the parabola to smile, and a negative leading coefficient causing the parabola to frown.

Sometimes, we may have to rearrange a quadratic equation into standard form.

Vertex of a Parabola

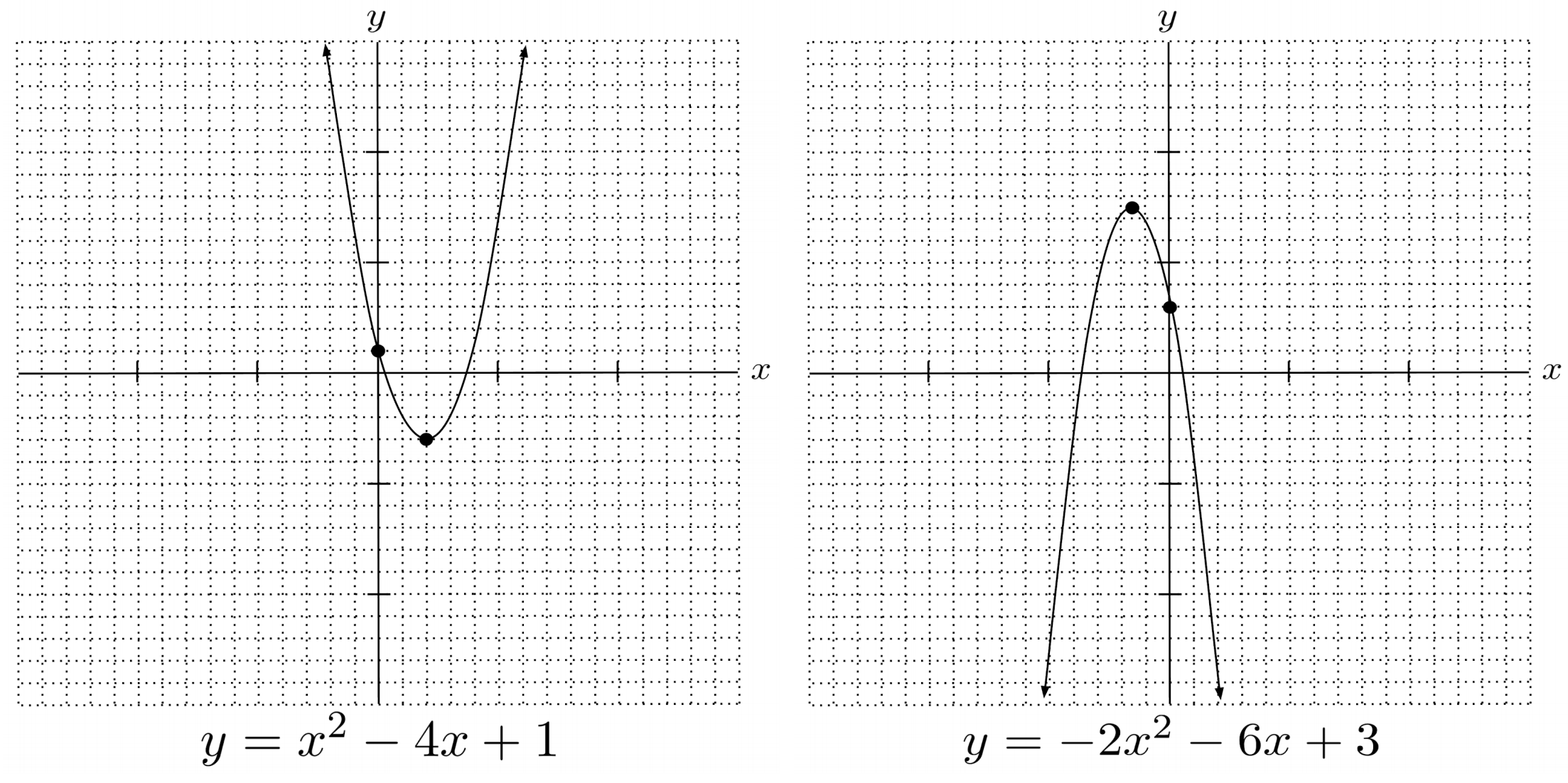
The standard form of a quadratic equation can also tell us about the parabola’s vertex, or turning point.

For a quadratic equation in the form $y=ax^2+bx+c$, the x-coordinate of the vertex is given by $-\frac{b}{2a}$.

To find the y-coordinate of the vertex, we can substitute the x-coordinate of the vertex into the quadratic equation and evaluate.

With a parabola’s vertex and direction of opening, we can draw a decent sketch of the graph.

To make our graph a little more accurate, we can also make sure it has the correct y-intercept. Since we set $x=0$ to find the y-intercept, the y-intercept of $y=ax^2+bx+c$ is always given by $a(0)^2+b(0)+c$, which evaluates simply to $c$.

Exercises

For the following quadratic equations:

1. Write the quadratic equation in standard form.
2. Using the standard form, tell whether the parabola opens upward or downward, and find the vertex and y-intercept.
3. Finally, using the parabola's vertex, opening direction, and y-intercept, draw a rough sketch of the graph of the equation. (If the vertex and the y-intercept are the same, choose some other point.)

(You can view the solution by clicking on the problem.)

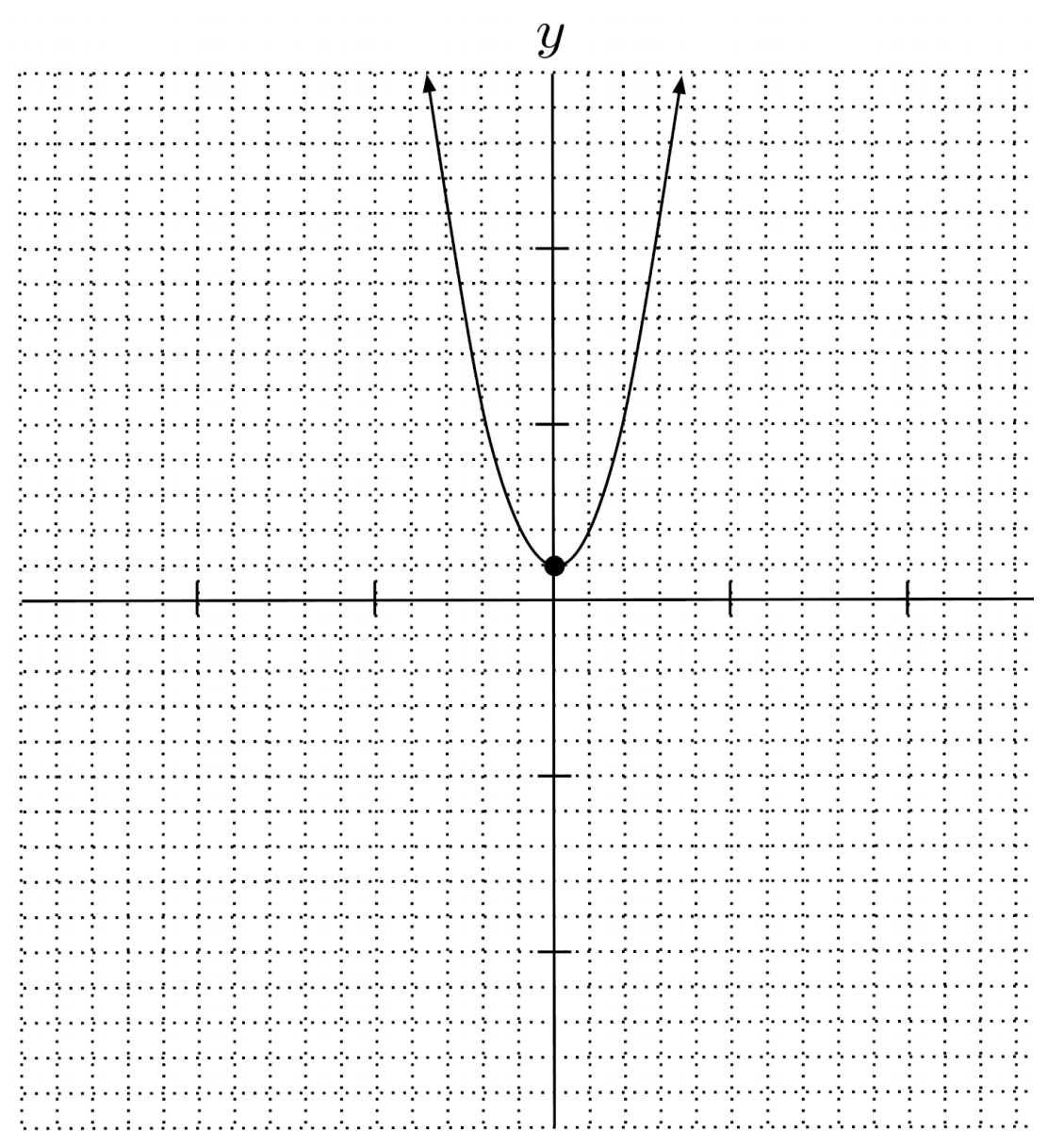
$1) \hspace{.5cm} y=1+x^2$

Solution:
$y=x^2+1$
$\text{up} \hspace{.5cm} (0,1) \hspace{.5cm} 1$

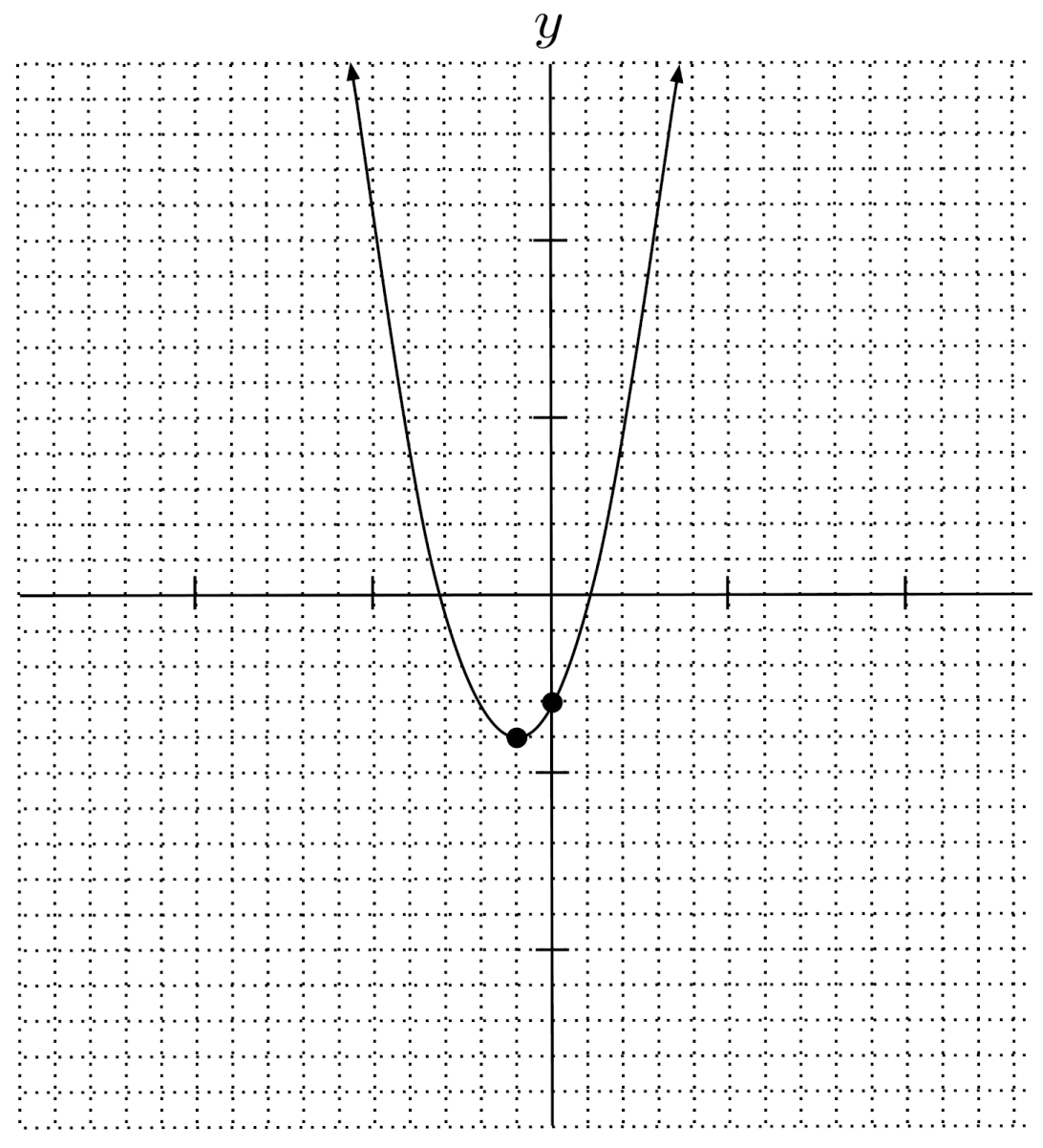
$2) \hspace{.5cm} y=2x+x^2-3$

Solution:
$y=x^2+2x-3$
$\text{up} \hspace{.5cm} (-1,-4) \hspace{.5cm} -3$

$3) \hspace{.5cm} y=2(2x-1)-x^2$

Solution:
$y=-x^2+4x-2$
$\text{down} \hspace{.5cm} (2,2) \hspace{.5cm} -2$

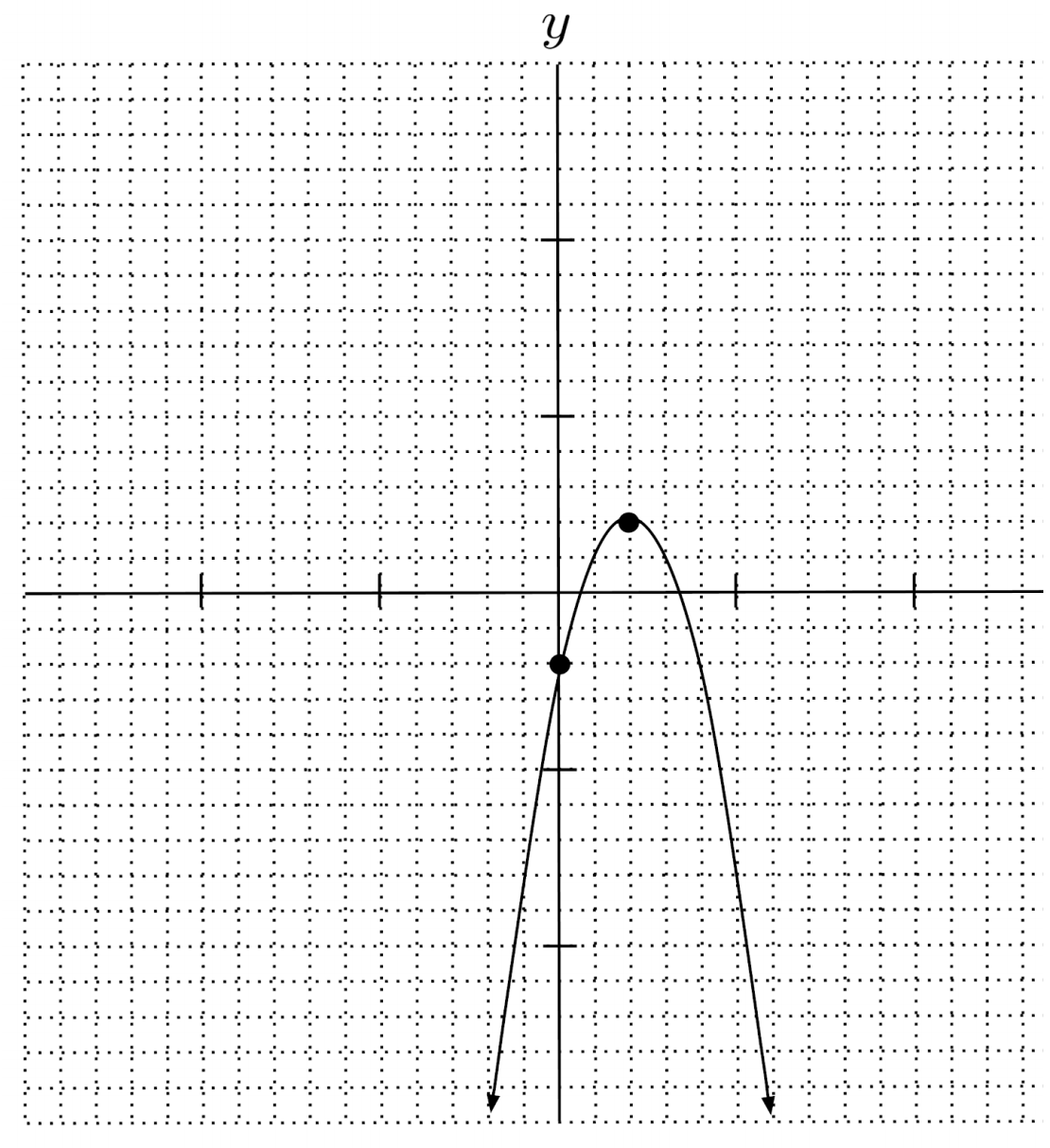
$4) \hspace{.5cm} y=2x(x+4)$

Solution:
$y=2x^2+8x$
$\text{up} \hspace{.5cm} (-2,-8) \hspace{.5cm} 0$

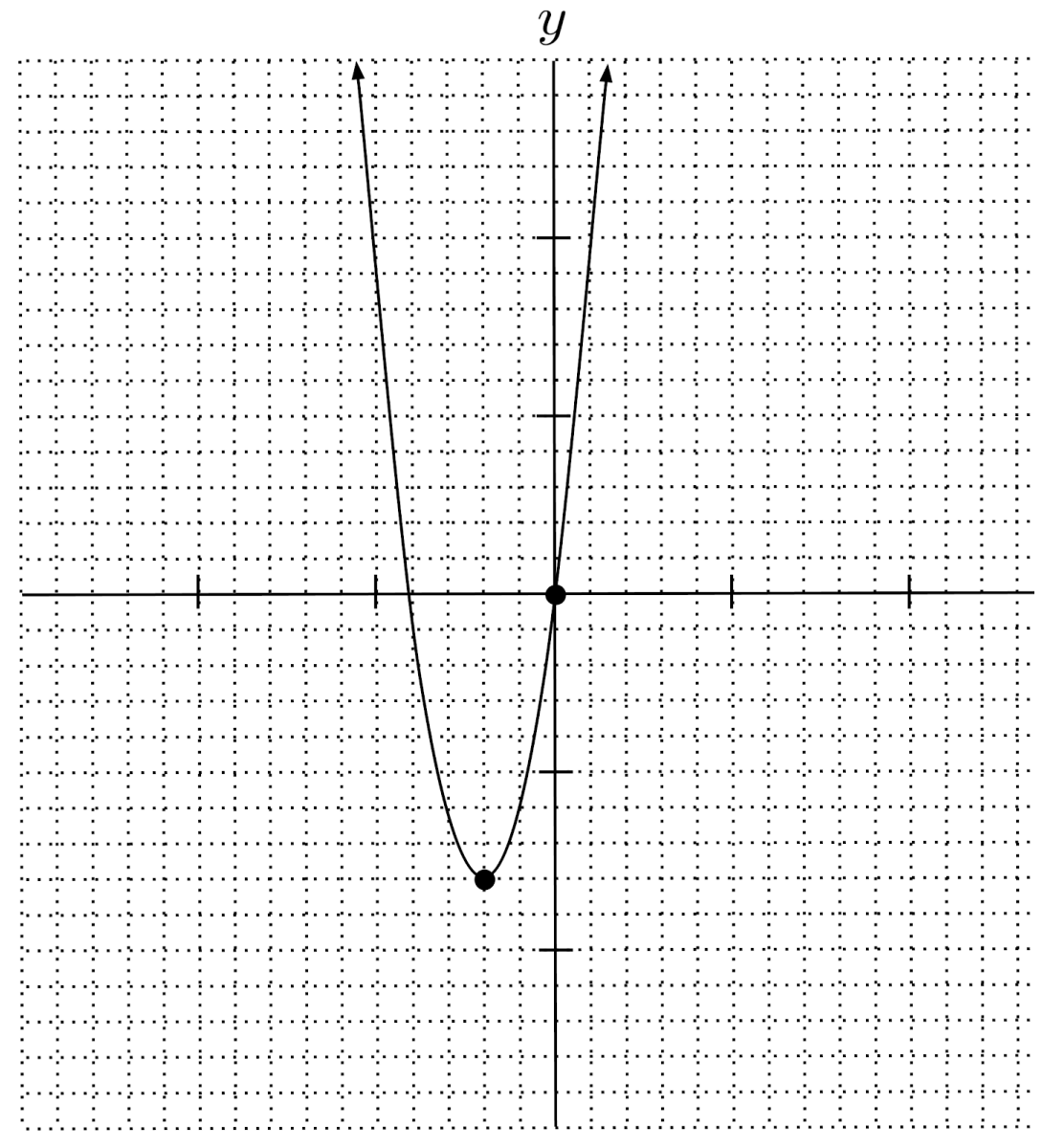
$5) \hspace{.5cm} y=9x-3(x^2+1)-1$

Solution:
$y=-3x^2+9x-4$
$\text{down} \hspace{.5cm} \left( \frac{3}{2}, \frac{11}{4} \right) \hspace{.5cm} -4$

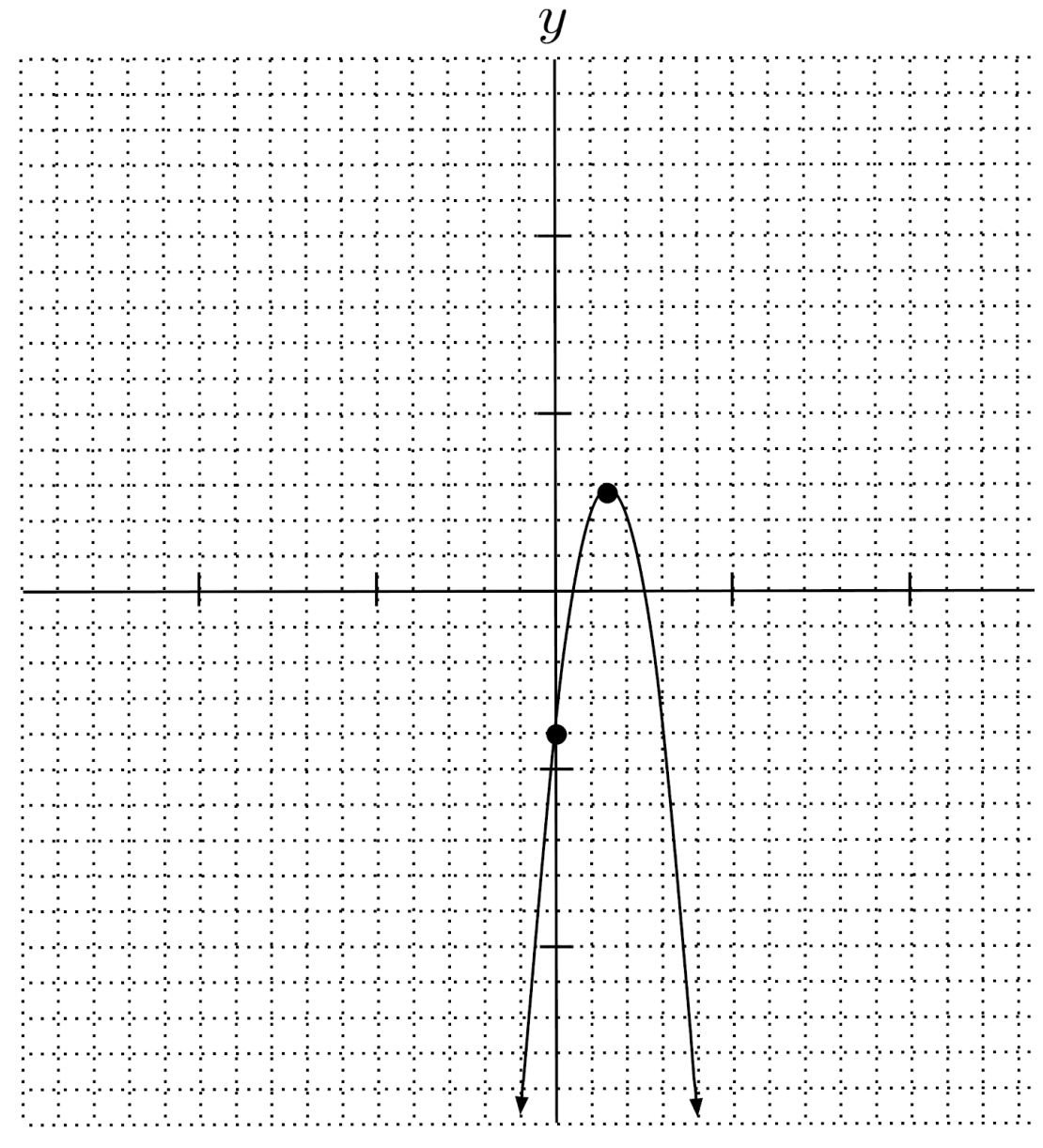
$6) \hspace{.5cm} y=4-5x(x+1)$

Solution:
$y=-5x^2-5x+4$
$\text{down} \hspace{.5cm} \left( -\frac{1}{2}, \frac{21}{4} \right) \hspace{.5cm} 4$

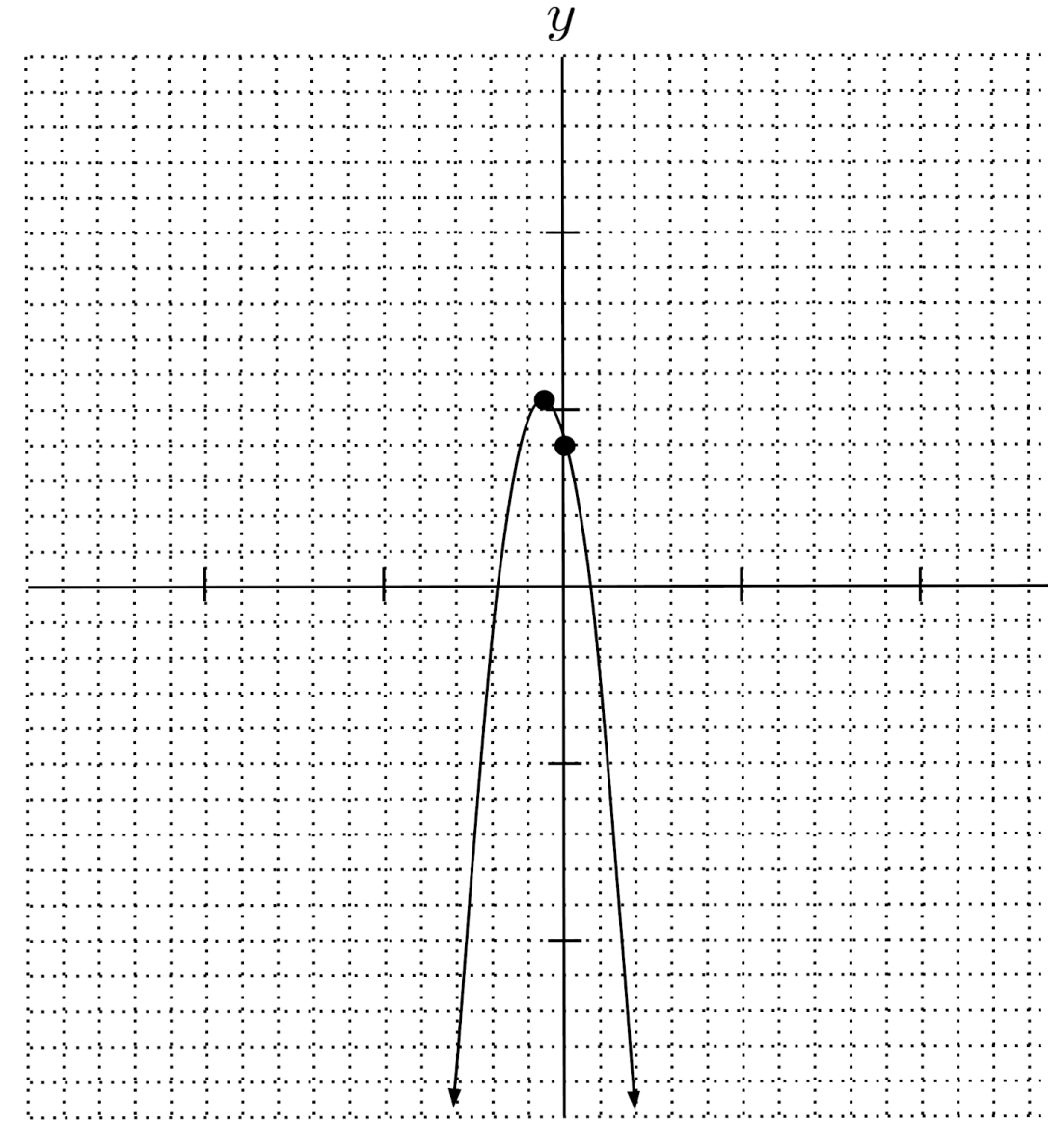
$7) \hspace{.5cm} y-6x-2=x(x+1)$

Solution:
$y=x^2+7x+2$
$\text{up} \hspace{.5cm} \left( -\frac{7}{2}, -\frac{41}{4} \right) \hspace{.5cm} 2$

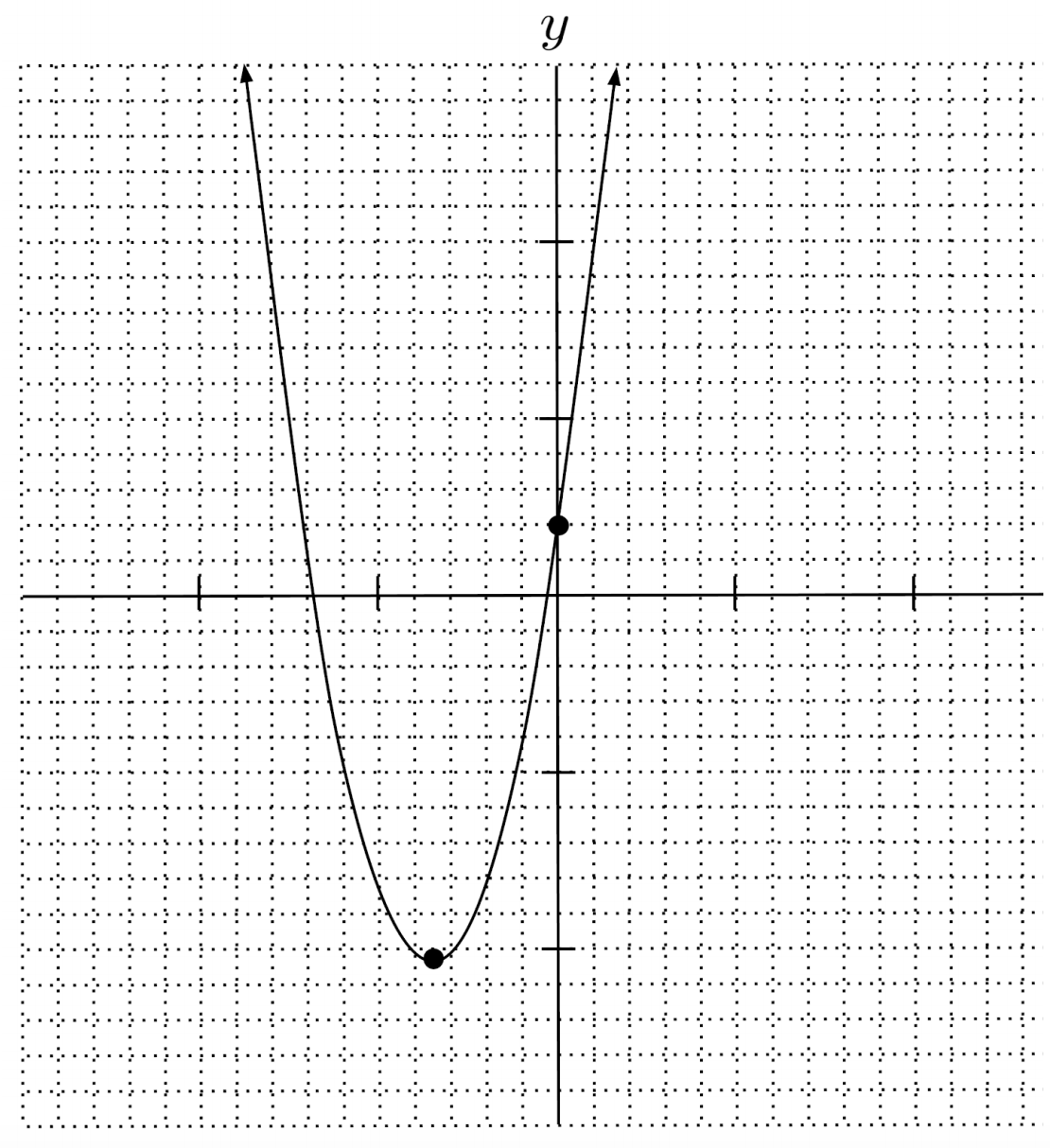
$8) \hspace{.5cm} 10x+y=10x(x+2)$

Solution:
$y=10x^2+10x$
$\text{up} \hspace{.5cm} \left( -\frac{1}{2}, -\frac{5}{2} \right) \hspace{.5cm} 0$

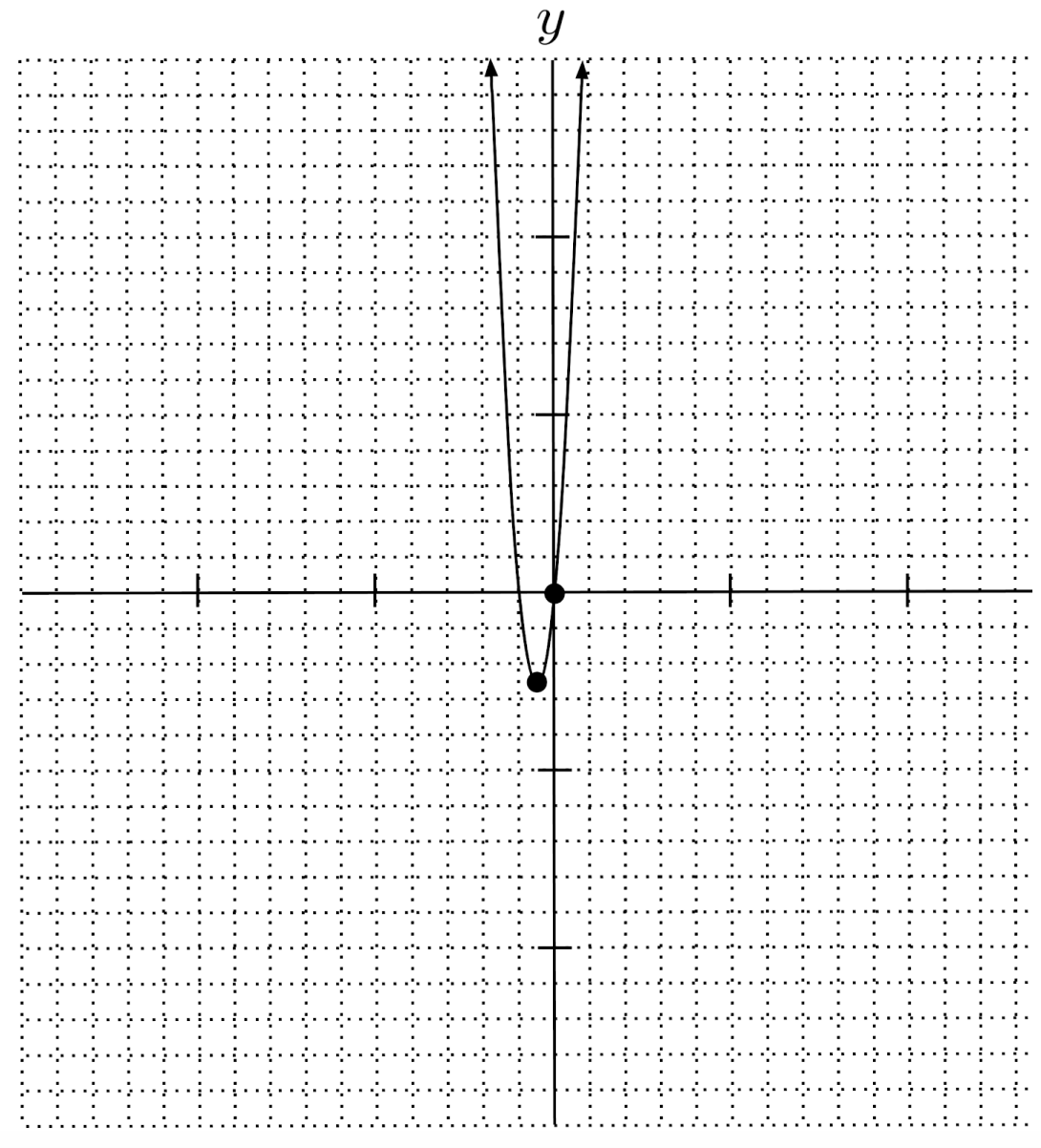
$9) \hspace{.5cm} 3(y-x^2-4x)=13+2y$

Solution:
$y=3x^2+12x+13$
$\text{up} \hspace{.5cm} (-2,1) \hspace{.5cm} 13$

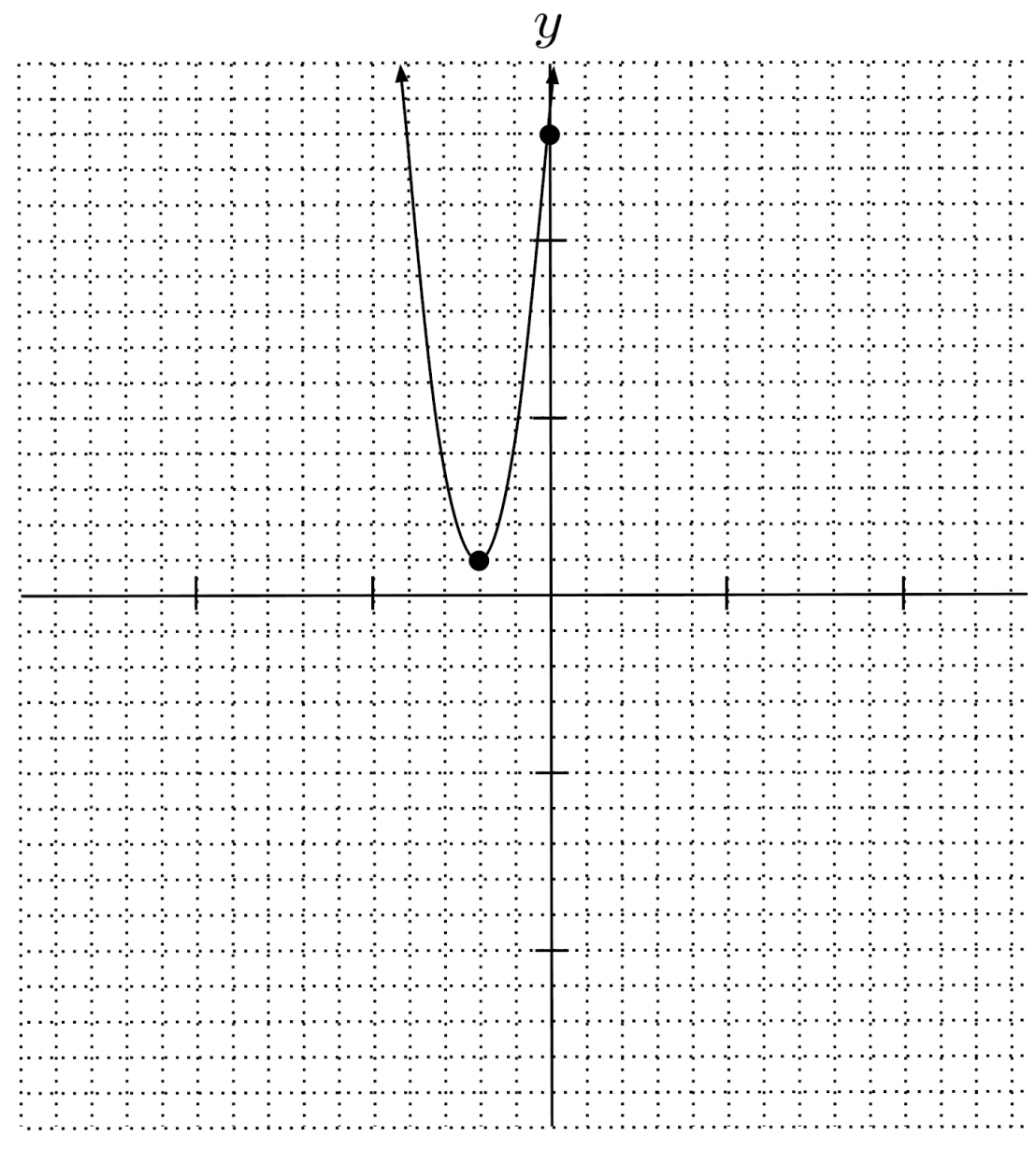
$10) \hspace{.5cm} x(3x+4)=1-y$

Solution:
$y=-3x^2-4x+1$
$\text{up} \hspace{.5cm} \left( -\frac{2}{3}, \frac{7}{3} \right) \hspace{.5cm} 1$

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Standard Form of a Quadratic Equation. In Justin Math: Algebra. https://justinmath.com/standard-form-of-a-quadratic-equation/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.