Rescalings of Functions

by Justin Skycak (@justinskycak) on July 02, 2018

When a function is rescaled, it is stretched or compressed along one of the axes, like a slinky.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Rescalings of Functions. In Justin Math: Algebra. https://justinmath.com/rescalings-of-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

When a function is rescaled, it is stretched or compressed along one of the axes, like a slinky. The function’s general shape is preserved, but it might look a bit thinner or fatter afterwards.

Rescalings Outside the Function

Rescalings occur when a constant term is multiplied in a function. When the constant term is multiplied on the outside of a function, the function stretches or compresses along the y-axis.

For example, multiplying outside by $3$ with the transformation

$f(x)=\sin x \rightarrow f(x)=3\sin x$

stretches the function outward vertically, away from the x-axis.

On the contrary, multiplying outside by $\frac{1}{3}$ with the transformation

$f(x)=\sin x \rightarrow f(x)=\frac{1}{3} \sin x$

compresses the function inward vertically, towards the x-axis.

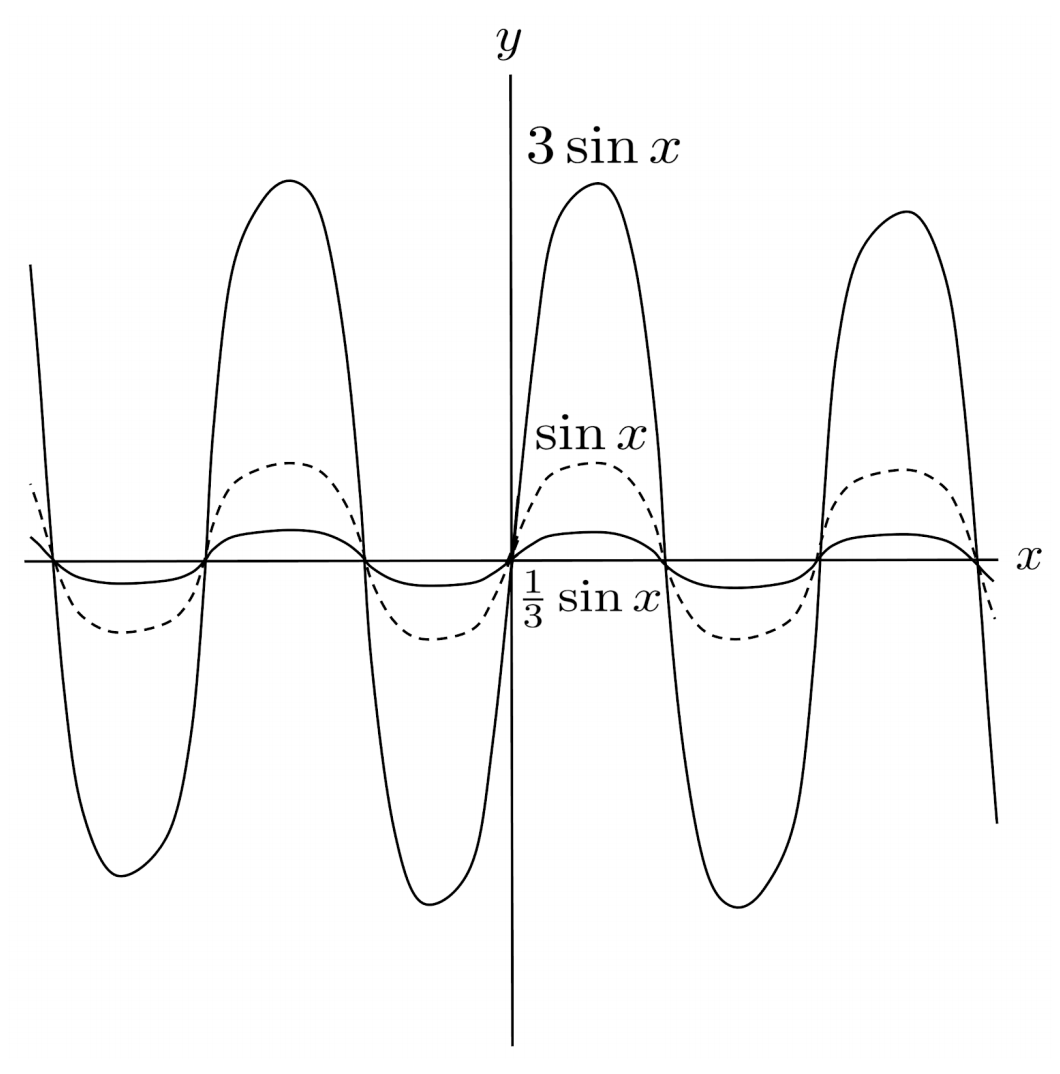
Rescalings Inside the Function

On the other hand, when the constant term is multiplied on the inside of a function, the function stretches or compresses horizontally along the x-axis.

For example, multiplying inside by $3$ with the transformation

$f(x)=\sin x \rightarrow f(x)= \sin 3x$

compresses the function inward horizontally, towards the y-axis.

On the contrary, multiplying inside by $\frac{1}{3}$ with the transformation

$f(x)=\sin x \rightarrow f(x)= \sin \frac{1}{3}x$

stretches the function outward horizontally, away from the y-axis.

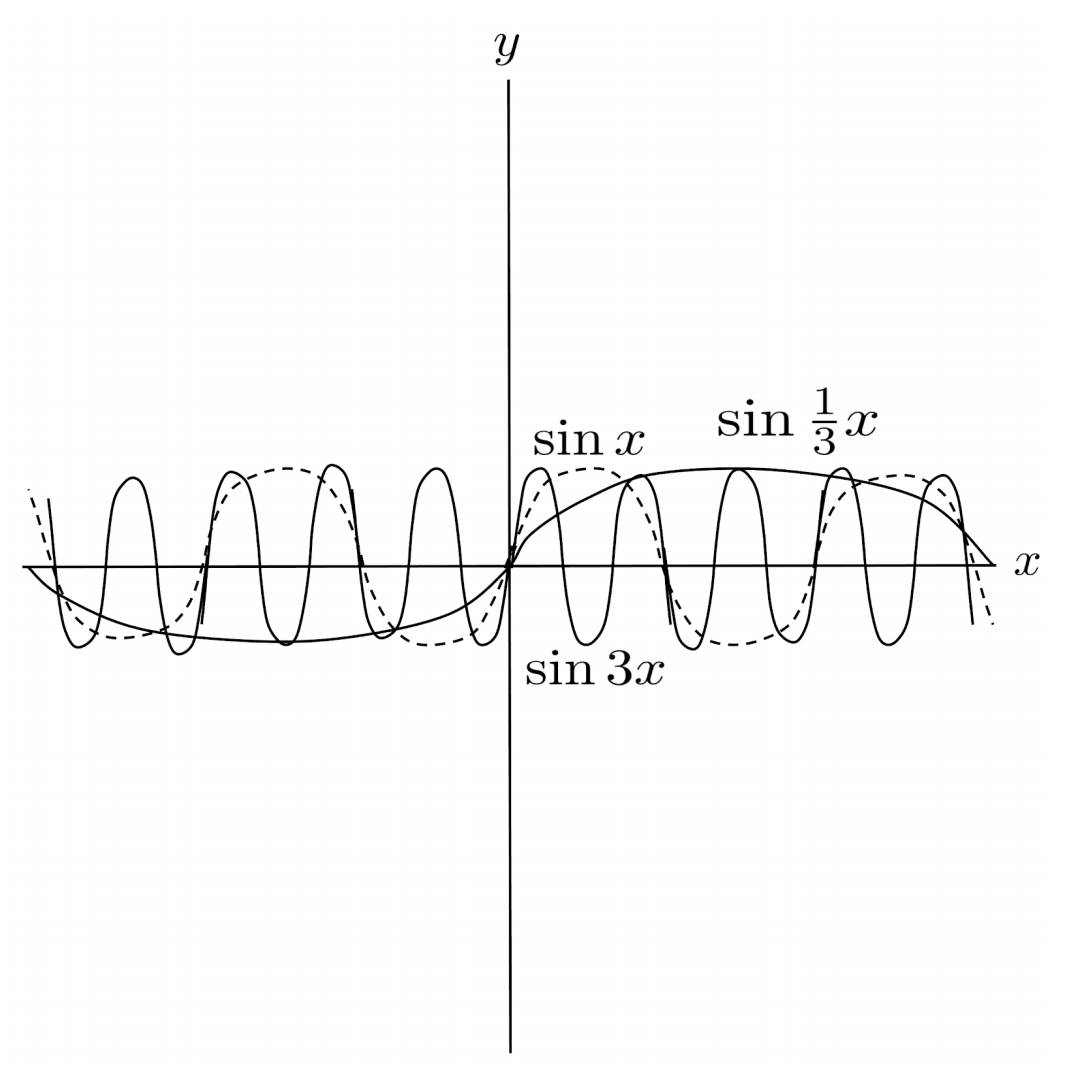
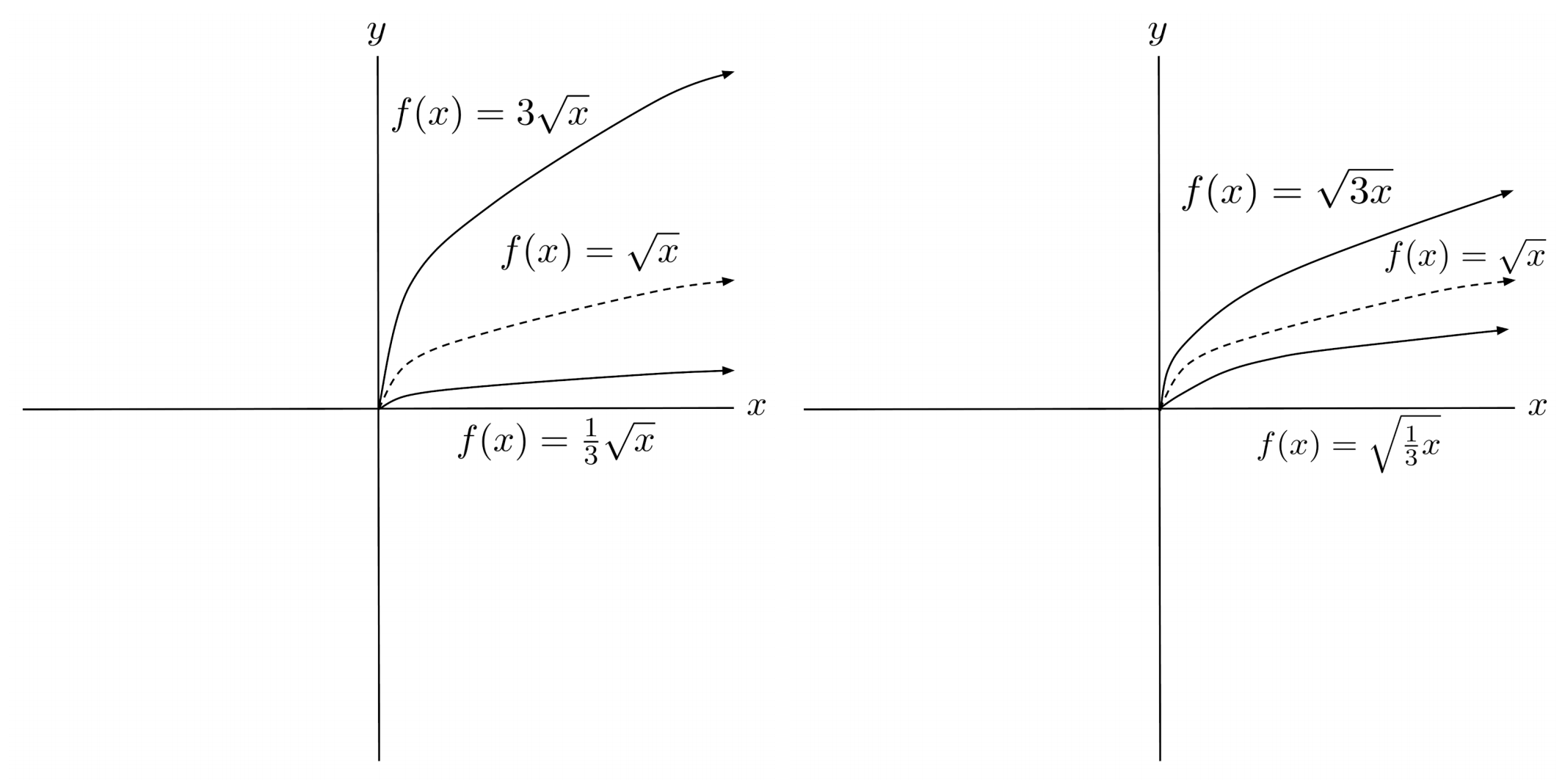
For functions that are more linear than curvy, such as $f(x)=\sqrt{x}$, vertical and horizontal rescalings can have similar effects on the graph.

Intuition

Similar to vertical shifts, vertical rescalings are very intuitive: if we multiply a function by a number, every output of the function is multiplied by that number.

If the number is greater than $1$, every output y-value is increased by the multiplier. If the number is less than $1$, every output y-value is decreased by the multiplier.

Similar to horizontal shifts, the intuition behind horizontal rescalings is not as straightforward. Multiplying a BIG number inside a function COMPRESSES it, rather than stretching it.

Think about it this way: when we transform $f(x)=\sqrt{x}$ into $f(x)=\sqrt{3x}$, the output originally at $x=3$ is now at $x=1$, because $\sqrt{3}$ is the same as $\sqrt{3(1)}$. Similarly, the output originally at $x=1$ is now at $x=\frac{1}{3}$, because $\sqrt{1}$ is the same thing as $\sqrt{ 3 \left( \frac{1}{3} \right) }$. Every input needs to be divided by $3$, to keep its output the same.

Combining Rescalings and Shifts

When we have both vertical and horizontal rescalings, it doesn’t matter which we perform first.

However, when dealing with rescalings and shifts simultaneously, it’s important to perform horizontal shifts first, then rescalings, and lastly vertical shifts. This way, horizontal shifts are themselves rescaled, and vertical shifts are not.

To see why horizontal shifts themselves need to be rescaled, consider the function transformation of $f(x)=x$ into $f(x)=\sqrt{3x-1}$.

In the original function, we have $\sqrt{1}=1$. If we rescale first and then shift $1$ right, then the input $x=1$ is rescaled to $x=\frac{1}{3}$ and shifted to $x=\frac{4}{3}$.

When we input the transformed input into the transformed function, it should produce the same result as the original input in the original function – but this is not the case for $x=\frac{4}{3}$.

$\sqrt{ 3 \left( \frac{4}{3} \right) - 1 } = \sqrt{3} \neq 1$

On the other hand, if we first shift $1$ right and then rescale, then the input $x=1$ is shifted to $x=2$ and rescaled to $x=\frac{2}{3}$.

Indeed, $x=\frac{2}{3}$ produces the same result as the original input in the original function.

$\sqrt{ 3 \left( \frac{2}{3} \right) - 1 } = \sqrt{1} = 1$

Exercises

Use rescalings (followed by shifts) to graph the following functions. (You can view the solution by clicking on the problem.)

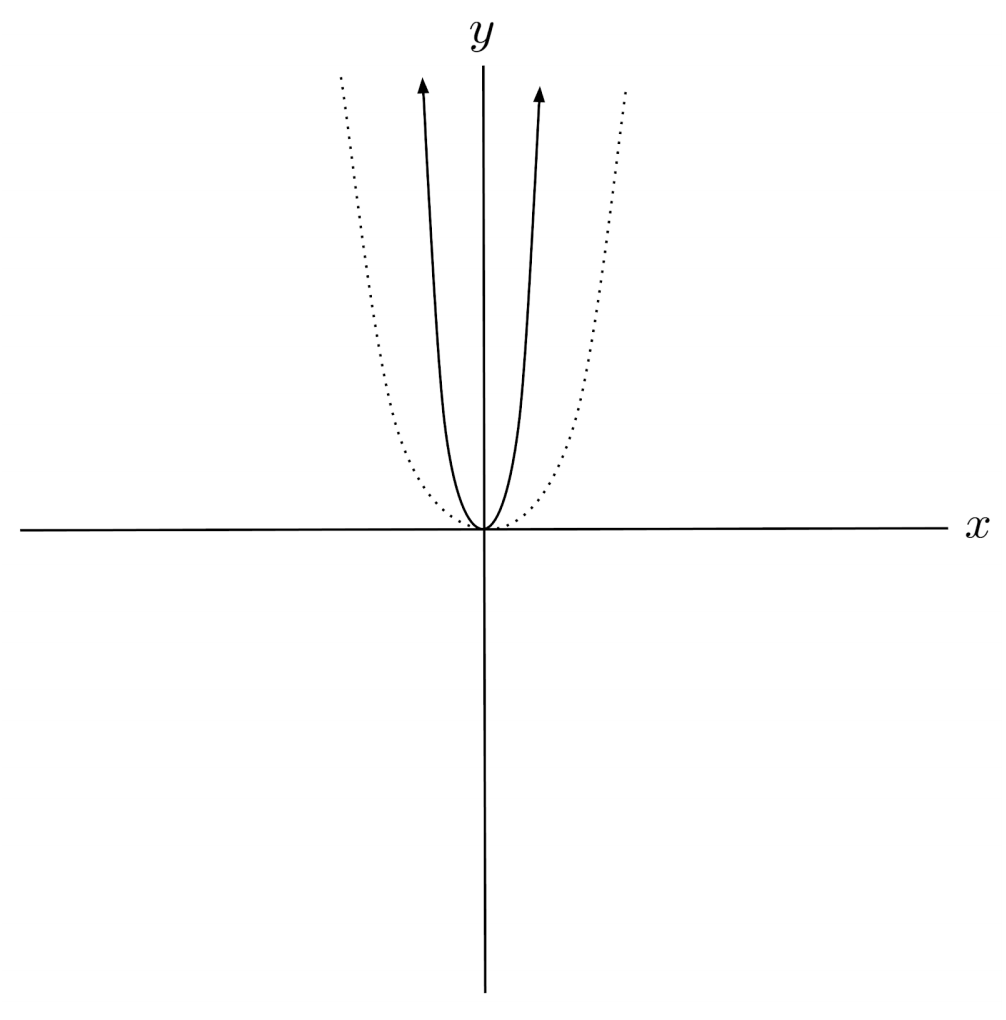
$1) \hspace{.5cm} f(x)= 3x^2$

Solution:

$2) \hspace{.5cm} f(x)= \left( \frac{1}{2} x \right)^2$

Solution:

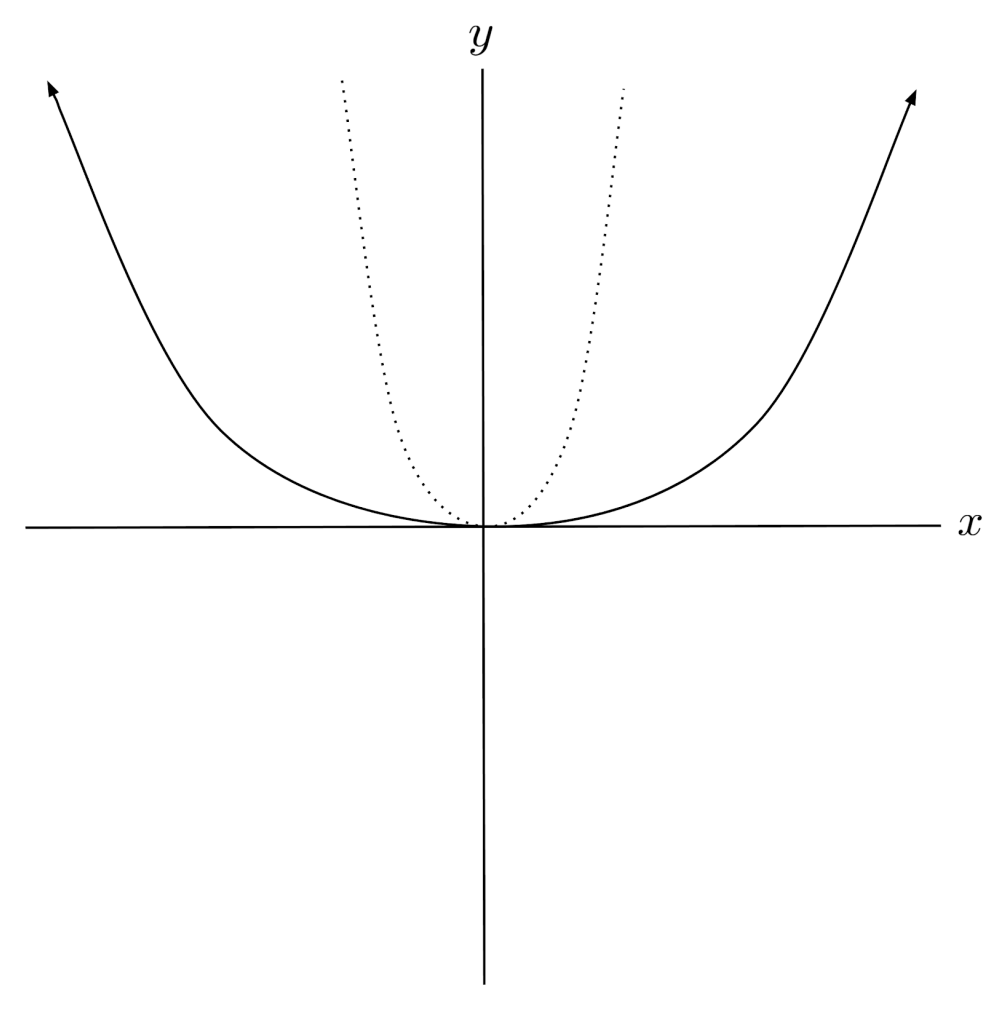
$3) \hspace{.5cm} f(x)= \frac{1}{4} x^3$

Solution:

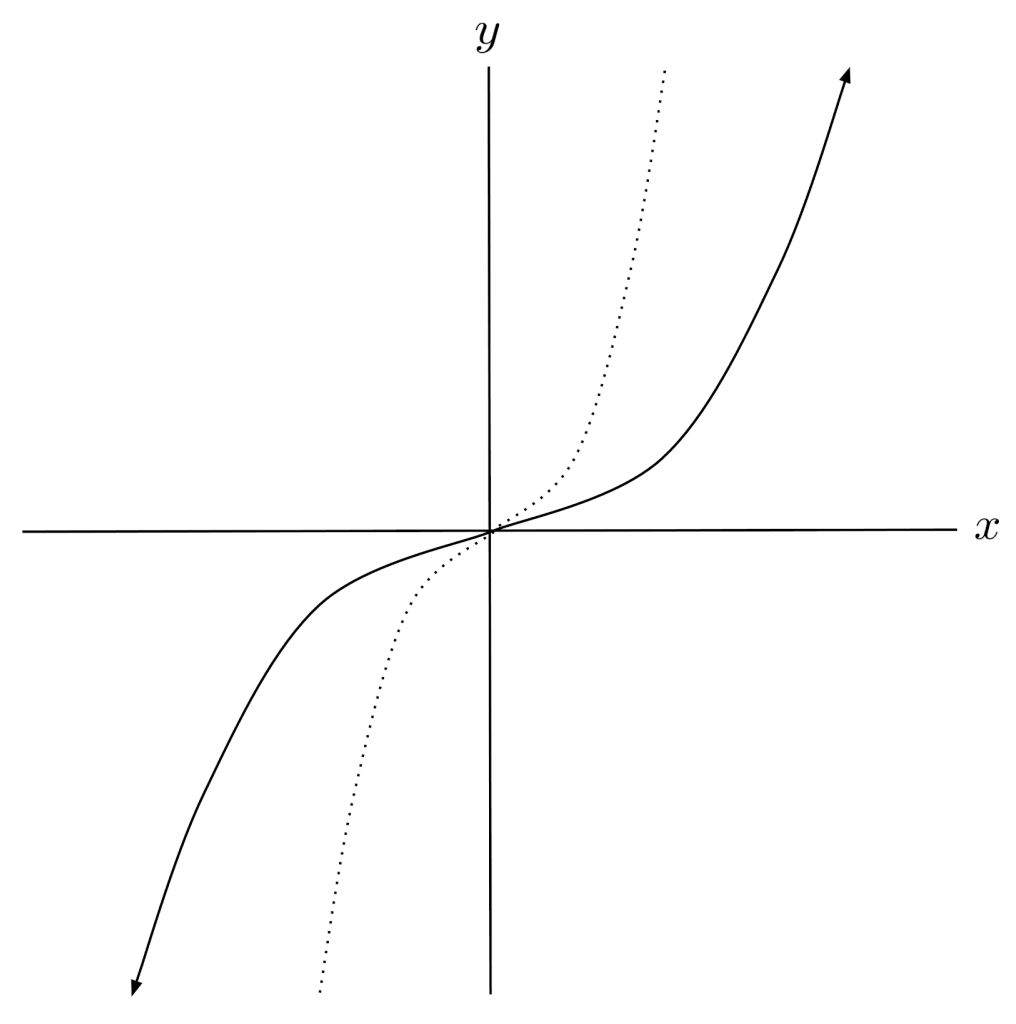
$4) \hspace{.5cm} f(x)= (2x)^3$

Solution:

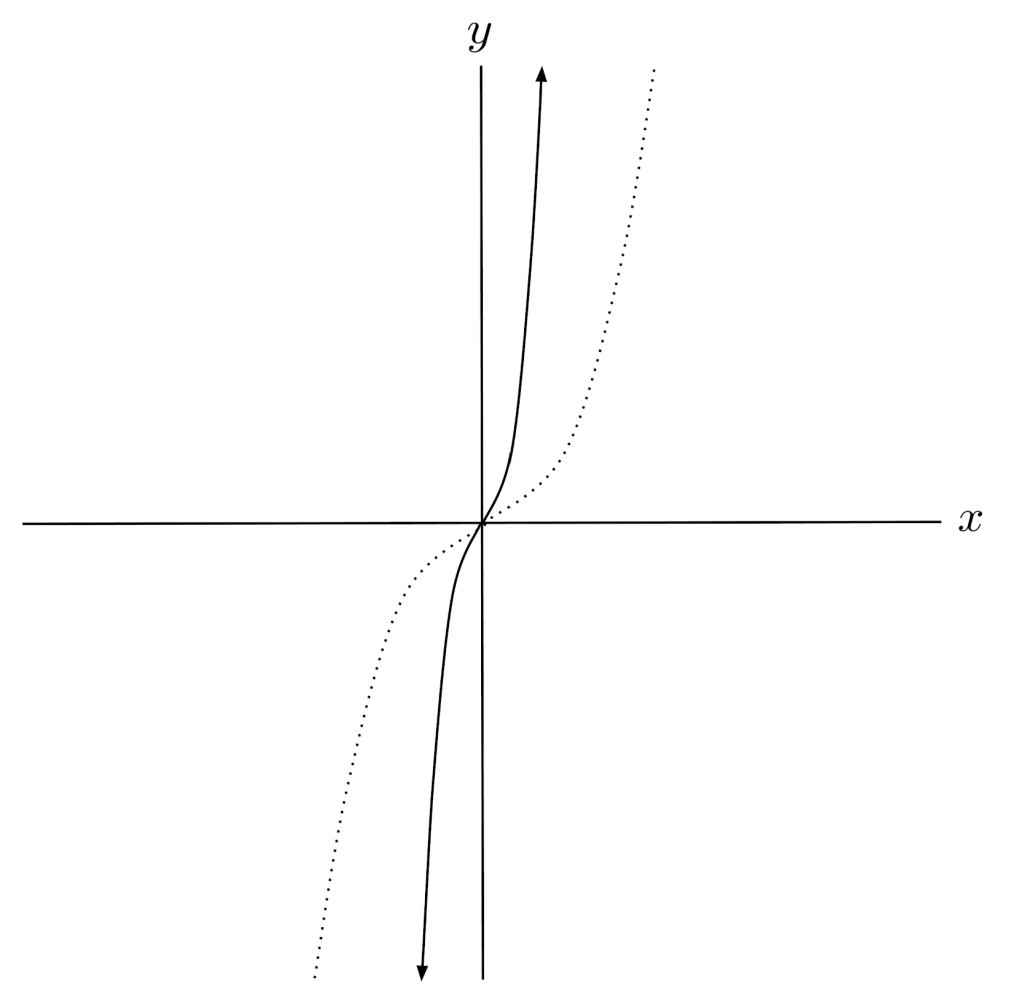
$5) \hspace{.5cm} f(x)= 4 \sqrt{x}$

Solution:

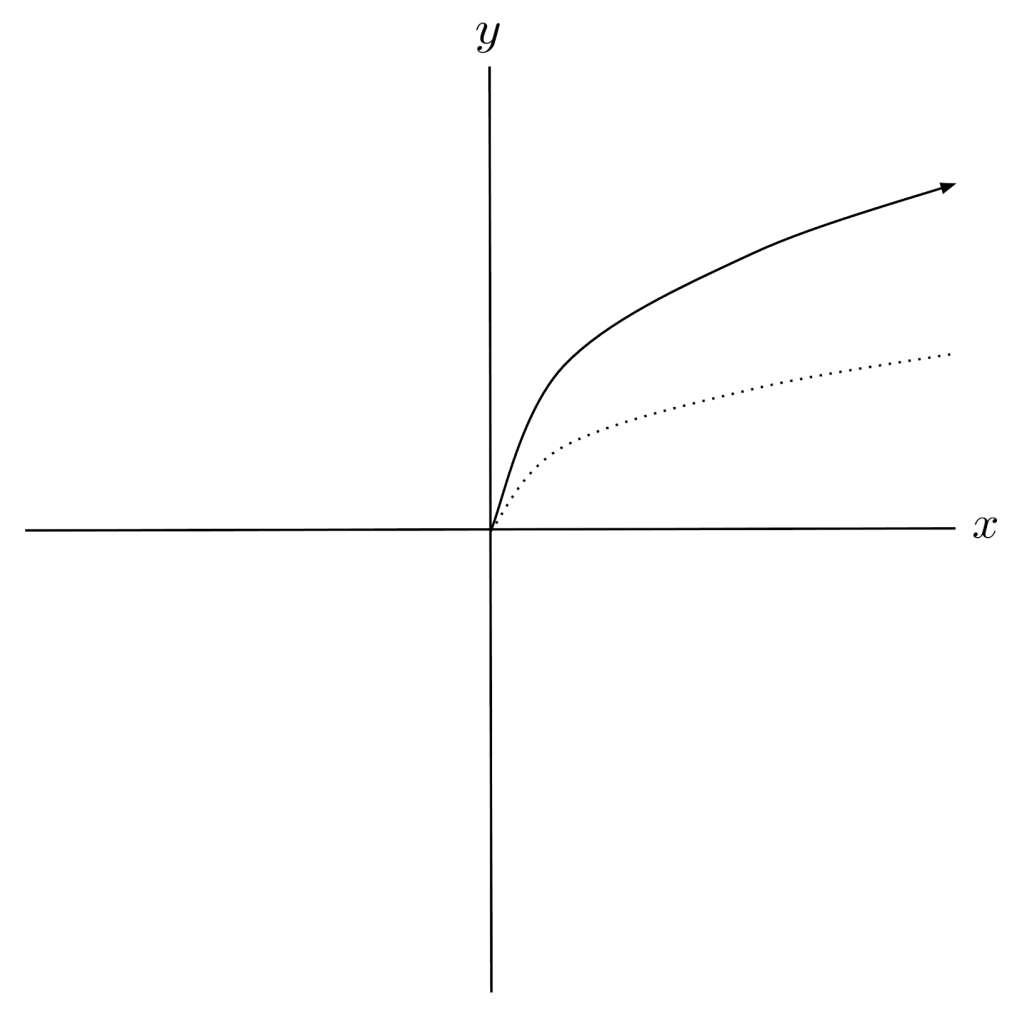
$6) \hspace{.5cm} f(x)= \sqrt[3]{5x}$

Solution:

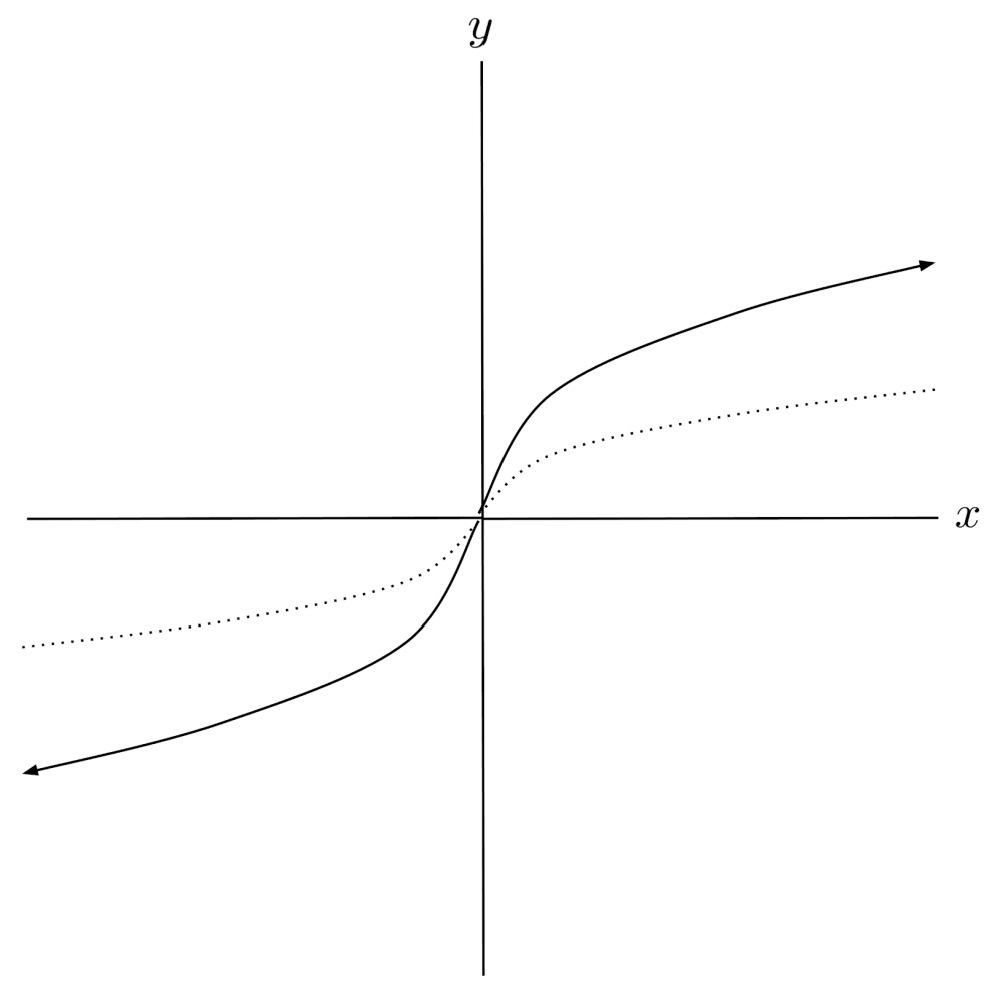
$7) \hspace{.5cm} f(x)= 4^{\frac{1}{2} x}$

Solution:

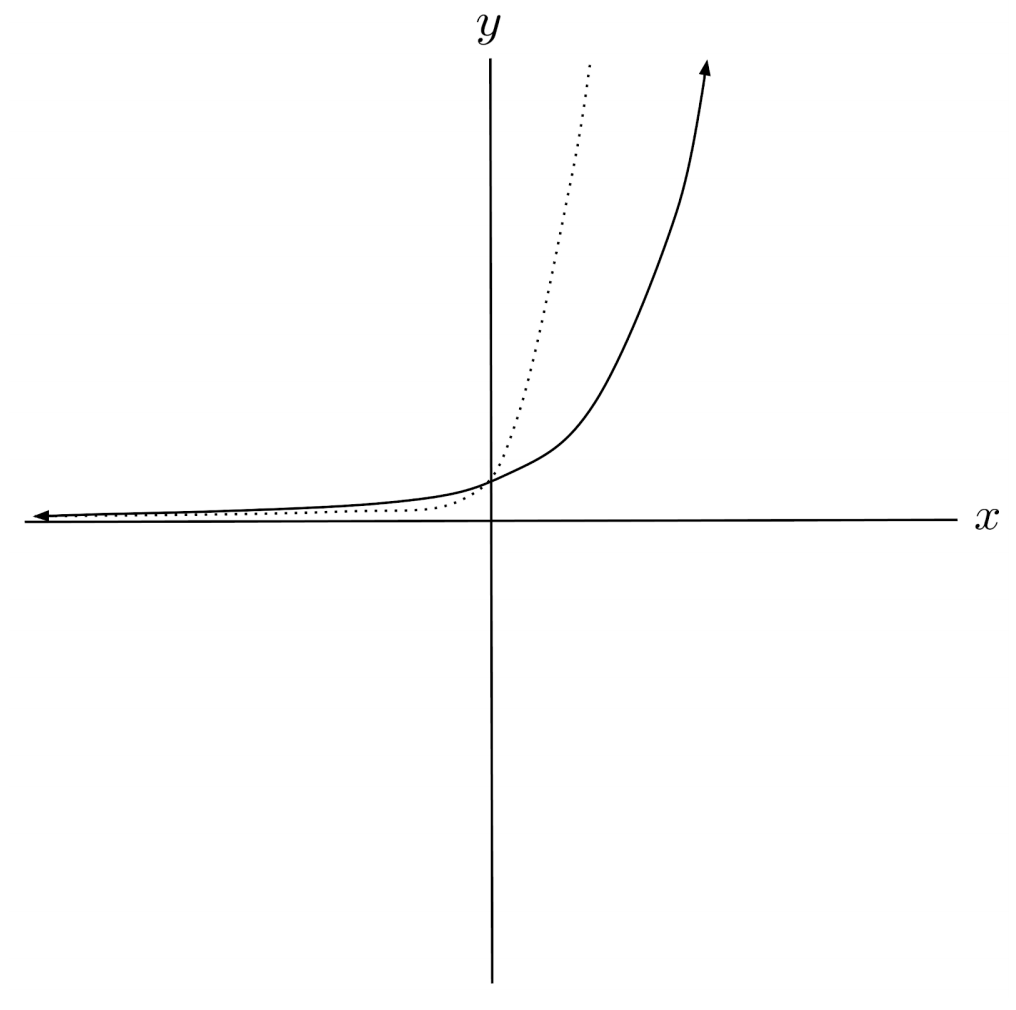
$8) \hspace{.5cm} f(x)= 3 \left( \frac{1}{2} \right)^x$

Solution:

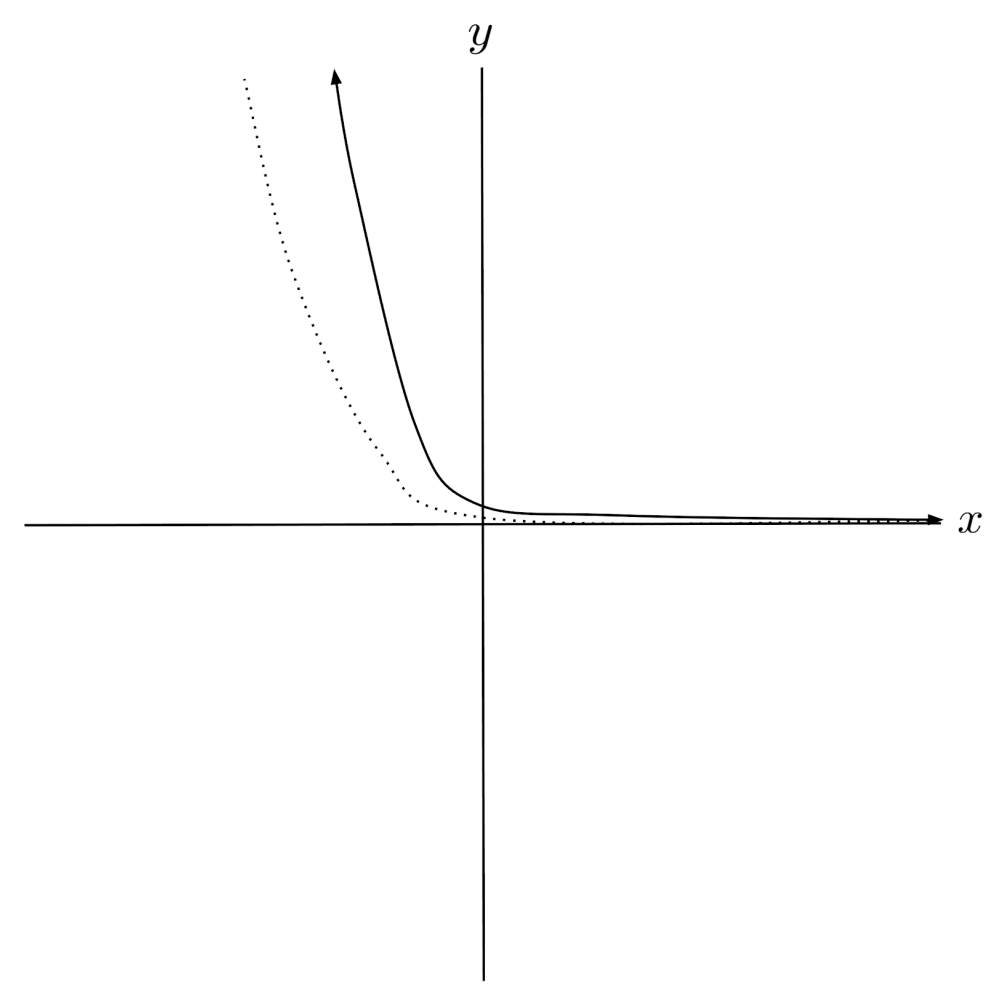
$9) \hspace{.5cm} f(x)=4 \sin x$

Solution:

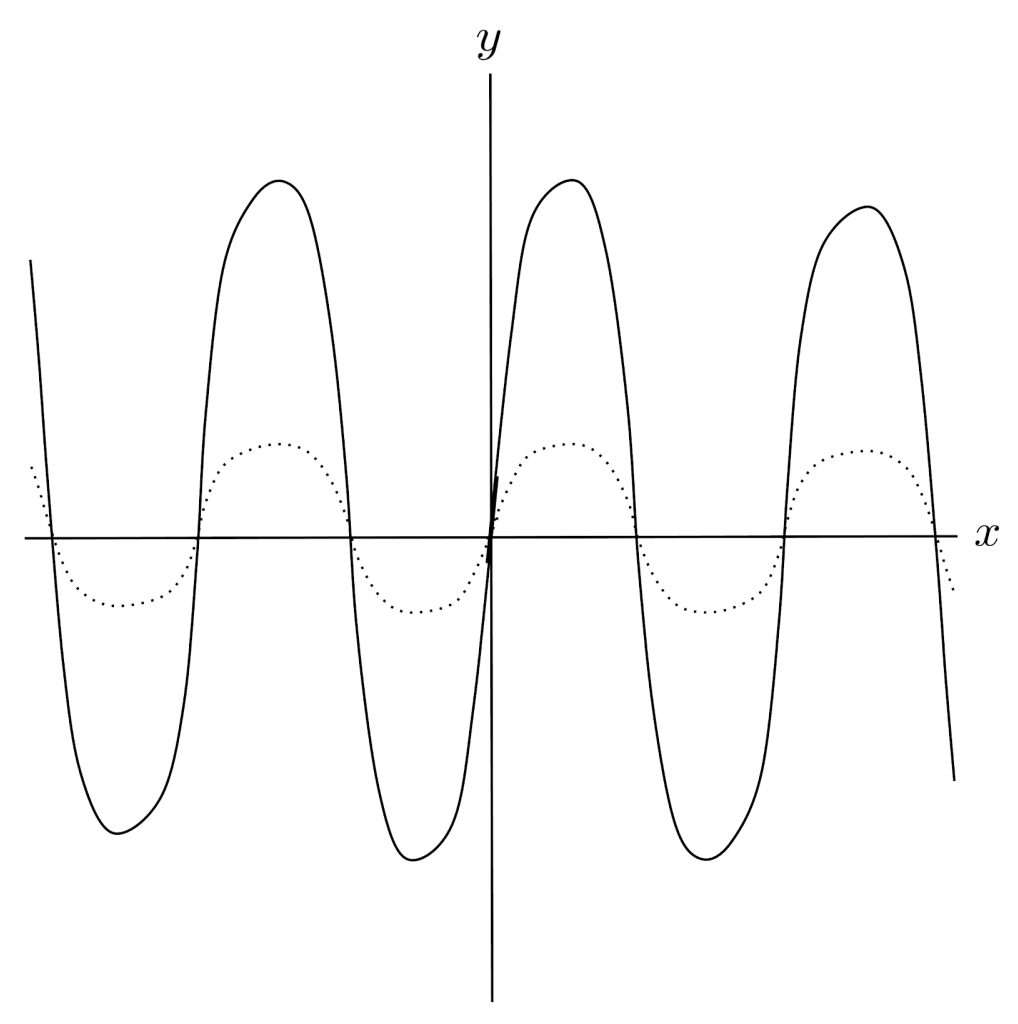
$10) \hspace{.5cm} f(x)=\tan \left( \frac{1}{3} x \right)$

Solution:

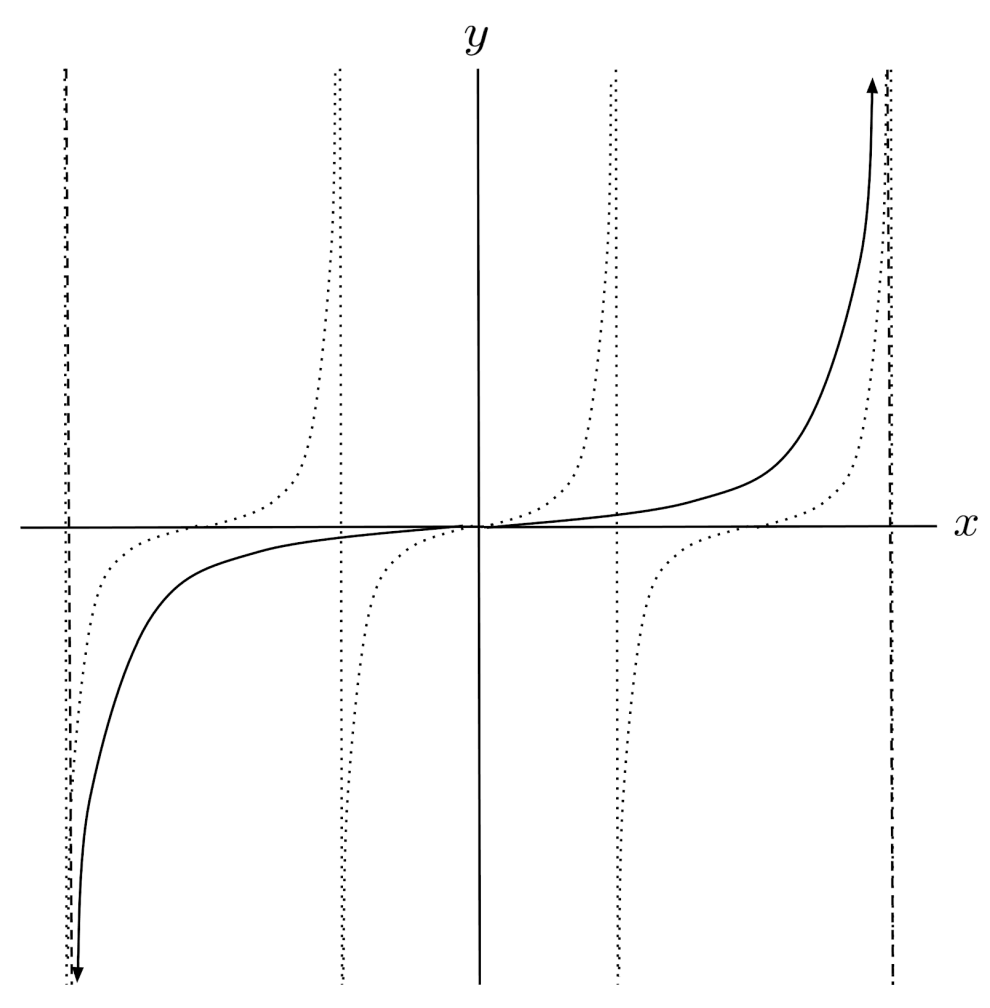
$11) \hspace{.5cm} f(x)= \left| \frac{1}{2} x + 3 \right|$

Solution:

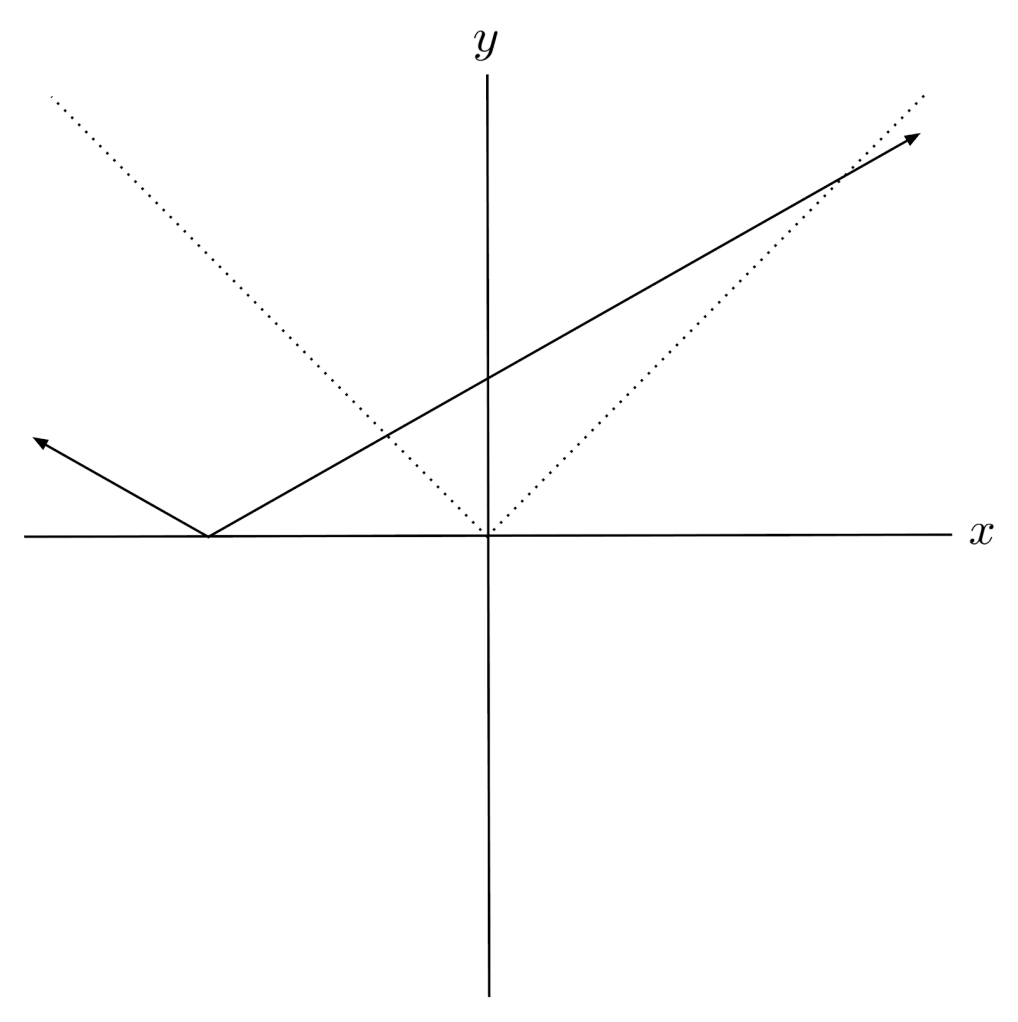
$12) \hspace{.5cm} f(x)= 4 |x-2| - 7$

Solution:

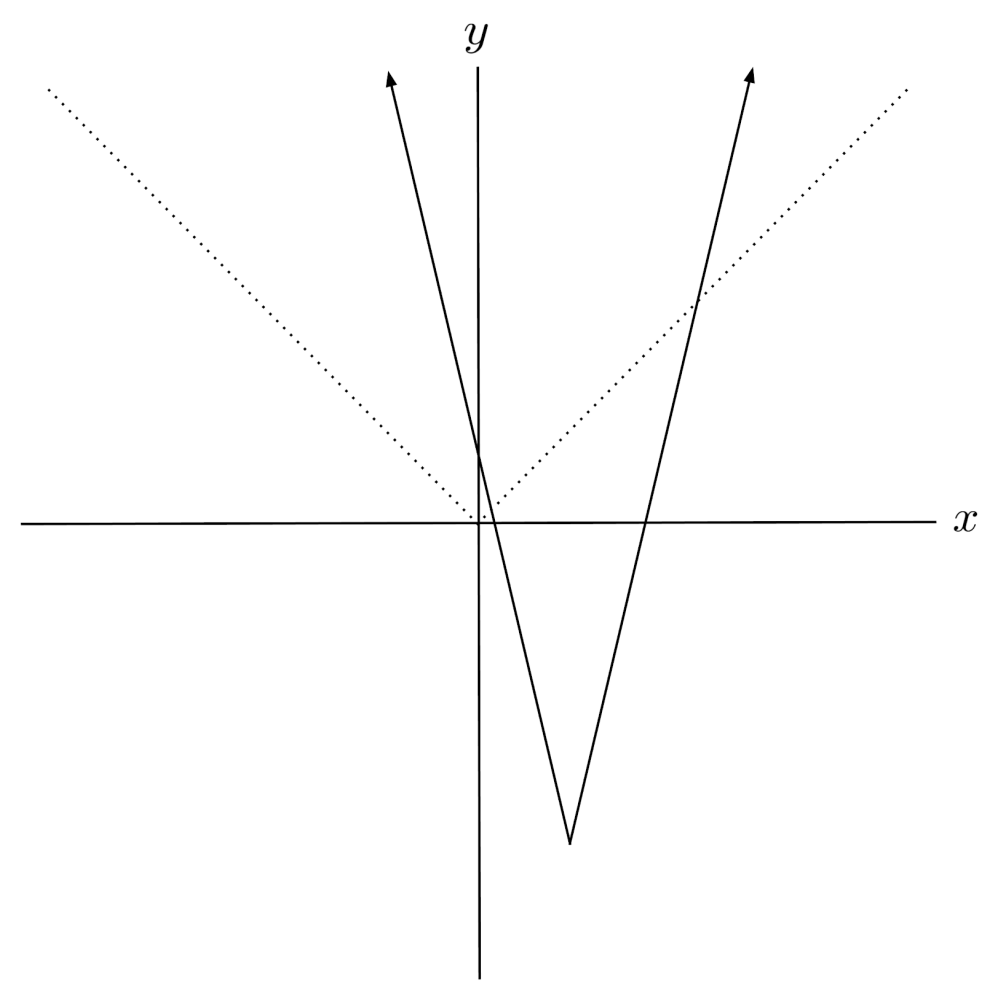
$13) \hspace{.5cm} f(x)= 2(4)^{\frac{1}{2}x-2}$

Solution:

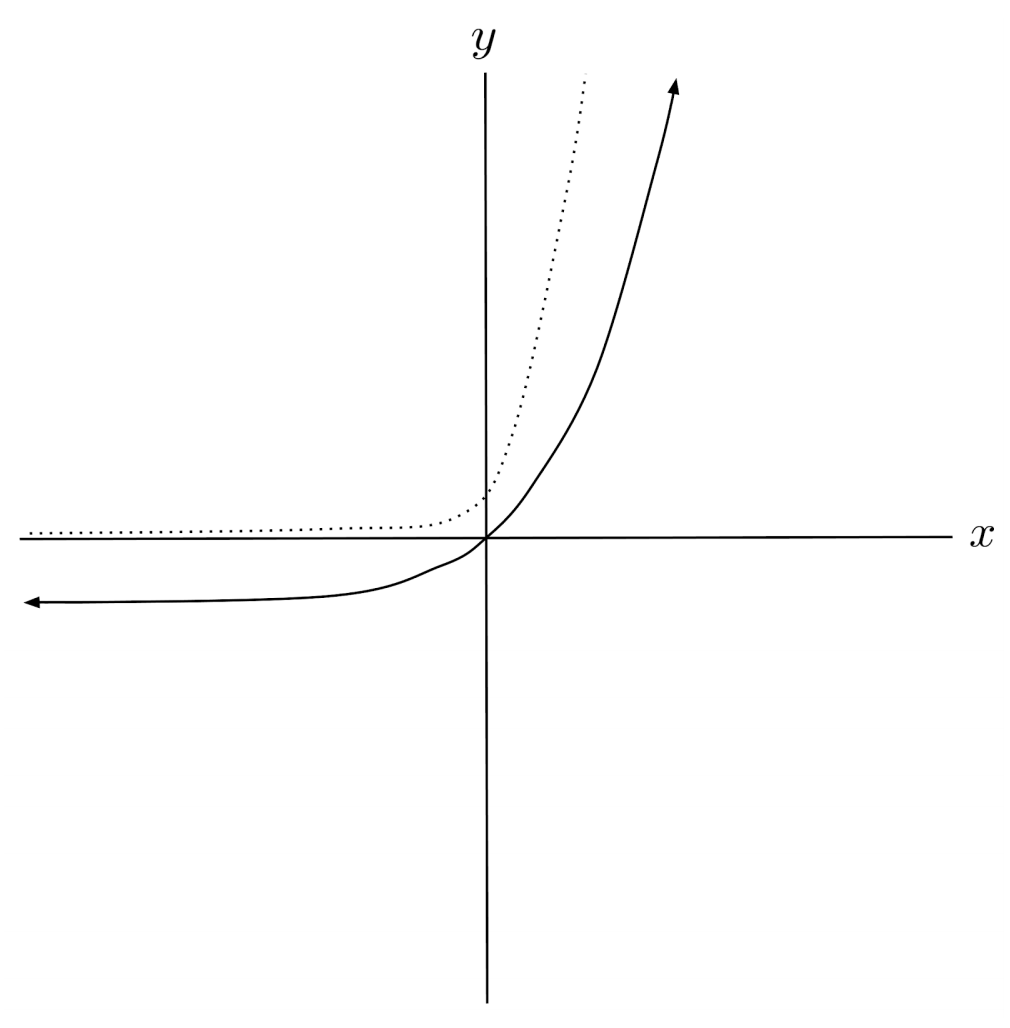
$14) \hspace{.5cm} f(x)=8\cos \left( \frac{1}{4}x+2 \right)+3$

Solution:

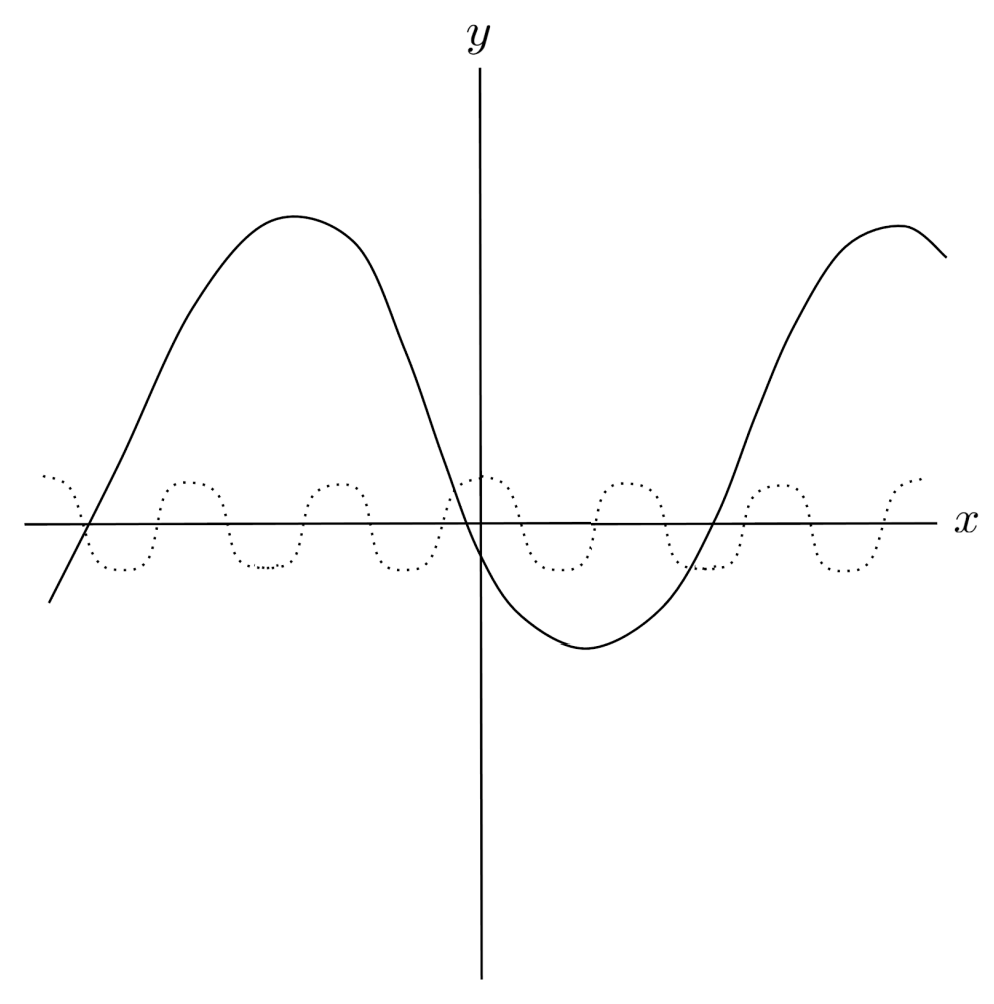
$15) \hspace{.5cm} f(x)= 5 \sqrt[3]{7x-3}-5$

Solution:

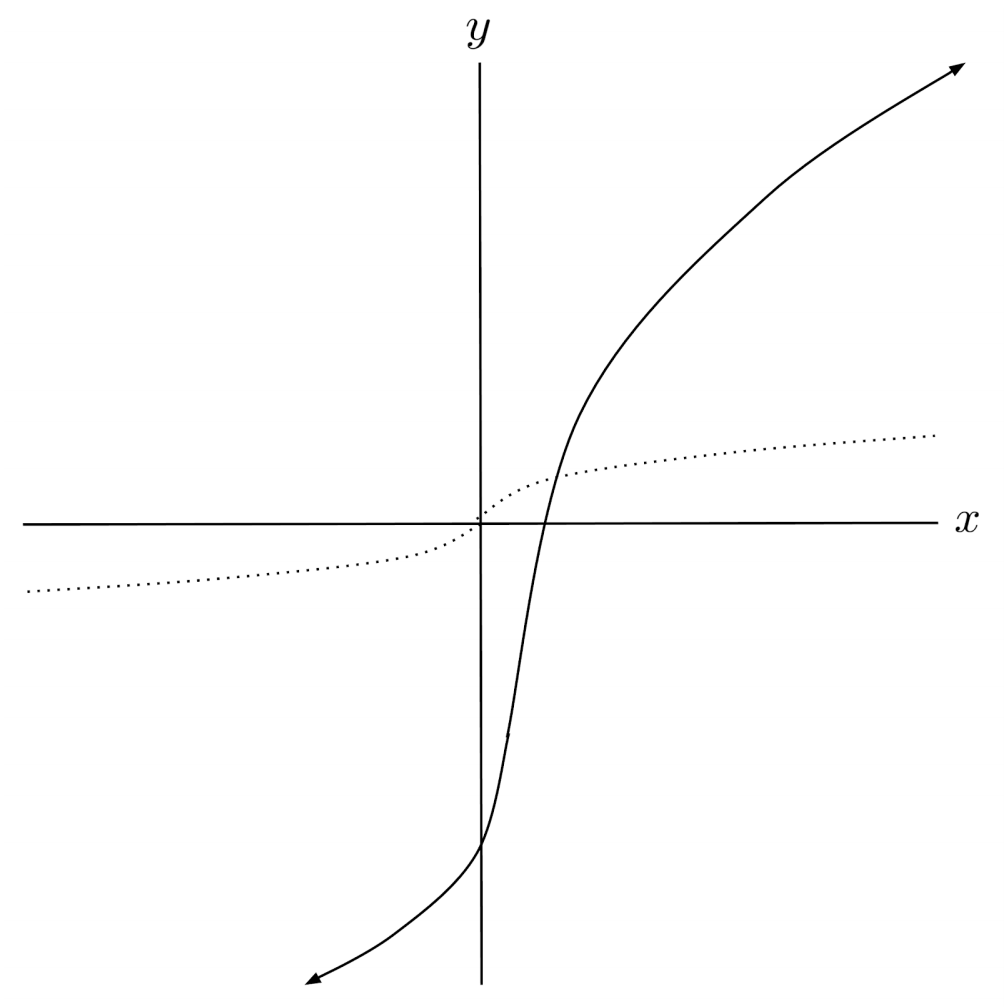
$16) \hspace{.5cm} f(x)= \frac{1}{8} (4x-4)^2-5$

Solution:

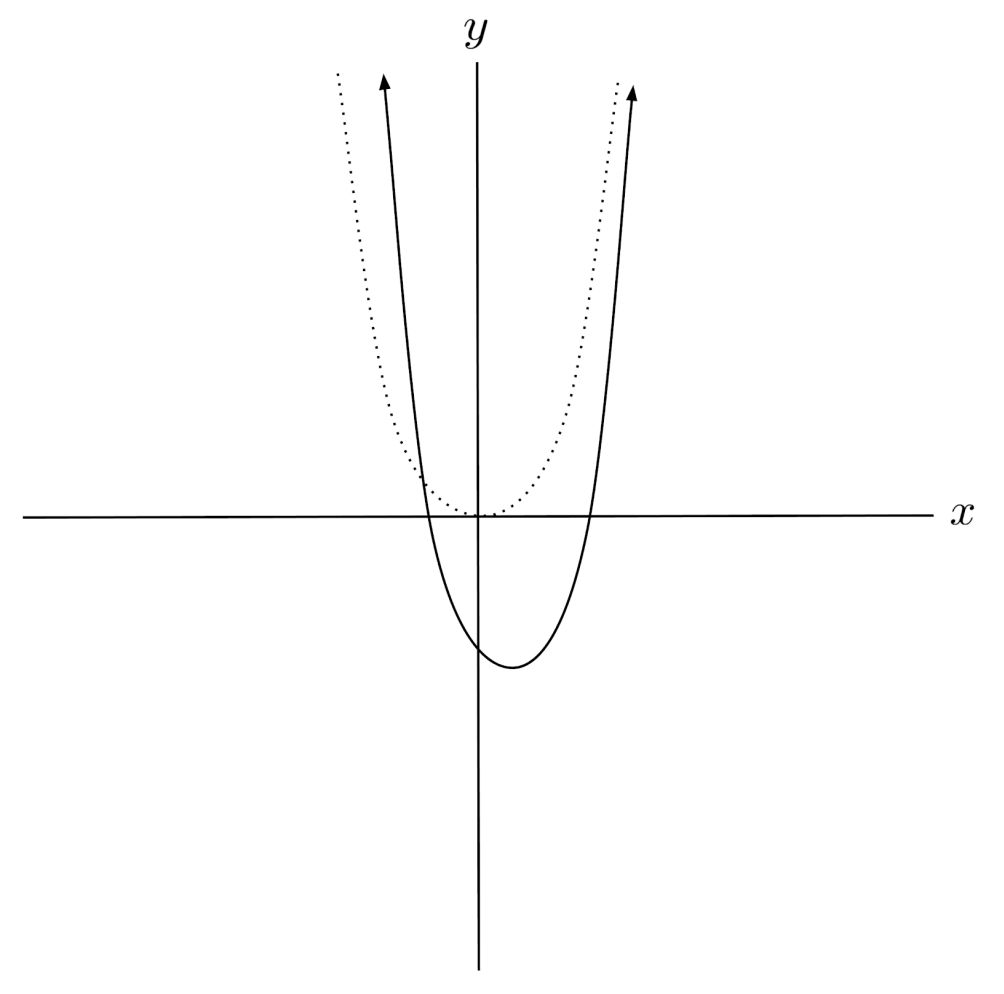
This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Rescalings of Functions. In Justin Math: Algebra. https://justinmath.com/rescalings-of-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.