Radical Functions

Radical functions involve roots: square roots, cube roots, or any kind of fractional exponent in general.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Radical Functions. In Justin Math: Algebra. https://justinmath.com/radical-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

A radical function is a function that involves roots: square roots, cube roots, or any kind of fractional exponent in general. We can often infer what their graphs look like by sandwiching them between polynomial functions.

For example, the radical function $f(x)=\sqrt{x^3}$ can be written as $f(x)=x^{3/2}$, and its exponent $\frac{3}{2}$ is between $1$ and $2$, so the graph of $f$ lies between the graphs of $y=x$ and $y=x^2$.

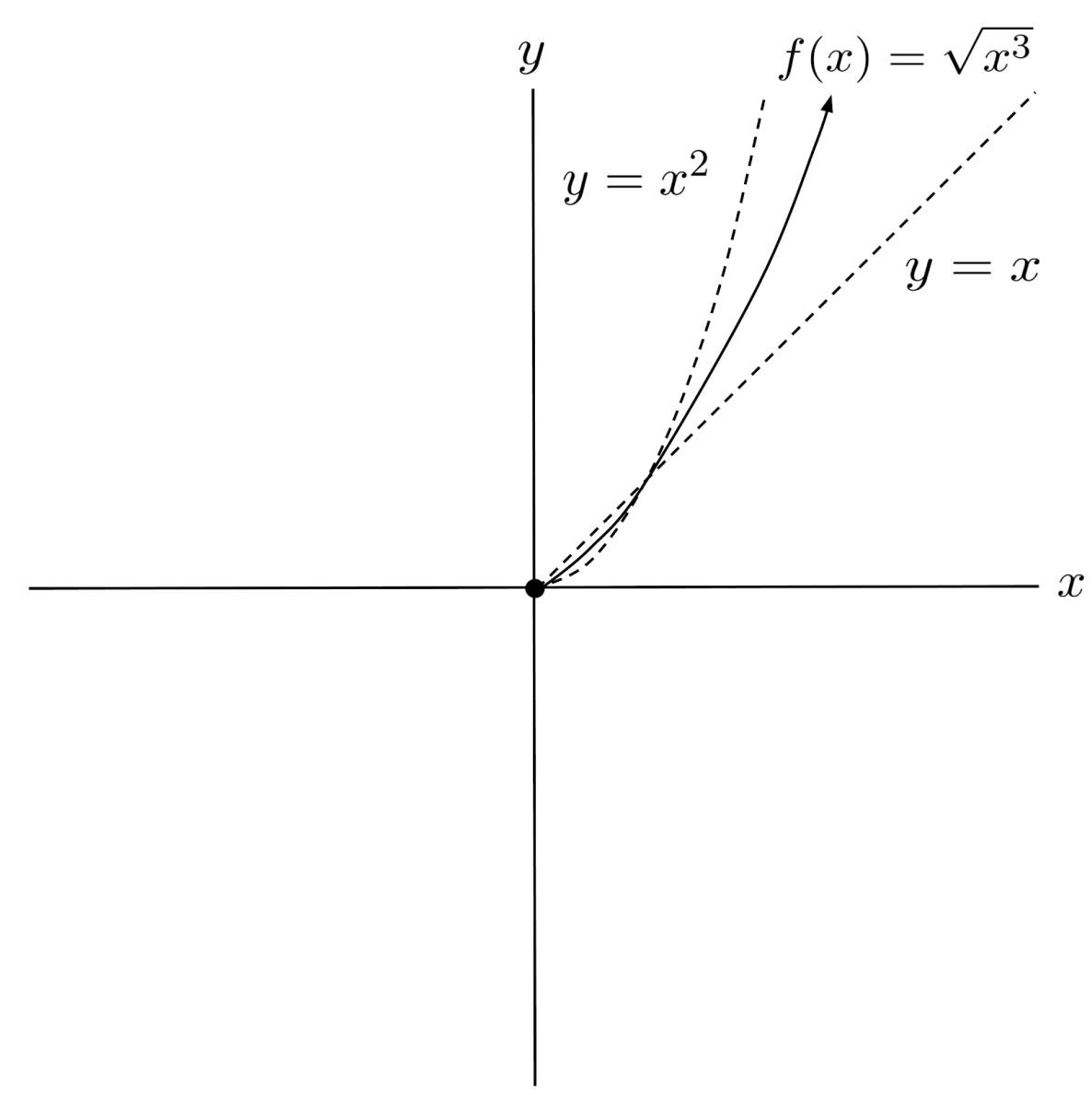
Negative Inputs

However, there is one caveat: $f(x)=\sqrt{x^3}$ is not defined for negative values of $x$. If we try to input a negative number, we end up taking the root of a negative number, which is undefined in the real numbers.

As a consequence, the graph of $f$ remains blank for negative values of $x$, left of the y-axis.

That being said, other radical functions can sometimes accept negative inputs, which are converted to positive numbers before the radical is applied.

For example, $x=-4$ is a valid input to $f(x)=\sqrt{-x}$ because the operation inside the root converts the negative input to a positive, and we can take the root of positive numbers.

But the operation also converts positive inputs to negatives, so the positive section of the graph disappears.

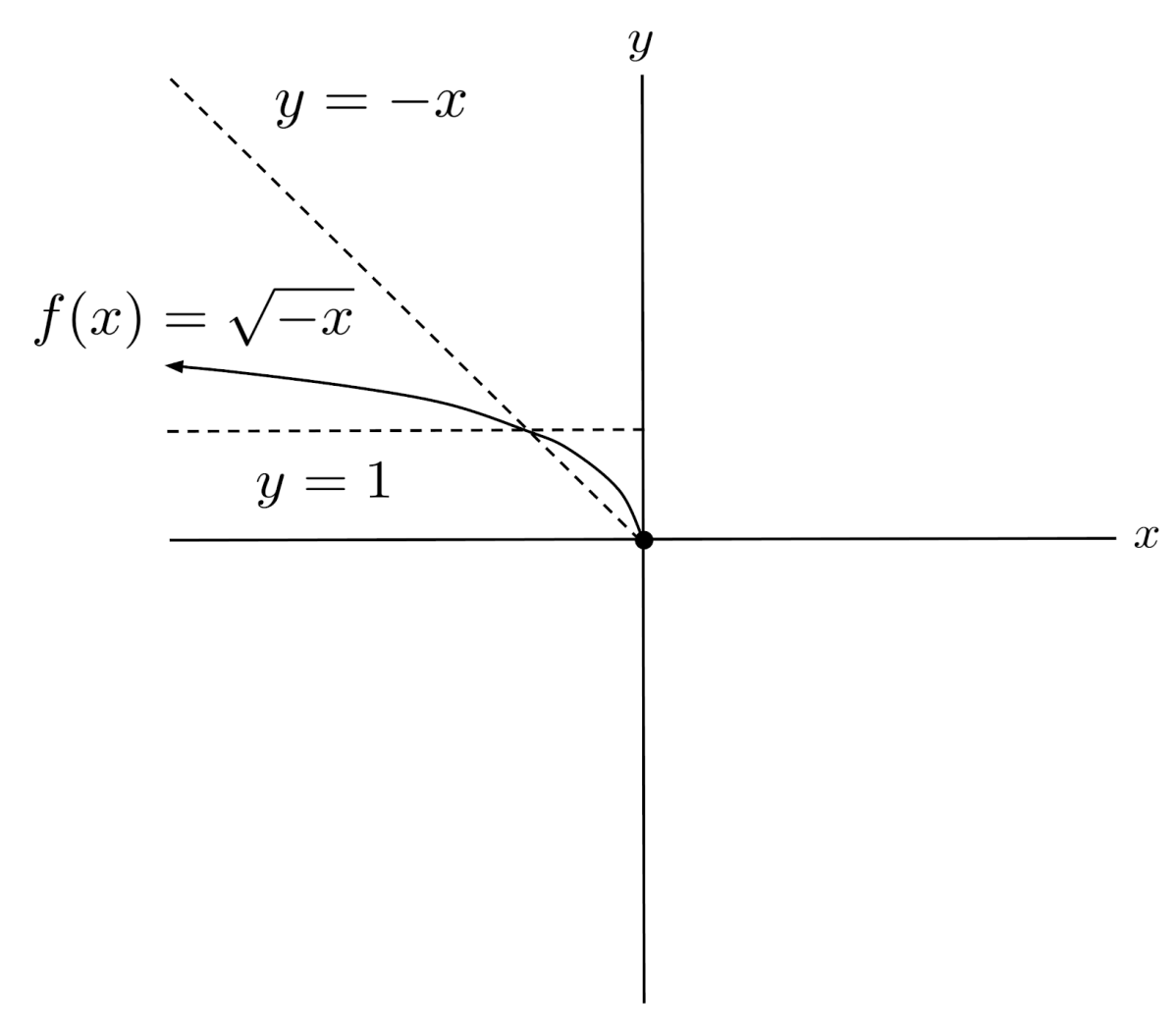
Cube Root Functions

Unlike square root functions, cube root functions like $f(x)=\sqrt[3]{x}$ can accept both positive and negative inputs because cube roots are defined for both positive and negative numbers.

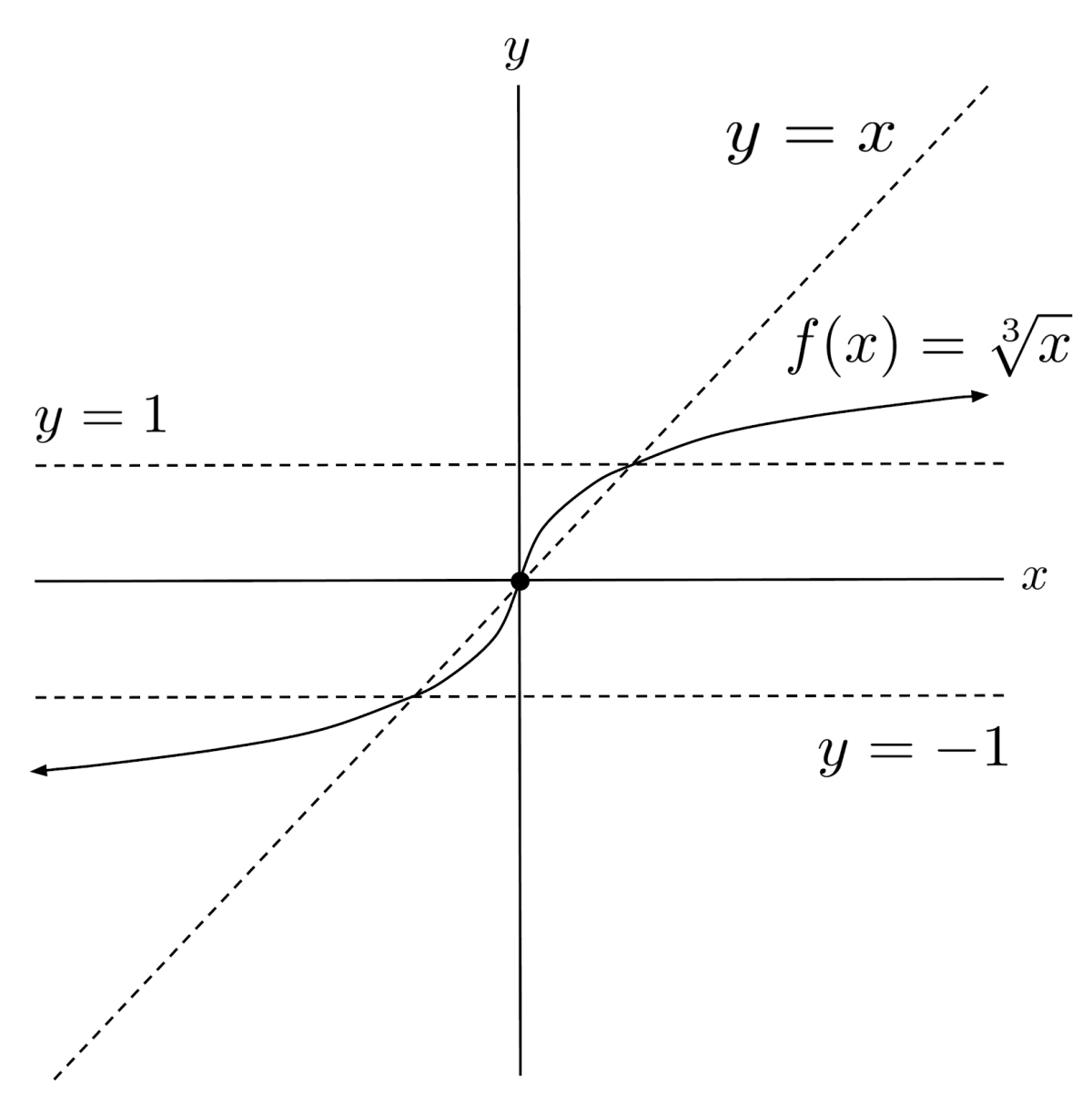
In general, whether a radical function covers the whole graph or just part of the graph depends on whether the root is an even root or an odd root.

• • Even roots are NOT defined for negative numbers, so the graph is left blank for any input $x$ that makes the inside of the root negative.
• • Odd roots ARE defined for negative numbers, so the graph exists for any input $x$, even if it makes the inside of the root negative.

Just remember that whether an x-value is a valid input to a root function does not depend solely on the sign of the x-value, but rather on what the function does to the input x-value before applying the root.

Extraneous Solutions

When solving radical equations, valid algebraic steps can sometimes lead us to solutions that aren’t actually correct.

For example, squaring both sides of the equation $\sqrt{x}=-2$ yields $x=4$. However, when we input $x=4$ into the equation to check the solution, we reach $\sqrt{4}=-2$, which simplifies to $2=-2$, which is incorrect.

Therefore, we say that the solution $x=4$ is extraneous, and the equation $\sqrt{x}=-2$ actually has no solutions in the real numbers.

Squaring both sides of an equation can introduce extraneous solutions because it introduces an additional solution that corresponds to the negative root.

It’s easiest to see this if we forget about radicals for a moment – for example, if we start with $x=2$ and square both sides, we reach $x^2=4$, which is solved by $x=\pm \sqrt{4} = \pm 2$. Squaring both sides introduced a negative solution $x=-2$, and although $-2=2$ is not true, $(-2)^2=2^2$ is true. Likewise, although $x=4$ is not a solution to $\sqrt{x}=-2$, it is a solution to $(\sqrt{x})^2=(-2)^2$ because $(2)^2=(-2)^2$.

A similar problem occurs when we raise both sides of an equation to the fourth, sixth, eighth, or any even power – raising to an even power turns negative numbers to positives, so it introduces an additional solution that corresponds to the negative root.

On the other hand, raising both sides of an equation to the third, fifth, seventh, or any odd power does not change the sign of any numbers, so it won’t lead to any extraneous solutions.

The main takeaway is that whenever we raise both sides of an equation to an even power, we need to double-check the solutions to make sure that they actually satisfy the equation.

Solving Radical Equations

In general, the best way to solve a complicated radical equation is to isolate the radical and exponentiate to cancel the radical.

When there are multiple radicals in an equation, we first need to reduce the number of radicals in the equation until there is a single radical.

We can do this by repeatedly rearranging and exponentiating both sides of the equation.

Exercises

Graph the following radical functions. (You can view the solution by clicking on the problem.)

$1) \hspace{.5cm} f(x)=\sqrt{x^5}$

Solution:

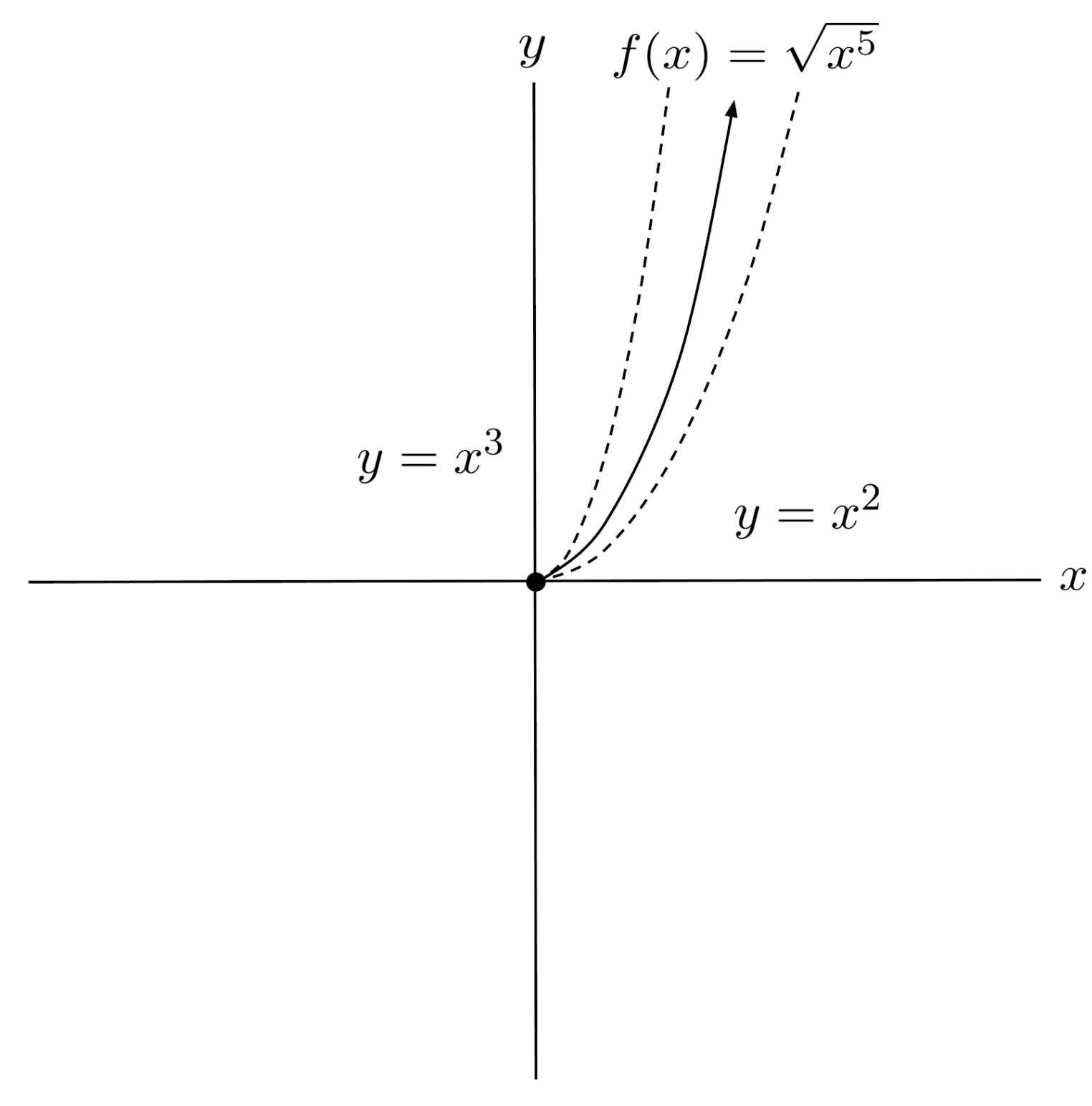
$2) \hspace{.5cm} f(x)=\sqrt[6]{x^2}$

Solution:

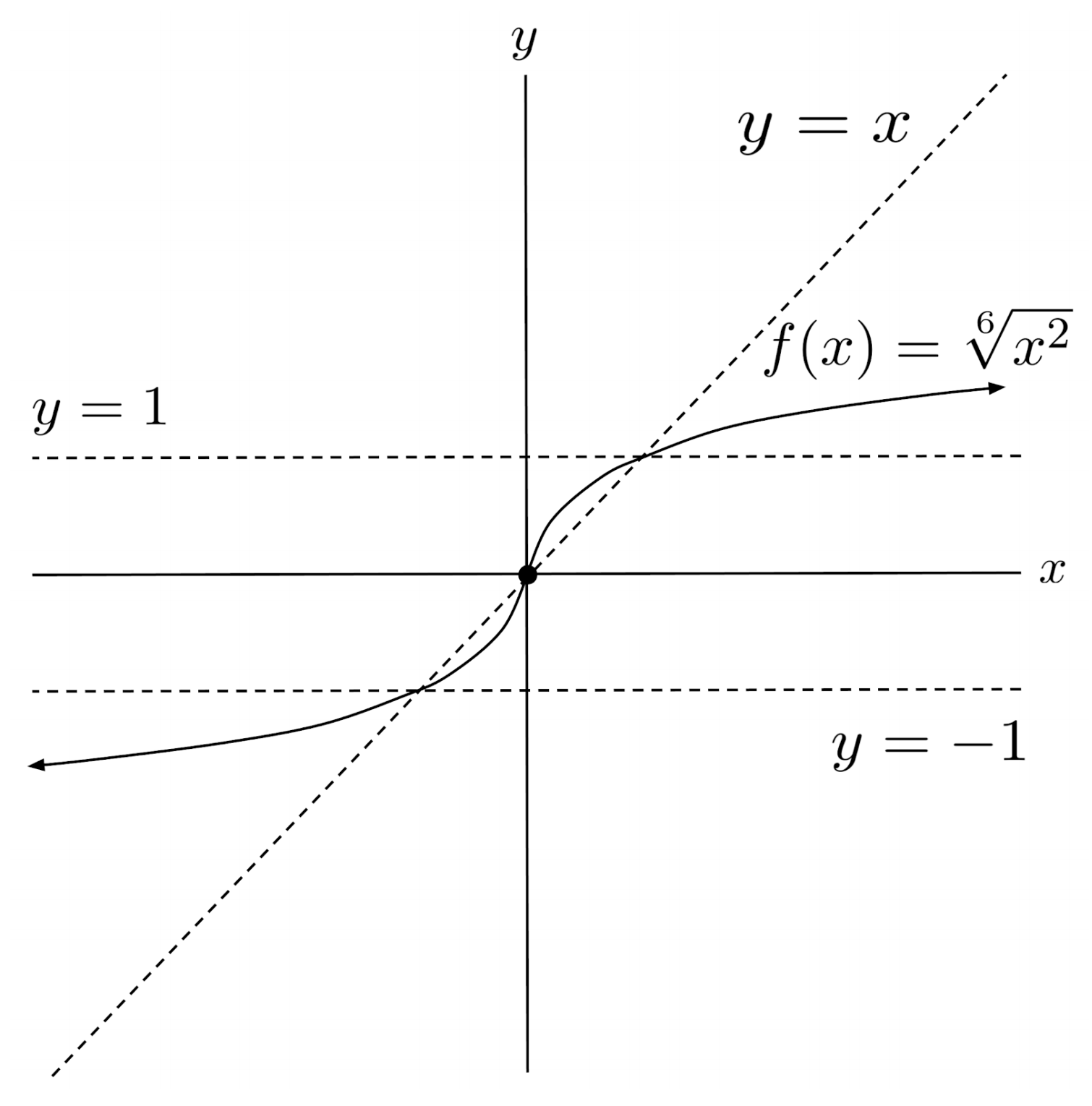
$3) \hspace{.5cm} f(x)=\sqrt[5]{x^3}$

Solution:

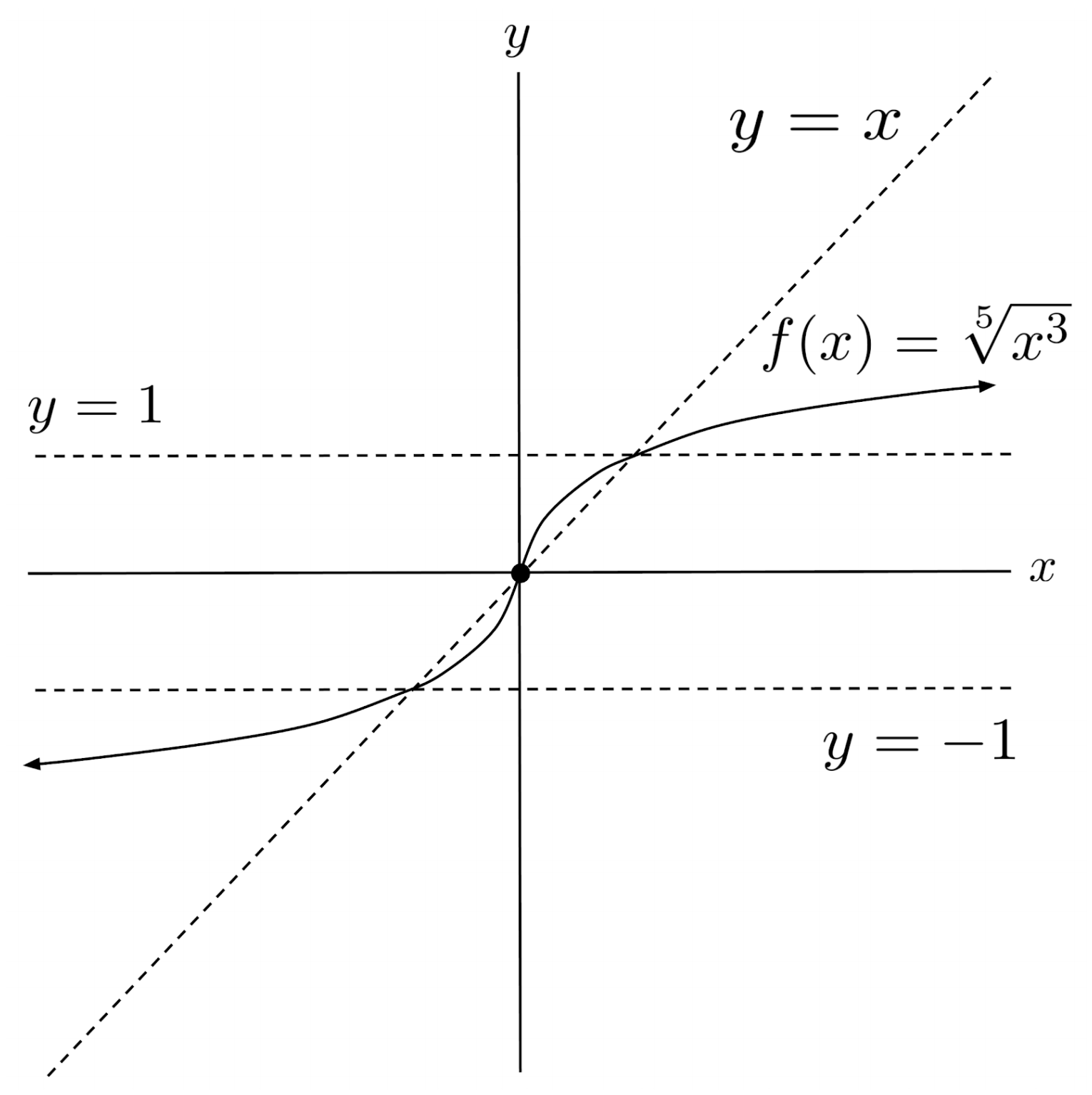
$4) \hspace{.5cm} f(x)=\sqrt[5]{x^4}$

Solution:

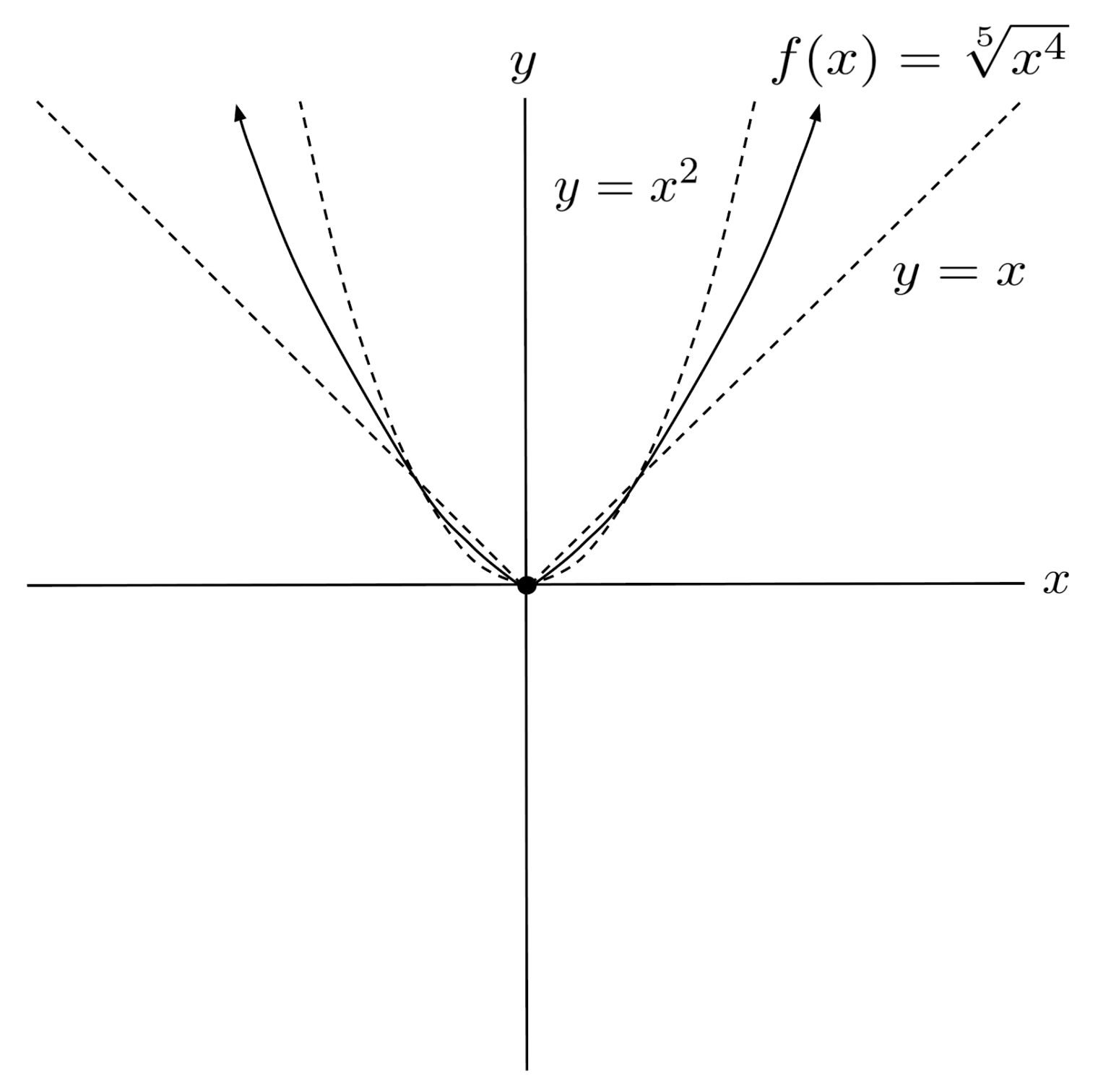
$5) \hspace{.5cm} f(x)=\sqrt[4]{-x^{15} }$

Solution:

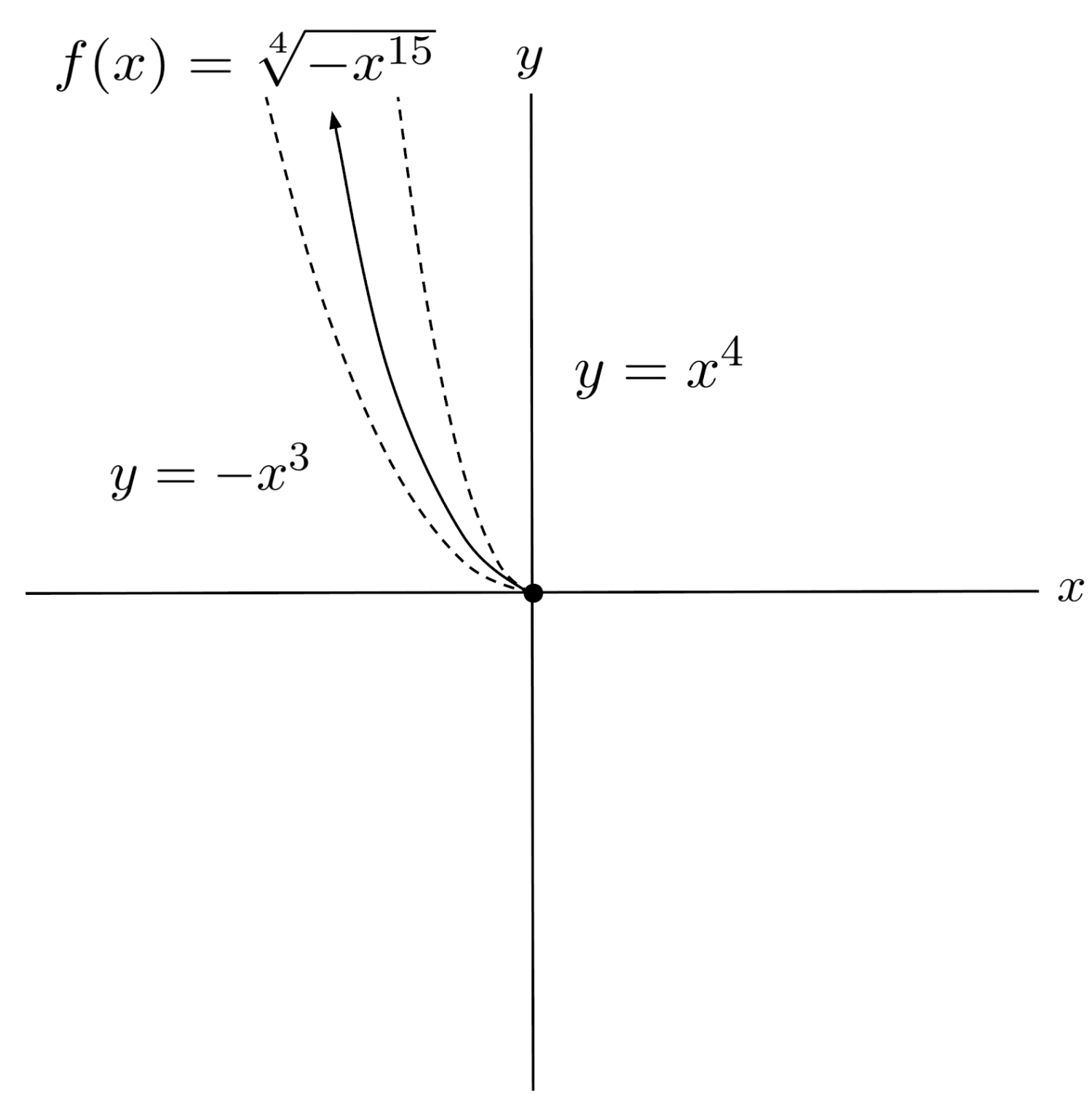
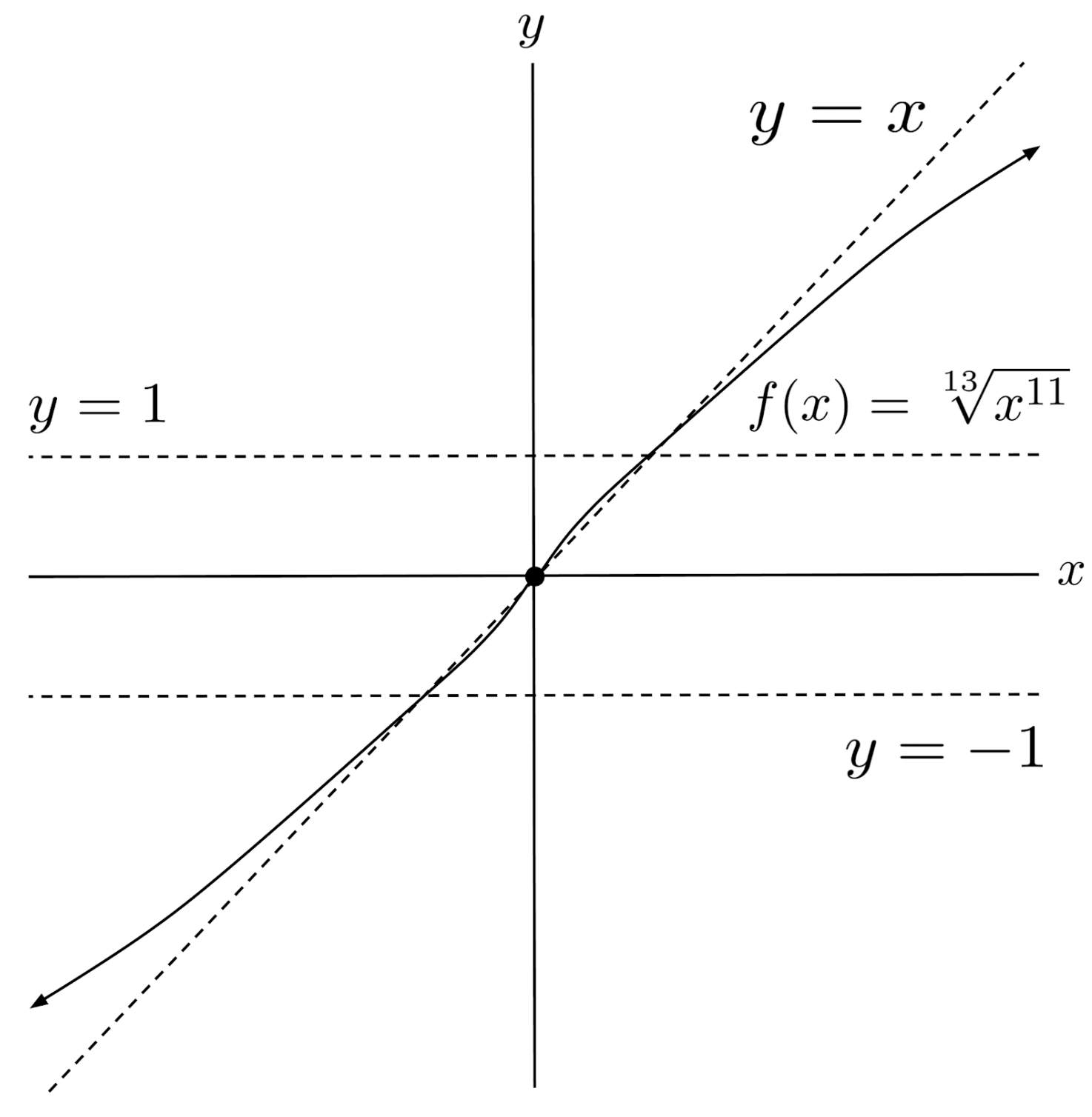
$6) \hspace{.5cm} f(x)=\sqrt[13]{x^{11} }$

Solution:

Solve the following radical functions. (You can view the solution by clicking on the problem.)

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Radical Functions. In Justin Math: Algebra. https://justinmath.com/radical-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.