Linear Inequalities in the Plane

When a linear equation has two variables, the solution covers a section of the coordinate plane.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Linear Inequalities in the Plane. In Justin Math: Algebra. https://justinmath.com/linear-inequalities-in-the-plane/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

When a linear equation has one variable, the solution covers a section of the number line: if our solution is $x > \text{some number}$, then the solution covers the section of the number line that lies right of that number; if our solution is $x<\text{some number}$, then the solution covers the section of the number line that lies left of that number.

If equality is allowed (i.e. $\geq$ or $\leq$), then we use a closed circle to indicate that the circled number is itself a solution; otherwise, if equality is not allowed (i.e. $>$ or $<$), then we use an open circle.

Similarly, when a linear equation has two variables, the solution covers a section of the coordinate plane. If our solution is $y>mx+b$, then the solution covers the section of the coordinate plane that lies above the line $y=mx+b$, whereas if our solution is $y<mx+b$, then the solution covers the section of the coordinate plane that lies below the line $y=mx+b$.

If equality is allowed (i.e. $\geq$ or $\leq$), then we use a solid line to indicate that points on the line itself are solutions. Otherwise, if equality is not allowed (i.e. $>$ or $<$), then we use a dotted line.

Worked Example

To illustrate, let’s solve and graph a two-variable linear inequality.

Since equality is not allowed in the solution, we draw a dotted line. Since the solution consists of values of $y$ LESS THAN those on the line, we shade under the line.

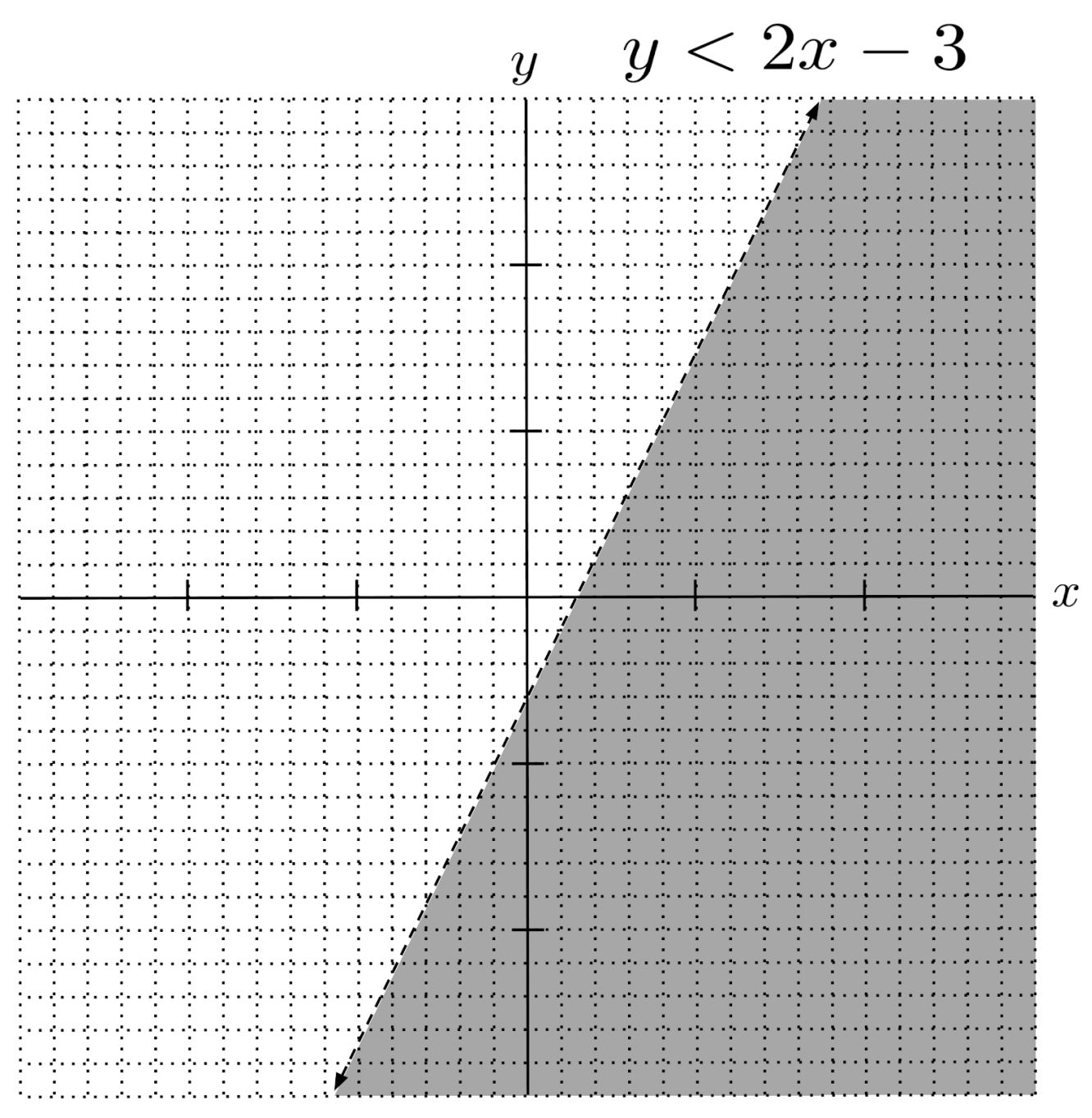
We can check that any point in the shaded region is a solution: for example, substituting $(5,-10)$ into the original inequality yields $3(-10)-5 > 5(-10-5)+6$, which simplifies to $-35>-69$, which is true.

Likewise, we can check that any point NOT in the shaded region is NOT a solution: for example, substituting $(0,0)$ into the original inequality yields $3(0)-0>5(-0-0)+6$, which simplifies to $0>6$, which is not true.

Any point on the line itself will not be a solution, but would be a solution if equality were allowed: for example, substituting the y-intercept $(0,-3)$ into the original inequality yields $3(-3)-0>5(-3-0)+6$, which simplifies to $-9>-9$, which is not a solution but would be a solution if equality were allowed (i.e. $9>-9$).

Case when a Variable Vanishes

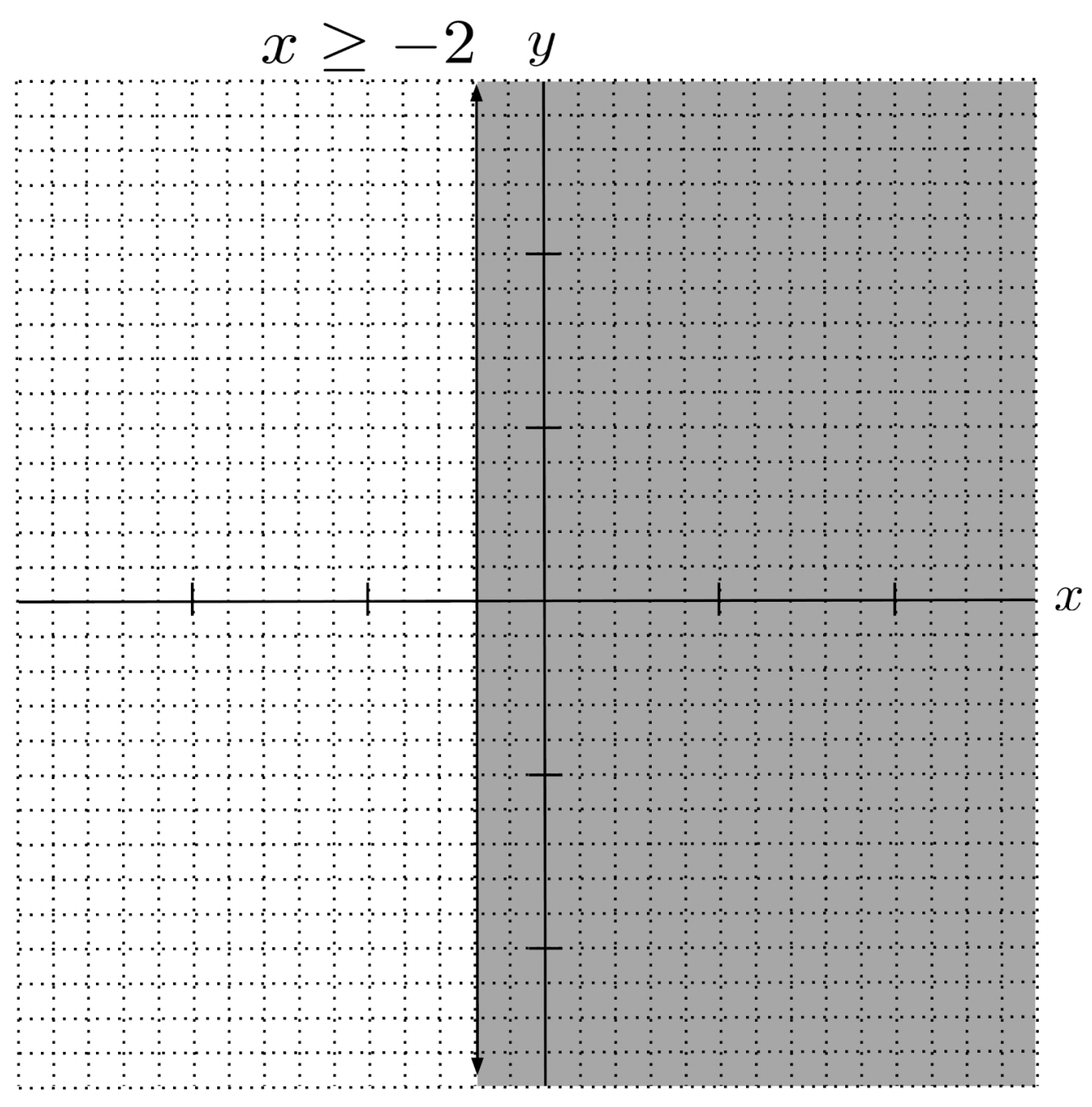
If $y$ vanishes while solving the equation, then the boundary line will be vertical. In this case, we shade left or right of the line depending on whether the solution tells us that $x$ is less than some number, or greater than some number.

Since equality is allowed in the solution, we draw a solid line. Since the solution consists of values of $x$ GREATER THAN those on the line, we shade on the right towards higher values of $x$.

Exercises

Graph the solutions to the inequalities below. (You can view the solution by clicking on the problem.)

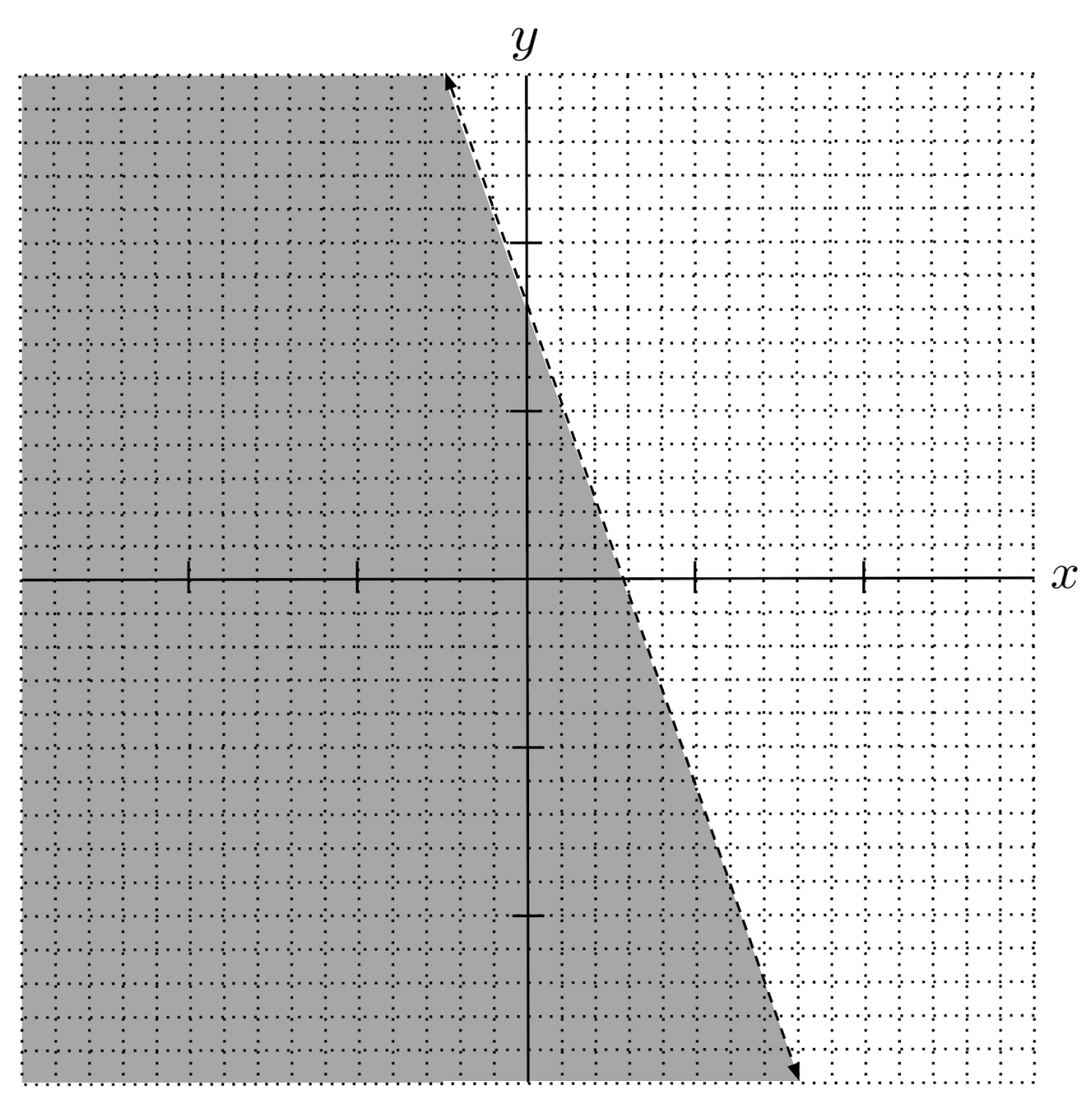
$1) \hspace{.5cm} y < -3x+8$

Solution:

$2) \hspace{.5cm} y \leq \frac{1}{4}x-7$

Solution:

$3) \hspace{.5cm} y \geq 5(x+2)-2$

Solution:

$4) \hspace{.5cm} y < -\frac{3}{8}(x-2) + 3$

Solution:

$5) \hspace{.5cm} 2x+14 \geq 11$

Solution:

$6) \hspace{.5cm} 3x-4y < 12$

Solution:

$7) \hspace{.5cm} y < -5y-7x > 8x-25$

Solution:

$8) \hspace{.5cm} 2(x+3y+2) < x+6y+2$

Solution:

$9) \hspace{.5cm} \frac{1}{4}(x+2y) < \frac{1}{8}(16+2x)$

Solution:

$10) \hspace{.5cm} x > \frac{1}{2}(8y+30)$

Solution:

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Linear Inequalities in the Plane. In Justin Math: Algebra. https://justinmath.com/linear-inequalities-in-the-plane/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.